一种新型三阶磁控忆阻器模型及其滤波器研究

于永斌，李 镖，唐 倩

(电子科技大学信息与软件工程学院 成都610054)

1971年，文献[1]从对称性的角度在理论上预言了忆阻器(memristor)的存在。1976年，文献[2]将忆阻器的概念扩展至忆阻系统(memristive systems)。2008年，文献[3]首次发现了纳米忆阻器件。由此证明了忆阻器的存在，并掀起了忆阻器研究的热潮。忆阻器在非易失性存储器[4]、逻辑门运算[5]、人工神经网络[6]、生物学[7]、忆阻混沌电路及动力学研究[8-10]等多个领域具有丰富的应用前景。

忆阻器描述的是电荷q与磁通量φ 之间的关系[1]，若磁通量 φ是电荷q的单值函数，则忆阻M(q)是电荷q的单值函数，称之为荷控忆阻器。同样地，若电荷q是磁通量φ的单值函数，则忆导W(φ)是磁通量φ的单值函数，则称之为磁控忆阻器(或忆导器)。

根据荷控与磁控忆阻器的定义，两者的特征分别由φ−q曲线或q−φ曲线决定。基于q−φ三次非线性关系，文献中[9]提出了一种三阶磁控忆阻器模型。基于φ−q二次非线性关系，文献[11]提出了一种荷控忆阻器模型。基于q与φ之间分段线性关系，文献[12]提出了荷控和磁控忆阻器模型。

滤波器是一种对不同频率范围内的信号具有不同抑制作用的频率选择电路。由电阻和电容组成的无源滤波是最常见的滤波器，而基于忆阻器的滤波器却比较少见。文献[13]使用HP忆阻器模型搭建了高低通滤波器，并进行了仿真分析；文献[14]基于三阶磁控忆阻器搭建了高低通滤波器，并进行了仿真和实际电路分析；文献[15]基于三阶磁控忆阻器搭建了有源低通滤波器。

本文基于q−φ之间三次多项式关系，提出了一种新型的三阶磁控忆阻器模型。与文献[9-10,14-15]中使用的三阶磁控忆阻器模型不同，本文描述q−φ关系的三次多项式中二次项φ2的系数不为0，模型更具有一般性。同时基于新型三阶磁控忆阻器模型设计了一阶低、高通滤波器。仿真与实际电路分析结果表明：本文设计的新型三阶磁控忆阻器模型具备忆阻器的3个基本特征[16]，即忆阻器两端电压与流经的电流呈"8"字形滞回曲线，随着频率的升高，滞回曲线所包围的面积减小，当频率趋近于无穷时，滞回曲线退化成单值函数。

1 一种新型三阶磁控忆阻器的建模

如前所述，磁控忆阻器中电荷q是磁通量 φ的单值函数，本文将函数q(φ)进行泰勒级数展开，其表达式为：

式中，an为φn的系数。为了简化问题，本文只将该多项式展开到三阶，有：

式中，α、β和γ 分别为各次项的系数，其值均为常数。与文献[9-10,14-15]使用的三阶磁控忆阻器模型相比，本文提出的磁控忆阻器模型在描述q−φ关系时多了 βφ2分量，使之更具有一般性。当β=0时，此时忆阻器模型与文献[9-10,14-15]提出的忆阻器模型一致。

结合W(φ)=dq(φ)/d(φ)，可以得出相应的忆导W(φ)为：

新型三阶磁控忆阻器与无 φ的二次分量的三阶磁控忆阻器的q−φ曲线和W−φ曲线如图1所示，其中α= 1 S，β =1 S/Wb，γ=1 S/Wb2。

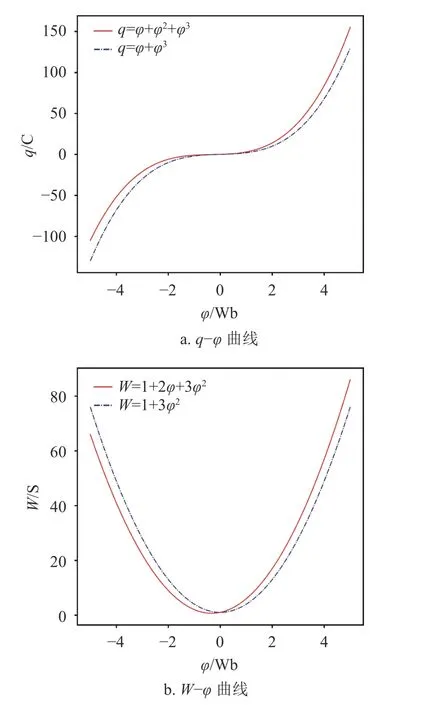
图1 q-φ与W-φ曲线

由电压v、磁通量φ 和时间t三者之间的关系式v(t)=dφ(t)/dt以及电压v、电流i以及电导W三者之间的关系式i(t)=W(φ)v(t)可以得出：

式中，φ0为磁通量的初始量。可以看出，磁控忆阻器的输出不仅跟此刻的输入有关，还与此前的输入有关，体现了忆阻器的“记忆”特性。另外，为了使磁控忆阻器的伏安特性曲线始终在第一、三象限内[11,16]，即忆导值始终大于0，则要求α、β和 γ三者之间的关系为：

为了检验该模型是否正确，本文设置一个电压源输出的电压信号为：

由式(4)与式(6)可得电流i(t)的表达式：

现给定输入电压源，选取幅值A、频率ω，以及参数α、β和γ的值如表1所示。根据式(7)在MATLAB软件中仿真可得该三阶磁控忆阻器的二端电压以及对应的电流波形和伏安特性曲线，如图2所示。

表1 三阶磁控忆阻器模型参数值

从图2b的三阶磁控忆阻器伏安特性曲线可以看出，该滞回曲线在原点相交，位于第一、三象限，且形状呈斜“8”字形，说明该三阶磁控忆阻器模型符合忆阻器的特性。

图2 三阶磁控忆阻器仿真图

2 三阶磁控忆阻器的等效电路

2.1 “浮地”二端口等效电路原理

上一节忆阻器的建模过程中对电压的各种运算都是相对于零电位而言的，如果直接根据式(4)搭建忆阻器等效电路，那么该等效电路的一端必然会接地。

为了克服忆阻器等效电路一端接地的局限性，使之成为“浮地”二端口，文献[17-20]提出了多种浮地忆阻器等效电路，然而其中的电路结构较为复杂。为简化电路，本文将相对于零电位的电压转换为二端口之间的“电位差”[14]，从而得到如下所示的三阶磁控忆阻器的二端口“浮地”表达式：

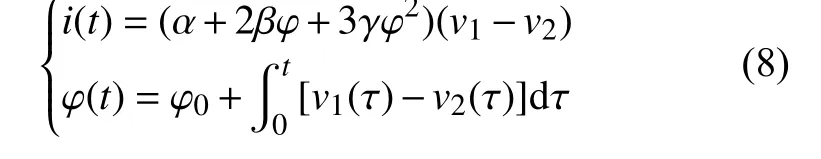
式中，v1和v2分别代表忆阻器等效电路两端的电压。

2.2 三阶磁控忆阻器电路实现

忆阻器等效电路二端口之间的电位差可以利用由运算放大器构成的减法器计算得出。之后便可以将计算得出的电位差进行加法、乘法以及积分运算。具体的电路图实现如图3所示。

该忆阻器等效电路由15个电阻、一个电容、5个AD712运算放大器以及3个AD633乘法器构成，整个等效电路由15 V直流电源驱动。由于本文中所提出的新型三阶磁控忆阻器模型多了 βφ2分量，因此该等效电路中使用乘法器U6来计算该分量。

运算放大器U1A构成一个电压跟随器，它具有高输入阻抗和低输出阻抗的特点，输入电流极少进入运算放大器，起到与前级电路隔离的作用。其输出电压v3等于输入电压v1。

运算放大器U1B与电阻R1～R4构成一个减法器。由于电阻R1～R4的阻值相等，因此输出电压v4与输入电压v2、v3之间的关系为：

运算放大器U2A与电阻R5～R7以及电容C1构成一个积分器。由于实际运算放大器并不是理想的，因此电阻R7的作用是为了减小误差。电阻R6的作用是为了防止积分漂移所造成的积分饱和或截止现象，同时，为了减小积分误差，电阻R6>>R5。输出电压v5与输入电压v4之间的关系为：

U4～U6为AD633乘法器，根据其数据手册知其输入输出之间的关系式为：

图3 三阶磁控忆阻器等效电路图

根据式(11)可以直接计算出电压v6与电压v7的表达式：

运算放大器U2B与电阻R13、R14构成一个反相放大器，由于电阻R13=R14，因此输出电压v8与输入电压v2之间的关系为：

运算放大器U3A与电阻R8～R12构成一个反相加法器。同样地，电阻R12的作用是为了减小计算误差。由于电阻R8～R11的阻值均为10 kΩ，因此输出电压v9与输入电压v6、v7、v8之间的关系为：

最后，根据电阻R15两端的电压即可计算出流经电阻R15的电流。正如前面所提及，几乎没有电流流入运算放大器U1A，因此流经R15的电流即为流经忆阻器的电流。结合式(8)～式(15)，即可得出电流i(t)的表达式为：

2.3 三阶磁控忆阻器电路仿真分析

在Cadence(PSpice)软件上对上述三阶磁控忆阻器的伏安特性进行仿真分析。根据式(5)中α、β和γ 三者之间的关系，并经过一些调优，电阻电容的设置如下：C1=200 nF、R5=10 kΩ、R15=10 kΩ。可以计算出α=0.1 mS、2β=5 mS/Wb、3γ=0.25 S/Wb2。

为了测试三阶磁控忆阻器等效电路的伏安特性，使用如图4所示的测试电路。正弦电源V3的两端接入忆阻器等效电路的MEM_PLUS端和MEM_MINUS端。为了体现该忆阻器等效电路的浮地特性，电压源两端均未接地。同时，在正弦电压源端标记一个电流探针，用以测量经过忆阻器的电流大小，将横坐标改为电压源的幅值便可画出该忆阻器等效电路的伏安特性曲线。

图4 三阶磁控忆阻器等效电路的测试电路

将正弦电压源的幅值固定为5 V，分别设置频率为100、200 Hz、10 kHz，其伏安特性曲线如图5所示。从图5中可以看出，该忆阻器模型符合忆阻器的3个特征[16]：当忆阻器两端施加周期信号时，其伏安特性曲线为滞回曲线，且经过原点；随着频率增加，其滞回曲线面积减小；当频率趋近于无穷时，其滞回曲线退化成为单值函数，忆阻器退化成为线性电阻。

图5 不同频率的伏安特性曲线

将电压源的频率固定为100 Hz，分别设置振幅为3、5、7 V，其伏安特性曲线如图6所示。从图6中可以看出：随着忆阻器等效电路两端电压增加，其滞回曲线所围成的面积也会随之增加。

图6 不同振幅的伏安特性曲线

3 基于新型忆阻器的滤波器

3.1 基于磁控忆阻器的低通滤波器

基于磁控忆阻器(忆导)的WC低通滤波器电路图如图7所示。

图7 基于磁控忆阻器的低通滤波器

根据基尔霍夫定律，流经忆导器W与电容C的电流相等，联立式(8)可以列出：

由于基于磁控忆阻器的低通滤波器为时变系统[14]，不能使用一般的系统传输函数进行分析，因此从定性的角度对该系统进行分析。根据式(7)可以得出，三阶磁控忆阻器在低频信号的驱动下，会产生明显的二次和三次谐波分量。由电容的传输函数HC(jω)=1/jωC可知，频率越高，电容C的阻抗越小。因此，WC低通滤波器相较于RC低通滤波器，在其通带内(即低频信号)的输出增益较低。

基于图3所示的三阶磁控忆阻器(忆导)W，搭建出低通WC滤波器，并在PSpice软件中进行仿真，与此同时，搭建出一个RC低通滤波器进行比较，如图8所示。

图8 WC与RC低通滤波器电路图

图9为WC低通滤波器与RC低通滤波器的仿真结果。从图中可以看出，WC低通滤波器输出增益较RC低通滤波器低，且相位变化也与RC低通滤波器有所不同。表明了磁控忆阻器由于对低频信号产生高次谐波分量，其具有非线性特性。

图9 WC与RC低通滤波器频率响应图

3.2 基于磁控忆阻器的高通滤波器

基于磁控忆阻器(忆导)的9高通滤波器电路图如图10所示。

图10 基于磁控忆阻器的高通滤波器

同样根据基尔霍夫定律，流经忆导器W与电容C的电流相等，联立式(8)可以列出：

根据忆阻器的基本特征：随着频率增加，其滞回曲线面积减小；当频率趋近于无穷时，其滞回曲线退化成为单值函数，忆阻器退化成为线性电阻。因此WC高通滤波器与RC高通滤波器在高频带输出增益几乎一致。

基于图3所示的三阶磁控忆阻器(忆导)W，搭建WC高通滤波器，并在PSpice软件中进行仿真，同时，搭建出一个RC高通滤波器进行比较，如图11所示。

图11 WC与RC高通滤波器

图12为WC高通滤波器与RC高通滤波器的仿真结果。从图中可以看出，WC高通滤波器输出增益与RC高通滤波器输出增益几乎无差异，且两者的输出相位也类似。这表明忆阻器在高频信号的激励下，退化成为线性电阻。

图12 WC与RC高通滤波器频率响应图

4 实际电路分析

三阶磁控忆阻器等效电路的实际电路如图13所示。该实际电路采用AD712JN双通道运算放大器和AD633JN乘法器。另外，为了稳定运算放大器电压源的电压，在正负电压源的输入端并联一个电容以消除干扰。

图13 三阶磁控忆阻器等效电路的实际电路

4.1 三阶磁控忆阻器等效电路伏安特性分析

由于流经忆阻器等效电路的电流与电阻R15两端的电压成正比，因此可以使用减法器计算R15两端的电压从而间接得到流经忆阻器等效电路的电流波形。

将正弦输入信号的电压振幅固定为5 V，频率分别取200、500 Hz以及10 kHz，其三阶磁控忆阻器两端的电压和电流波形以及伏安特性曲线分别如图14a～图14c所示。其中时域波形中黄色代表电压波形，蓝色代表电流波形。

图14 三阶磁控忆阻器的时域波形图及伏安特性曲线

从时域波形中可以看出：在低频信号的激励下，流经忆阻器的电流中存在一定的谐波分量；随着激励信号频率的增加，其电流波形逐渐表现为标准正弦信号，呈线性特性，与理论分析和仿真结果表现一致。

从伏安特性曲线中可以看出：忆阻器的伏安特性曲线在第一、三象限呈斜“8”字形滞回曲线，且在原点自相交；随着频率的增加，滞回曲线围成的区域的面积逐渐减小；当频率趋近于无穷时，滞回曲线退化成为一条直线。

4.2 基于忆阻器的低通滤波器

将WC低通滤波器两端的正弦输入信号的电压振幅固定为5 V，频率分别为100、500、1 000 Hz，其输入与输出电压的时域波形如图15所示。其中黄色代表输入信号电压波形，蓝色代表输出信号电压波形。从图中可以看出，随着输入信号频率的增加，其输出信号的振幅逐渐减小，且相位偏移量也逐渐增加。这与仿真结果表现一致。

图15 基于忆阻器的低通滤波器输入与输出波形

4.3 基于忆阻器的高通滤波器

将WC高通滤波器两端的正弦输入信号的电压振幅固定为5 V，频率分别为100、500、1 000 Hz，其输入与输出电压的时域波形如图16所示。其中黄色代表输入信号电压波形，蓝色代表输出信号电压波形。从图中可以看出，随着输入信号频率的增加，其输出信号的振幅逐渐增加，且相位偏移量逐渐趋近于0。这与仿真结果表现一致。

图16 基于忆阻器的高通滤波器输入与输出波形

5 结束语

本文提出一个新的三次非线性多项式来描述电荷与磁通量之间的关系，再对忆阻器进行建模，并验证了该模型的可行性。随后基于该模型使用模拟运算电路搭建出一个三阶磁控忆阻器等效电路。理论分析、基于PSpice的仿真以及实际电路结果都表明：该三阶磁控忆阻器符合忆阻器的3个基本特征，在低频信号激励下呈非线性特征，在高频信号激励下呈线性特征。之后使用该三阶磁控忆阻器搭建出了低通与高通滤波器，并与基于电阻的RC滤波器进行了比较。实验与仿真结果表明：由于忆阻器在低频信号下的非线性特性，基于新型三阶磁控忆阻器的低通滤波器RC低通滤波器输出增益低；由于忆阻器在高频信号下的线性特性，基于新型三阶磁控忆阻器的高通滤波器较RC高通滤波器输出增益基本一致。