高速转子—支承结构系统动力学的缩尺相似设计方法研究

王立 梁昊天 周标 臧朝平

高速转子—支承结构系统动力学的缩尺相似设计方法研究

王立1梁昊天2周标2臧朝平2

（1 中国航发湖南动力机械研究所，株洲 412002；2 南京航空航天大学能源与动力学院，南京 210016）

基于相似理论提出了一种高速转子—支承结构系统动力学的缩尺相似设计方法。以某型涡轴发动机燃气发生器转子—支承系统总体结构为研究对象，考虑结构的动力学特性相似，建立了几何尺寸参数、支承刚度的缩尺比例，使缩尺后的转子—支承系统与全尺寸的原型相比，具有临界转速成比例、转子振型保持一致的动力学特性；随后，基于该缩尺模型，指导了供实验室使用的航空发动机整机试验器转子—支承系统的结构设计；最后，建立了整机试验器转子—支承系统的“超模型”并进行仿真计算，结果验证了该相似设计方法的合理性和有效性。

缩尺模型；相似理论；高速转子—支承系统；转子动力学

0 引言

转子—支承系统是高速旋转机械如航空发动机、燃气轮机的核心部件，直接影响了设备运行的安全性和稳定性，其动力学问题一直得到国内外学者广泛关注。原型试验是研究高速转子—支承系统动力学特性的重要手段之一，然而，由于原型测试耗时、搭建原型试验系统成本巨大，设计开发缩尺模型以代替原型的测试与仿真，仍是一种低成本、高效的设计与研究方法。

缩尺模型是指能够模拟大尺寸原型的小尺寸样件。高速转子—支承系统动力学缩尺相似设计的理论依据是相似理论，相似理论是阐明自然界和工程中各种相似现象的内在机理的学说[1]，通过相似理论可推导出缩尺模型与原型相似的必要条件。Rayleigh[2]首次利用相似理论中的量纲分析法指导缩尺建模，而量纲分析法至今仍为获得相似条件的重要方法。

相似理论在振动、冲击等领域得到广泛应用。Balawi[3]等人利用系统方程推导了低速冲击载荷下周向固支盘的相似条件，并建立了盘的缩尺模型。Morton[4]利用量纲分析法推导了冲击载荷下的碳纤维复合材料梁的相似条件。Luo[5]等人针对带齿形密封环的薄壁圆柱壳体进行了动力学相似设计。Torkamani[6]基于相似理论推导了正交加强筋圆柱壳自由振动的相似条件。Rosa[7]利用缩尺金属板预测了原型金属板的振动响应，通过原型与缩尺模型振动能量等效的方法获取相似条件。钱德玲[8]等人设计了可模拟真实高层建筑地震响应的缩尺试验台。NASA曾在20世纪50年代利用缩尺模型研究运载火箭（如土星I号、土星V号、泰坦III号等）的动力学问题[9]。

针对旋转机械的转子—支承系统，缩尺试验器常用于研究全尺寸原型的动力学特性。Wu[10]建立了完全几何相似的转子—支承系统模型，用于预测全尺寸原型的横向振动特性。Bax[11]等人设计了一种几何不相似的汽轮机转子的缩尺模型，使其临界转速与原型相同。Young[12]设计了一种几何完全相似的船用转子的缩尺模型，为确保原型与缩尺模型的激励频率与固有频率的比值相同，其长度方向的尺寸比与其径向方向尺寸比相一致。丁一[13]归纳总结了变态相似理论，推导了转子系统变态模型与原型的相似准则，对实际发动机燃气发生器和动力涡轮转子系统进行了动力学相似设计。侯理臻[14]根据相似理论设计了包含叶片飞脱装置的不平衡试验系统，以研究大涵道比涡扇发动机叶片飞脱时的动力学响应。

高转速转子—支承系统通常结构复杂，缩尺模型设计时，如果采用完全几何相似设计，有可能会导致缩尺转子—支承系统的制造困难，并引入一些实际问题。如几何缩尺后的部件可能存在一定的强度削弱问题，同时几何尺寸成比例地降低会导致系统固有频率和临界转速的升高，使得驱动端功率增大，并且需要在极高转速处进行动平衡，增加了试验器调试、测试难度与系统运行的危险性。因此，高速转子—支承系统动力学缩尺相似设计，需要考虑一定的几何畸变。Luo[5]在设计带齿形密封环的薄壁圆柱壳体动力学相似试验件时，考虑了一定的几何畸变，以得到等效圆柱壳体。Oshiro[15]利用几何畸变的模型，准确地预测了全尺寸原型在冲击载荷下的力学行为。然而，上述研究只针对薄壁壳体等简单结构进行了几何畸变相似设计，高速转子—支承系统几何畸变相似设计的研究仍然较少。

本文提出了一种针对高速转子—支承系统的动力学缩尺相似设计方法，用于指导有限试验条件下使用的航空发动机整机试验器转子—支承系统的设计。该动力学缩尺相似设计方法不但考虑了结构简化（几何畸变），且满足动力学相似，即较低的工作转速内使其频率和临界转速成比例降低，同时振型保持不变。最终得到的缩尺转子—支承系统可完全满足实验室使用条件。

1 高速转子—支承系统动力学缩尺相似设计

开展高速转子—支承系统缩尺动力学相似设计前，应首先明确全尺寸原型的结构和动力学特性。图1为某型涡轴发动机燃气发生器转子—支承系统总体结构，总长约0.65m；压气机由5级轴流式和1级离心式构成；涡轮由2级轴流式涡轮构成；其工作转速范围为30000～45000转每分钟；转子支承在两个鼠笼式弹性支承上；两端设计有挤压油膜阻尼器。该燃气发生器转子为高速柔性转子，工作转速内越过前三阶临界转速，前三阶临界转速分别为5563rpm、7604rpm和28243rpm，前两阶模态为刚体模态，第三阶模态为弯曲振型（见图2）。

图1 某型涡轴发动机燃气发生器转子—支承系统原型

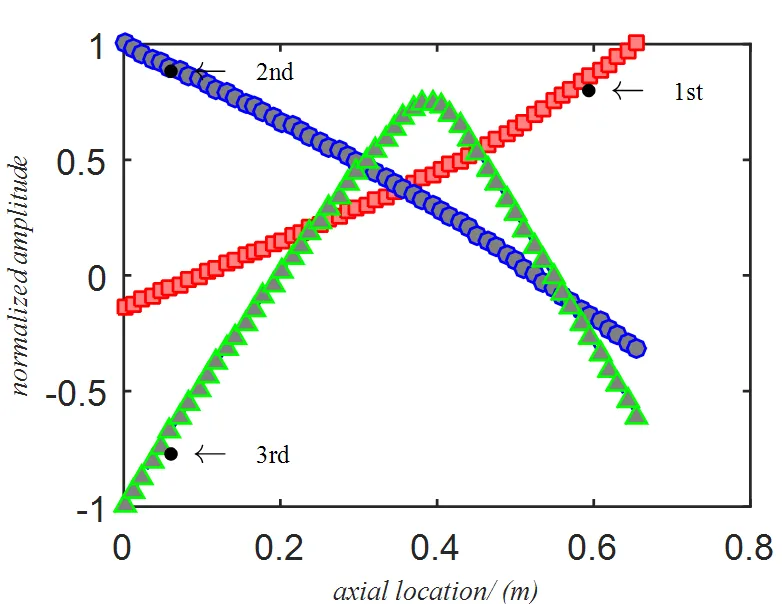
图2 全尺寸原型前三阶振型

缩尺转子—支承系统应能够充分反映全尺寸原型的动力学特性，即前三阶临界转速与全尺寸原型成比例，振型相似。考虑到实验室环境和条件、操作和控制的安全性，拟将缩尺转子—支承系统的工作转速降至10000rpm以内。因此提出转子—支承系统的动力学相似设计目标如下：1）缩尺转子—支承系统工作转速内包含三阶临界转速，前三阶频率和临界转速为全尺寸原型的1/4；2）转子前三阶振型应与全尺寸原型保持一致。

为保证动力学相似，缩尺转子—支承系统应与全尺寸原型具有相同的支承形式，即采用相同形式的滚动轴承，鼠笼式弹性支承并设计有挤压油膜阻尼器。此外，应对缩尺模型进行适当的结构简化，有利于制造和组装。

2 高速转子—支承系统动力学缩尺相似设计

为实现设计目标，本文采用了一种分步缩尺动力学相似设计的策略。该策略是源于Miao[16]设计的双转子系统的缩尺动力学相似试验件。首先对全尺寸原型（Full-scale Prototype，简写为FSP）进行结构简化，得到动力学等效模型（Dynamically Equivalent Model，简写为DEM），然后由动力学等效模型得到动力学缩尺模型（Reduce Scale Model，简写为RSM）的参数（几何、支承刚度等）缩放比例。该策略如图3所示。

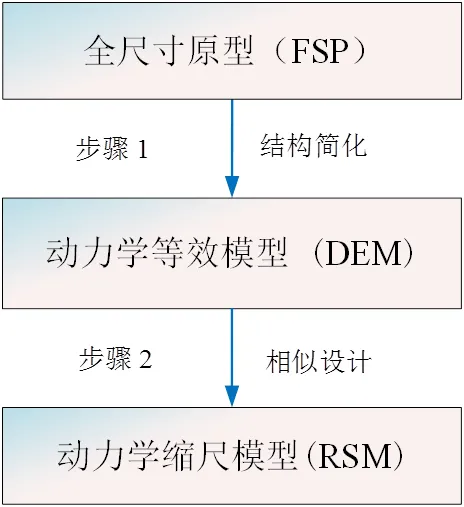
图3 缩尺动力学相似设计策略流程图

2.1 全尺寸原型的结构简化

全尺寸原型的结构简化应保证结构简化后的动力学等效模型，其动力学特性（频率、振型、临界转速）应与全尺寸原型一致。动力学等效模型可以避免在随后的试验件加工制造时，由于几何结构的复杂性带来的高昂的成本，并大大减少后续相似设计的复杂性。简化的过程为：减少盘的数目，将多级压气机、涡轮简化为单盘或双盘，将非均匀截面轴简化为均匀截面轴。此结构简化方式会导致一定的几何畸变。此外，结构简化时应注意：1）支承位置应与全尺寸原型保持一致；2）轴向刚度、质量分布与全尺寸原型相同。

2.2 转子—支承系统的动力学相似设计方法

动力学相似设计是基于相似理论建立动力学等效模型与动力学缩尺模型的相似条件，推导几何尺寸、支承刚度等参数的缩放比例。相似条件可通过量纲分析法与转子动力学控制方程相结合的方式获得。

图4 简单圆截面转子示意图

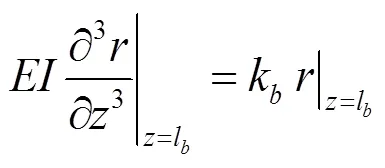
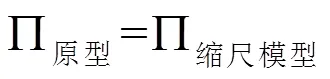
而Π关系式可以通过方程分析与边界条件推导得出。由式（1）、（2）可知，除横向位移（因变量）外，系统存在8个独立变量（见表1），取质量—长度—时间为基本量纲，则独立的Π关系式共有5个。

表1 转子—支承系统独立物理量

将式（4）代入式（1）、（2）中，得到相似模型的运动方程及边界条件为

为保证相似前后微分方程及边界条件的一致性，式（5）、（6）中各项系数应满足如下关系。

将式（4）代入式（7）、（8）、（9），得到一组Π关系式

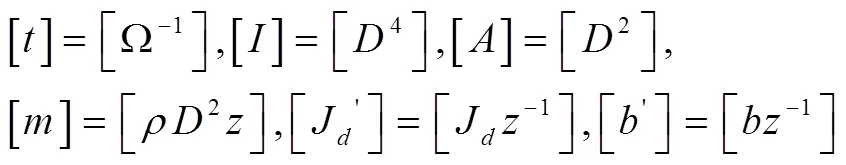
表2 转子—支承系统各主要物理量相似比

3 高速转子—支承系统动力学相似设计

针对前文中的某型涡轴发动机燃气发生器转子—支承系统，按照第2节所述的动力学相似设计策略，开展缩尺动力学相似设计。

3.1 基于全尺寸原型的动力学等效模型

对全尺寸原型进行结构简化，建立动力学等效模型，如图5所示。

动力学等效模型由一根均匀圆截面实心轴和三级盘构成，5级轴流式压气机简化为盘1，离心式压气机简化为盘2，2级轴流式涡轮简化为盘3。盘为均质圆盘，简化了全尺寸原型的部分复杂几何结构特征（如叶片、复杂几何形面等）。动力学等效模型的盘与轴的材料为钢。尽可能地保证动力学等效模型与全尺寸原型相同的轴向刚度、质量分布及支承位置。

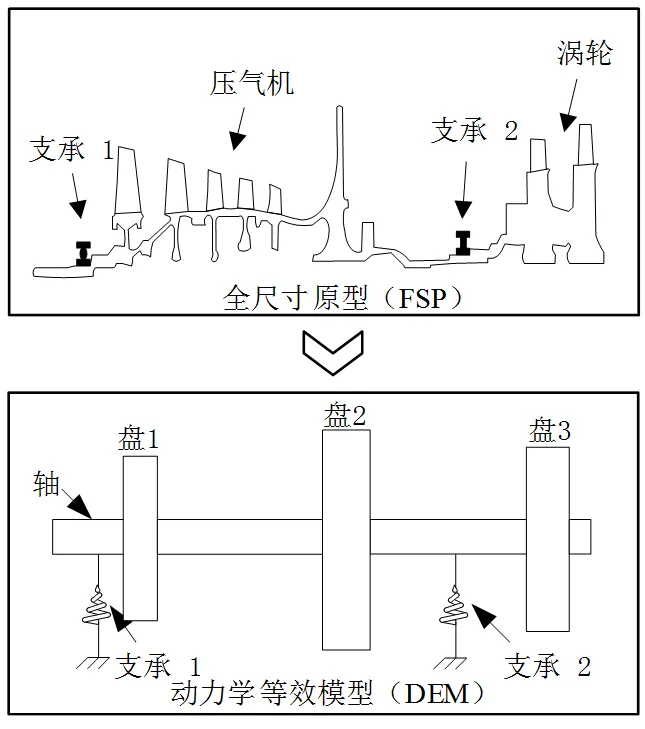
图5 动力学等效模型示意图

3.2 基于动力学等效模型的动力学畸变模型

基于结构简化的动力学等效模型开展相似设计，但严格按照该方法进行动力学相似设计可能导致实际构件设计和制造困难。根据表2，在材料参数保持不变的情况下，频率和临界转速的相似比与转子直径和长度满足如下关系

即频率或临界转速的相似比与直径的相似比成正比，与转子长度的相似比的平方成反比。因此与可通过减小转子直径或增长转子长度以达到成比例降低频率或临界转速的目的。然而，出于缩尺角度的考虑，往往选择减小转子直径同时保证转子长度不变，即

这将会引发实际问题。根据表2，在保证材料参数、轴长不变的情况下，支承刚度的相似比和转子直径的相似比满足如下关系：

即支承刚度的相似比与转子直径相似比的四次方成正比。根据第1节所述的动力学相似设计目标，如果严格按照1/4的比例降低临界转速，根据式（16）、（17）可得

根据式（18）计算支承刚度的相似比

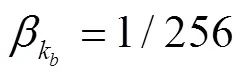
若支承刚度按照1/256的比例降低，这将会导致极低的支承刚度（支承1相似后的支承刚度为1.52×104N/m，支承2相似后的支承刚度为2.15×104N/m）。该支承刚度将会导致动力学缩尺模型所采用的鼠笼式弹性支承设计（一种弹性支承的设计形式（见图6）加工困难。针对上述问题，本文提出一种解决方案，即在动力学等效模型的基础上，引入动力学畸变模型（Dynamically Distorted Model，简写为DDM），如图7所示。

图6 鼠笼式弹性支承示意图

图7 动力学畸变模型示意图

所谓“动力学畸变模型”是在转子—支承系统动力学等效模型的基础上，保持轴长、支承刚度与支承位置不变，优化动力学等效模型的个别参数（例如轴径、盘径、盘厚等），使其频率、临界转速降低为动力学等效模型的1/2，同时振型保持不变。然后基于动力学畸变模型按照频率比为1/2的比例进行相似设计以获得动力学缩尺模型。因此根据式（16）、（17）得到动力学畸变模型与动力学缩尺模型频率与直径的相似比

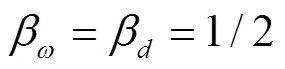
则根据式（18），动力学畸变模型与动力学缩尺模型支承刚度的相似比为

因此最终获得的动力学缩尺模型的支承刚度为全尺寸原型的1/16（支承1相似后的支承刚度为2.46×105N/m，支承2相似后的支承刚度为3.64×105N/m），而该刚度值对于鼠笼式弹性支承设计与加工较为合理。获得动力学畸变模型的问题可以描述为由目标函数和约束条件组成的优化问题，目标函数、约束条件为如下形式。

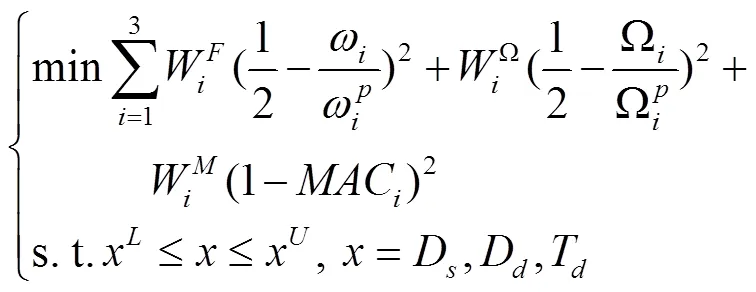
图8 转子—支承系统动力学畸变模型的有限元模型

表3 动力学畸变模型与全尺寸原型模态参数对比

3.3 基于动力学畸变模型的缩尺相似模型

建立动力学缩尺模型的有限元模型（见图10），并计算前三阶频率及临界转速。图11为动力学缩尺模型的Campbell图，表4为动力学缩尺模型前三阶频率及MAC值。与动力学畸变模型对比，动力学缩尺模型的频率基本按1/2降低，且前三阶振型相关性较好。

与全尺寸原型对比（见表5），动力学缩尺模型的前三阶临界转速基本按1/4降低，且振型相关性较好。其中，第3阶MAC值为0.960，低于前两阶MAC值，第三阶临界转速比为1/3.84，与相似设计目标的1/4存在一定的误差。该误差是由动力学畸变模型引入，因动力学畸变模型是由动力学等效模型经参数优化而来，使用优化工具计算难免会引入误差，因此并不能保证动力学畸变模型的前三阶频率和临界转速与全尺寸原型相比严格按照1/2降低，从而无法使动力学缩尺模型的频率及临界转速与全尺寸原型相比严格按照1/4的比例降低。虽然该缺陷导致前三阶临界转速没有严格按照1/4的比例降低，但大体仍然满足动力学相似设计目标，该误差是可以接受的。

图9 动力学缩尺模型示意图

图10 动力学缩尺模型的有限元模型

图11 动力学缩尺模型的Campbell图

表4 缩尺模型与畸变模型模态参数对比

表5 动力学缩尺模型与全尺寸原型对比

4 缩尺转子—支承系统的结构与效果评估

在高速转子—支承系统动力学缩尺模型的基础上，进一步开展结构设计，并基于超模型开展动力学相似效果评估以验证是否满足设计目标。

4.1 缩尺转子—支承系统结构设计

基于相似理论初步设计的缩尺转子—支承系统，需针对试验条件进行结构设计，例如：考虑轴承安装位置、盘轴连接形式、弹性支承结构等等。完成结构设计的转子—支承系统如图12所示，盘轴之间采用胀紧套连接；盘上加装平衡配重安装孔。转子支承在鼠笼式弹性支承上，鼠笼的支承刚度按照第3节转子—支承系统动力学缩尺模型的支承刚度值进行设计。前后支点分别采用深沟球轴承和圆柱滚子轴承。转子—支承系统通过鼠笼安装边与机匣系统相连。

图12 缩尺转子—支承系统结构简图

4.2 缩尺转子—支承系统“超模型”的建立

在设计初期阶段，建立零组件的“超模型（Supermodel）”以替代实际样机应用于实际航空发动机的结构设计中[18]。“超模型”是指非常细化的三维实体有限元模型，在建模过程中保持模型的几何特征与实际结构一致，且网格密度足够大，既消除了模型简化误差，也最大限度降低了有限元网格划分的离散误差，能够足够精确地反映结构的动力学特性。关于“超模型”的建模过程详情可参阅参考文献[18]。

首先依次建立转子—支承系统中的转子组件、鼠笼结构的“超模型”，然后将各子结构的“超模型”装配后，构成转子—支承系统组件的“超模型”。这里需要特别指出的是：1）由于盘轴采用胀紧套连接，近似的将盘轴按刚性连接处理；2）忽略盘轴系统的局部特征，例如盘上的不平衡配重安装孔；3）轴承采用弹簧单元建模，其径向刚度为108N/m（由轴承制造商提供）；4）鼠笼安装边处固支以模拟转子—支承系统装机状态（见图13）。

图13 缩尺转子—支承系统超模型示意图

4.3 动力学相似效果评估

计算缩尺转子—支承系统超模型前三阶临界转速，并与全尺寸原型振型进行相关性分析（见表6）。与全尺寸原型相比，缩尺转子—支承系统超模型前三阶临界转速基本按1/4的比例降低，其振型基本与全尺寸原型基本一致，从而验证了本文提出的针对高速转子—支承系统的缩尺动力学相似设计方法的有效性。

图14 缩尺转子—支承系统超模型的Campbell图

表6 缩尺转子—支承系统超模型的临界转速与MAC

5 结论

本文提出了一种针对高速转子—支承系统的动力学缩尺相似设计方法。应用该方法建立了某型涡轴发动机燃气发生器转子—支承系统的缩尺动力学相似模型，使其临界转速相较于全尺寸原型基本按1/4的比例降低，并保持了振型的相似性。同时，通过动力学相似理论与优化工具的综合运用，有效解决了动力学相似设计需求与几何、结构参数不完全相似的矛盾，规避了部分结构参数（如支承刚度）不合理的现象。最后，进一步进行了缩尺转子—支承系统的结构设计，并建立“超模型”验证了相似设计的合理性和有效性。

[1] 徐挺. 相似理论与模型试验[M]. 北京: 中国农业机械出版社, 1982.

[2] Coutinho, Cristiano P, Baptista, António J, et al. Reduced scale models based on similitude theory: A review up to 2015[J]. Engineering Structures, 2016, 119: 81-94.

[3] Balawi S, Shahid O, Mulla M A. Similitude and scaling laws static and dynamic behavior beams and plates[J]. Procedia Engineering, 2015, 114: 330-337.

[4] Morton J. Scaling of impact-loaded carbon-fiber composites [J]. AIAA journal, 1988, 26(8): 989-994.

[5] Luo Z, Zhu Y, Han Q, et al. The dynamic similitude design of a thin-wall cylindrical shell with sealing teeth and its geometrically distorted model[J]. Advances in Mechanical Engineering (Sage Publications Inc.), 2015, 7(2): 708902-708902.

[6] Torkamani S, Navazi H M, Jafari A A, et al. Structural similitude in free vibration of orthogonally stiffened cylindrical shells [J]. Thin-Walled Structures, 2009, 47(11): 1316-1330.

[7] De Rosa S, Franco F, Polito T. Structural similitude for the dynamic response of plates and assemblies of plates [J]. Mechanical systems and signal processing, 2011, 25(3): 969-980.

[8] 钱德玲, 李元鹏, 刘杰. 高层建筑结构振动台模型试验与原型对比的研究[J]. 振动工程学报, 2013, 3: 138-144. [QIAN Deling, LI Yuanpeng, LIU Jie. Contrast study of shaking table model test with prototype for high-rise building structures [J]. Journal of Vibration Engineering, 2013, 3: 138-144.]

[9] Lucas G Horta, Raymond G Kvaternik. A historical perspective on dynamics testing at the Langley research center[R]. NASA/TM- 2000-210295.

[10] Wu J J. Prediction of lateral vibration characteristics of a full-size rotor-bearing system by using those of its scale models[J]. Finite Elements in Analysis and Design, 2007, 43(10): 803-816.

[11] Baxi C B, Telengator A, Razvi J . Rotor scale model tests for power conversion unit of GT-MHR[J]. Nuclear Engineering and Design, 2011, 251: 344-348.

[12] Young Y L. Dynamic hydro elastic scaling of self-adaptive composite marine rotors [J]. Composite Structures, 2010, 92(1): 97-106.

[13] 丁一, 罗贵火, 王飞. 某双转子发动机变态相似模型设计与验证分析[J]. 重庆理工大学学报(自然科学), 2018, 32(6): 52-58. [DING Yi, LUO Guihuo, WANG Fei. Design and verification analysis of one dual-rotor engine abnormal similar test model[J]. Journal of Chongqing University of Technology (Natural Science) , 2018, 32(6): 52-58.]

[14] 侯理臻, 廖明夫, 王卫国, 等. 叶片飞脱下转子动力学响应实验[J].航空动力学报, 2019, 34(5): 57-66. [HOU Lizhen, LIAO Mingfu, WANG Weiguo, et al. Experiment of rotor dynamics under fan blade-off[J]. Journal of Aerospace Power, 2019, 34(5): 57-66.]

[15] Oshiro R E, Alves M. Predicting the behavior of structures under impact loads using geometrically distorted scaled models[J]. Journal of the Mechanics and Physics of Solids, 2012, 60(7): 1330-1349.

[16] Miao H, Zang C, Friswell, M I. Dynamic similarity design method for an aero-engine dual-rotor test rig[J]. Journal of Physics: Conference Series, 2016, 744: 012109.

[17] 《航空发动机设计手册》总编委会. 航空发动机设计手册第19册: 转子动力学及整机振动[M]. 北京: 航空工业出版社, 2000.

[18] Zang C, Ewins D J. Model validation for structural dynamics in the aero-engine design process [J]. Frontiers in Energy, 2009, 3(4): 480-488.

Reduced-Scale Model Design for a High-Speed Rotor-Bearing System

WANG Li1LIANG Hao-tian2ZHOU Biao2ZANG Chao-ping2

（1 AECC Hunan Aviation Power plant Research Institute, Zhuzhou 412002, China; 2 College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China）

This paper is devoted to developing a similitude design method for reduced-scale model based on similitude theory from a high-speed rotor system prototype. A gas generator for the turboshaft engine is considered as the full-scale prototype, the scaling factors between prototype and relating the critical design parameters such as rotor geometry, support stiffness, etc. are derived; dynamic similitude is assured by proportionally scaling down the three critical speeds while the rotor mode shapes still maintain high correlation between the prototype and downscaled model. The resultant reduced-scale model of the rotor system will practically guide the construction of the essential part of a whole engine dynamics test rig for laboratory use.

Reduced-scale model; similitude theory; high-speed rotor-bearing system; rotor dynamics

V415

A

1006-3919(2021)02-0022-09

10.19447/j.cnki.11-1773/v.2021.02.004

2021-01-08；

2021-03-14

国家自然科学基金(No. 12072146)

王立（1983—），男，高级工程师，研究方向：航空发动机总体结构；（412002）中国航发湖南动力机械研究所.