社会网络下更新产品扩散的投放时机和种子优化

翁克瑞,周 静

(中国地质大学 经济管理学院,武汉 430074)

近年来,面对快速的需求变化和技术更新,许多企业加速产品更新升级换代。在这一背景下,决策者需要从企业和产品生命周期角度考虑更新产品的发布和投放时间,以寻求全生命周期的产品利润最大化。研究显示,推迟上市的策略可以使厂商获得更高的利润和市场效果[1-2]。推迟上市的一个重要原因是避免挤压旧产品的市场空间和利润,同时在旧产品的口碑效应带动下更好地促进新产品的市场渗透。许多企业运用了延期投放策略,例如苹果公司大部分iPhone发布和发售的间隔不超过10天,而iPhone X的间隔时间有52天,美国市场调查机构Slice Intelligence的数据显示,iPhone X预订量是iPhone 6的1.25倍,延期投放使得苹果X 预定数量和利润增加。此外,丰田汽车也多次在中国市场延期推出已经发布的新款汽车,以保证旧产品的利润空间。由此可见,更新产品、技术等通过社会网络进行扩散时,寻找合适的市场对象和投放时机已成为社交商务的一个重要研究方向。

现有学者研究的产品扩散模型基本分为宏观扩散模型和微观扩散模型。宏观扩散从创新扩散的总体水平上对扩散现象进行描述,以Bass[3]模型为代表。针对Bass 模型仅考虑单一产品扩散问题,Norton等[4]提出一个经典的多代更新高科技或耐用产品的生命过程销售模型。宏观扩散模型忽略了用户的异质性,没有考虑具体的网络结构。从微观角度研究并建立微观模型这一概念早有学者提出,Oren等[5]将消费者的某种异质性引入到消费者个体采用决策模型中,并在此基础上构建了一个新产品市场扩散模型。随后,微观扩散模型不断发展,有渗流模型[6]、元胞自动机模型[7]、多Agent模型[8]、复杂网络仿真模型[9]以及临界值模型[10]等。现实中的世界网络具有小世界和无标度特征,周琦萍等[9]和吴靖[11]指出,在社会网络中选择高度数节点作为种子可以促进扩散。李丹丹等[12]证明了控制群体影响力较大的节点能有效控制舆论传播。相比宏观模型,考虑社会网络结构的微观模型更真实地反映产品扩散的动态变化。

现有文献中关于产品扩散的投放时间研究很少,主要有：Su等[13]建立了一个博弈论模型来研究新产品在竞争条件下的发布时间；许博等[14]认为厂商将产品投入市场时要考虑到所面临的市场环境和成本因素；Shocker等[15]指出相对于单个产品的扩散,多代产品的扩散没有得到足够的重视；全雄文等[16]通过Bass销售模型,建立了企业利润模型,对更新产品投放市场时机的相关影响因素做了数值分析,认为更新产品投放时机与潜在市场用户、产品利润以及产品生命周期有关；龚田华等[17]通过运用最优控制理论、扩散理论和方法建立了相关的扩散数学模型,分析了更新换代产品投放时机和动态定价。然而,上述关于更新产品投放时机的研究仍然基于用户的同质性假定,没有考虑社会网络结构,也没有考虑种子选择问题。

更新产品、技术等在社会网络扩散的投放时机和种子优化决策可看作是在一个已存在旧产品的社会网络G(N,E)中,产品以扩散模型P的形式传播其影响力,但新产品投放时旧产品停止扩散,选择投放阶段t和p个新产品种子新旧产品利润之和最大化。龚田华等[17]提出了两类扩散模型：独立集联模型(Independent Cascade Model,ICM)与线性阈值模型(Linear Threshold Model,LTM),其中新产品扩散通常基于LTM。Kempe等[18]提出了求解种子的贪婪算法,传统贪婪算法由于每次选取新节点加入种子集合时需要模拟扩散过程计算并更新所有候选种子的边际影响力,因此时间复杂度过高。此后研究主要集中在大规模社交网络算法的改进,如惰性计算[19-20]、最短路径[21]、有向无圈图[22]、局部树[23]、局部邻域[24]、度数修正[25]、学习自动机[26]、社团探寻[27-28]、进化算法[29-30]以及随机超图[31]等。然而,这些研究一般基于随机阈值,难以反映消费者的个性特征和社会网络的消费环境；在更新产品的扩散中,扩散模型将面临确定性阈值。因此,本文研究社会网络下更新产品扩散的投放时机和种子优化(Launching Time and Seed Selection Optimization of Updated Product,LTSSOUP)问题：在一个已存在旧产品的社会网络G(N,E)中,如果某节点收到来自已激活邻居(指已购买旧产品和新产品的邻居)的影响力不少于确定阈值则被激活,并影响自己的邻居,当未有新节点时停止扩散,并假定新产品投放时旧产品停止扩散,如何选择投放阶段t和p个新产品的种子使得新旧产品利润之和最大化。考虑更新产品的投放时机后,扩散模型将面临确定阈值和动态种子选择问题,传统贪婪算法无法高效求解,尚不能处理大规模复杂网络(如5 万个节点以上的网络)。

本文建立了社会网络下LTSSOUP问题整数规划模型,模型同时对更新产品的投入种子和投放时间进行优化。对大规模LTSSOUP问题设计了多阶段贪婪算法,该方法避免了重新计算扩散仿真,能够高效率地更新边际影响力并获取最优投放时机。实验显示：相比传统贪婪算法,该算法具有更高的求解效率；相比度数下降法、随机算法,该算法能够得到更好的求解质量。通过在一个真实网络中进行扩散模拟,发现考虑社会网络的种子优化后,更新产品利润小、种子数量少、计划阶段限制大时,延期投放容易使厂商获得更高的利润和市场效果。

1 整数规划模型

在社会网络G(N,E)中,N={1,2,…,n}为所有节点的集合,E为边的集合。假定扩散阶段为0→T1→T2,其中,T2为已知的最大扩散时间(假定的产品计划期限),T1为最优投放时间,在未投放新产品的情况下,可以计算所有阶段的旧产品扩散情况,即旧产品在社会网络中的激活情况是已知的参数,令零一系数Sit表示这一参数,即在第t阶段且新产品未投时,节点i是否被旧产品激活。定义系数：θi为节点i的阈值；wji为j对i的影响力；p为更新产品的种子投放数量；C1为旧产品的单位利润,C2为更新产品的单位利润。0-1变量Xit表示第t阶段时更新产品或旧产品是否激活节点i,即阶段t时,i是否已购买更新产品或旧产品；0-1变量Ut表示第t阶段是否投放更新产品,决定更新产品的投放时间T1；0-1变量Zit表示第t阶段是否将i作为更新产品的种子。在产品扩散中：未激活节点的邻居观察自己收到的影响力是否超过自己的固定阈值,如果“是”则该邻居被激活,如果没有新的邻居被激活则扩散结束；更新产品投放时,旧产品停止扩散。综上定义,LTSSOUP 的零一整数规划模型(P)为：

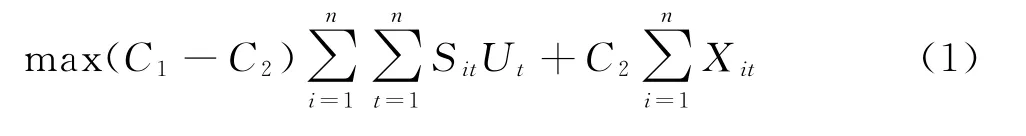
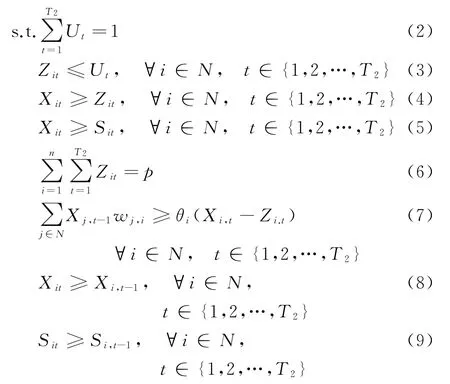
模型(P)中：目标函数式(1)表示所有产品利润最大化,由于包括旧产品与新产品的激活用户数,故在式(1)左边式子中用(C1-C2)扣除重复计算的利润；约束式(2)表示在[1,T2]的某一阶段投放更新产品；式(3)表示只能在Ut=1的阶段投放更新产品的种子；式(4)表示初始种子自动为激活状态；式(5)表示Xit继承旧产品的激活状态；式(6)表示更新产品的初始种子数量为p；式(7)表示节点i被激活必须满足两个条件之一：一是节点i是种子节点,二是节点i来自于已激活邻居的影响力超过阈值；式(8)、(9)表示保证已激活的节点始终保持激活状态。在本研究中,假定旧产品可以促进更新产品的传播(例如,初代的良好口碑推动了后续产品的市场影响力)。因此,在式(7)中,影响力的计算考虑了所有Xit=1的邻居,而Xit既反映了更新产品的激活状态也反映了旧产品的激活状态。

2 算 法

这一部分将介绍一种多阶段贪婪算法(MSDG Multiple Stages Greedy Algorithm,MSDG),该算法的基本思想是：计划期限T2内的某一阶段迭代选取新产品种子,并重新计算其他所有候选种子的边际影响力,计算出所有情况的总收益,找出使总收益最大更新产品种子的投放阶段和种子；同时,也提出了一种快速更新边际影响力的方法,这种方法避免了重复的仿真传播计算。

正如Swaminathan[32]所描述的,在确定性阈值的社会影响力最大化模型中,候选种子的边际影响力由计算得出。其中：(j,i)表示候选种子所有的传播路径上的弧,θi为节点i的当前阈值。假定旧产品对更新产品有促进作用,节点阈值会降低,当一个新产品种子的影响力到节点i时,MSDG 算法将会更新i节点的阈值至θ′i。然后,MSDG 算法会更新传播路径上能抵达i节点的所有候选种子(定义为传入候选种子i)的边际影响力。算法1模拟在产品全生命周期中任意阶段加入第2代产品种子的扩散过程,调用算法1.1获得第2代最优种子,计算出所有情况的总收益,得出使总受益最大的第2代最优的种子和其加入的最优阶段；算法1.1计算当前候选种子的边际影响力、计算加入一个最优种子后的所有候选种子矫正了的边际影响力,采用基于边际影响力纠正的贪婪算法进行种子选取。

算法1最优投入阶段与最优种子优化主程序。

输入旧种子当前激活节点集合N,旧产品节点激活状态R,更新产品种子数量p,旧产品和新产品单个收益C1和C2,影响力权重w,计划阶段限制T2,阈值θ,社会网络图G(N,E)。

输出最优投入阶段T1与最优种子S*。

步骤1扩散旧产品,计算投放扩散期限Steptime；初始化所有阶段投放旧产品的总利润Steptime(t)=0,初始化新产品投放时间t=0,初始化最优种子S*=[]。

步骤2t=t+1。计算旧产品扩散到阶段t时的所有节点激活状态R,令ActiveNum1=以及所有节点受到的影响力Infed和剩余阈值θ′；计算新产品的扩散阶段限制T3=T2-t。

步骤3调用算法1.1节的边际影响力纠正贪婪算法(IRG)计算在t投放的优选种子S(t)；将旧产品已激活的节点与新种子合并,S(t)=S(t)∪{i|Ri=1,i∈N}；模拟扩散过程,计算新产品投放后的激活节点数量ActiveNum2。

步骤4计算在阶段T1投放的总收入

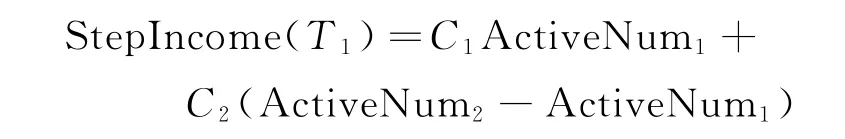
步骤5若t＜Steptime,则返回步骤2；否则,令T1=arg maxtStepIncome[t],S*=S[T1]。

算法1.1基于影响力纠正的种子选取算法。

输入旧产品节点激活状态R,更新产品种子个数p,影响力权重w,新产品的扩散阶段限制T3,当前阈值θ′,社会网络图G(N,E),候选种子节点s。

输出选取的种子集合S。

步骤1初始化种子集合S=∅,信息词典Inform={}。

步骤2对所有的候选节点i,计算边际影响力MI[i],并更新信息词典：

(1)构造一个初始队列Q={s},初始化s的边际影响力MI[s]=1,备份阈值θ′=θ,初始化信息词典Inform={}；

(2)从队列Q中取一个节点u=Q.get()；

(3)对所有的z∈N+(u)且满足Rz=0与z∉List Path,执行：更新扩散阶段,如果L[z]＜L[u]+1,则L[z]=L[u]+1；如果Wuz≥,则MI[s]=MI[s]+1,同时更新信息词典(将[s,u,1]加入词典Inform[z])并将z加入列表(若L[z]≤T3-1,则Q.enqueue(z)),如果Wuz＜,则,同时更新剩余阈值

(4)若队列为空集,则计算结束。

步骤3初始化新产品种子数K=1。

用SPSS 13.0统计软件对数据进行分析。将Ⅰ组、Ⅱ组靶区，心脏，患侧肺，健侧肺和甲状腺等数据进行配对t检验分析，以P≤0.05表示差异具有统计学意义。

步骤4选择边际影响力最大的节点所有种子,即s=arg maxiMI[i]；合并种子S=S+s。

步骤5纠正其他候选节点的边际影响力,并更新已激活节点R和信息词典Inform；K=K+1。

(1)构造一个初始队列Q={s},令Rs=1,θ′s=0,初始化节点的扩散阶段L[：]=0,初始化扩散路径ListPath={s}；

(2)从队列Q中取一个节点u=Q.get()；

(3)对所有的z∈N+(u)且满足Rz=0与z∉List Path,执行：更新扩散阶段,如果L[z]＜L[u]+1,则L[z]=L[u]+1；如果Wuz≥则Rz=1,Qz=0,同时将z加入列表(若L[z]≤L[u]+1,则Q.enqueue(z)),并对Inform[z]的第i个元素更新边际影响力,

(4)若队列为空集,则计算结束。

步骤6若K＜p,则返回步骤4；否则,计算结束。

3 计算实验与数值分析

实验用Python编写程序,测试电脑为联想笔记本,配备2.1 GHz CPU(型号为AMD R5 3550H)、16 GB 2400 MHz内存。测试调用Network 程序包(https：//networkx.github.io/)生成网络。在算法比较时,采用Barabasi-Albert[33]模型生成网络(又称无标度网络),该模型的生成过程：每次产生一个节点(直到生成n个节点),每个新节点从现有节点中选择m个节点并相互连接,选择概率与现有节点的个数成正比。在Python 中,生成网络的方法为：nx.barabasi_albert_graph(n,m,随机种子)。旧产品随机种子为50,单位利润C1=1。

表1描述了不限制新产品种子数量的情况下,MSDG、DD、RA 和DG 算法在求解质量上的对比情况。对与最优投放时机相关的参数T2、n、m、p和C2选择不同水平的值,p取值10～200,控制n=1 500,m=3,C2=0.5,T2=10。测试结果发现：MSDG 算法时间复杂度较低,在计算时间上比DG算法提高了84%,具有较高的求解效率；MSDG 算法能够使用更少的种子激活取得更多的激活数量,目标函数值比DD 算法提高了6%,比RA 算法提高了44%,具有较好的求解质量。

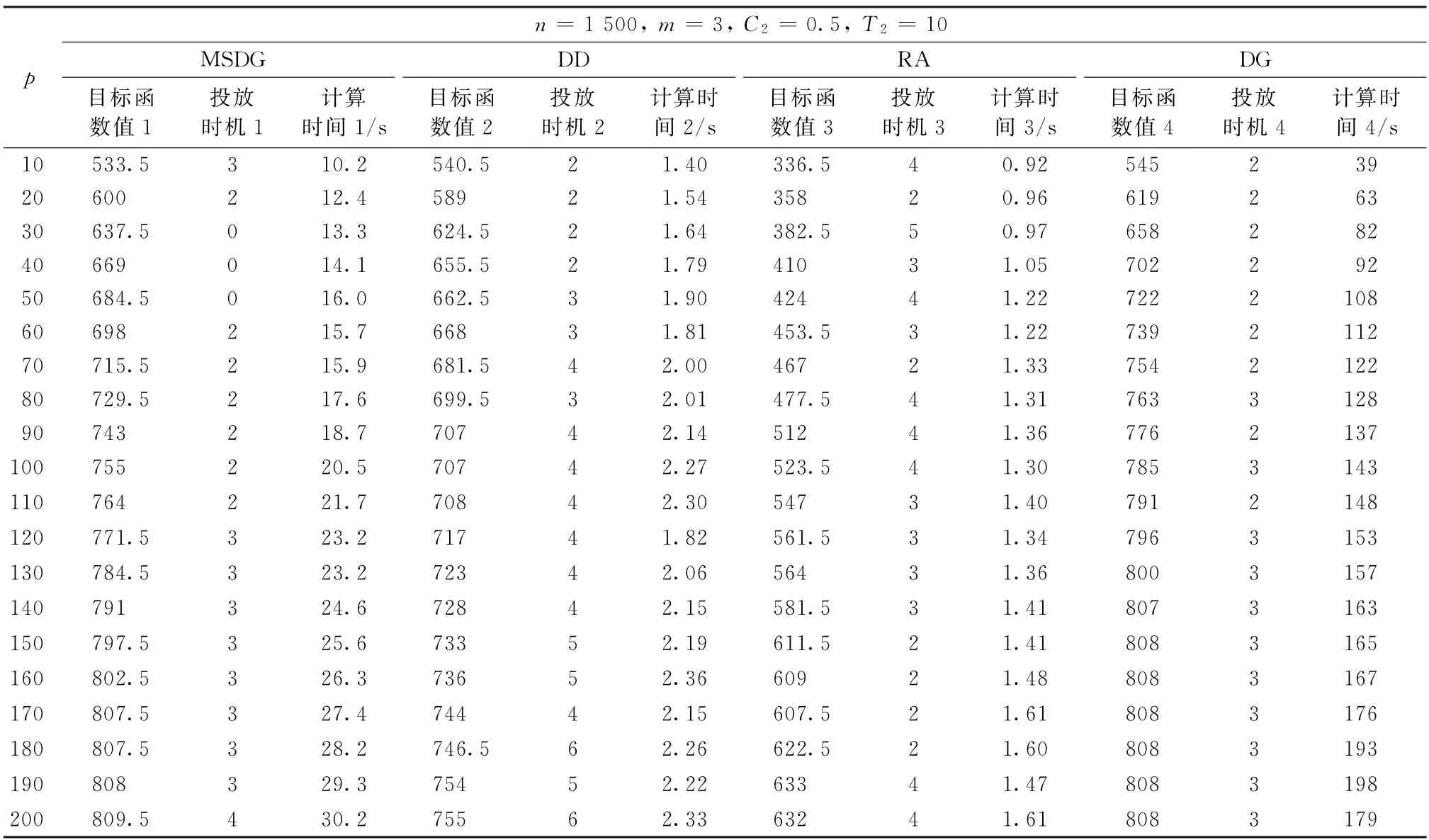
表1 MSDG、DD、RA和DG算法实验结果

同时,本文发现,最优投放时机与更新产品的单位利润、更新产品的种子数量以及计划阶段限制有关系。在测试中,采用一个真实的社交网络数据集Epinions,它是一个基于信任关系的网络,也是一个产品评分网站,用户可以根据产品评价信息选择是否相信其他用户,该数据集来自http：//snap.stanford.edu/data/index.html,常被用于社交网络影响力方面的研究。数据集Epinions有75 879个节点,508 837条边,控制参数C2、p和T2选择不同水平的值。

令p=20,T2=15,最优投放时机随着更新产品单位利润C2的增加而减小,即更新产品利润小时,延期投放使得产品利润更高。但是,随着C2的增加,最优投放时机的减小并不大,尤其是在C2＞C1的情况下,最优投放时机几乎没有变化,如图1所示。

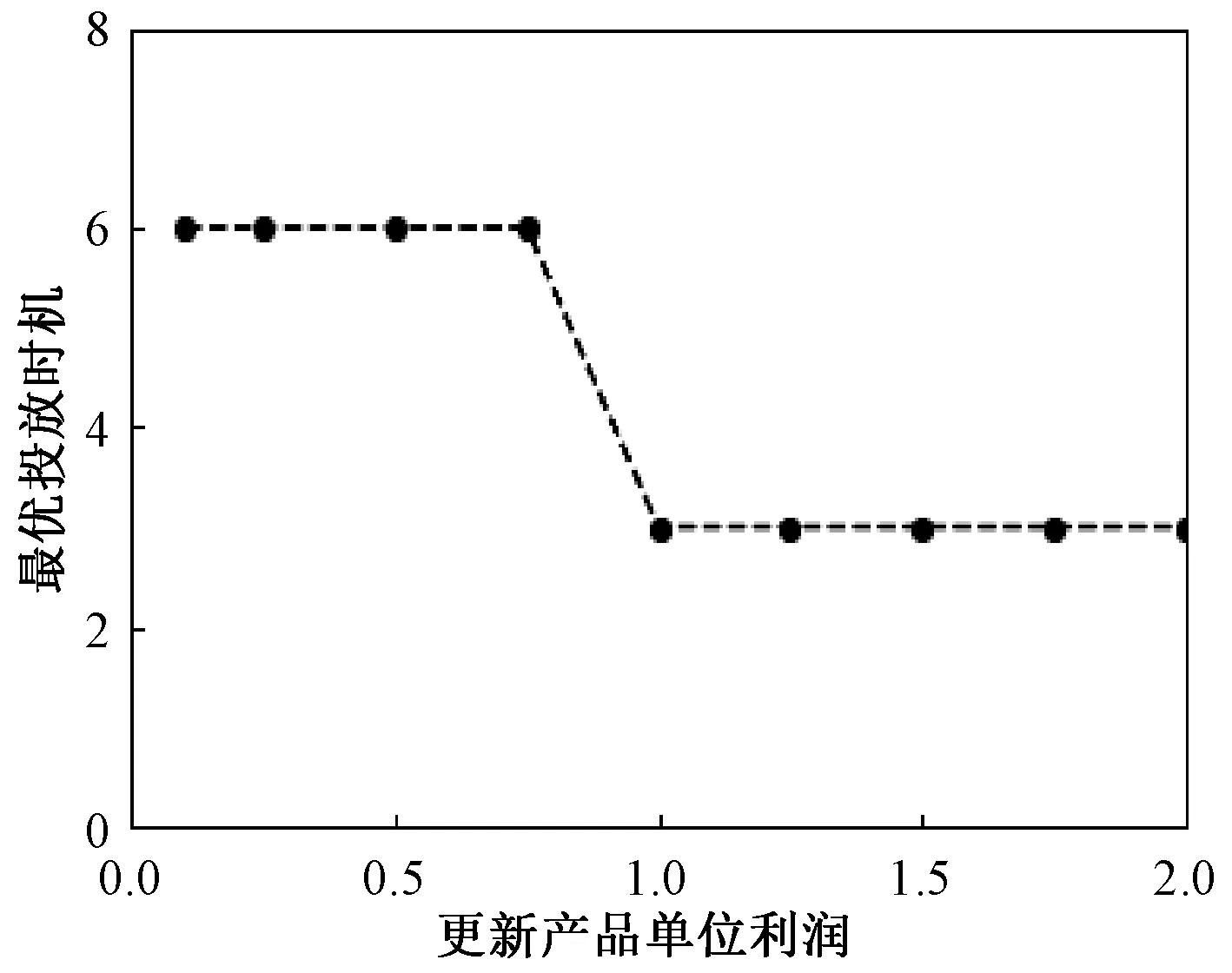
图1 更新产品单位利润对投放时机的影响

令p=20,C2=0.5,最优投放时机随着计划阶段限制T2的增大而明显增大,即计划阶段限制大的产品,延期投放会使得产品利润更高,如图2所示。

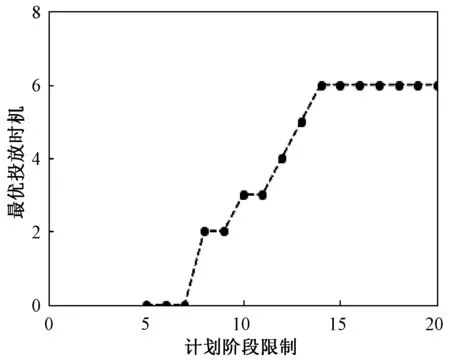
图2 更新产品计划阶段限制对投放时机的影响

令T2=15,C2=0.5,实验发现,最优投放时机随着更新产品种子数量的增加而减少,即更新产品种子数量少的产品,延期投放会使得产品利润更高,如图3所示。

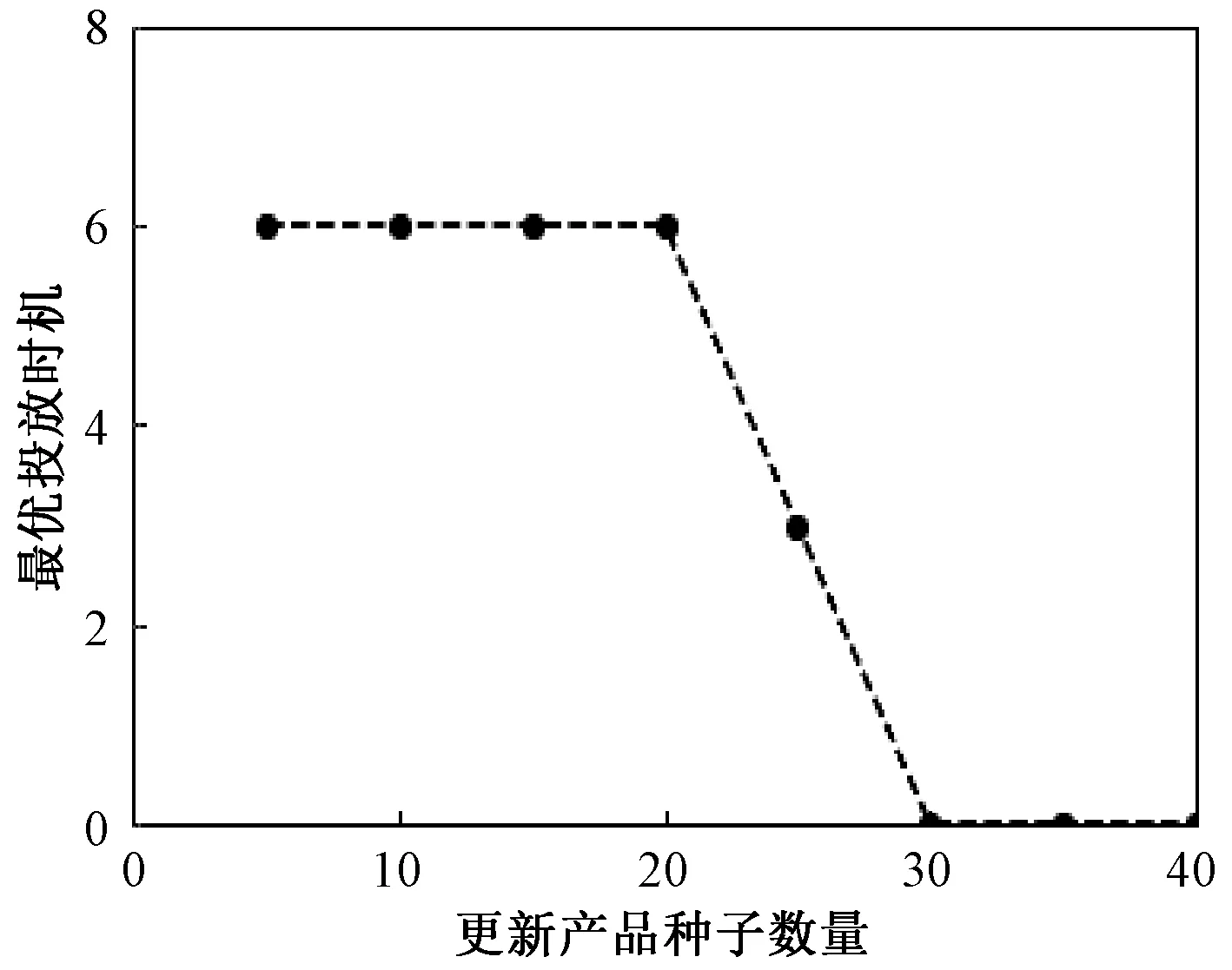
图3 更新产品初种子数量对投放时机的影响

4 结语

本文立足于社会网络的视角,考虑到现实社会中产品的更新换代,提出了相对旧产品何时推出更新产品和选取种子节点使得企业的利润最大的问题。本文建立了LTSSOUP问题整数规划模型,对大规模LTSSOUP 问题设计了MSDG 算法,并将MSDG 算法与DD、RA 和DG 算法进行比较,显示MSDG 算法比DG 算法具有更高的求解效率,比RA 和DG 算法具有较好的求解质量。同时发现,投放时机延后可使厂商获得更高的利润和市场效果,据此在一个真实网络中进行扩散模拟,讨论更新产品最优投放时机与更新产品的单位利润、更新产品的种子数量等因素的关系。针对这些相关因素进行数值分析,发现最优投放时机随着更新产品利润C2、种子数量p的增加而减小,随着计划阶段限制T2的增加而增加。并找出了最优投放时机时选取的最优种子,例如,在现实网络数据集Epinions中,当T2=15,p=10,C2=0.5时,利用MSDG 算法可求得最优投放时机为阶段3,最优的种子节点为[1 677,1 867,8 499,363,2 776,4 125,4 971,8 491,8 918,2 660],可为企业进行网络营销提供决策。然而,本文研究提供的模型只能求解较小规模的问题,多阶段贪婪算法也无法在2 h内求解50 000个节点的实例。因此,下一步的研究将重点针对超大网络规模实例的求解算法。此外,该问题还可以在考虑新旧产品同时扩散的情况开展拓展研究。