解码转发单向多中继网络的能效与谱效权衡

储梦杰，仇润鹤

（1.东华大学 信息科学与技术学院，上海 201620；2.数字化纺织服装技术教育部工程研究中心，上海 201620）

0 概述

随着绿色信息的推广以及通信技术的发展，节能无线通信受到人们的广泛关注。能量效率（Energy Efficiency，EE）是指从发射端到接收端单位能耗成功传输的信息比特数。频谱效率（Spectrum Efficiency，SE）是指单位带宽的平均数据速率［1-3］。协作通信提高了吞吐量、覆盖面和链路可靠性，放大转发（Amplifyand-Forward，AF）和解码转发（Decode-and-Forward，DF）是2 种常用的中继协议［4］，一般情况下，当源节点到中继节点的链路信道质量足够好时，DF 协议的通信性能优于AF 协议，因此，本文对DF 中继网络进行研究。

近年来，学者们对各种中继网络的EE 和SE 进行了研究。文献［5-6］在传输电路功率不可忽略的情况下，通过联合优化时间和传输功率以实现解码转发双向中继系统的EE 最大化，但是它们没有研究SE 优化问题。文献［7］联合优化发射波束形成设计、用户分组、组间时间分配和功率分配，以最大化SE。文献［8］将机会模式选择和发射功率调整相结合，以最大限度地提高瞬时SE 和平均SE。但是，文献［7-8］仅研究SE 优化问题，未对EE 进行分析。文献［9-10］对全双工中继信道不同中继协议下的SE和中继EE 进行研究，但是它们仅研究中继的EE，没有对整个系统的EE 进行分析。

上述文献均对单中继网络进行研究，在中继网络中，通常在源节点和目的节点之间存在多个中继节点。文献［11］研究模拟网络编码的双向多中继系统中EE 和SE 之间的关系，在条件约束下寻找最佳双向SE 以获得最大的EE。文献［12-13］研究AF 多中继网络EE 和SE 之间的最佳平衡问题，但是其以牺牲SE 来提高EE。文献［11-13］没有进行中继选择，在多中继网络中，中继选择可以降低多中继网络的功耗进而优化EE。文献［14］将中继选择和功率分配相结合从而提高无线AF 网络的EE，首先选择最优的中继节点，然后分配所有节点的最优功率从而优化EE。上述文献大多基于AF 进行研究，较少有研究人员分析DF。文献［15］研究在中继发射功率约束以及最小SE 约束下全双工和半双工DF 的EE 最大化问题，但是其未分析EE 和SE 之间的关系。文献［16-18］研究DF 多中继网络，但是其未分析EE 和SE 问题而是对中断概率进行探析。文献［19］研究DF 多跳中继的中断概率最小化问题。文献［20］对采用DF 和AF 协议的多用户多中继网络中用户的最小EE 最大化问题进行研究，通过联合优化中继分配和发射功率来最大化用户的最小EE。

本文研究DF 单向多中继网络的EE 和SE 均衡问题，提出中继选择和功率分配的联合优化方法，并分析节点相对位置不同情况下的EE 和SE 变化趋势。

1 系统模型

如图1 所示，本文单向多中继传输网络由基站、用户和n个中继组成，为便于表述，将基站称为源节点S，用户称为目的节点D，中继称为中继节点Ri，其中，i=1,2,…,n。

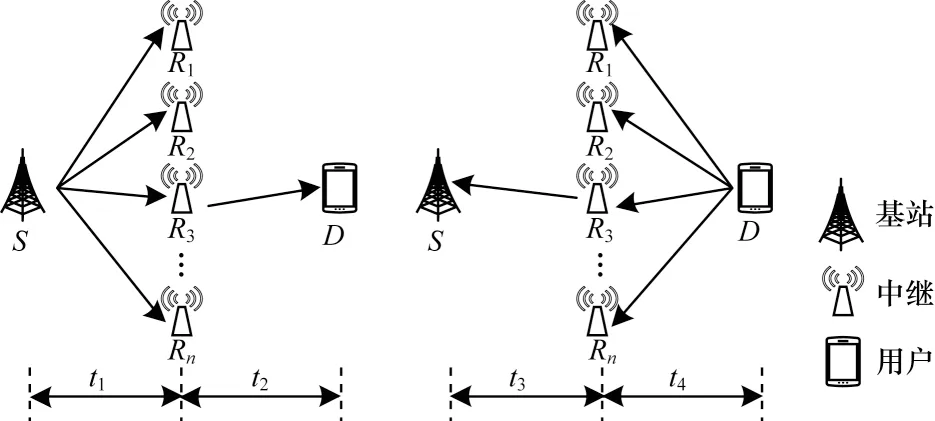
图1 基于DF 的单向多中继传输网络模型Fig.1 One-way multi-relay transmission network model based on DF

源节点S、最佳中继节点Ra和Rb、目的节点D都为半双工传输。假设源节点S和目的节点D之间不存在直连链路，必须通过中继进行数据传输，所有的信道为独立平坦瑞利衰落信道，S到中继Ri的信道衰落系数为hsri，中继Ri到D的信道衰落系数为hrid。假设信道满足互易性，即hsri=hris，hrid=hdri。各节点处的噪声为高斯噪声，独立同分布，均值为0，方差为σ2，其中，源节点S、中继节点Ri和目的节点D处的噪声分别表示为ns、nri和nd。

在第一时隙t1，源节点S发送信号xs给n个中继，中继Ri接收到的信号为：

其中，ps为源节点S处的发送功率。

在第二时隙t2，从n个中继中选取最佳中继Ra，最佳中继Ra将从源节点S处接收到的信号解码，解码后的信号为，将其转发给目的节点D，目的节点D接收到的信号为：

其中，pr为中继节点Ra处的发送功率，假设n个中继的发送功率相等，均用pr表示。

在第三时隙t3，目的节点D将信号xd发送给n个中继，中继Ri接收到的信号为：

其中，pd为目的节点D处的发送功率。

在第四时隙t4，从n个中继中选取最佳中继Rb，最佳中继Rb将从目的节点D处接收到的信号解码，解码后的信号为，将其转发给源节点S，源节点S接收到的信号为：

其中，pr为中继节点Rb处的发送功率，E{|xs|2}=E{|xri|2}=E{|xd|2}=1，E{·}代表期望。

2 中继选择与功率分配的联合优化

源节点S到目的节点D的可实现传输速率表示为Rsd，目的节点D到源节点S的可实现传输速率为Rds，选择Ra和Rb作为最佳中继，根据假设得==pr。参考文献［15］，选择了最佳中继的单向多中继系统端到端的可实现传输速率为：

参考文献［15］，单向中继传输系统的总功率PT表示为：

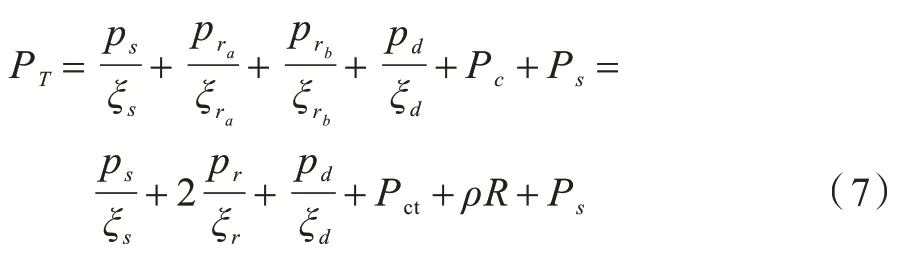
假设系统带宽为单位带宽，单向多中继传输系统的频谱效率SE用ηSE表示，其为系统的总传输速率，即：

单向多中继传输系统的能量效率EE 用ηEE表示，定义为：

单向多中继传输系统联合中继选择和功率分配的EE 优化问题表示为：

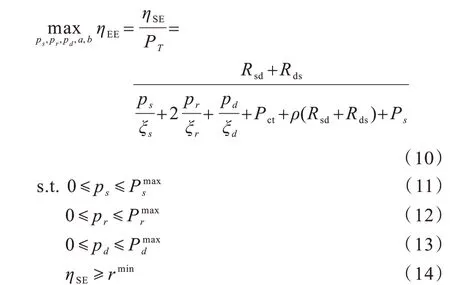
EE 优化需要解决如下2 个问题：

1）选出最佳中继节点Ra和Rb。

2）完成源节点S、中继节点Ri和目的节点D的功率分配。

上述联合优化问题等效为：先对源节点S、中继节点Ri和目的节点D进行最优功率分配，再选出最佳中继节点。优化问题式（10）的功率优化变量有3 个，分别为源节点、中继节点和目的节点的传输功率。为了简化该优化问题，本文引入功率分配因子，各节点的功率分别为：

本文目标是实现EE 和SE 的均衡优化，为了优化SE，令：

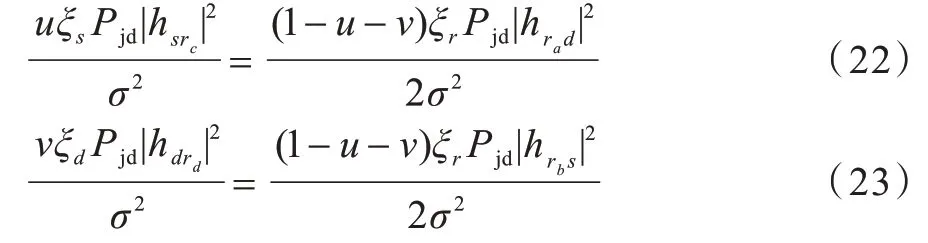
优化问题能够被求解需要满足约束条件Rsd=Rds，联合式（22）、式（23）求出功率分配因子u和v之间的关系，进一步求得：

当满足式（24）时，单向多中继传输系统的SE 取最大值，此时，在最优功率分配下SE 的最优值为：

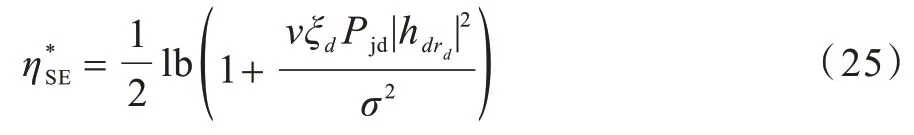
其中，v满足式（24）。

在最优功率分配下，优化问题式（10）转换为：

其中，w(˙)为朗伯函数。

2）计算ηEE在边界点上的取值。

3）对比极值和边界点取值，两者中取值较大的即为最优解。

假设步骤1）获得了最终的最优解，标记为，将其代入式（26），可以得出：

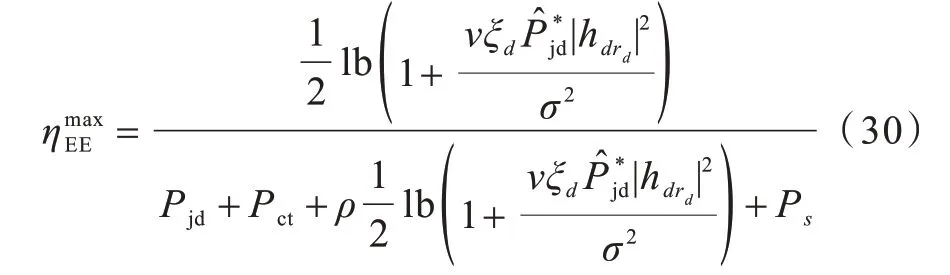
此时最优解中a、b仍是未知的，比较不同中继的最佳EE 值，可以选出最优中继，如下：

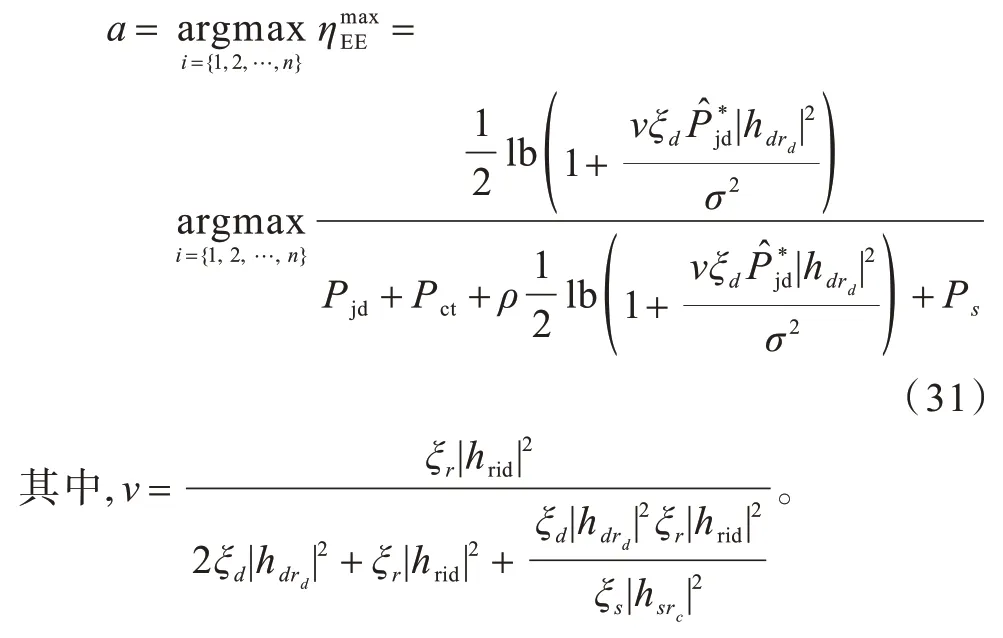
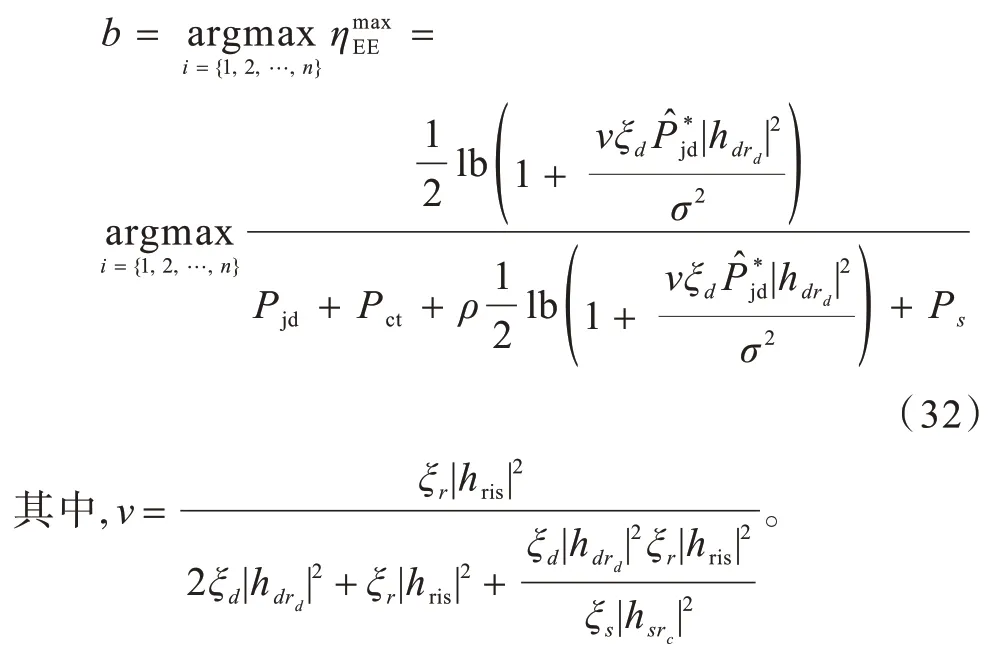
联合优化的实现步骤为：

1）根据式（31）和式（32）选出最优中继。

2）根据式（15）～式（17）以及优化问题式（26）完成功率分配。

3 仿真结果与分析

本文采用MATLAB 进行仿真实验，在单向多中继网络中，设置不同的平均信噪比和不同的节点之间相对位置，将本文所提中继选择与功率分配联合优化方法与现有优化方法进行性能对比，对比方法包括最佳中继等功率分配、随机中继等功率分配和仅最优功率分配3 种方法。各节点处功率放大器效率的合理范围为0.311～0.388［21］，因此，将ξs、ξr和ξd均 设置为0.35。仿真相关参数设置如表1 所示。

表1 仿真参数设置Table 1 Simulation parameters setting

图2 所示为各节点的相对位置，考虑一个包含3 个中继节点的多中继网络，为便于分析，用坐标来表示各个节点的位置，源节点S的位置坐标为（0，0.5），目的节点D的位置坐标为（1，0.5），3 个中继节点R1、R2和R3的位置坐标分别为（x，0.5）、（x，0.25）和（x，0）。

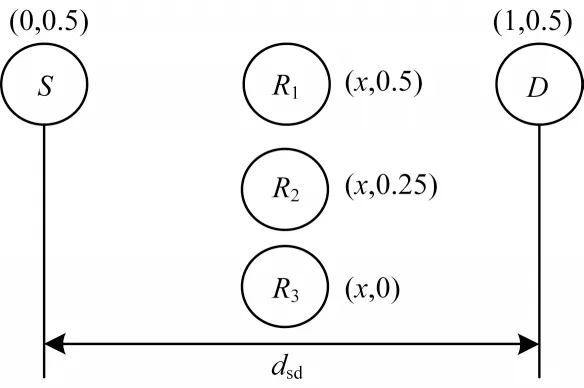
图2 节点位置部署示意图Fig.2 Schematic diagram of nodes location deployment

图3 所示为系统EE 与平均信噪比的关系。设置中继节点的横坐标x=0.6，从图3 可以看出，当平均信噪比增大时，系统EE 先增大后减小，且存在一个最大值，平均信噪比和节点总功率呈线性关系，即存在一个最优的节点总功率使EE 达到最大，与理论分析一致。

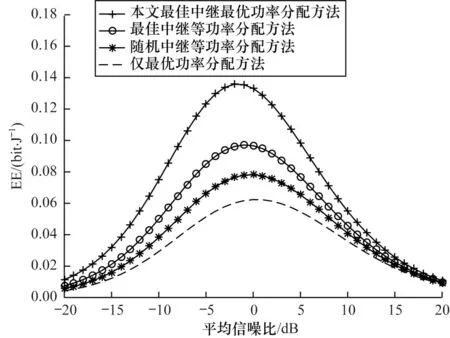
图3 系统EE 与平均信噪比的关系Fig.3 Relationship between system EE and average SNR

图4 所示为系统SE 与平均信噪比的关系。从图4 可以看出，当平均信噪比增大时，SE 一直增大，即SE 会随着节点总功率的增大而增大。

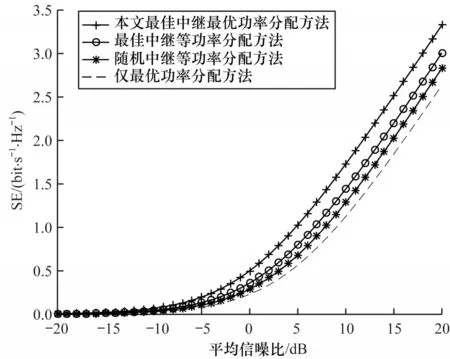
图4 系统SE 与平均信噪比的关系Fig.4 Relationship between system SE and average SNR

从上述实验结果可以看出，本文中继选择与功率分配联合优化方法可以达到最优的分配性能，最佳中继等功率分配方法次之，仅最优功率分配方法性能最差。

图5 所示为不同中继位置情况下单向多中继系统的EE 随SE 的变化情况。从图5 可以看出，随着SE的增大，EE 先增大后减小，当中继节点距离源节点越近时，EE 越高。EE 和SE 之间的关系表明，当增大节点总功率时，SE 会增大，但是超过最优节点总功率时，EE 会减小，此时虽然改善了SE 但是损失了EE，若要系统最优，则通常会损失一些SE 来优化EE。

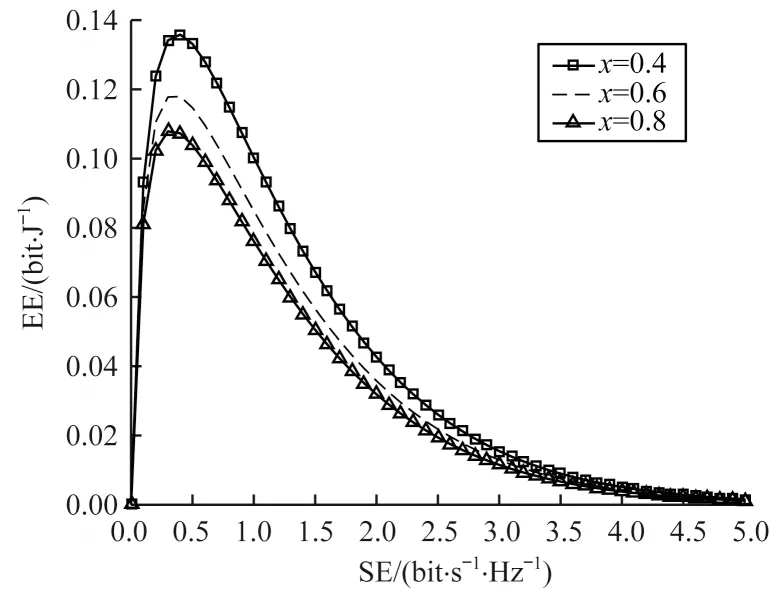
图5 不同中继位置情况下EE 和SE 的关系Fig.5 Relationship between EE and SE under different relay locations

图6 和图7 所示分别为单向多中继系统各节点相对位置不同情况下的EE 和SE。将中继网络中源节点S和目的节点D的位置固定，3 个中继节点R1、R2和R3的位置为变量，分别表示为（x，0.5）、（x，0.25）和（x，0）。当x改变时，中继节点与源节点和目的节点之间的相对位置会发生改变。从图6 和图7可以看出，在本文中继选择与功率分配联合优化方法下，当中继从源节点和目的节点的中间向两端移动时，EE 和SE 均先增大后减小，并且中继选择与功率分配联合优化方法下的EE 和SE，总是优于最佳中继等功率分配、随机中继等功率分配以及仅最优功率分配3 种方法下的EE 和SE。

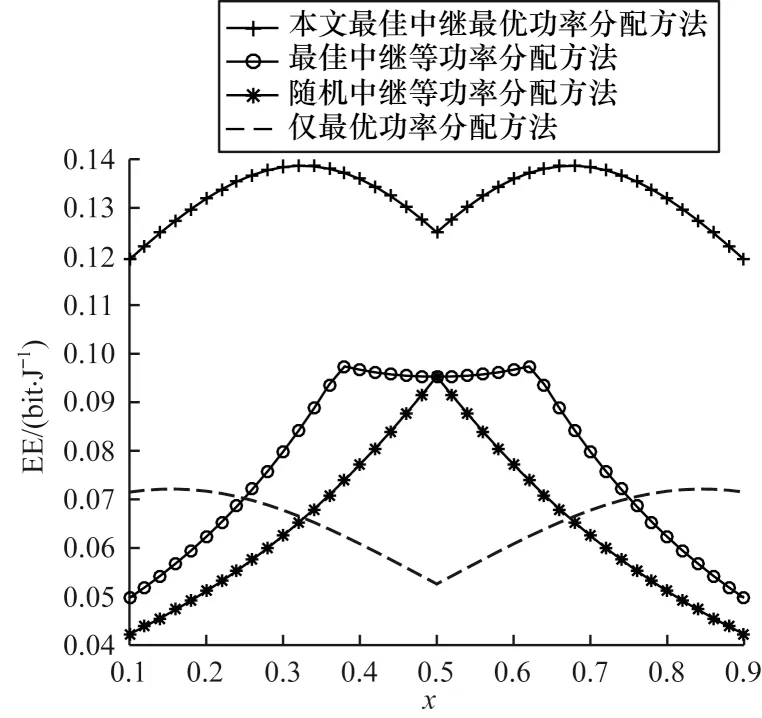
图6 系统EE 与中继位置的关系Fig.6 Relationship between system EE and relay locations

图7 系统SE 与中继位置的关系Fig.7 Relationship between system SE and relay locations

4 结束语

本文研究解码转发单向多中继网络，提出一种中继选择与功率分配的联合优化方法，通过最优功率分配和最佳中继选择实现EE 和SE 的均衡优化。实验结果表明，相比最佳中继等功率分配、随机中继等功率分配以及仅最优功率分配3 种方法，该方法能够有效提高系统的EE 和SE。下一步将研究解码转发全双工多中继系统EE 和SE 的均衡优化问题，通过节点发射功率与中继选择的迭代优化方法实现系统的EE 和SE 最大化。