基于新型自卷积窗和插值补偿的采样方法研究

张国强,李亚琭,胡志远

(北京东方计量测试研究所,北京 100086)

0 引言

在电学计量校准中,同时保证对正弦信号基波幅值测量和信号间相位差测量的准确度,对于测试校准有着十分重要的作用[1-2]。电学测量的主要研究方向之一为通过采样方法获得采样点,再通过采样点分析得到相关电学参数[3]。关于正弦信号幅值[4-5]、双路正弦信号相位差[6-7]的分析方法有多种。这些方法被普遍应用于工频谐波的幅值、频率、无功功率的分析[8-10],以及工频信号的相位差分析[11-12],并有着较高的准确度[13]。但是其主要应用于工频正弦信号的谐波参数分析,无法满足电学计量校准需求。

本文结合了加窗函数法和频谱分析法,并且针对电学计量测试中连续正弦信号的特点,对两种方法进行改进。该方法相比目前已经存在的幅值和相位差测量法,更加适用于对计量校准用的正弦信号进行测量,并且幅值和相位差测量的精度均更高。

1 整周期采样下的幅值、相位差测量

设定通过数字采样得到的双路同频信号,且信号中没有谐波,则其采样数为N的采样序列u1n和u2n可以表示为:

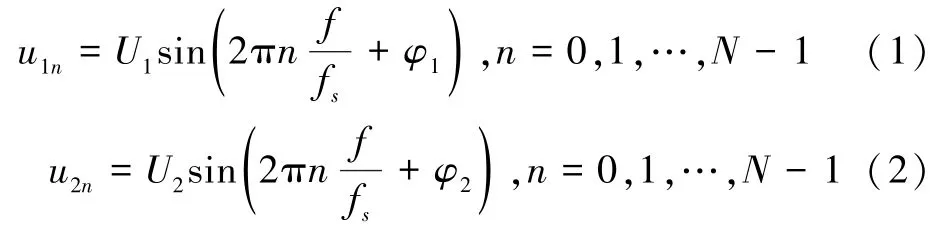
式中:f为信号的频率;U1和U2分别为信号的幅值;φ1和φ2分别为信号的采样初始相位;fs为采样频率。

在数字采样中,如果采样间隔Ts=和信号周期T=之间满足关系NTs=aT(a为正整数),那么采样就为整周期采样。对整周期采样条件下的两路采样序列um n(m=1,2) 作离散傅里叶变换(discrete Fourier tramsform,DFT),则可用式(3)表示为:

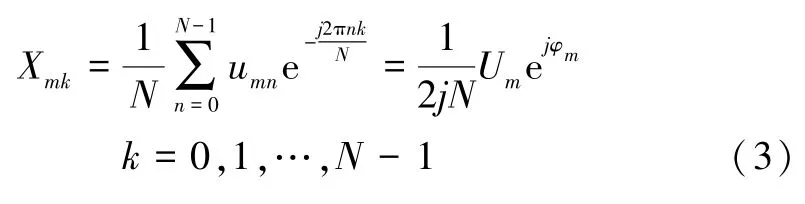
这时,可以直接通过X1k、X2k序列中的最大值位置p以及其所对应的计算出信号的幅值U1和U2,并且信号间的相位差φ=arg(X1p)-arg(X2p)。

2 非整周期采样下的幅值、相位差测量

2.1 DFT 频谱泄漏

在对实际正弦信号进行数字采样时,被采样的正弦信号中存在谐波,且采样条件基本为非整周期采样NTs=(a+Δ)T(a为正整数且＜1)。双路信号的采样序列u1n和u2n通过DFT 后,就会存在频谱泄漏[14]。选择u1n进行分析,并设=τ,那么实际采样序列通过DFT 变换后的如式(4) 所示。其中,m为谐波次数。

此时,对于基波信号,其误差e可以通过理想情况下的DFT 与实际采样的DFT 作差得到。

分析式(5),可将基波的测量分为三部分误差。长范围泄漏误差el是由于不同次谐波之间的相互干扰造成的。短范围泄漏误差es是由于采样的栅栏效应导致的信号频谱中峰值点的观测偏差,包括峰值点的幅值、频率以及相位。负频点泄漏误差en也是长范围泄漏的一种。

其中:

为了减少DFT 的运算量,一般采用快速傅里叶变换(fast Fourier transform,FFT)算法代替DFT。FFT 对于采样序列长度,N要求为:N=2x为正整数。

2.2 泄漏的修正方法

2.2.1 新型自卷积梯形窗的设计

本文采用加窗函数消除由于长范围泄漏和负频点泄漏引入的误差。为了保证基波测量的准确性,通过选择参数可调的窗函数[15],采用调节其参数的方式改变其主瓣宽度和旁瓣衰减速度。梯形窗是介于三角窗和矩形窗之间的窗函数。时域长度为M、上底长度为L的离散梯形窗如式(9)所示。

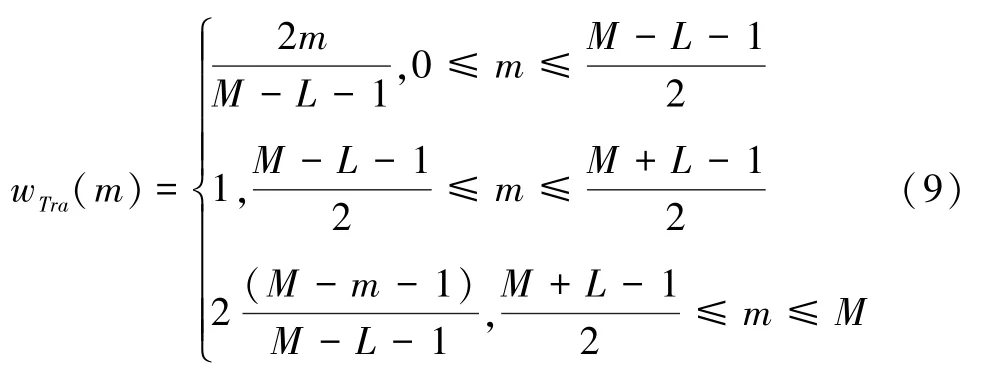
令L和M的比值为ε,即:

当ε 趋近于1 时,梯形窗近似于矩形窗;当ε 趋近于0 时,梯形窗近似于三角窗。通过调节ε,可以改变梯形窗的主瓣宽度、旁瓣峰值电平。

对式(9)所示的离线梯形窗函数施加单位阶跃响应函数u(*)后,再将得到的响应函数通过z变换从离散时域向复频域转化,可得:

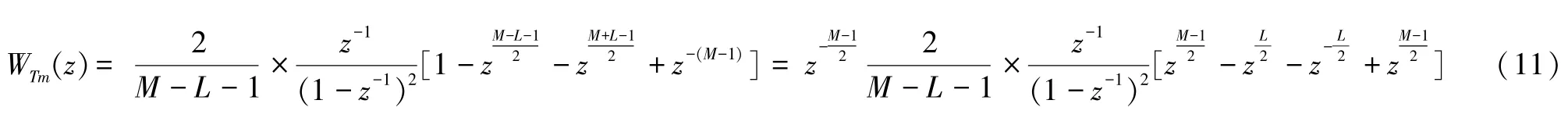
令z=ejω=cosω+j×sinω。将其代入式(11),就能够得到梯形窗的频谱响应函数,如式(11)所示。

通过式(12),可得到梯形窗的主瓣宽度BW=通过调节ε,就可以调节矩形窗函数的主瓣宽度,同时旁瓣的峰值电平Asp(dB)也会变化。为了满足FFT 运算对序列长度的要求,设定时域长度M=1 024,ε取值步长为0.1,观察其旁瓣的峰值电平变化;在τ属于 (0.1,0.2]或[0.2,0.3)中的某一个区间内,取到Asp的最大值衰减值。所以先取ε属于区间(0.1,0.2],得到Asp的最大衰减值。ε对Asp的影响如表1 所示。

表1 ε 对Asp 的影响Tab.1 Effect of ε on Asp

通过表1 可知,选择ε=0.15,此时旁瓣峰值电平为-32.75 dB。

为了进一步减小梯形窗的旁瓣峰值、提高其旁瓣衰减速率,对梯形窗进行自卷积运算,构建新型的梯形窗函数。

通过自卷积窗函数的定义,定义p阶自卷积梯形窗为p个梯形窗进行卷积运算,即:

对于p阶梯形窗,需要进行(p-1)次自卷积运算,运算后的新型窗函数的长度为pM-p+1。同样,为了便于对窗函数序列进行FFT,所以对最终的卷积结果进行补零,使得离散梯形的自卷积窗wTp(n)的长度满足N=pM。

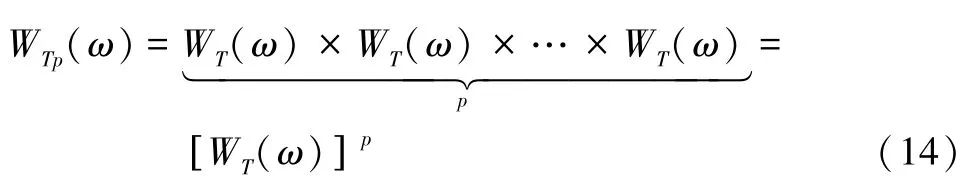
根据式(11)和式(13),可以得到p阶自卷积梯形窗的离散频谱:

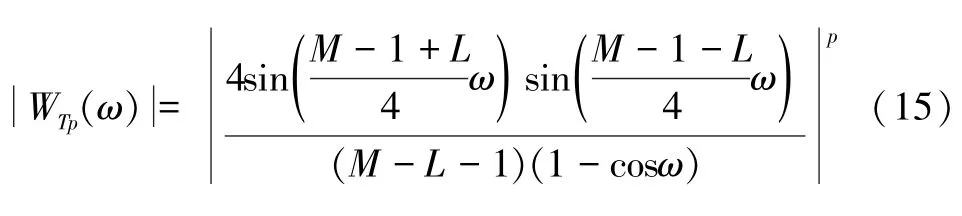
所以,p阶自卷积梯形窗的主瓣宽度为B=1～4 阶且ε=0.15 的自卷积梯形窗的旁瓣峰值电平Asp(dB)与卷积阶数p满足如式(16)所示关系。

2.2.2 谱线插值算法

通过构建新的自卷积梯形窗,利用窗函数的旁瓣衰减特性,能够对非整周期采样下的DFT(FFT)算法中存在的长范围泄漏和负频点泄漏进行抑制。而对于非整周期采样下条件DFT 存在的短范围泄漏误差,则提出谱线插值算法进行修正。

对于非整周期采样条件下的双路信号序列u1n和u2n中的任意一路信号,其基波的幅频信息的谱线应该介于其离散频谱特性中幅值最大和次最大的两根谱线之间。只考虑短范围泄漏,并假设两根谱线分别为第p根谱线和第(p+1)根谱线,基于式(4)进行推导,就可以得出第p根谱线和第(p+1)根谱线的值,如式(17)、式(18)所示:

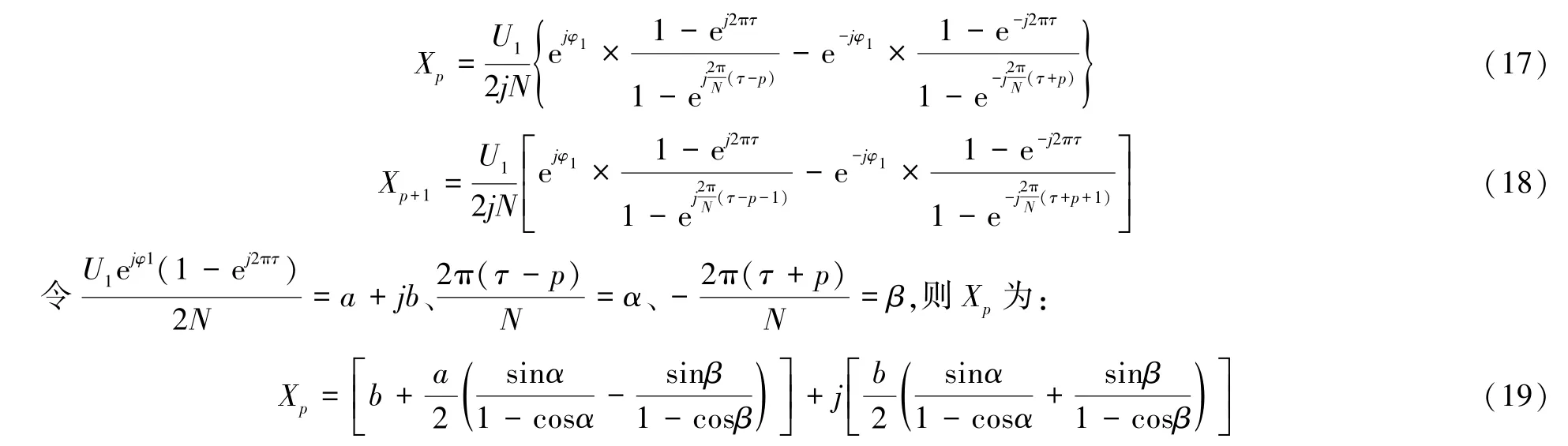
Xp的实部Rp和虚部Ip分别为:

同理,对于第(p+1)根谱线对应的Xp+1,其虚部为:

2.4 血糖（Glu）和皮质醇（Cor） 两组病人组间比较，T3、T4时间点B组Glu和Cor均高于A组，且差异有统计学差异（P＜0.01）。A组Glu于T4时明显高于T1（P＜0.05）；A 组 Cor于 T3、T4时较 T1显著升高（P＜0.01）。 B 组 Glu 于 T2～T4时明显高于 T1（P＜0.01）；B组 Cor于 T3、T4时明显高于 T1(P＜0.01)。 见表 4。

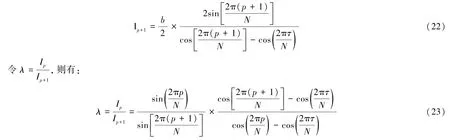
式中:p和(p+1)为基波的幅频特性曲线中幅值最大谱线以及次最大值谱线所对应的位置;N为采样点数;λ为两条谱线所对应的值的虚部之比。其均为已知量,仅τ为未知量。

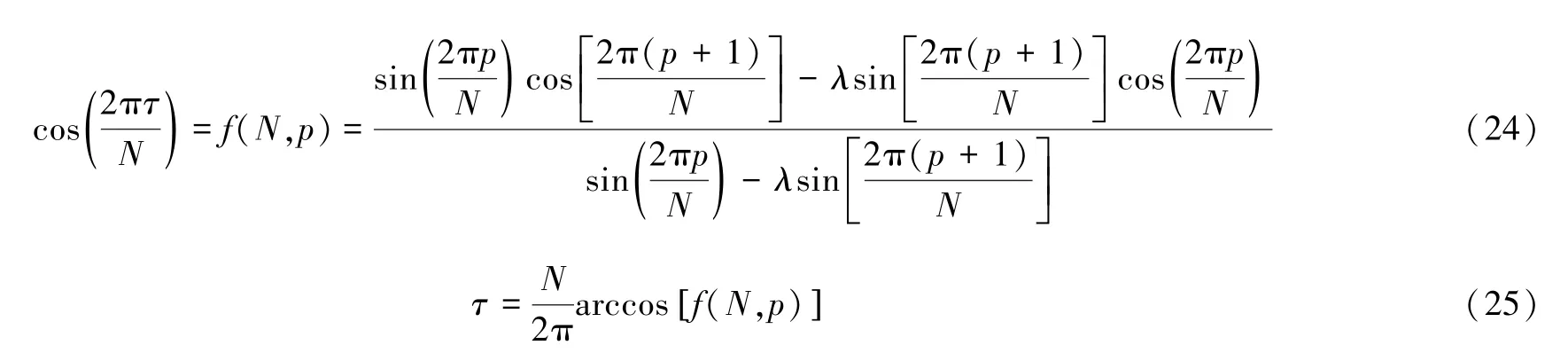
在求出τ之后,就可以求出α、β。再通过式(20)和式(21),可得:

同样地,在求出α、β后,由于Rp和Ip已知,可以反解出a和b的值。

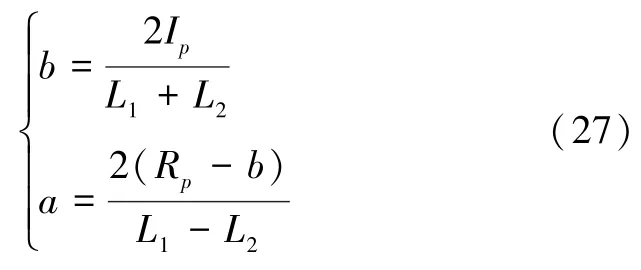
可以计算出该路信号的基波幅值为:

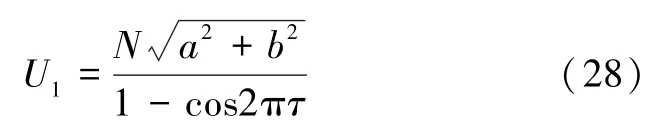
初始相位为:

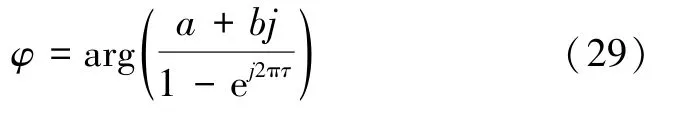
2.2.3 幅值和相位差的精确测量方法

对双路连续正弦信号的基波幅值和相位差,通过采样以及采样算法进行精确测量。所得到的实际双路信号采样图如图1 所示。对于每一次采样,都可以通过加自卷积梯形窗的补偿算法准确测量每一路正弦信号的幅值信息。但是在实际采样中,无法保证采样的起始点能够刚好与信号源发生的起始点重合,而且在第二次采样过程中,前一次采样的数据处理也会使得采样不连续。所以对于单路信号,计算得到的初始相位值均对应采样器进行单次采样的初始相位,初始相位值会持续变化。

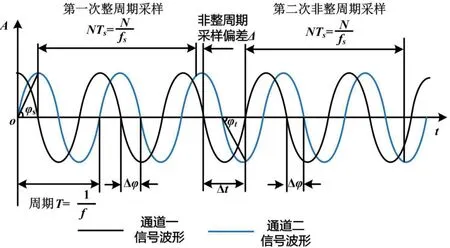
图1 实际双路信号采样图Fig.1 Actual dual signal sampling diagram

虽然采样测量的初始相位会随机变化,但是对于第一次采样,其主要造成的偏差在于采样器进行采样的时间起点延时于信号源发生的起点而产生的相移φs,以及非整周期采样条件下进行DFT 而引入的初始相位测量误差φn。所以,当双路正弦信号同时发生,且通过采样器双路信号同时采样时,其初始相位的实际值φ1、φ2和通过采样得到初始相位测量值φa、φb的关系可以表示为:

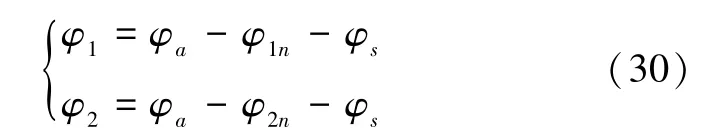
通过本文所描述的补偿算法,可以消除非整周期采样下进行DFT 所引入的初始相位测量误差。基于同时采样的条件,所以两路信号由于信号源发生与采样器采样不同步引起的相移φs相同。两路信号的相位差为:

式中:φ′1、φ′2为通过插值补偿算法求出采样信号序列的初始相位,其中已经不包含非整周期采样下进行DFT所引入的初始相位测量误差。

从第二次采样开始,除了φs与φn,单通道初始相位测量中还存在由于计算上次采样数据而造成的时移产生的相移Δφ。所以对于同频且同时发生的双路信号,对其进行同时采样计算,有:

2 路信号的相位差为:

通过加自卷积梯形窗的补偿算法与采样器的同时采样相结合的方法,可以精确测量两路信号之间的相位差。完整的基于新型自卷积窗和插值补偿的采样方法如下。

①由设定好采样频率和采样点数的数据采集系统,对双路正弦连续信号进行同时、连续采样,在每个采样循环中生成一组带有双路信号采样值的离散序列。②将离散序列进行加自卷积梯形窗的FFT 变换。③查找FFT 变换后,双路信号各自频谱中幅值最大的谱线以及幅值次最大的谱线,记录其位置和以及两条谱线各自实部和虚部的大小。④通过算法描述计算τ。⑤利用τ计算双路信号基波幅值的准确值U1、U2,和消除了DFT 误差的信号采样初始相位φ′1、φ′2。⑥直接作差,计算两路信号的相位差φ。

3 试验验证

为了验证自卷积梯形窗及谱线插值补偿方法的有效性,并且针对交流电阻中对于基波测量准确度的需求,通过Matlab 生成离散序列模拟非整周期采样下,带有微小谐波分量的类正弦波形信号,再通过传统的DFT 算法和本章所设计的自卷积梯形窗三谱线插值算法进行对比。其中,自卷积梯形窗为三阶。假设被测信号为:

设定信号频率f=101 Hz、采样频率为1 kHz,正弦信号的基波仿真计算结果如表2 所示。通过分析2n(n=7,8,9,10)个采样点,使其满足FFT 算法的点数要求。通过分析基波(1 次谐波)的数据,验证补偿算法是否能够消除传统DFT 在非整周期采样下存在的长范围泄漏、负频点泄漏以及短泄漏问题。

表2 正弦信号的基波仿真计算结果(f=101 Hz,fs=1 kHz)Tab.2 Fundamental wave simulation results of sine signal(f=101 Hz,fs=1 kHz)

由表2 可知,相对于传统的傅里叶变换,设计的补偿算法能够极大地提高测量双路正弦信号的基波幅值、相位差的准确度。随着采样点数的增加,自卷积梯形窗函数的主瓣宽度更窄,旁瓣衰减更快。其抑制频谱泄漏的能力就越强,算法就能够更加准确地测量正弦信号的基波幅值信息和初始相位信息。标准源法校验补偿算法幅值测量准确度如图2 所示。

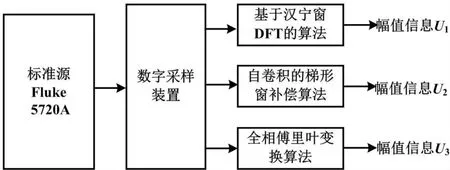
图2 标准源法校验补偿算法幅值测量准确度示意图Fig.2 Accuracy of the amplitude measurement of the compensation algorithm using the standard source

为了验证补偿算法在实际测试中幅值测量的性能,采用标准源法对算法进行测试。使用标准信号源Fluke 5720A 作为试验的标准信号输出仪器。使用LabVIEW,通过编程实现算法;同时,令该程序能够驱动波形采样的硬件设备,形成一台虚拟采样测试仪器。测试仪的程序中同时写入加汉宁窗的DFT 算法和全相傅里叶变换算法,与本文设计的自卷积补偿算法进行对比。

设定标准源的幅值输出范围为1～4 V,输出间隔为0.5 V,频率分别为100 Hz、1 kHz、10 kHz 和100 kHz。使用标准源法验证算法的准确性,将标准源5720A 的示值Vr作为真值,Vx则是通过采样算法计算得到的实际测量值。相对误差δ可通过式(37)计算:

测试完成后,4 个频率点下的试验数据结果如表3～表6 所示。

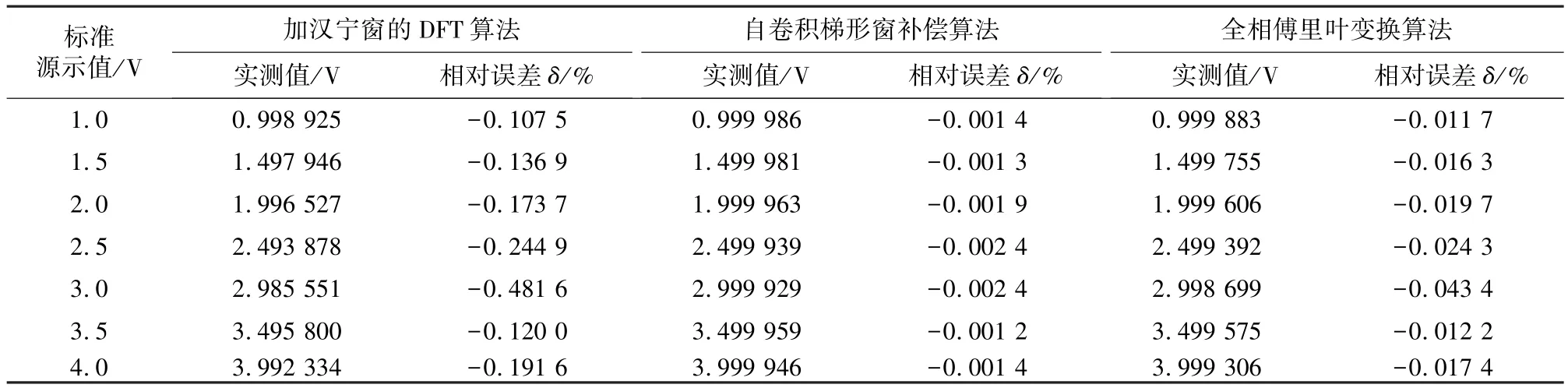
表3 标准源法Fluke-5720A 校准算法幅值测试准确度(100 Hz)Tab.3 Fluke-5720A calibration algorithm based on standard source method(100 Hz)

表4 标准源法Fluke-5720A 校准算法幅值测试准确度(1 kHz)Tab.4 Fluke-5720A calibration algorithm based on standard source method(1 kHz)

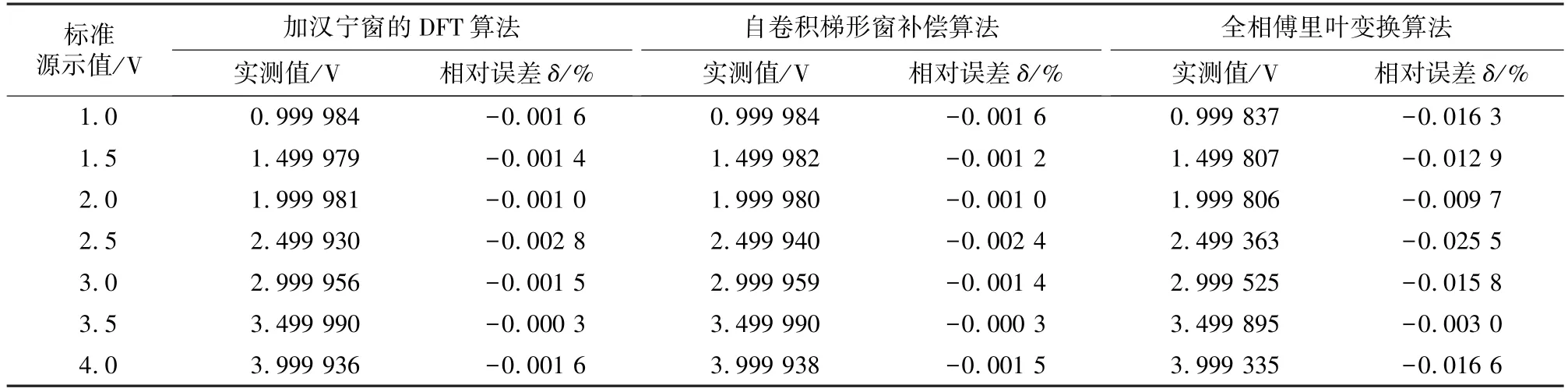
表5 标准源法Fluke-5720A 校准算法幅值测试准确度(10 kHz)Tab.5 Fluke-5720A calibration algorithm based on standard source method(10 kHz)

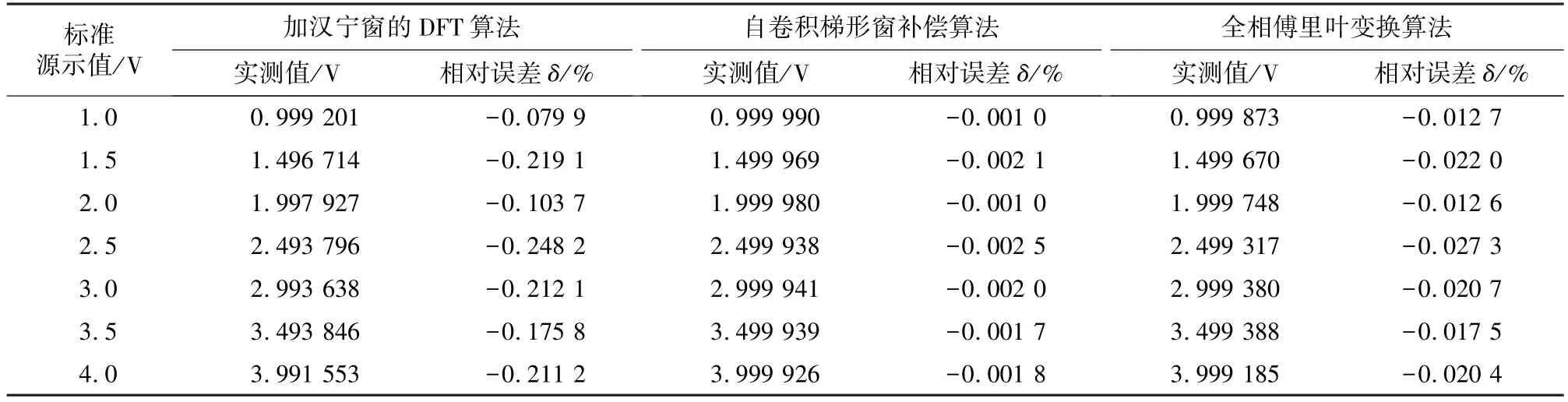
表6 标准源法fluke-5720A 校准算法幅值测试准确度(100 kHz)Tab.6 Fluke-5720A calibration algorithm based on standard source method(100 kHz)

通过对比表3～表6 数据可以看到,在100 Hz～100 kHz 频率范围内和1～4 V 幅值范围内,3 种算法均有良好的稳定性。对于标准源5720A 基波的测量,使用自卷积梯形窗补偿算法的测量误差在0.001%附近;全相傅里叶变换算法的测量误差比补偿算法高1 个数量级,测量误差在0.02%左右;加汉宁窗的DFT 算法误差仅为0.1%左右。所以,自卷积梯形窗补偿算法能够准确测量幅值准确度,运用在虚拟仪器技术中,能够对信号源输出的正弦信号的幅值进行更加精确、稳定的测量。

4 结论

本文针对电学计量中双路连续信号的幅值和相位差的准确测量,在双路正弦信号存在谐波的情况下,分析了非整周期采样条件下使用传统DFT 算法分析正弦信号存在的误差。通过调节梯形窗参数和对梯形窗进行自卷积运算得到的新型窗函数,对误差中存在的长范围泄漏和负频点进行抑制。采用加窗FFT 后的序列中最大的两根谱线,并直接通过数值运算对误差中的短范围泄露进行补偿,提高幅值和相位差测量的准确度。仿真试验表明,所提出的方法对幅值和相位差的测量具有很高的准确度,而实际测量试验则证明了该方法运用在虚拟仪器技术中同样具有更好的准确性和稳定性。