回采巷道侧向支承压力对工作面前方支承压力峰值和塑性区宽度的影响

吴呈哲 刘长武 赵 超3

（1.四川大学水利水电学院；2.水力学与山区河流开发保护国家重点实验室）

在地层中开掘巷道和回采矿石时，巷道围岩和工作面前方必然会出现应力重分布，一般将巷道或采场侧向围岩改变后的切向应力增高部分称为支承压力［1］。通常情况下，由于受到巷道和采空区的联合作用，重新分布后的采场支承压力的峰值位置往往位于工作面前方的拐角附近，其大小对预留矿柱的尺寸以及巷道支护参数的确定起关键作用。因此，研究工作面前方支承压力的分布情况，对矿区安全开采有着重要的实际意义。

多年来，许多学者通过设计不同的力学模型，从理论层面对工作面前方支承压力的分布情况以及塑性区的宽度进行了一系列的分析和探讨。钱鸣高等［1］从平面应变角度，根据工作面前方岩体的极限平衡条件和平面微元体的受力平衡条件，推导了塑性区内支承压力计算公式；靳钟铭等［2］则在此基础上考虑了水平应力的影响，通过微元体平衡，并结合侧压系数，补充了弹性区内支承压力计算公式；侯朝炯等［3］则认为，以上估算支承压力的方案将工作面前方煤体简化为平面应变问题，但却未考虑平面应变问题所需满足的应力微分平衡方程，因此，他从满足应力微分平衡方程的角度出发，并结合相应的边界条件，推导出了不计体积力条件下塑性区内支承压力计算公式；谢广祥等［4］则在此思路的基础上考虑了体积力的影响，进一步推导出了塑性区内支承压力计算公式；袁前进［5］根据煤壁前方煤体的变形特点，将煤体划分为破碎区、塑性区及弹性区，并将煤体的变形过程划分为塑性流动、塑性变形、弹性变形3个阶段，并给出了各阶段煤体强度的本构关系，在此基础上运用极限平衡理论推导出各区段支承压力的理论计算公式；熊仁钦［6］认为将此问题视为平面应变问题不符合实际情况，因此用三向应力状态，结合岩体的极限平衡理论，对问题进行求解，但考虑到求解的难度，忽略了除工作面开采方向外其余2个方向上的应力增量；此外，李洪等［7］考虑了煤帮与顶板的相互作用，提出了支承压力的弹性基础梁计算方法；宋振骐等［8］从支承压力的形成机理入手，通过对支承压力形成的5个阶段进行分析，创新地提出综合移动角起于支承压力边缘的方案，建立了相关的结构力学模型和求解方程；陈忠辉等［9］针对综放开采煤壁前方支承压力的分布特征，应用统计损伤力学建立了一个简单的力学模型，在给定变形条件下研究支承压力的分布规律，避免了对支承压力的分区研究；王卫军等［10］在分析了沿空掘巷应力环境的基础上，应用损伤理论，分析了给定变形下沿空掘巷实体煤帮的支承压力分布。

在这些模型中，有学者考虑了应力重分布后所产生的回采巷道侧向支承压力对于工作面前方支承压力峰值的影响，并认为回采巷道侧向支承压力的存在是导致工作面两端巷道难以维护的关键因素之一［6］，若不考虑回采巷道侧向支承压力的影响，会导致工作面前方支承压力峰值和塑性区宽度的计算值偏小。因此，对于该问题的讨论对实际工程有着积极的指导意义。然而，目前学者们对于相关问题的讨论仅限于将工作面的前支承压力和回采巷道的侧支承压力先分开计算后再进行简单叠加。这种简单叠加的方法只适用于计算工作面前方的支承压力峰值，无法用来计算在回采巷道侧向支承压力已经形成的情况下工作面前方塑性区的宽度。

针对上述问题，本研究基于顶板与矿帮相互作用的力学模型（即地基梁模型）［11］，并综合考虑回采巷道周围所存在的侧向支承压力的影响，推导了相应的顶板位移计算公式，通过该公式可计算矿体的支承压力和塑性区宽度。此外，通过相应的工程实例进行试算，进一步讨论了回采巷道侧向支承压力大小对于工作面前方支承压力峰值以及矿帮塑性区宽度的影响，为确保矿层安全开采打下基础。

1 支承压力理论计算

1.1 力学模型

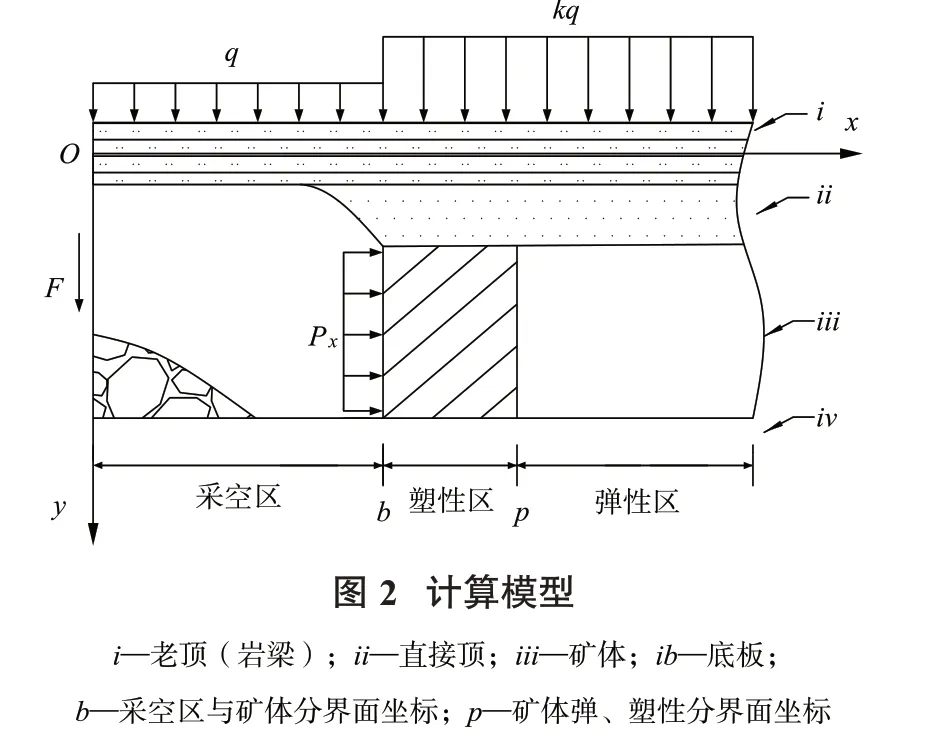
由于回采巷道开挖早于回采作业，且在回采开挖前巷道周围的支承压力分布已趋于稳定，因此，对于回采工作面前方支承压力分布以及塑性区宽度问题的研究应在已处于稳定状态的回采巷道侧向支承压力的环境下进行分析。通过弹性力学方面的相关推导可知，开挖后巷道的支承压力分布情况如图1中“B-B”剖面处的支承压力分布曲线所示。即将巷道周围矿体划分为弹性区与塑性区，并认为支承压力峰值位于弹性区与塑性区相交的区域。基于以上认识，本研究取巷道周围支承压力峰值附近的弹性区内单位宽度的顶板以及矿体（图1中“A-A”剖面右侧）来进行讨论，并将侧向支承压力的影响简化为岩梁上覆荷载的提高，即以巷道侧向支承压力的应力集中系数k来反映回采巷道侧向支承压力的影响，计算模型如图2所示。将顶板视为岩梁，采空区位置的岩梁上方作用有均布荷载q，工作面前方位置的岩梁上方作用有均布荷载k q，矿壁上作用有工作面支护阻力P x。此外，根据铰接岩块假说，采空区上方岩梁端部还受到周期性垮落岩块给岩梁带来的作用力F。

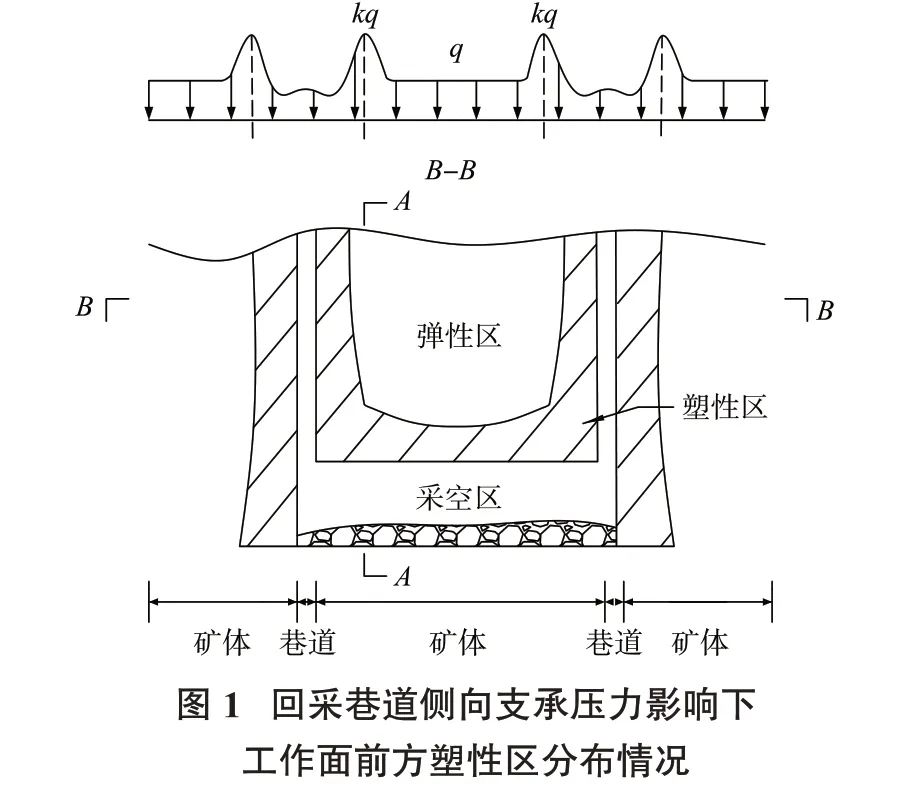
1.2 基本假设

（1）不考虑矿层倾角、老顶自重和矿层自重力的影响。

（2）将回采巷道侧向支承压力对于岩梁、工作面前方矿体的影响综合考虑为岩梁上部荷载的提高，即认为工作面前方矿体上的岩梁上方作用有均布荷载kq，k为巷道侧向支承压力的应力集中系数，其取值受巷道尺寸、巷道形状等因素的影响。

（3）采用地基梁假说来讨论岩梁、工作面前方矿体的相互作用关系。认为塑性区内的矿体处于极限平衡状态，弹性区内的矿体处于弹性状态，并结合矿体中微元体的受力平衡条件对矿体塑性区内支承压力情况进行讨论。

1.3 模型的求解

1.3.1 顶板位移曲线的建立

图2为矿体与顶板受力模型。

在地基梁模型中，挠度与荷载、地基反力σy之间的关系为［10］

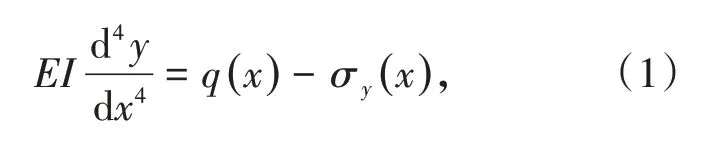
式中，E为岩梁的弹性模量，MPa；I为岩梁的截面惯性矩，m4；x为岩梁的位置坐标，m；y为岩梁的挠度，m。

根据李树清等［12］对于矿体在弹性区、塑性区内应力的分析可知，矿体在塑性区和弹性区内的水平应力和垂直应力分布情况如下。

（1）塑性区。

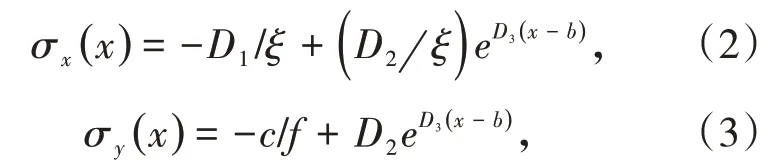
（2）弹性区。

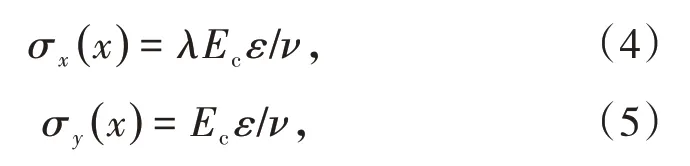
式中，ν=( 1-2μ)( 1+μ)/( 1-μ)，λ=μ/( 1-μ)，μ为矿体的泊松比；Ec为矿体的弹性模量，MPa。

在求得矿体弹、塑性区内的垂直应力分布情况下，可将矿体的垂直应力视为地基梁模型中的地基反力σy(x)，故计算模型可得到简化（图3）。

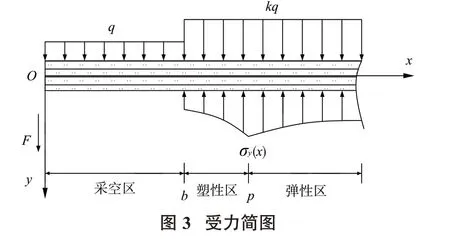
根据此受力简图，可将式（3）、式（5）以及各区域内所对应的荷载条件q、k q分别代入微分方程（1）中进行求解，进而可求得矿体采空区、塑性区和弹性区上方岩梁的位移曲线。

（1）采空区上方岩梁。

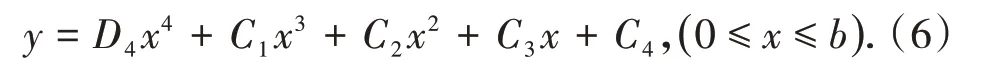
（2）塑性区上方岩梁。

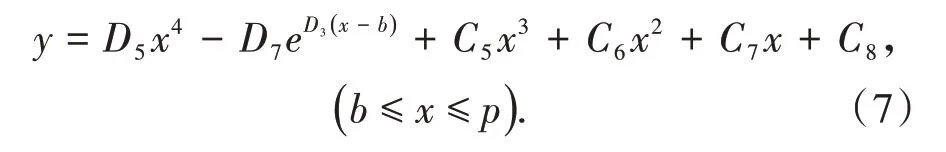
（3）弹性区上方岩梁。

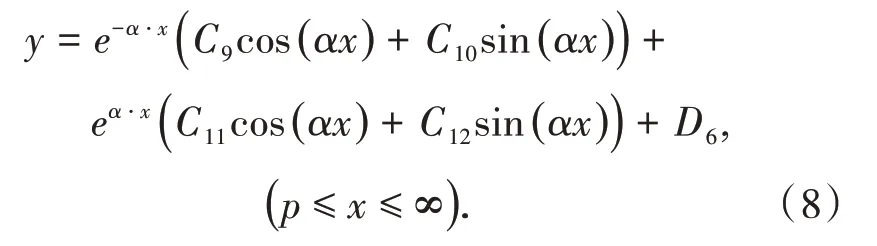
1.3.2 待定系数求解

由于总共有12个待定系数，因此求解需要12个边界条件，具体如下。

（1）采空区上方岩梁端点（x=0）处弯矩为0，剪力为F，则

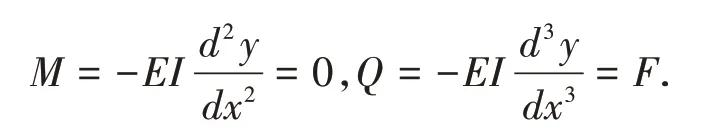
（2）采空区与塑性区上方岩梁交界（x=b）处挠度、转角、弯矩、剪力相等。

（3）弹性区与塑性区上方岩梁交界（x=p）处挠度、转角、弯矩、剪力相等。

（4）弹性区趋于无穷远（x→∞）处岩梁不受采空区影响，位移趋于稳定

将上述边界条件代入式（2）～式（5），可求得各待定系数如下。

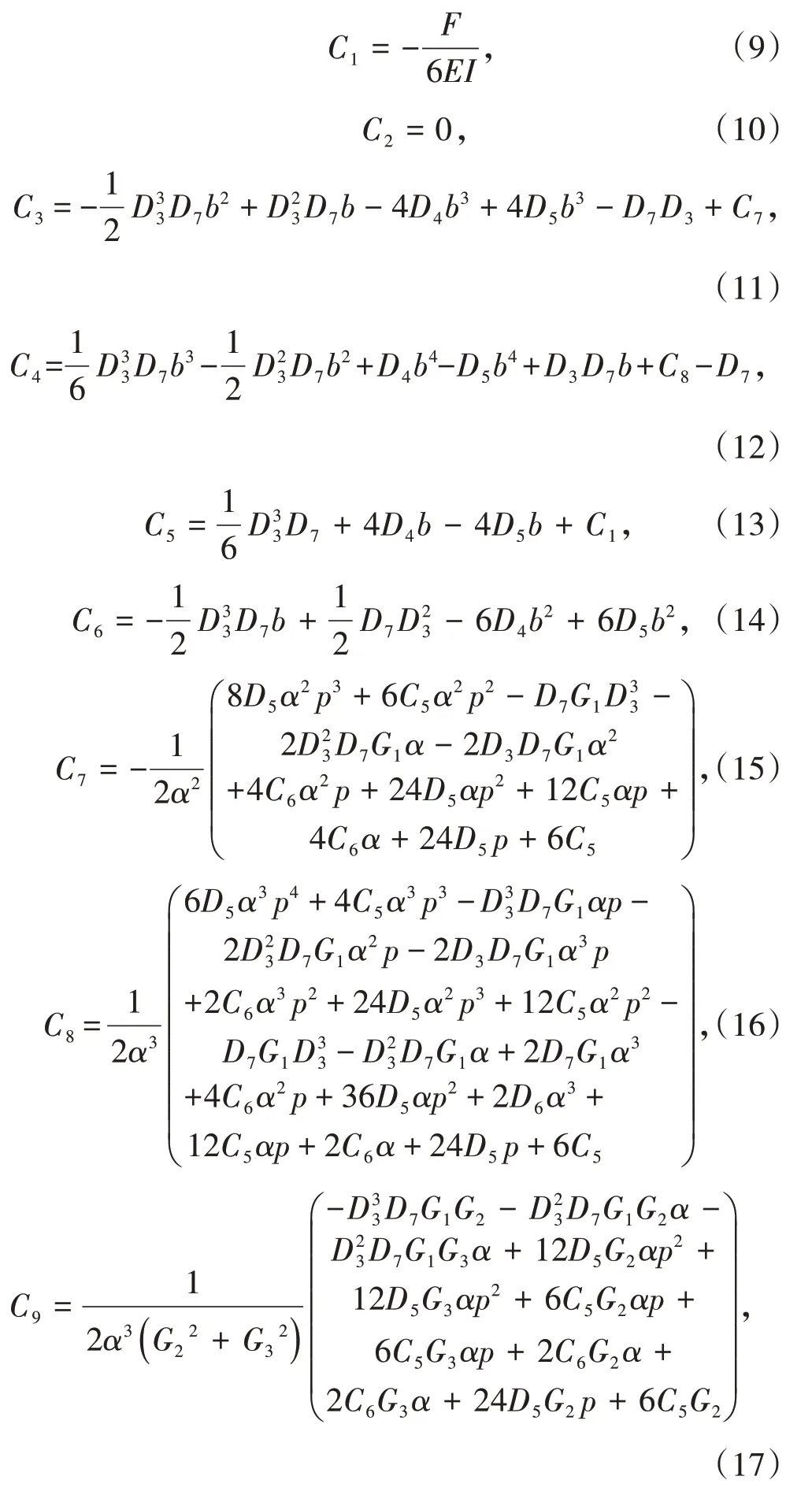
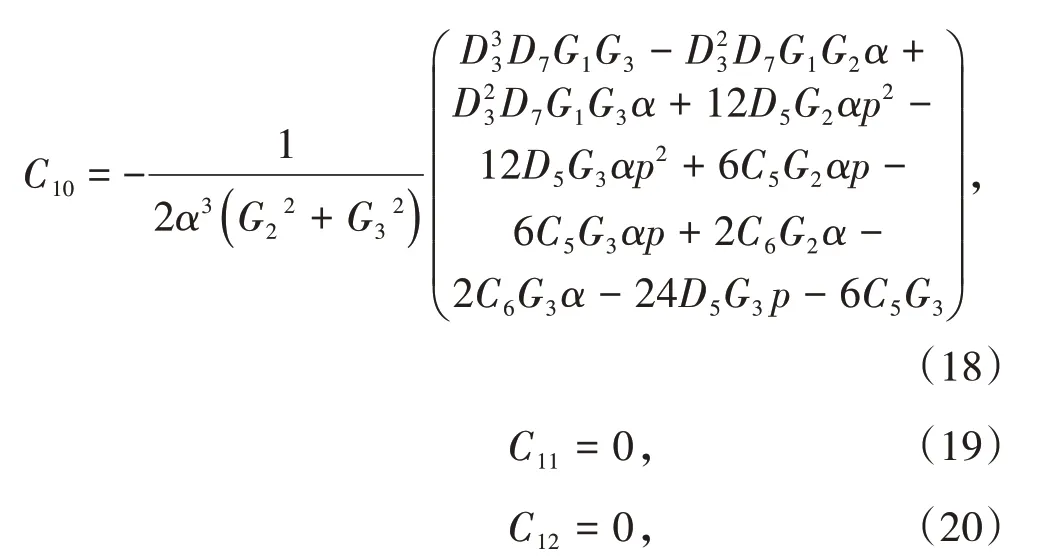
式中，G1=eD3(p-b)，G2=e-αpcos(αp)，G3=e-αpsin(αp)。

在实际计算中，先将相关力学参数代入式（9）～式（20）以求得待定系数C1～C12，进而将所求得的系数C1～C12代入式（6）～式（8），得到考虑了回采巷道侧向支承压力影响的顶板位移曲线。通过该位移曲线可求得顶板各点的位移值，进而可将所求得的顶板位移值代入式（2）～式（5）来求得工作面前方塑性区的宽度以及各位置的支承压力值。

2 工程实例分析

以邢台矿区某首采工作面为工程背景，对巷道侧向支承压力大小对于工作面前方支承压力峰值以及工作面前方塑性区宽度的影响进行分析，相关物理力学参数见表1。其中，老顶为粉细砂岩，宽度取1 m，厚度取6 m，计算得I=18 m4。根据老顶及以上各岩层的容重、弹性模量和厚度进行估算［13］，取q=0.26 MPa。周期性垮落岩块给岩梁带来的作用力F=535.08 kN。

?

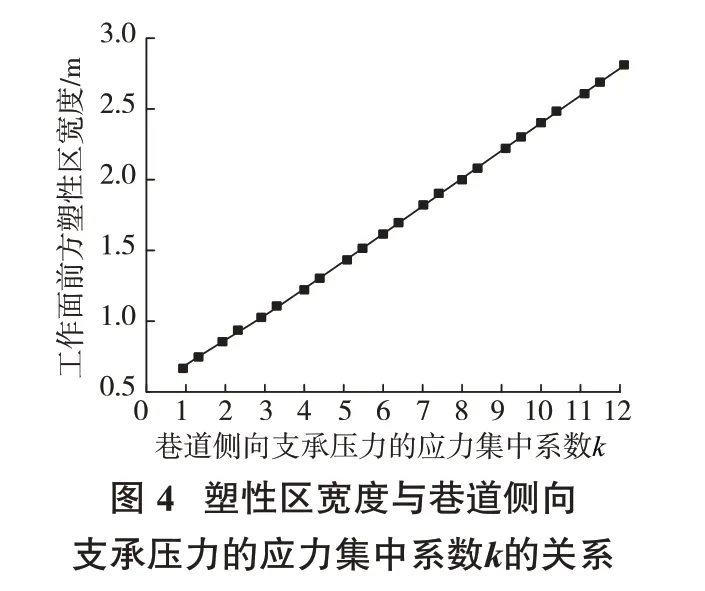
具体计算时，先通过设置一个具体的巷道侧向支承压力的应力集中系数k，再根据矿体塑性区与弹性区交界处水平应力连续这一条件求出不同k值下工作面前方的塑性区宽度，并在此基础上计算该k值下工作面前方的峰值支承压力大小。此外，通过设定不同的k值并分别计算该k值下工作面前方的塑性区宽度及支承压力峰值，并对数据进行拟合，进而分析工作面前方塑性区宽度以及支承压力峰值受k值的影响趋势。本次计算所取的k值以0.5为公差，从1取到12，计算及拟合的结果如图4、图5所示。

根据图4可以看到，工作面前方塑性区的宽度随巷道侧向支承压力的增长而增大，且当k=1（即未考虑回采巷道侧向支承压力影响）时，塑性区宽度为0.492 m。而根据现场实测可知，在周期来压条件下工作面前方的塑性区宽度为2～4 m，因此在进行塑性区宽度计算时，若不考虑巷道侧向支承压力的影响会导致塑性区宽度的计算结果严重偏小，不符合实际工程情况。而当k值逐渐增大后，塑性区的宽度逐渐过渡到合理的取值范围中。但根据图4也可发现，只有当巷道侧向支承压力的应力集中系数k达到8以上时，工作面前方塑性区宽度才大于2 m，而根据静水状态下圆形巷道周围的应力分布计算可知，巷道围岩的应力集中系数通常达不到这么高，这主要是由于为了简化推导，将回采巷道的影响简化为一个应力集中系数k，若只取巷道围岩的峰值应力集中系数来作为k值，会导致巷道的存在对于工作面前方塑性区宽度以及支承压力的影响程度偏小，计算结果也相对偏小。因此，在取k值时建议结合压力拱理论进行计算，比较符合本力学模型的求解。

根据图5可知，支承压力峰值大小与原岩荷载的比值（即应力集中系数）和巷道侧向支承压力集中系数k并不呈线性关系，这表明工作面前方的支承压力峰值并不是巷道的侧向支承压力与工作面的前支承压力分开计算后的简单叠加。此外，工作面前方的支承压力峰值的增长速率随巷道侧向支承压力的增大而增大，即受巷道侧向支承压力的影响较大。

3 结 论

（1）在顶板与工作面前方矿体相互作用的地基梁模型的基础上，考虑了回采巷道侧向支承压力的影响，推导出了相应的顶板位移公式。通过该顶板位移计算公式可计算工作面前方的支承压力和塑性区宽度。

（2）通过工程实例计算发现，在计算塑性区宽度和支承压力峰值时，不考虑巷道侧向支承压力的影响，会导致计算结果偏低，不符合实际情况，因此在估算工作面前方支承压力峰值时不应忽略回采巷道侧向支承压力的影响。。

（3）由于承压力峰值大小与原岩荷载q的比值（即应力集中系数）和回采巷道侧向支承压力集中系数k并不呈线性关系，表明在实际工程中进行工作面前方支承压力峰值估算时，不能将支承压力峰值视为工作面前峰值支承压力与巷道侧向峰值支承压力的简单叠加，而要综合考虑两者之间的联系。