Distributed MPC for Reconfigurable Architecture Systems via Alternating Direction Method of Multipliers
2021-06-18TingBaiShaoyuanLiandYuanyuanZou
Ting Bai, Shaoyuan Li,, and Yuanyuan Zou,
I. INTRODUCTION
IN the past few decades, the advanced distributed model predictive control (DMPC) has received significant attention in both academia and industry for its outstanding advantages of dealing with multiple input/state constraints,better fault tolerance capabilities and a lower computational load. For geographically or physically distributed systems,DMPC provides an effective tool for control by effectively coordinating the optimal decisions of different local controllers with a guaranteed global performance. To date,numerous achievements in the research of DMPC strategies have been reached under fixed distributed frameworks [1]–[7].However, along with the system scale expansion and the continual function improvement, various application demands for the system structure reconstruction have risen, which incurs the issue of reconfiguration control. For instance, some partial failures in distributed systems [8], [9] may trigger the fault isolation to avoid a further fault propagation. Another example is the function extension to existing systems [10],which may bring in the insertion of several new components to existent systems. In order to achieve a dependable and renewed system functionality, it is of vital importance to study how to perform an efficient distributed control in the reconfigured architecture while maintaining a satisfactory dynamic performance.
Indeed, reconfiguration control with non-fixed system architectures has become an essential capability [11], [12] for networked systems to adapt to various external environments and a switching control task. Nowadays, research on the highefficiency distributed reconfiguration control strategies is still lacking. In the existing study [13], a reconfigurable control scheme for decentralized systems was proposed, where the coupling changes between different subsystems were handled by resorting to robust control invariant sets. For distributed systems with strong couplings, [14] presented an iterative reconfiguration scheme to cope with the significant interactions among subsystems and a class of time-varying terminal sets was designed. Notwithstanding, most of the existing reconfiguration control methodologies are developed based on the assumption that every reconfigurable control signal can be obtained within each sampling time. That is to say, it is based on the assumption that each control period is shorter than each sampling period, and the elapsed time spent in calculating the reconfiguration control input can be ignored.However, the computation of the optimal reconfigurable control law is time consuming in substantial real-world applications (especially for large-scale MPC optimization problems with multiple constraints), and the calculation efficiency of local controllers directly affects the distributed coordination of reconfiguration control. For the sake of avoiding a serious trajectory deviation in the context of system architecture realignment, the quick response ability of every local controller is of particular importance in the distributed reconfiguration control design.
As is known, the alternating direction method of multipliers(ADMM) is a high-efficiency iterative algorithm, which was originally introduced by Gabay and Mercier [15] in the 1970s and is well suited to large-scale convex optimization problems arising in statistics, machine learning, and other related areas.ADMM blends the benefits of dual decomposition and augmented Lagrangian algorithms for the constrained optimization and provides improved convergence properties under very mild hypotheses [16]–[20]. More precisely, the major advantages of ADMM can be summarized as follows:1) in theory, the convergence of the algorithm can be guaranteed for any convex cost functions and constraints;2) in practice, the augmented Lagrangian term often speeds up the convergence and computation. Although the powerful ADMM has been widely applied to solving convex optimization problems in the field of statistics, there is little research on the combination of ADMM and the reconfigurable DMPC scheme [21] to improve the computation efficiency and dynamic performance of reconfiguration control.Motivated by these reasons, in this technical note, we aim at proposing an efficient DMPC reconfiguration control scheme based on the powerful ADMM algorithm for linear networked systems with reconfigurable architectures. First, the distributed reconfiguration control strategy is presented with the consideration of three typical scenarios on the changeable system architecture. Next, the reconfigured controller design method is proposed and the iterative formulas based on ADMM algorithm for addressing the reconfiguration optimization problem are derived. Finally, the efficiency of the developed reconfigurable DMPC scheme is verified on the level control of a benchmark four-tank system.
The rest of the paper is organized as follows. A formal problem formulation is provided in Section II. In Section III,we introduce the distributed reconfigurable control scheme,including the reconfiguration control strategy, the way of reconfigured controller redesign and the resolving procedure of the reconfiguration control problem based on ADMM algorithm. Section IV applies the proposed reconfigured control scheme to a four-tank system, followed by some concluding remarks in Section V.

II. PROBLEM FORMULATION
Consider a distributed LTI (linear time-invariant) system composed byMsubsystems which are interconnected with each other through states and inputs. The local subsystemSiunder a fixed system architecture is described as
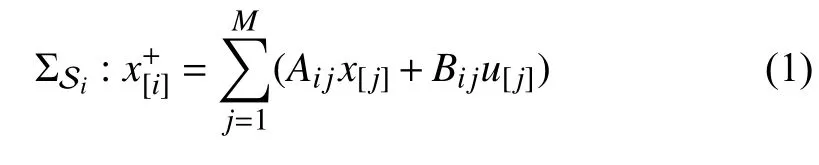

In the existing system architecture and control framework,we assume that the initial global system represented by(A,B)is controllable. Meanwhile, every local controller is designed according to the traditional non-cooperative DMPC strategy,i.e., a local performance index is minimized in determining the optimal control input. The initial DMPC optimization problem of subsystem Si,i∈M is expressed as


Fig. 1. Three typical reconfiguration scenarios. The red dotted lines denote the interconnections to be disconnected while the red solid lines represent the associated relationships to be newly established.

wherex[i](k+h|k),u[i](k+h|k) denote the values ofx[i]andu[i]at the future time (k+h) predicted at the timek. The terminal invariant set Xifis devised with guaranteed stability of the global system in the existing system structure.
Throughout this context, the communication protocol in controller design is provided by the following assumption.
Assumption 1:The communication between two interconnected local subsystems Siand Sjis permitted if and only ifi∈Pjori∈Cj.In line with different reconfiguration demands in real applications, we focus on three typical reconfigurable scenarios in this paper: inserting new subsystems,disconnecting existing subsystems, and modifying the couplings between different local subsystems. As described earlier, inserting several new subsystems generally maps the requirement of system function extension, troubleshooting or subsystem recovery. Disconnecting existing subsystems often corresponds to failure isolation; modifying the couplings between interconnected subsystems arises from the need of system structure improvement. A more clear illustration to the three typical reconfiguration scenarios is given by Fig. 1. Note that the three scenarios cover the basic reconfiguration modes in a distributed system framework, and other complicated reconfigurable architecture requirements can be viewed as a combination of them.
In the sequel, we propose to investigate the DMPC reconfiguration control scheme by employing the powerful ADMM algorithm with respect to the above three typical reconfiguration scenarios. It is attributed to achieving a quick control response capability and a satisfactory dynamic performance in the reconfigurable distributed control.
III. RECONFIGURATION CONTROL SCHEME
This section introduces the DMPC reconfiguration control scheme for linear systems with reconfigurable architectures.Specifically, in the first place, the reconfiguration control strategy in terms of three typical reconfiguration scenarios is presented. Secondly, we show how to redesign the local controllers for some selected subsystems in the reconfigured control. Then, the way to resolve the reconfiguration optimization problem via the powerful ADMM algorithm is provided, which equips local subsystems with a quickresponse ability to dynamical structure changes and helps to achieve a good distributed coordination during the whole reconfiguration control.
A. Distributed Reconfiguration Strategy
Due to the realignment of system architectures, the dynamics and interconnections of partial local subsystems are changed compared with those in the original system architecture. Here, we first provide a detailed analysis to the influence of three typical reconfiguration scenarios to every local subsystem. Later, the reconfiguration control strategy is presented accordingly.
First, in the renewed system architecture,AreandBreare utilized to represent the reconfigured system matrix and input matrix, respectively. Then, the dynamics of the reconfigured global system can be described as


Next, aiming at three typical reconfiguration scenarios, a reconfiguration strategy is proposed which determines the local subsystems whose controllers need to be redesigned in the further reconfigured control. In order to minimize changes to the existing controller designs while realizing an effective control of the global reconfigured system, the directly influenced subsystems are selected to re-conceive their local controllers. Specifically, taking into account the structure modification by means of subsystems removal, subsystems addition or coupling realignments between different subsystems, the directly influenced subsystems are referred to as the subsystems whose reconfigured subsystem dynamics is different from the original subsystem dynamics in the initial system architecture. By (1) and (6), the set of directly influenced subsystems R is determined by

B. Reconfigurable Controller Redesign


To equip live systems with a rapid response ability to various reconfiguration requirements and then achieve a good distributed coordination, we next provide an approach to transform the reconfigurable control problem (8) into a standard optimization formulation for employing the ADMM algorithm.


C. Solution of the Reconfigured Control via ADMM
Hereafter, the method for solving the reconfigured optimization problem (9) by resorting to the powerful ADMM algorithm is proposed. Generally, the constrained DMPC problem can be addressed by employing the fmincon function in Matlab if the available calculation time is sufficient. For many cases of the instant structure reconfiguration requirements, such as the isolation of several failed subsystems to prevent a further fault propagation, the time to prepare the reconfiguration control is quite limited.Furthermore, the slower the reconfiguration control response,the harder it is to achieve a satisfactory distributed coordination and the greater the system state deviation in the renewed system architecture. For these reasons, below we intend to solve the reconfigured DMPC problem (9) via the high-efficiency ADMM algorithm, which helps to significantly improve the computational efficiency of the reconfigured control response and then achieve a satisfactory reconfiguration control property.
First, taking into account the general form of ADMM in solving optimization problems

For the above general form of ADMM, the optimization problem (10a) is solvable in the precondition of the following two assumptions [22], which are used to guarantee the existence ofxandzthat can minimize the augmented Lagrangian function.
Assumption 4:The functionsf(x) andg(z) are closed,proper and convex.
Assumption 5:For simple Lagrangian


On this basis, we aim to derive the iterative formulas that can be applied to solving the proposed reconfiguration control problem. In line with the general form of (10a) and (10b), the reconfigured DMPC optimization problem (9) can be redescribed as the following form

Similarly, by minimizing (12a), we can obtain that

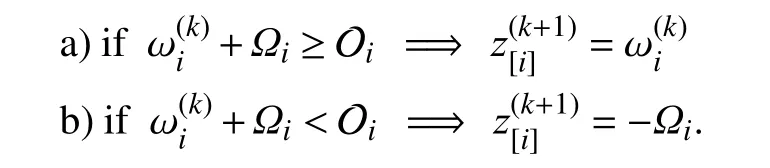
As a result, the iterative formulas to solve the reconfigurable DMPC optimization problem (12) via the powerful ADMM algorithm are obtained as

Meanwhile, as the iteration proceeds, the reasonable termination criterion is designed by


Additionally, the thresholds of the primal residual ϵpriand the dual residual ϵdualare respectively designed as

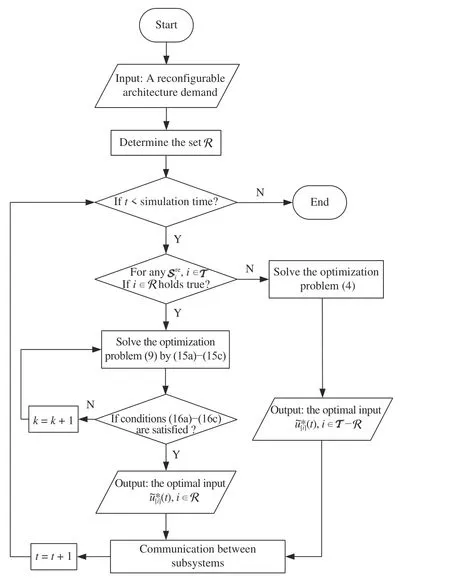
Fig. 2. An algorithm flow chart of the proposed reconfiguration control scheme.
IV. AN ACADEMIC EXAMPLE
This section verifies the effectiveness of the proposed reconfiguration control scheme on the level control problem of a benchmark four-tank system [23]. The multi-variable laboratory plant is composed by four interconnected tanks with nonlinear dynamics and is subject to both state and input constraints. There are two inputs (i.e., pump throughputs)which can be used in controlling the tank levels. A schematic of the process for the four-tank system in the existing architecture is shown in Fig. 3. The water in bottom reservoir is transfered by the pumpsqaandqbto the upper tanks and the liquid levels of each tank can be measured by the local pressure sensors.
To proceed, the state space continuous-time model of the existing four-tank plant is described by the following equations
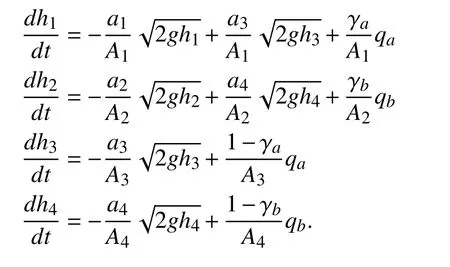
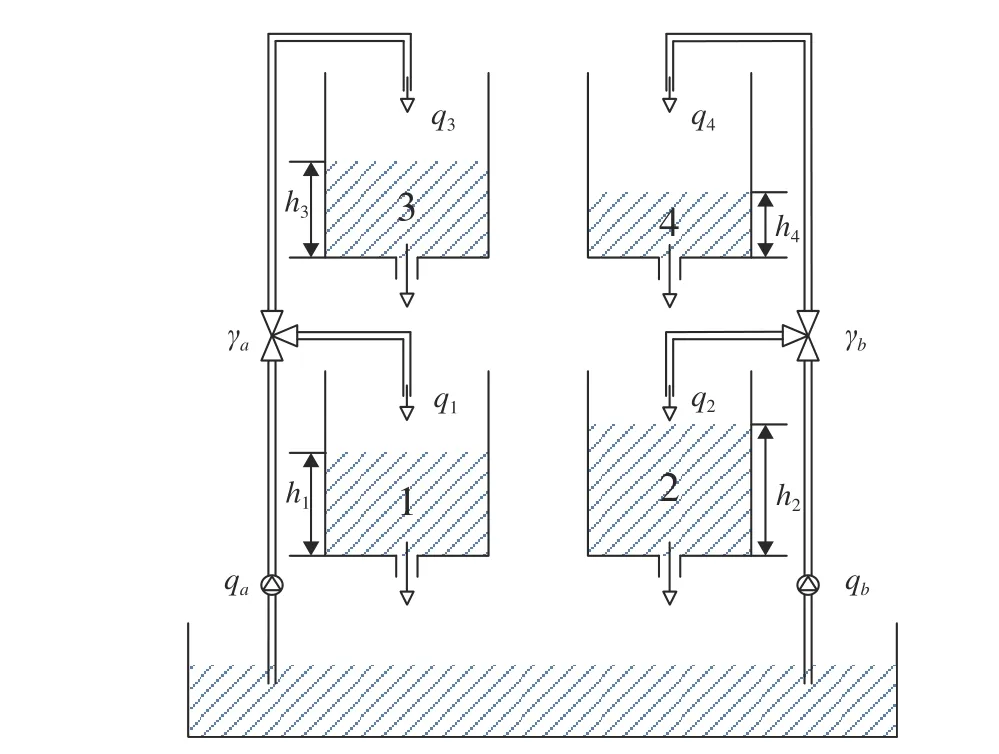
Fig. 3. A schematic description of the exiting four-tank system.
In this example, the water level of each tank is constrained byhi∈[0.2,1.6], ∀i∈{1,2} andhi∈[0.2,1.3], ∀i∈{3,4},where the minimum level is used to prevent eddy effects in discharge of the tank. Meanwhile, the flow of pumpaandbare confined byqa∈[0,3.26] andqb∈[0,4]. The detailed nominal operating conditions and the parameters estimated on the real four-tank system are provided in Table I.

TABLE I THE NOMINAL OPERATING CONDITIONS AND THE PARAMETER VALUES OF THE FOUR-TANK SYSTEM

where τidenotes the time constant of each tank. The control objective of the four-tank system is to keep the levels of every tank at the specified reference values. In the existing system architecture, as shown in Fig. 2, the global system is divided into two subsystems withx[1]=[x1;x3],u[1]=u1andx[2]=[x2;x4],u[2]=u2. The two discretization subsystem models are expressed as
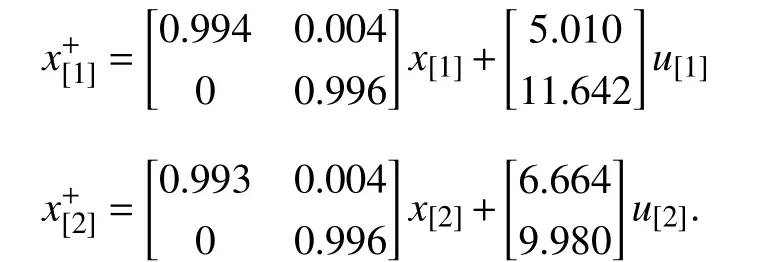
To verify the presented reconfiguration control scheme, we modify the existing system architecture in Fig. 3 into the system structure shown in Fig. 4, where another branch from pumpais connected to tank 4 while a new branch from pumpbbecomes an input for tank 3.

Fig. 4. The plant schema of the reconfigured four-tank system.
In the renewed distributed system architecture, the reconfigured discrete-time subsystem models are given below.

The prediction horizon is selected asN=5. In the reconfigured controller design based on the ADMM algorithm, the over-relaxation parameter α(k)=1.8 and ρ=0.2.Meanwhile, the state and input weighting matrices are

The simulation results of the reconfiguration control in Case I are shown in Figs. 5 and 6. More precisely, Fig. 5 shows the dynamic performance of local subsystems without using the reconfiguration control scheme. During the control process of 0–2 00 steps, the system is controlled by initial controllers in the original system architecture. At iteration 200, the system structure changes in line with the architecture shown in Fig. 4.Similarly, in Case II, the simulation results are shown in Figs. 7 and 8, where the system architecture is modified at iteration 400. As can be seen from Figs. 5 and 7, the system dynamics in the existing controller design tends to be oscillating and divergent after the structure reconfiguration due to the strong input couplings between subsystems.
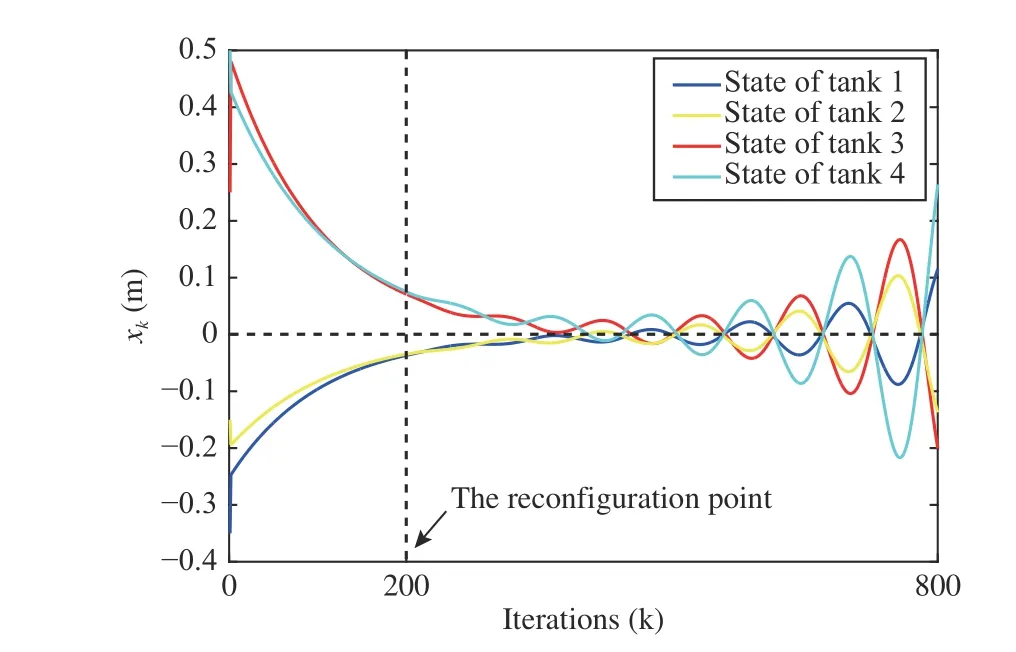
Fig. 5. System performance in the existing controller design in Case I.

Fig. 6. System performance in the proposed reconfiguration control scheme in Case I.
For comparison, the control performance of the proposed reconfigurable DMPC scheme via the ADMM algorithm in both Cases I and II are depicted in Figs. 6 and 8. As is shown,although a small fluctuation appears at the reconfiguration point, the global system state converges to the steady point in a short period of time, which illustrates the effectiveness of the presented reconfiguration control scheme.

Fig. 7. System performance in the existing controller design in Case II.
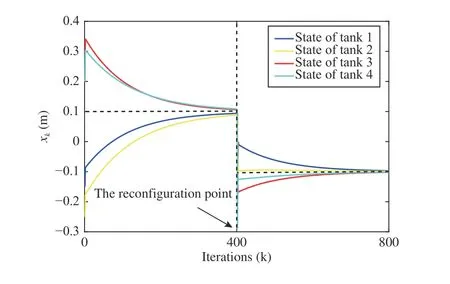
Fig. 8. System performance in the proposed reconfiguration control scheme in Case II.
Moreover, to illustrate the high efficiency of the proposed reconfigured control method combined with the ADMM algorithm, the time consumed in calculating the optimal reconfigured DMPC input via the traditional fmincon function(RDMPC(fmincon)) and the powerful ADMM (RDMPC(ADMM)) are compared. As is shown in Table II, the mean computational time in each iteration with using fmincon and ADMM are 0.145 s and 0.005 s, respectively. During the600 iterations, the comparison of the accumulated computation time is shown in Fig. 9. From these results we can see that, the calculation efficiency via ADMM is greatly improved in computing the optimal reconfigured input, which helps to ensure a quick-response ability and a satisfactory dynamic performance in the reconfiguration control.

TABLE II COMPARISON OF THE TIME CONSUMED IN SOLVING RDMPC VIA FMINCON AND ADMM
V. CONCLUSION

Fig. 9. Comparison of the accumulated computation time in solving the RDMPC via fmincon and ADMM.
This paper proposed a novel reconfiguration DMPC scheme for linear systems combined with the high-efficiency ADMM algorithm. First, taking into account three typical scenarios, a distributed reconfiguration control strategy applying to any reconfigurable requirements was presented. Secondly, based on the powerful ADMM algorithm, the way to redesign the reconfigured DMPC controller was provided and the iterative formulas employed in solving the reconfiguration optimization problem via ADMM algorithm were derived.Finally, the proposed reconfiguration control method was applied to a benchmark four-tank system to illustrate its higher efficiency and good reconfigured control performance.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- A Fully Distributed Approach to Optimal Energy Scheduling of Users and Generators Considering a Novel Combined Neurodynamic Algorithm in Smart Grid
- A Survey and Tutorial of EEG-Based Brain Monitoring for Driver State Analysis
- Global-Attention-Based Neural Networks for Vision Language Intelligence
- Towards Collaborative Robotics in Top View Surveillance: A Framework for Multiple Object Tracking by Detection Using Deep Learning
- Lightweight Image Super-Resolution via Weighted Multi-Scale Residual Network
- Human-Swarm-Teaming Transparency and Trust Architecture
