含偶氮苯聚合物线性偏振全息光栅的物理特性

吴洋，邢美术，林兆培，丁亚茜，张明

(1.中国电子科技集团公司 第二十三研究所，上海 201900；2.兰州交通大学 电子与信息工程学院，甘肃 兰州 730070)

0 引 言

现代信息技术是以计算机和通信技术为核心，对信息进行收集、存储、处理、传输或显示的高科技技术。在众多信息存储和处理技术中，光信息处理技术以其存储容量大、数据传输速率高等优点，在众多技术中脱颖而出。偏振全息作为光信息处理技术中的一种，具有实现全光逻辑操作、高密度光存储以及制备分布反馈式激光器等特点，成为近几年研究的热点[1-8]。

与传统全息相比，偏振全息可通过对记录光和信号光偏振度的调制，进而控制衍射光束的偏振态和能量，利用该特性制作折射率周期性变化和衍射光偏振度可控的空间相位光栅；同时，其理论衍射效率在薄膜中可达100%，远优于传统全息。偏振全息光栅一般在非线性光学材料中构建，近年来，有关光折变晶体，液晶材料，光致聚合物，纳米颗粒复合薄膜和光致色变染料掺杂聚合物的全息记录的动力学研究结果被大量报道，然而，关于形成偏振全息光栅的理论研究却不够深入[9-15]。

本文通过Jones矩阵推导正交线性偏振全息光栅的传输矩阵，以及零阶和一阶衍射光的输出矩阵。线性偏振全息的传输矩阵为空间周期性调制，其衍射信号的传输方向和信号强度可由传输矩阵的傅里叶变换求得，理论公式表明其一阶衍射率可达到50%，衍射信号的偏振度由记录光和信号光的偏振度共同决定。结合实验利用Pump-probe法分析了含偶氮苯的本体聚合物在两个正交线性偏振光的照射下，其零阶和一阶衍射光之间的能量转换规律。

1 正交线性偏振全息光栅的传输矩阵及衍射光

如图1所示，入射记录光R和信号光S分别为垂直和水平偏振，则R和S为一组正交线性偏振光。记录光和信号光以z轴为中心以-θ和θ角垂直入射到本体材料x′——z面上。假设入射光ER和ES有同样的光强I1=I2=A2/2，则ER和ES可用Jones矢量表示为

(1)

式中，δ=2πsinθx′/λ。在此条件下，其干涉场为

(2)

从式(2)可以看出,当两束入射光光强相同时，并没有对信号强度进行调制(光强为常数)，只对偏振态进行了调制。

式(2)中，当δ=0,π/2,π,3π/2…时，干涉波为线性偏振。当δ=0时，由于cos 0=1，sin 0=0，所以干涉波在x轴上为线性偏振。当δ=π/2时，在y轴上为线性偏振。当δ=π/4时，干涉场可写为

(3)

干涉波为左圆偏振光(LCP)。而当δ=3π/4或δ=7π/4时，为右圆偏振光(RCP)。由此可知，干涉波偏振调制的形状仅与入射光ER和ES间的相位差2δ有关。其偏振模式如图2所示。

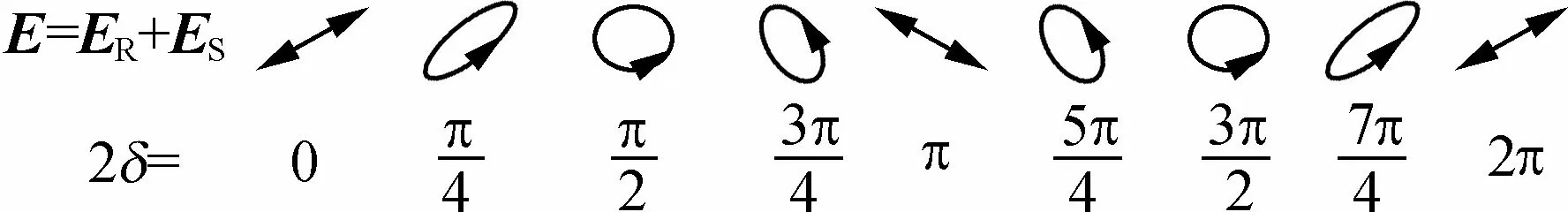
图2 当ER和ES分别为垂直偏振和水平偏振时的极化模式

通过式(2)可得到3项Stokes参数[16]：

S0=1,

S1=cos (2δ),

S2=0，

(4)

此光场场强为常数，记为仅记录几何图形的纯偏振全息，其无信号调制且与入射记录角θ无关。

当材料由干涉场而引起光致双折射时，偏振全息光栅会由双折射的周期性调制形成。利用Stokes参数，在x-y坐标系下全息光栅的传输矩阵可描述为

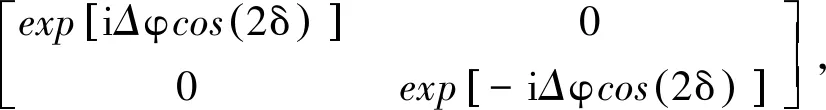
(5)

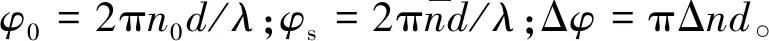
T=T0+T1+T2+…,

(6)

其中,T0，T1和T2分别为

T0=T0(Δφ),

(7)

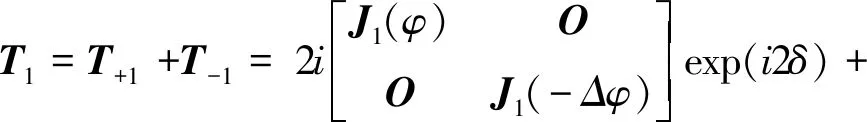
(8)

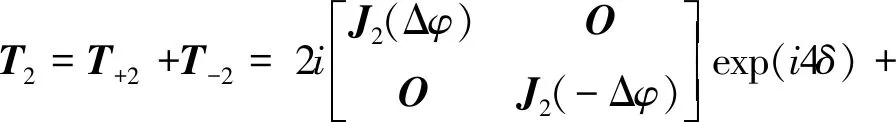
(9)

用探测光的Jones矢量Ep(|E|p=A2)乘以传输矩阵T，可得衍射光的Jones矢量。使探测光为线性偏振，偏振方向与x轴的夹角为γ，且如图1所示沿着E1的传输方向传输。则探测光Ep可表示为

(10)

零阶光与探测光同为线性偏振光且偏振方向一致，其振幅为Ip(J0(Δφ))2。±1阶光的振幅为

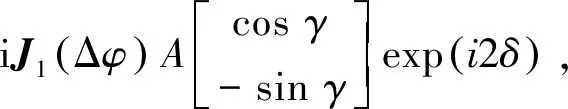
(11)

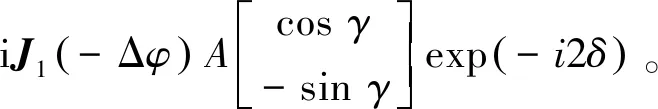
(12)

衍射光E+1和E-1为线性偏振光且偏振角为-γ，这意味着基于探测光，衍射光移动了2γ。如果探测光Ep的偏振角γ=45°，则一阶和三阶衍射光均为圆偏光。一阶衍射光的强度可用一阶贝塞尔函数表示为

I+1=I-1=Ip(J1(Δφ))2。

(13)

当探测光Ep为左圆偏振时，可记作

(14)

一阶衍射光为

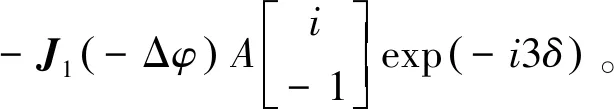
(16)

一阶衍射光E+1和E-1均为右圆偏振，其信号强度可表示为一阶第一类贝塞尔函数的平方,即

I+1=I-1=Ip(J1(Δφ))2。

(17)

2 实 验

使用的聚合物材料为掺偶氮散料分散橙3(4-(4-nitrophenylazo)aniline，Disperse Orange 3,DO3，90% dye content)和聚甲基丙烯酸甲酯(poly(methyl methacaylate),PMMA,MW=15 000)。材料均从Aldrich购买，未做任何处理。掺杂质量分数为10%，厚度为1 cm。最后将本体聚合物置于70 ℃的恒温箱8 h，去除残留溶剂。

衍射测量实验光路图如图3所示。由于样品较厚，因此在采用Pump-probe方法测量衍射率时，记录光和信号光均采用波长633 nm的氦氖激光器。首先通过偏振片将激光调制为水平偏振光(P)，分束器BS2确保了记录光ER和信号光ES的初始偏振度一致，调节半波片W1，使2δ=π，ES为垂直偏振光(S)，满足式(1)条件，即ER和ES为一组正交线性偏振光。中性灰度镜ND1衰减ER的光强，使ER和ES的光强相同，确保没有对信号强度进行调制。当探测光为P光时，不需要经过1/4波片W2,直接入射至样品。当探测光为LCP时，调节W2，使2δ=π/2，探测光的干涉场如式(3)所述。记录光的光强固定为8 mW/cm2，同理在斩波器后加入ND2，以保证探测光的光强远小于记录光和信号光，使信号光对光栅不造成影响，信号光的光强固定为0.5 mW/cm2。同时采用锁相放大器(SRS SR510)去除外界噪声，机械斩波器的调制频率固定为300 Hz。所有实验均在室温条件下进行。光路图中器件缩写如下：P-偏振片；BS1，BS2-分束器；ND1，ND2-中性灰度镜；W1，W3-半波片；W2-1/4波片；M1，M2-反光镜；PMT-光电倍增管。

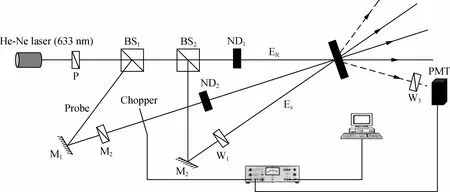
图3 衍射测量光路图

3 结果及讨论

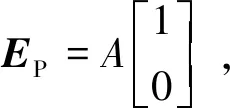
当探测光为左圆偏振(LCP)时(图4(b))，其一阶衍射光的信号强度如式(17)所示，可表示为一阶第一类贝塞尔函数的平方，因此，其衍射率变化趋势与探测光为P光时相似。当打开记录光后，零阶衍射效率从100%开始下降，在1 250 s处降为0；一阶衍射效率随时间上升，在950 s左右升至33%。能量在二者之间周期性地互相转移。由实验结果可知，当样品在一组正交线性偏振光照射下，其衍射效率与探测光的偏振态无关。目前薄膜光栅的衍射率一般为5%～10%，当样品厚度增至1cm时，衍射率可高达到30%以上，得到了显著提升。由图4可看出，实验结果与理论有较高的拟合度，即衍射效率的变化趋势符合一阶第一类贝塞尔函数的平方，证明了理论推导的正确性。

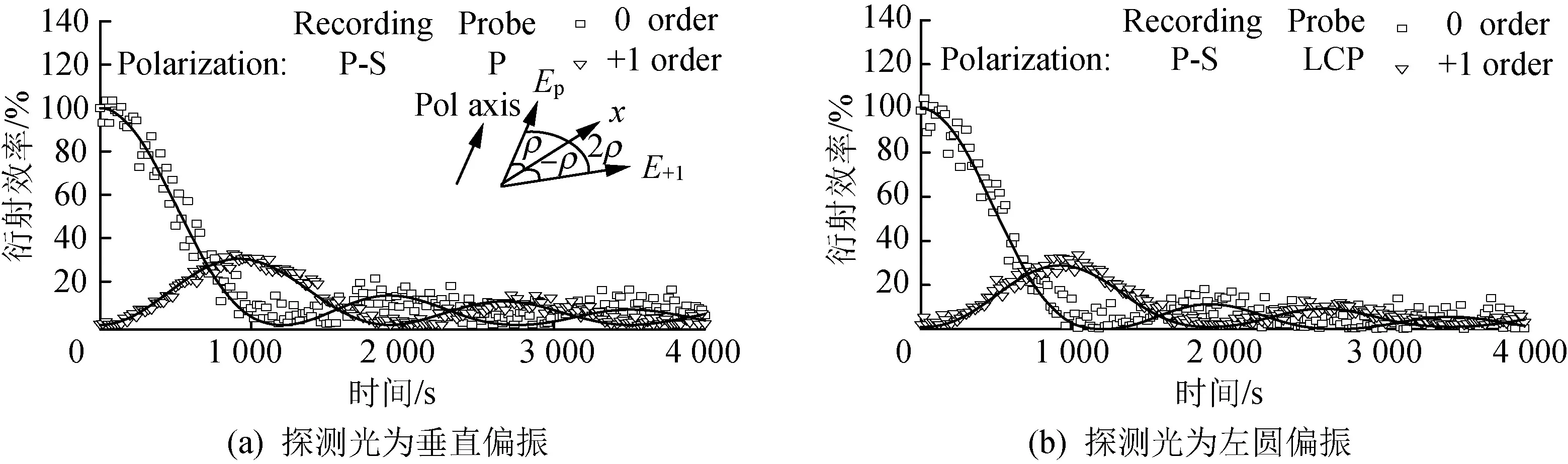
图4 样品的零阶和一阶衍射效率

当垂直偏振的探测光(S)垂直照射在本体聚合物上时，由式(11)可知，+1端的衍射光也为垂直偏振。为了得到信号光偏振方向与一阶衍射效率的关系，做如下实验：在固定记录波偏振方向的前提下，为了监测探测光偏振方向与一阶衍射效率的关系，在探测光端放置一个半波片W2，用以控制探测光的偏振方向，同时在PMT前放置一个与探测光初始偏振方向相同的偏振片W3，以过滤不同偏振方向的衍射光。

图5为聚合物在正交线性偏振记录光(P-S)照射下，在探测光的线性偏振角发生变化时，其一阶两个衍射光衍射效率的变化规律。当探测光垂直入射至聚合物表面的偏振角为γ时，由式(11)和(12)可知，衍射光的偏振角也为γ，信号强度为cos2(2γ)的函数。由实验结果可看出，当2γ=45°,135°时，一阶衍射光的衍射率最低，其峰值出现在2γ=90°处。这表明当信号光的偏振角转动γ时，一阶衍射光的偏振角转动了2γ。即当探测光为垂直偏振时(γ=45°)，衍射光为水平偏振(P)。

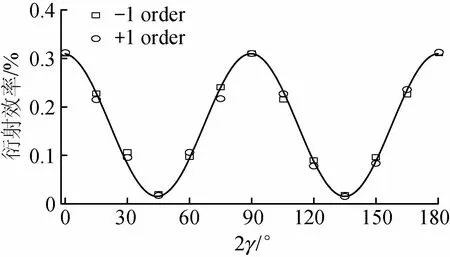
图5 ±1阶衍身光的衍射效率为偏振角2γ的函数

4 结 论

本文研究了含偶氮苯本体聚合物的线性偏振全息光栅形成机理及物理特性，通过琼斯矩阵推导了光致各向异性引起的线性偏振全息光栅的理论方程。传输矩阵T周期性地对幅度进行空间调制，通过对T进行傅里叶变换得到衍射波的传输方向和信号强度，理论公式表明其一阶衍射率可达到50%。在两束正交的线性偏振记录光照射下，其零阶和一阶衍射效率均发生周期性变化，其时域变化趋势符合一阶第一类贝塞尔函数的平方。衍射光能量在零阶和一阶衍射光之间不停传递。当厚度为1 cm的样品在两个正交线性偏振光的照射下，探测光为线性偏振时，其+1端衍射光的最大衍射效率为32%；当探测光为左圆偏振时，+1端衍射光的最大衍射效率为33%。实验结果表明当记录光和信号光为一组正交的线性偏振光时，衍射光的衍射效率与探测光的偏振态无关，与理论相符。当探测光的偏振角转动γ时，一阶衍射光的信号强度为cos2(2γ)的函数。