基于压缩感知的超分辨率重建研究综述
2021-06-18李莹华乔杨歌王富平
李莹华,乔杨歌,刘 颖,3,卢 津,王富平
(1.西安邮电大学 电子信息现场勘验应用技术公安部重点实验室,陕西 西安 710121;2.西安邮电大学 图像与信息处理研究所,陕西 西安 710121;3.西安邮电大学 陕西省无线通信与信息处理技术国际合作研究中心,陕西 西安 710121)
随着移动通信和互联网技术的快速发展,单纯的文字和语音通信已经难以满足生活等应用需求。图像视频能够传递更丰富的信息,现已成为主要通信形式之一。在图像处理中,接收图像和视频的高质量恢复技术在很多领域有着至关重要的作用,如医学成像、遥感图像、卫星图像、高清电视、远程医疗、监控视频、视频会议,以及人们日常生活中必不可少的手机等智能设备对图像的存储传输。
图像有与语音文本截然不同的特点,包含数据量巨大,内部结构具有高相关性。采集图像的传感器尺寸等硬件限制,或者采集场景中的天气原因、光照和气流等自然干扰,以及图像量化、模数转换等造成的图像失真、分辨率降低等问题,导致图像的细节信息丢失,从而不能进行很好的应用。因此,如何在接收端高效重构高质量的图像是图像处理和多媒体通信中至关重要的问题。
一般来说,提升图像清晰度和分辨率主要可以从硬件和软件两种方法实现。硬件方法主要是提高传感器的工艺,成本高且较难实现。软件方法主要是通过计算机视觉,对图像进行超分辨率(Super-Resolution,SR)重建,通过对低分辨率(Low Resolution,LR)图像的处理,利用机器学习、概率统计理论和优化理论等工具可重构出低分辨率图像对应的高分辨率(High Resolution,HR)图像。软件方法较硬件方法成本低,方法也多样化,能够自适应地对不同类型的图像SR 进行改进,更易于实现,因而这种软件化的超分辨率更加实用。目前,超分辨率主要的重建方法有基于插值法的SR、基于重建的 SR 以及基于学习的SR等3类。其中,双线性插值法(Bicubic)[3]是最典型的插值法,实现简单,但重建图像质量较差;基于重建的SR 方法主要缺点是对加性噪声的鲁棒性较差;基于学习的SR方法主要有邻域嵌入方法、支持向量回归(Support Vector Regression,SVR)方法以及利用图形patch 的稀疏表示实现超分辨率,虽然能够恢复出较为细致的纹理,但是因为很多高频信息是通过外部训练库学习的,结果图中可能会存在不真实的细节。超分辨率重建是一个典型的病态问题,由于没有足够的低分辨率图像用于重构,同时降质模型未知,且根据约束条件求得的解也不是唯一的,因此,上述方法均存在运算复杂度低或者重建图像质量不理想等问题。为解决这些问题,引入了基于压缩感知理论的超分方法。压缩感知(Compressed Sensing,CS)的出现为解决大的欠定问题提供了新的不同视角。在没有关于信号支持的先验知识的情况下,CS可以使用比传统方法更少的测量重建稀疏或可压缩信号。
通过介绍基于压缩感知理论的超分辨率重建研究的发展状况,对比分析几种典型的基于压缩感知的超分辨率方法,并展望图像超分辨率未来的研究方向。
1 超分辨率相关概念
1.1 图像降质模型
采集图像过程就是真实场景图像的一个降低信息的过程,采用计算机视觉的方法,可实现对高分辨率图像的恢复,图像制作对应的降质模型如图1所示。图像分辨率的降低是空间上高频信号丢失所导致的,光学系统可以看作是一个空间上的低通滤波器,只能允许一定带宽范围内的空间频率信号通过。在实际的图像采集和传输中,有许多因素会造成图像的降质,导致图像分辨率的下降。就采集图像的设备来说,传感器尺寸、不同的镜头以及不同的互补金属氧化物半导体(Complementary Metal Oxide Semiconductor,CMOS)质量都会影响图片的质量。如卫星图像以及监控视频,传感器的尺寸小,光通量也相应减小,导致了分辨率的降低。另一方面,即使传感器能够采集到高分辨率图像,采集场景以及设备的相对运动都可能会造成成像时产生畸变。随着对图像质量的要求越来越高,硬件无法自适应地采集高精图图像,并且配置高精度光学仪器和传感器的价格昂贵,性价比并不高。因此,通过改进硬件条件难以达到所有图像处理应用领域的需求。

图1 图像降质模型
1.2 超分辨率的主要重建方法
超分辨率理论是由Tsai[1]等人在上世纪末提出的。最初的超分辨率技术主要应用于卫星图像领域,根据卫星在同一场景下采集的多幅图像重建出高分辨率图像,再获取需要的细节信息。这种技术需要多幅图像的输入,限制较多,因此,后来很多学者开始致力于研究单幅图像的超分重建。超分辨率的主要重建方法包括基于插值法的SR、基于重建的SR和基于学习的SR等3类。
1)基于插值法的SR。插值法[2-5]是先根据已有的低分辨率图像之间的相对运动信息,在已有采样值的基础上,计算出高分辨率图像在非均匀采样点上的像素值,然后在非均匀采样点上进行插值并估计每个高分栅格上的像素值,最后进行去模糊和去噪处理。典型的邻插值方式有近邻插值法、双线性插值法和B样条插值法,其优点是计算复杂度低,实现容易。然而,该方法的前提条件是假设要求所有低分辨率图像的噪声与模糊相同。此外,得到的图像过于平滑,丢失了细节纹理信息,又没有加入先验信息,在重建HR图像的细节信息时会遭遇瓶颈。
2)基于重建的SR。重建的SR主要是通过建立数学模型模拟从原高分辨率图像到低分辨率图像的降质模型,即是一个典型的欠定问题,利用正则化解决此逆问题是基于重建方法常用的方式。典型的重建方法有迭代反投影(Iterative Back Projection,IBP)和凸集投影(Projection onto Convex Set,POCS)等方法[6-9]。这类方法的缺点是对加性噪声的鲁棒性较差。
3)基于学习的SR。该方法主要是从大量的训练样本中获取先验信息,建立低分与高分图像的特征空间的映射关系,通过得出他们之间的对应关系,对感兴趣的LR图像学习得出的映射关系进行恢复。利用邻域嵌入方法[10]、支持向量回归方法(Support Vector Regression,SVR)以及图形patch 的稀疏表示实现超分辨率[11]时,很多高频信息是由外部训练库学习得到,虽然恢复了较为细致的纹理,但是结果图中可能会存在不真实的细节。目前,基于学习的方法已有较多研究,但是针对不同的应用,基于插值的方法和基于重构的方法也有其自身的优点,仍然被很多学者所重视。
2 基于压缩感知的超分辨率重建
2.1 压缩感知理论
在传统的信号处理中,先根据奈奎斯特(Nyquist)采样定理对信号进行高速采样,对采样值进行数字化处理和频域变换后,对频域分布上较重要的系数进行编码,再对编码值进行存储和传输。随着多媒体网络的发展,现在需要处理的都是具有大数据量大维度的图像和视频信号,在带宽资源受限的应用环境下,已有的硬件设备很难满足高采样率进行采样压缩的要求,并且先采样再压缩的过程会导致大量存储资源的浪费和采样值的冗余。在此背景下,信号处理领域的学者们开始探寻能够将压缩和采样同步进行的解决办法,压缩感知(Compressed Sensing,CS)理论相继被提出。
CS理论可以远低于Nyquist的采样率同时实现对信号的采样和压缩。需要说明的是,CS 理论研究的出发点是克服Nyquist采样要求的限制,因此, CS理论与Nyquist采样定理存在3点区别[12]。第一,Nyquist采样定理针对的对象是无限长的连续信号,而CS理论关注的则是有限维观测空间的向量。第二,Nyquist 采样定理是对信号进行均匀采样,而CS理论则是通过一个随机测量矩阵,与信号求內积获得测量值。第三,传统的信号采样压缩传输后,其信号的恢复是通过对采样数据的Sinc 函数进行线性插值获得,而CS理论中则是根据测量值,求解一个欠定的凸优化问题恢复出信号。
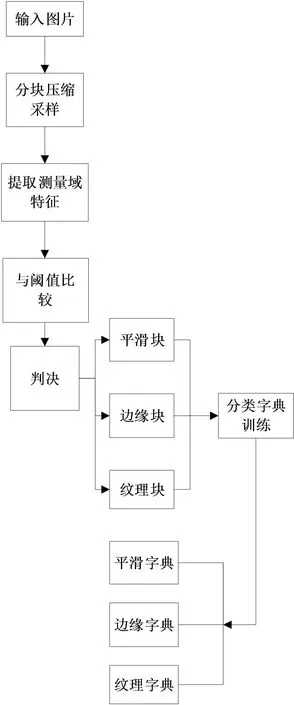
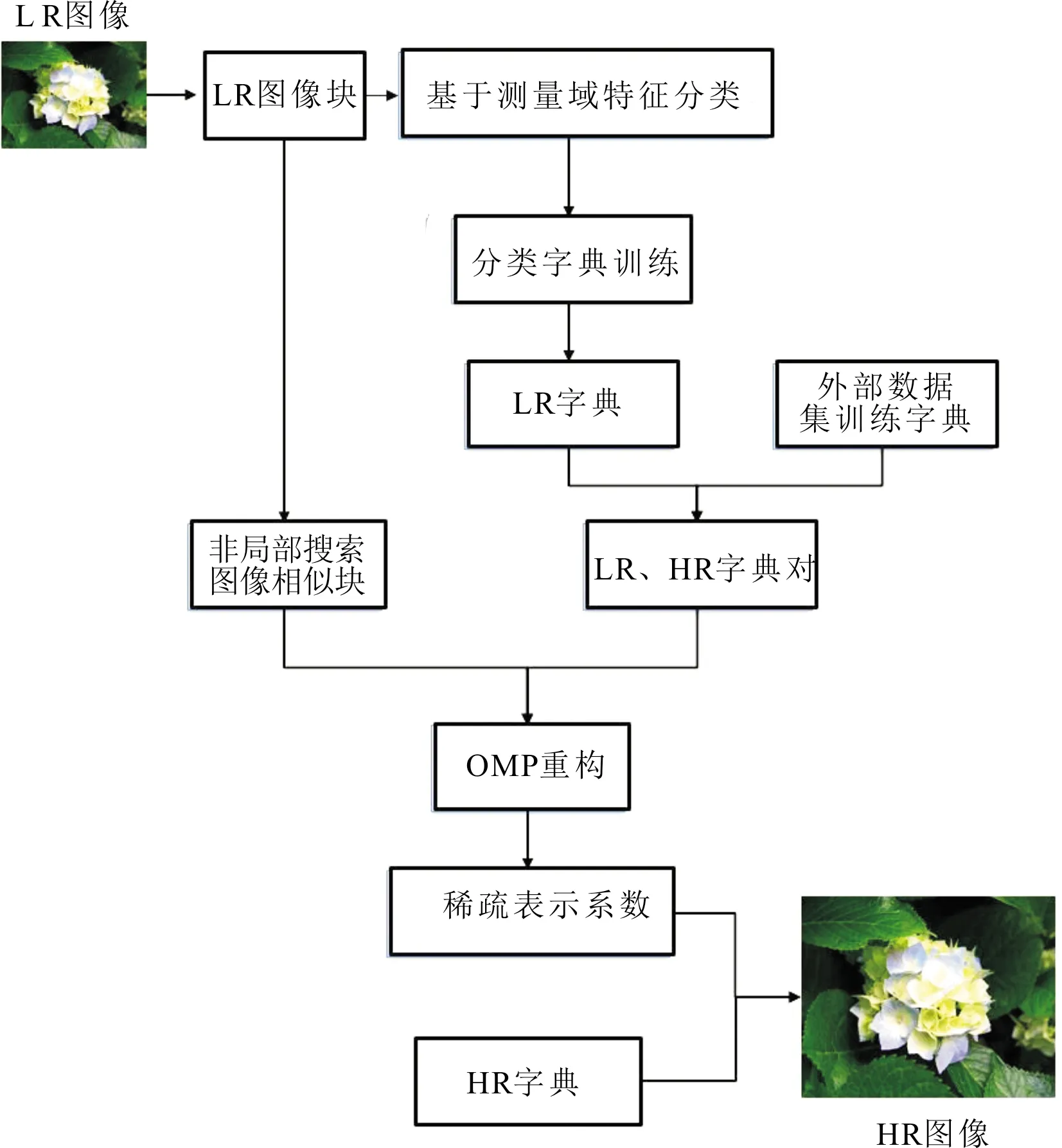
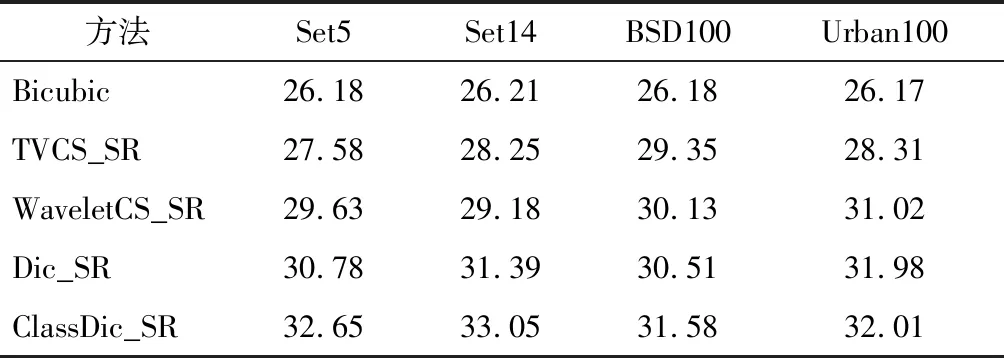
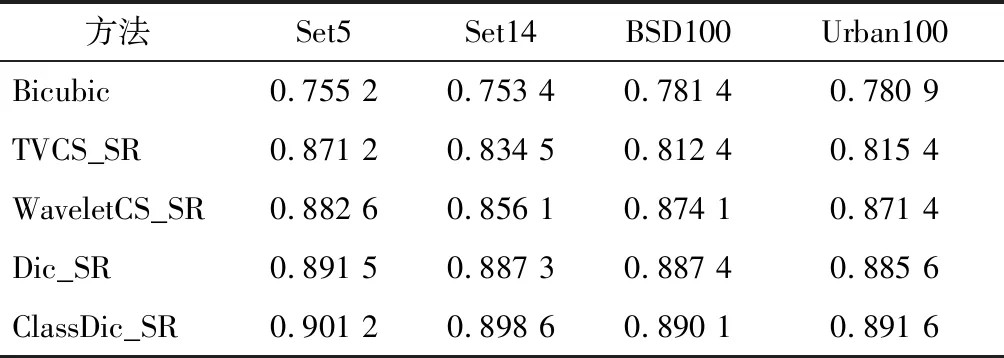
压缩感知可以用远少于传统方法的测量值恢复出稀疏或者可压缩的信号[13-15],CS理论的出现影响了信号采集和恢复。假设x是一个N维的离散信号,若其元素的非零值个数不大于r(r< ‖x‖0≤r,⟹x是r-稀疏信号 同时,若某一信号的幅度值呈指数型衰减,则称该信号为“近似稀疏信号”。此外,若一个信号在某一个表示基上具有近似稀疏的表示系数,则称该信号为“可压缩”信号。 对于自然图像来说,包含的像素一般都有较强的相关性,不满足严格意义上的稀疏性。但是,可以找到合适的稀疏基对图像进行表示,而稀疏表示系数是满足稀疏性的,故图像是可压缩信号,可以利用CS理论对自然图像进行处理。信号压缩感知的过程如图2所示。 图2 信号压缩感知的过程 对于N维离散信号x(x∈RN),{ψi}(i=1,2,…,N)是Ω∈RN空间的一组正交基,将x在这组正交基下展开,即 (1) x=Ψα (2) 其中,α是信号x的稀疏度。在CS理论中,稀疏基的构造称之为稀疏字典的设计。按照字典的构成方式,稀疏字典可以分为正交基字典、基于框架构造的字典和基于学习的字典。从正交性角度来分,又可分为正交基和过完备冗余字典。稀疏字典的设计是至关重要的部分,因为信号在字典上的表示系数的稀疏程度决定了重构图像的精度。 利用M×N(M≪N)维的测量矩阵Φ对信号x进行测量,则有 y=Φx (3) 式中,y∈RM表示经测量矩阵观测后的M维测量值信号。将M/N称作压缩感知中对信号进行测量的采样率,记为符号MR(Measurement Rate)。 对信号的测量过程也可看作是原信号根据测量矩阵从高维空间到低维空间的降维投影过程。测量值的每个元素均是原信号分量的加权和,因而每个测量值均包含了部分原信号所有分量的信息。利用CS理论对信号进行测量,彩色图块分别表示信号和测量矩阵的元素,则测量过程可用色块矩阵表示,如图3所示。 图3 压缩感知的测量过程 在解码端根据测量值对信号进行精确重构,需从测量值y∈RM中重构出原始信号x∈RN。由于M≪N,因此式(3)有无穷多个解,是个欠定问题(病态问题)。而CS理论在信号x是K稀疏的前提条件下,若测量矩阵满足一定条件,则原信号可由测量值通过求解一个零范数最优化问题精确重构出来。 超分辨率问题本质上就是一个从低分辨率图像,根据某些先验知识或对成像模型的假设,恢复出高分辨率图像的一个反问题,也是一个从低维空间的信号恢复高维空间信号的问题。这与CS理论的重构具有异曲同工之妙。压缩感知中的测量值y可视为低分辨率图像,是高分辨率图像x的测量值。 超分辨率的高维重建又与CS理论有微小的差异。此时的测量矩阵不再基于设计者的选择确定,而是一个包含对图像模糊化和降采样的降质模型。此外,此时的稀疏基Ψ不需要一定是正交基,也可以是任意的冗余字典,记为D∈RN×K(K≫N)。 将超分辨率问题在CS理论的框架下进行公式化表示。SR问题是从一个或多个低分图像Y中重构恢复出高分图像X。低分辨率图像是从降质模型中获取,即 (4) 将整个图像降质模型表示为一个矩阵算子L=RLp,把矩阵L称作超分辨率问题的投影算子,这就和压缩感知的测量过程式(1)与之对应。那么,超分辨率重建的问题就是降质算子的逆算子,这是一个病态问题,因为式(2)的降质模型造成了信息的丢失。 假设x∈RN是原图像X的一个子块拉伸成的一维向量,存在一个过完备字典D∈RN×K使得x稀疏表示为 x=Dα,‖α‖0=S,S (5) 则低分图像块表示为 y=Lx (6) 式中,y是x的低维投影,相当于压缩感知中的测量值。 将式(5)代入式(6),得到 y=LDα (7) 稀疏向量α可以通过求解优化问题得到。 CS理论的出现为解决欠定问题提供了全新的视角,在没有关于信号支撑的先验知识的情况下,其可以使用比传统方法更少的测量值重构稀疏或可压缩信号。CS理论突破了传统采样理论的限制,即对信号的采集和重建必须遵循Nyquist抽样理论。压缩感知已经应用于各种领域,如机器学习[16,17]、无线通信[18,19]和医学成像[20,21]。 CS理论因其可以降维的优势,可以用于解决超分辨率问题。CS理论和稀疏表示在SR 恢复领域的应用,引起了大量研究人员的兴趣和关注。最早的基于CS理论的超分辨率重构研究可以追溯到文献[22-27],其中,Sen等人提出了可以直接从单个低分辨率图像生成超分辨率图像,而无需使用训练数据集的方法[22],文献[25-27]在此基础上进行了扩展,提出了基于稀疏表示的单图像SR 问题的新方法。 基于迭代收缩和全变分稀疏表示的SR方法将两步迭代收缩算法和全变分(Total Variation,TV)稀疏表示相结合,构建了一种单幅图像的超分辨率重建方法[28]。为了后续叙述方便,将这种方法简称为TVCS_SR。该方法不需要训练集,仅需单幅LR图像实现重建,创新点主要包括两个方面:第一个方面,在测量矩阵里加入下采样低通滤波器,使得SR问题满足应用CS理论的有限等距性质(Restricted Isometry Property,RIP);第二个方面,在重建时通过全变分函数,利用两步迭代法引入TV去噪算子,避免了直接对算子求逆。全变分正则化能保持边界的对比度与锐度[29]。 利用两步迭代算法和全变分正则化实现了超分辨率重构,其核心是在对前一估计值降噪处理的基础上,利用两步迭代收缩得到新的估计值。 基于小波域的压缩感知SR方法[30]在小波域对LR图像进行分解,分别得到其低频与高频子带。在此基础上,利用CS技术分别对低频子带与高频子带进行重建,同时通过小波逆变换获得重建后的HR图像。为后续叙述方便,将这种方法简称为WaveletCS_SR。基于小波域的方法主要包括基于小波变换对图像进行重建和基于CS的高低频子带图像重建两个部分。 3.2.1 基于小波变换对图像进行重建 小波变换是一种时频分析技术,可在时域和频域获得表征信号局部特征的能力,广泛应用与图像分析中。根据不同小波基函数的特点及低分图像特征,文献[30]采用了由Cohen等提出的CDF97小波,其满足线性相位的要求,且运算速度快,同等条件下,比Haar小波快两倍。 假设M×N维的LR图像为I0,基于CDF97的SR重构步骤如下。 步骤1利用小波变换将LR图像分解为4个子带图像,即低频子带LL和LH、HL和HH等3个高频子带,分别对应水平、垂直和对角线方向。 步骤2基于小波变换对LL再次分解,获得下一级的4个子带图。 步骤3对低频子带图进行插值放大,得到重建图像的低频子带。 步骤4分别对3个高频子带进行插值放大处理,得出重建图像的高频子带。 步骤5利用小波逆变换分别对高低频子带进行重构,得到HR图像。 3.2.2 基于CS的高低频子带图像重建 在基于小波域对图像进行超分重建的过程中,高低频子带的获取很关键。由于高频子带图像均具有方向性,若采用传统的插值法,重建后的图像视觉效果较差,图像质量较低。然而,CS技术却可以在较小的失真率前提下实现对原信号的高精度恢复,以保证图像的边缘细节等关键信息,获得理想的重构视觉效果。基于CS的高低频子带图像重建步骤如下。 步骤1初始化余量r0=y,迭代次数n=1。 步骤2计算图像信号能量 c=ΦTrn-1=<ΦT,rn-1> 步骤3利用TV函数对信号进行去噪处理。 步骤4选取c中能量最大的2K个元素,对应的原子构成支撑矩阵ΦI。 基于CS的高低频子带图像重建过程如图4所示。 图4 基于CS的高低频子带图像重建过程 压缩感知中的字典学习已广泛应用于图像超分辨率重建中。基于冗余字典的SR方法基于压缩感知理论,构造了两组冗余字典,分别用于表示LR图像和HR图像的子块。其中,在字典训练阶段使用K奇异值分解(K-SVD)算法进行训练。基于冗余字典的SR方法减小了字典训练所需时间,同时也显著提高了重建HR图像的主客观质量,其重建过程如图5所示。为后续叙述方便,将这种方法简称为Dic_SR。 图5 基于冗余字典的SR方法重建过程 基于冗余字典的图像超分重建的关键点在于,对于一个低分图像的图像子块和其对应的高分图像子块,可分别用低分辨率冗余字典DL和高分辨率字典DH进行表示,而两者的表示系数满足某种规则。冗余字典主要利用K-SVD字典训练方法得到。输入的低分辨率图像可以在更新后的低分辨率字典稀疏基上表示为稀疏系数,然后用对应于高分图像字典的稀疏系数重建高分辨率图像块。 压缩感知理论为解决超分辨率问题提供了理论基础,如上所述,利用高分辨率及低分辨率冗余字典对重建出高质量的高分图像已取得了很好的效果。然而,图像自身以及不同尺度的图像之间,都存在着一定的结构相似性,将这种图像内部的自相似性以及不同尺度的非局部相似性应用在基于冗余字典的超分重构中,也显著提升了重构后图像的质量。 基于分类字典与非局部相似性的SR方法[32]是基于压缩感知和自相似约束的图像SR算法。为后续叙述方便,将该方法简称为ClassDic_SR。 在字典训练部分中,利用基于测量域的分类字典训练方法可以使用最合适的字典重构感兴趣的LR图像。如果仅仅从外部图像数据库中学习先验知识,则往往会产生重建的HR图像的不真实细节。通过充分利用图像的相似性及图像的非局部相似性,搜索整个图像中的相似块,将图像块的稀疏性和自相似性作为优化问题的约束进行求解。具体来说,首先,提出了一种基于测量域的字典分类方法,通过分析测量域中的特征,图像块被分类为平滑、纹理和边缘部分。然后,使用分类的图像块训练相应的字典。此外,在重构部分,使用联合CS重构方法恢复HR 图像,同时,考虑图像的非局部相似性和稀疏性作为约束。 3.4.1 字典分类方法 纹理分类是图像处理领域的重要研究方向之一。考虑到算法复杂度,探寻一种能够降低处理数据维度,同时又不会导致图像信息丢失的纹理分类方法至关重要。压缩感知理论很好地解决了这个问题,其可从少量采样值中高概率恢复出原始高维信号[33-35],同时,测量域的数据量又远小于像素域的数据量。测量域分析信号快速高效,可以高精度地对图像块进行纹理分类,同时还能够保证在对图像进行重构时不损失图像的信息。字典分类方法的重建过程如图6所示。 图6 字典分类方法的重建过程 在压缩感知图像处理领域,可以直接分析图像块的测量域信息得出图像的结构和细节信息[36]。将图像在测量域的相关性作为依据对图像块进行划分,在此基础上,利用K-SVD算法针对每一类图像块分别训练对应的冗余字典。 3.4.2 图像非局部相似性的CS超分方法 一幅图像内部,自身存在着一定程度的相似性和可重复性,这包括像素上的重复性以及子图像块的相似性。图像里的某个像素,均可以表示为两个邻像素的加权之和。加权系数的值取决于两个像素与当前像素的相似性。一般来讲,相邻像素的相似度更高,但实际上,距离较远的两个像素也具有相似性或者一致性。受此启发,将图像内部的相似性和可重复性用于超分重建算法。 一幅图像自身内部的图像块之间,比外部训练数据库中图像块更为相似[37]。将图像的非局部自相似信息与外部字典相结合,提出了图像非局部相似性的CS超分方法。图像在不同尺度之间也有许多相似的块,较大的搜索区域会产生更多类似的块,可采用变步长搜索方法寻找相似块。在目标图像块的相邻区域,采用螺旋式块搜索,而对于非邻区域,则增加步长进行搜索。这种方法可以充分挖掘图像中的类似信息。 对于输入LR图像的任何图像块y,根据其方差选择相应类别的字典对DL和DH。在整个图像中找到所有类似的块S={y1,y2,…,yn}。将自相似性作为优化问题的约束,需要α的非零值元素数量很少,由α表示的高分图像块与其类似的块S具有高度相似性。使用S、DL和DH的联合重构方法的计算表达式可表示为 (8) 式中:F为特征提取算子;参数λ用来平衡解的稀疏性和对图像块的近似程度。式中的前两项用于保证输入LR图像块的保真度,中间的l1正则化项保证LR块在DL上的稀疏性,最后一项确保恢复的HR图像块和类似块之间的近似程度。近似程度由γi控制,可表示为 其中:Z为归一化参数;h为控制衰减速度的参数。 求解式(8)得到系数α,利用 x=DHα (9) 获得HR图像块。处理得到的所有LR块,即可恢复HR图像X。 图像非局部相似性的CS超分方法的重构过程如图7所示。 图7 图像非局部相似性的CS超分方法的重构过程 SR方法的性能从主观和客观两个角度进行评价。主观评价主要是基于人眼的视觉感知评估图像的质量,每个个体对图像的关注点各不相同,主观评价存在个体差异。客观评价是使用计算方法,对比原始的高分图像与重构得到的高分图像的相似性,常用的两个标准是峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)和结构相似性(Structural Similarity Index,SSIM)。 选取数据集Set5、Set14、BSD100和Urban100中部分图像,分别利用Bicubic、TVCS_SR、WaveletCS_SR、Dic_SR和ClassDic_SR等5种典型超分算法进行超分辨率重建,并利用PSNR和SSIM对重建HR图像的质量进行评价。图8为放大因子为2时重建后HR图像的主观效果,图9为放大因子为4时重建后HR图像的主观效果。表1和表2分别为5种方法在4种数据集进行实验得出的PSNR值和SSIM值。 图8 放大因子为2时重建HR图像的主观效果 图9 放大因子为4时重建HR图像的主观效果 表1 5种方法在各个测试数据集上的PSNR值/dB 表2 5种算法在各个测试数据集上的SSIM值 由图8和图9中的主观视觉结果可以得出,使用基于CS理论中的冗余字典方法重建图像具有丰富的纹理区域、更自然的轮廓,且没有明显的振铃效应和锯齿形效果。这是由于引入了图像的自相似性作为图像重构的约束,这种自相似性提供了图像内部相邻像素和非相邻像素的相关性特征,进行SR重构时,得到的高分辨率图像的结构更接近原始的高分图像,故从主观视觉上看优于其他算法。由表1和表2可知,基于压缩感知冗余字典的方法比其他算法具有更好的客观质量,PSNR和SSIM均得到改善,PSNR 值比Bicubic增加了约5.4~6.5 dB,比其他3种CS方法增加约1.1~5.2 dB;SSIM值较Bicubic增加约0.11~0.15,比其他3种CS方法增加约0.01~0.13。因此,CS理论中的冗余字典方法性能较插值法更优,而考虑了图像相似性并结合CS感知理论的SR方法则优于未考虑图像相似性的方法。 介绍了超分辨率及压缩感知的相关概念,并探讨了压缩感知与超分辨率问题的内在联系。通过分析对比几种典型的基于压缩感知的超分重构方法的性能,得出利用压缩感知技术的超分方法展现出了较传统算法的优越性,同时将图像的自相似性作为重构高分辨率图像的约束条件,也进一步提升了重建后高分图像的质量。 对图像进行超分辨率重建时,采用字典训练提取高分辨率图像和低分图像之间的映射关系,这种映射关系的学习还不够精确,需要一种更加高效的算法来构建二者的映射关系,后续研究可将稀疏表示与深度学习相结合,应用卷积神经网络框架对图像的稀疏特征进行学习,从而构造稀疏字典,再利用稀疏字典对图像进行超分重构。此外,超分辨率算法对图像降质模型的模拟依赖性很强,已有的降质模型的估计方法无法很好地应对复杂和恶劣的成像环境下的模型估计,当实际情况与模拟的降质模型差别较大时,重构图像的质量受到很大影响,因此,还需要继续深入研究对降质模型的更精准估计模拟方法。
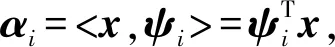

2.2 超分辨率与压缩感知理论的内在联系
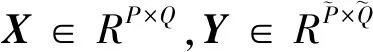
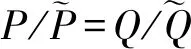
3 典型的基于CS的超分辨率方法
3.1 基于迭代收缩和全变分稀疏表示的SR方法
3.2 基于小波域的压缩感知SR方法
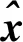
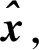

3.3 基于冗余字典的SR方法

3.4 基于分类字典与非局部相似性的SR方法
4 几种典型方法性能对比
4.1 超分辨率评价指标
4.2 性能对比


5 结语与展望
