多目标跟踪数据关联算法综述

蔡秀梅，王 妍，卞静伟，吴成茂

(1.西安邮电大学 自动化学院, 陕西 西安 710121； 2.西安邮电大学 电子工程学院，陕西 西安 710121)

计算机视觉是以传感器和计算机为核心模拟人类视觉的数字系统，在实际应用中，计算机视觉系统基本上都是通过不同种类的摄像机获取和处理数据。计算机视觉是人工智能的眼睛，是未来自动化获取数据的主要渠道之一，也是处理数据的重要工具之一。随着信息技术的发展，仅靠人类的视觉系统已经无法处理日益增长的视频数据，因此，计算机视觉技术的发展变得尤为重要。

视频目标跟踪是对传感器获得的一系列连续视频帧进行分析得到目标在每一视频帧中的尺度、行为、状态、运动速度和位置等检测参数信息，持续跟踪目标并进行轨迹预测，找到特定目标的轨迹信息。因此，视频目标跟踪是视觉领域的一个发展基础和重要的关键难点。

依据视频图像中所有需要进行跟踪的目标个体数量的不同，将其分为针对单个目标[1]和针对多个目标的跟踪[2]。单目标跟踪仅可以得到视频中一个物体的运动轨迹。这个目标是由初始帧标定，没有其他与目标有关联的先验信息，根据跟踪算法得到未来视频序列中目标的标记框位置，形成目标轨迹。多目标跟踪是对视频环境中存在的全部目标状态完成估计操作，使得处于不同帧中各个目标可以形成各自的轨迹。

目前，目标跟踪在军事、民用等领域中普遍使用。

视频目标跟踪在军事上的使用主要包括以下4个方面：1)当进行军事防御时，跟踪系统能够对出现的陌生目标信息发出报警信息，并在作战中对特定的目标进行瞄准射击；2)当前智能导弹的技术采用目标跟踪技术可以准确地对目标进行跟踪并完成精准攻击；3)一些自动火炮等常规武器可以通过视频的监控系统对对方目标准确跟踪，从而提高作战效率；4)通过视频目标跟踪监控系统也可以在国境线上建立可靠的无人侦察系统。

智能视频监控是指人眼用镜头替代，大脑用计算机替代，对视频中存在的目标进行监控、跟踪，当发生危险信号时能够迅速发出报警信息。现在虽然在大型商城、考试、博物馆、交通和银行等重要场所都安装视频监控，但并未有智能性，还是需要大量的人工操作，而人工操作中由于其注意力、速度等问题，导致通过视频系统处理问题具有滞后性，因此，为了预防犯罪、解脱人力及减少对人为操作的依赖，自动对视频中目标进行监控、分析和报警，使博物馆发生物品丢失时迅速发出报警信息。当进行车牌识别时，能迅速捕捉到牌号，并判断是否牵涉刑事案件等。

无人驾驶是在计算机系统下进行无人自动安全驾驶。通过一系列传感器、摄像头等设备获取车辆行驶的速度和方向等信息，并对车辆前后左右的行人和车辆信息进行获取，通过跟踪算法对周围行人、车辆的速度和状态进行预估，使车辆与行人之间保持安全车距和安全速度。相对于手动驾驶，使用这种技术能够迅速判断出车辆行驶的信息，并能保持安全驾驶，保障了交通安全。

随着目标跟踪应用的范围越来越广，引起了大量科学研究者的普遍关注。经历了逐年的不断探索，跟踪技术获得了显著的成果[3-4]。虽然有多种目标跟踪算法，但是多目标跟踪中的主要步骤大致可以分为目标检测、运动预测和数据关联。数据关联是多目标跟踪的一个重要阶段，因此，为了全面系统地了解多目标跟踪现状，通过介绍数据关联的经典方法，对多目标跟踪中的数据关联技术进行分析，总结各个数据关联算法的研究进展及存在问题，进而展望数据关联未来的发展趋势。

1 数据关联技术

在单目标跟踪中，由于区域中只有一个目标需要被跟踪，因此，每次经过检测得到的样本中，只有一个样本是来自于这个目标的，其他的数据都可以看做是干扰所导致。和单目标跟踪比较，多目标跟踪要对多个观测和多个目标进行关联。多目标跟踪中的关联操作通常分为两类，一类是解决观测样本中存在的不确定性因素，完成观测样本和轨迹集之间的关联，一类是解决目标的状态估计。关联操作处理的重点是观测样本和已经确定的目标轨迹之间的关联，当观测到目标后，需要判断这个观测来源于真实目标还是环境干扰，如果来源于真实目标，还需要判断是从哪个目标得到的观测。数据关联是目标跟踪过程中极为关键的问题，其直接影响到能否正确分离目标和跟踪目标。

在进行观测时，传感器系统总是存在着观测误差的影响，不能判定所得的观测数据是由真实目标还是虚假目标产生，或者由于目标被遮挡、目标状态发生突变导致目标信息丢失没有被观测到等问题，使得数据关联变得尤为复杂，因此，需要对数据关联中的一些经典方法进行详细的介绍。

2 数据关联经典方法

经典的数据关联方法主要包括以下4个方面：1)1973年Singer提出的基于决策的最近邻法(Near Neighbor Data Association，NNDA)[5-6]；2)基于概率统计的多假设跟踪(Multiple Hypothesis Tracking,MHT)[7]、1972年Tse等研究者提出的基于贝叶斯公式的、适合处理杂波环境下的稀疏目标跟踪时的概率数据关联算法(Probability Data Association，PDA)[8-9]、以PDA算法为基础提出的一种适合处理多目标跟踪的联合概率数据关联算法(Joint Probability Data Association,JPDA)[10]；3)基于粒子滤波的数据关联[11-12]；4)基于模糊逻辑的模糊数据关联算法[13]、以模糊聚类算法为基础的关联算法[14]等。

2.1 最近邻法

有很多完成数据关联操作的算法都能得到比较好的效果，其中NNDA算法是最早的一种方法，也是在一定情况下最有效的算法。最近邻算法利用欧氏距离比较每个观测样本与目标之间的距离，然后将距离最近的观测样本当作目标的真实状态，该算法不依赖于耗时的蒙特卡罗模拟，是一种基本的分类回归方法。

2.1.1 算法原理及优缺点

NNDA算法的输入是基于实例的学习，没有训练阶段，将新样本直接与训练集做分类或回归预测。此算法使用的模型实际上对应于特征空间的划分。

NNDA是一种简单的数据关联算法，能有效地解决单目标跟踪问题，其核心思想是利用距离函数判断量测与目标的关联对，先通过设置跟踪门，筛选得到候选回波，其中跟踪门是指以上一次的目标预测位置为中心得到的区域，如果落入跟踪门只有一个量测，则此量测和目标形成关联对，如果跟踪门内有多个候选回波，此时需要判断各候选回波与中心的距离，选择距离最小的回波作为目标回波。

此算法只需要通过距离就可以对目标进行分类，计算简单，但是当数据量比较大时，通过此算法计算距离目标预测位置最近的回波可能不是被跟踪目标的真实回波，容易出现跟丢目标的情况，并且，在进行分类时没有考虑目标的速度及其他的状态信息，导致对漏检、误检和虚检的观测结果比较敏感，只能适应于稀疏目标杂波较小的情况。

2.1.2 改进方案

NNDA中的距离度量通常采用欧氏距离进行判定，但欧氏距离只考虑了两个样本之间位置的相近程度，没有考虑两个样本之间的相关性和不确定性，因此，可以通过采用马氏距离弥补此不足[15]。其通常只适用于单目标跟踪，当目标数较多时可能会出现误跟目标的情况，可以通过改进运动模型更新目标状态[16]或者增加目标的信息维数[17]，能有效降低该方法中误关联对跟踪效果的影响。除此之外，基于最近邻法进行数据关联时会出现系统误差补偿，采用最近邻-点拓扑图的关联算法[18]可以有效地克服最近邻方法对系统偏差敏感的不足。

2.2 多假设关联

多目标跟踪是一个无监督模式识别问题，0～1整数规划是多假设关联的一个雏形，通过执行各种组合的多假设测试以确定许多可行轨迹的特定组合最有可能代表的实际目标。20世纪70年代，Reid以0～1整数规划方法作为基础，并将全邻最优滤波器和Bar-Shalom的聚概念进行结合，提出了一种新的数据关联技术，叫做多假设跟踪法[19]。多假设关联是一种基于多帧的数据关联技术，其不仅与当前量测有关，也与历史量测有关，在理想条件下，该算法是最优的数据关联算法，具体执行过程如图1所示。

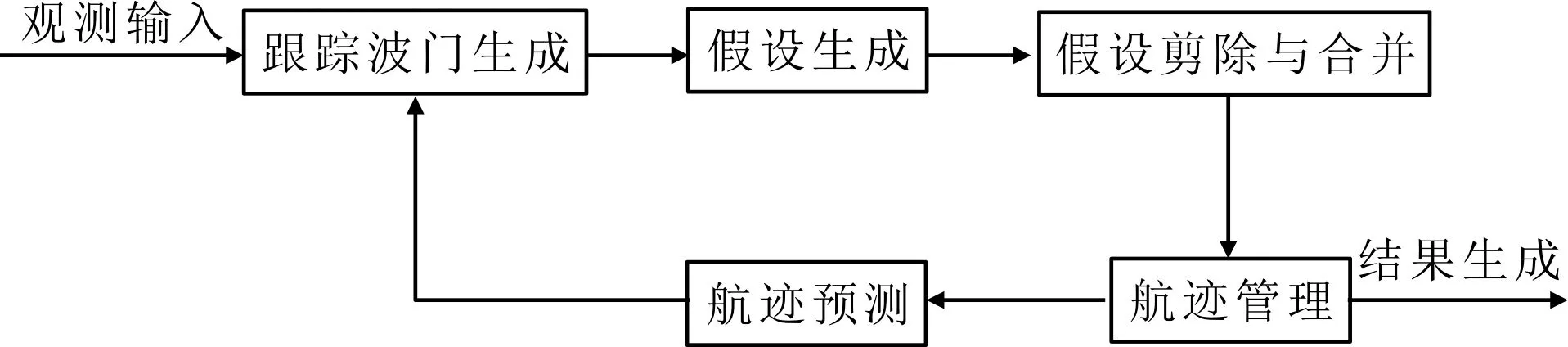
图1 多假设跟踪算法执行过程

2.2.1 算法原理及优缺点

MHT算法考虑回波来源于目标、杂波和新目标等各种可能的情况，通过对量测序列的各种划分进行整体寻优寻找可行轨迹，MHT是一种根据多个扫描周期的量测进行数据互联的技术。多假设关联包括数据聚簇、假设生成、假设删除和假设矩阵管理等4个处理过程。数据聚簇分别将新接收的量测和历史假设进行关联，形成新的假设。假设生成对于每个簇关联的量测形成新的假设，同时更新目标的状态。假设删除主要是消除不可行假设。假设矩阵管理将假设航迹转换为确认航迹，并且删除不可能存在的假设航迹。其中，假设生成和假设删除是其中最核心的步骤。

1)假设生成。在MHT算法中，通过产生一组关联假设用于描述每个观测值的一切可能由来。

假设由状态变量构成的向量x(k)表示每个目标，则状态方程表达式为

x(k+1)=Φx(k)+Γw(k)

其中：Φ表示状态转移矩阵；Γ表示噪声矩阵；w表示协方差为Q的白噪声向量。状态变量与观测值相关联，k时刻的观测值表达式为

Z(k)=Hx(k)+v(k)

其中：H代表着一种观测值矩阵；v代表以R作为协方差的噪声向量。

Zk={Z(1),Z(2),…,Z(k)}

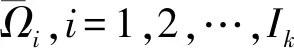
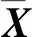
2)概率计算。k时刻第i中假设的概率计算表达式为

式中：g为归一化常数；P′表示检测概率；N表示前一帧中的目标数量；N′表示观测得到的目标数量；β表示杂波的密度；T表示杂波数目；β′表示新目标在检测空间中的密度；T′表示新目标数目。

如果第m个量测值来自杂波或者新目标，则有

式中，V表示监测区域所占的面积或者体积。

倘若第m个观测值源于确定或不确定的目标，则有

其中，N(·)是正态分布。

该算法能够检测出目标数随时间推移而变化的情况，并且全面地考虑了跟踪过程的假设来自于目标、虚警还是新目标的可能，其兼容性和一致性较高，综合了NNDA和JPDA的优点。但是此种算法依赖于目标和杂波的先验知识，并且需要考虑各种假设，导致关联时效率不高。

2.2.2 改进方案

目标跟踪过程中要考虑多种假设的情况，使得数据关联的效率较低，文献[20]提出了一种基于利用似然比航迹得分简化后的线性分配LAP的多假设跟踪方法，该算法利用航迹的对数似然比作为假设航迹得分，替换传统多假设跟踪中使用的匹配效率。此外，目标跟踪中受杂波等的影响，导致跟踪过程中容易出现虚警等情况，可以通过引入灰度信息等多种特征重新构造航迹置信度函数和航迹启动条件，从而增强算法抑制虚警的能力[21]。文献[22]提出一种基于多假设的目标检测跟踪算法，该算法利用检测前跟踪原理和目标运动和航向稳定性特征，优化多假设核心算法。

2.3 概率数据关联

针对测量数据来源不确定时的跟踪问题，1972年Bar-Shalom和Tse[8]认为不该将预测误差中最小的观测位置当作目标在下一帧中的位置所在，而应当对于跟踪门内的一切观测样本实行加权平均并当作滤波输出，从而获得更加多的后验消息，提出适合杂波环境下单目标跟踪的概率数据关联算法，此算法是一种基于贝叶斯公式的数据关联算法。

2.3.1 算法原理及优缺点

PDA是当跟踪波门内采集到多个量测时，不同于NNDA只选择其中的一个量测，而是考虑波门内所有的量测，并根据相关情况计算量测来自于目标的概率。依据概率值对量测进行加权，并利用加权值对目标的状态信息进行更新。PDA主要对处于杂波环境中稀疏的、单目标的跟踪问题进行处理。

假定直到k时刻处于跟踪门内的有效量测累积集合的表达式为

Zk={Z(1),Z(2),…,Z(k)}

其中，Z(k)表示在k时刻落入目标跟踪门内的所有量测，那么在量测累积集合条件下，定义k时刻第i个有效量测来自目标的后验概率为

Li(k)=L[θi(k)|Zk]

其中：θi(k)表示第i个量测源自目标这一事件的概率；θ0(k)表示k时刻没有观测来源于目标的概率。由此可知，目标在k时刻均方意义下的最优估计为

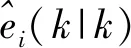
PDA在单目标跟踪时跟踪目标性能良好，并且只对波门内点迹的关联概率进行计算，计算量不大，实时性较好，其存储量与标准卡尔曼滤波几乎相等，易于实现。但是只适应于路径平滑的目标，否则会丢失目标，并且当目标数比较密集时，跟踪的性能比较差，可能会造成错误分类，容易出现误跟的现象。除此之外，PDA要求信息来源确定，否则此时概率数据关联是一个不理想的贝叶斯估计。

2.3.2 改进方案

针对PDA只能处理单目标跟踪问题，文献[23]提出了一种在杂波环境下，利用多普勒信息进行辅助的跟踪算法。此算法利用多维信息进行有效量测的筛选，从而将一个多目标数据关联的问题转化为多个单目标数据关联的问题。为了提高目标跟踪中的实时性和精确性，文献[24-25]引入距离加权的概念，区分来自于目标的量测概率和来自于杂波的虚假概率。文献[24]提出了通过对距离进行加权的概率数据关联跟踪算法，经过对关联概率的距离加权将量测分布的先验信息明确地表达出来。文献[25]也提出了一种针对距离加权的PDA通过基于距离二次加权的关联概率对目标状态进行更新，从而提高目标跟踪的性能。针对目标运动过程中存在的不确定性问题，考虑引入交互多模型，文献[26]提出了一种概率数据关联交互多模滤波算法，该算法基于全协方差扩展式卡尔曼滤波框架，采用交互多模滤波方法解决了机动目标运动过程中的模式不确定性。文献[27]提出了利用自适应关联门的一种跟踪方法，此方法是将传统的交互多模型概率关联算法作为基本，采用假设前提下得到的目标预测观测和当前真实预测观测，修正信息协方差，使其尽可能地包含目标真实量测点迹。为了充分利用目标的特征信息，文献[28]提出了一种基于人类视觉选择性注意机制和知觉客体的“特征整合”的认知雷达关联方法。此方法是将综合交互多模型概率数据关联算法作为基本，采用“当前”统计模型和允许运动模型作为模型集，实时交互使关联波门能随目标机动调整。文献[29]提出了一种特征辅助的概率数据关联算法，该算法同时利用了目标的特征信息和状态信息进行数据关联，提高了关联时的准确性。

2.4 联合概率数据关联

JPDA是多假设方法的一个特例，是Bar-Shalom和他的学生在PDA的基础上提出的。PDA是基于计算发现的每个候选测量的后验概率。假设只有一个目标存在，并且其他所有测量都是泊松分布，JPDA计算泊松分布中多个目标的联合后验概率。JPDA与PDA相似，但是其关联概率是由所有目标的所有量测值计算得到的，因此，JPDA综合考虑了多个可能并进行了结合。

JPDA针对多个目标的跟踪门相交情况进行了详尽的分析，能较好地适应密集环境下的多目标跟踪，其包括联合事件生成和关联概率两个部分。

2.4.1 算法原理及优缺点

JPDA算法基本思想是对应于落入跟踪门相交区域的情况，这些观测数据可能来源于多个目标，JPDA的目的在于计算观测数据与每一个目标之间的观测概率，并且认为一切的有效回波都有可能来源于每一个目标，只不过来源于不同目标有着不同的概率，JPDA的算法原理如图2所示。

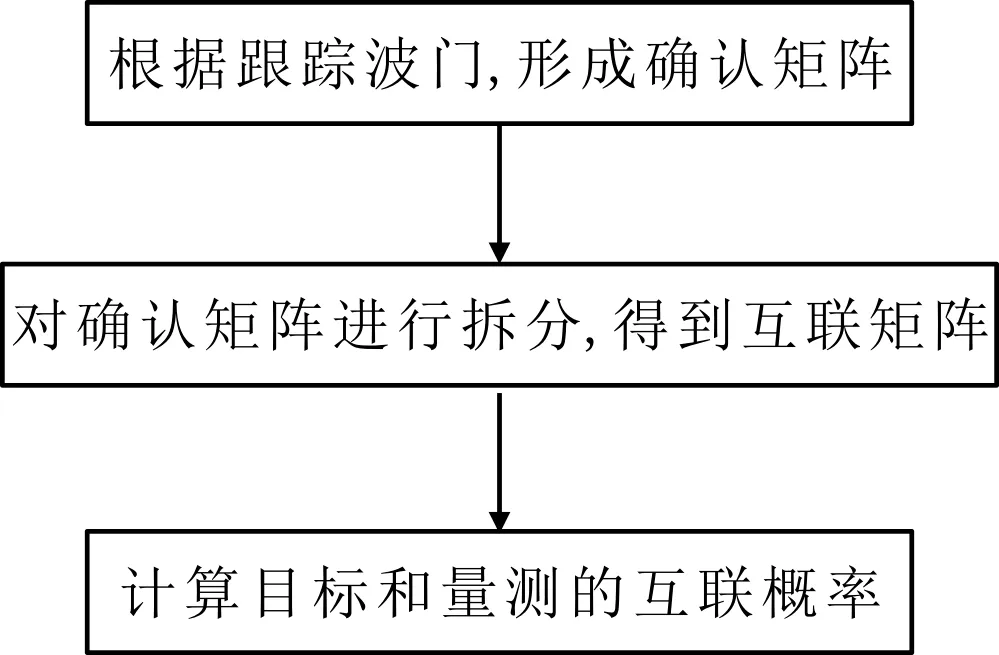
图2 JPDA原理

假设在杂波环境下已有T个目标，t表示目标的编号，nk表示有效量测总数量，j表示有效量测值的编号，则其状态方程和观测方程分别为

xt(k+1)=Φt(k)xt(k)+w(k)

Z(k)=H(k)xt(k)+v(k)

其中：xt(k)表示k时刻目标t的状态向量；Φt(k) 表示目标t的转移矩阵；w(k)和v(k)表示以零为平均值的白噪声；H(k)表示观测矩阵。

为了表示有效回波和各个目标跟踪门的复杂关系，引入了确认矩阵的概念。当且仅当回波处于某个目标关联区域之内，才被当作是有效的回波，否则就会被否决。由此，就能获得包含nk个有效回波，T个目标的确认矩阵，表达式为

ξ=[ζjt]j=1,…,nkt=1,…,T

其中，ζjt=1表示观测j处于目标t的跟踪门里，而ζjt=0表示观测j没有处于目标t的跟踪门里，任意量测都有可能源于杂波或者虚警。因此，t=0表示没有目标，ζj0全为1。

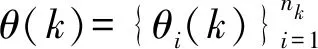
Ljt=L{θjt|Zk}

根据全概率公式，有

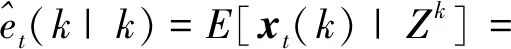
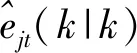
JPDA算法不需要任何关于目标和杂波的先验信息，能够充分利用跟踪门内的所有回波获取可能的信息。但是难以确切地得到联合事件与关联事件的概率，并且当目标和量测数目较多时，该算法的计算量测与目标数的阶乘近似成正比，会出现组合爆炸的现象，导致计算复杂。

2.4.2 改进方案

考虑多传感器采集到的信息存在较大差异，以及传感器自身的原因，传感器不能稳定地跟踪某个目标，要想进行关联融合需要进行一定的坐标转换。针对此问题，文献[30]提出了基于JPDA的车用多传感器目标跟踪融合算法。先建立了基于改进的JPDA的单传感器多目标跟踪算法，再用相关序贯关联法进行多传感器间目标的关联，最后，利用凸组合融合算法将关联的不同传感器目标进行融合。此外，多目标跟踪要求系统快速跟踪到目标，但是系统存在非线性问题，使用传统方法导致跟踪误差偏大。为解决上述问题，文献[31]提出将高斯-厄米特粒子滤波算法和JPDA相结合，利用高斯-厄米特滤波计算的均值、协方差产生密度函数并生成具有后验特征的粒子，用JPDA进行杂波提出和数据关联。针对量测数多导致计算复杂的情况，文献[32]提出了一种基于JPDA的复杂情况下视频多目标快速跟踪方法。该算法首先采用murty算法求JPDA的最优a个联合事件，再根据JPDA的关联概率讨论目标的运动情况，分析在多目标新出现、遮挡、消失和分离等复杂情况下，当前帧量测与跟踪目标的数据关联问题，获取复杂运动的多目标跟踪航迹。文献[33]提出了一种基于元数据的数据互联算法。该算法减少部分关联的计算量，同时为点迹和航迹的特征建立相关的元数据，有效地减少了算法的计算量和数据互联的错误率。文献[34]提出了一种基于聚类算法的联合概率数据关联算法。该算法在JPDA基础上，运用模式识别中的聚类思想对传感器所接收到的量测数据进行聚类，减少量测数目，从而简化了有效矩阵，减少了原有算法的计算量。

2.5 粒子滤波

在贝叶斯后验概率的计算过程中需要用到积分，但是对于一般的非线性、非高斯系统，很难得到后验概率的解析解，由此引进粒子滤波(Particle filtering,PF)。PF是一种近似的贝叶斯滤波算法。其通过使用粒子集代表概率，能够用于各种形式的空间模型上。PF技术能够在非线性、非高斯系统得到较好的效果，这一特性使其使用范围非常的宽泛。跟踪领域中，Hue[35]将PF扩展于多目标跟踪领域以及数据关联中。

2.5.1 算法原理及优缺点

PF是一种基于单假设的数据关联方法，其本质思想是将从后验概率中抽取出来的随机状态粒子代表其分布状态。PF可以被应用于非线性、非高斯系统系统，其粒子波原理如图3所示。

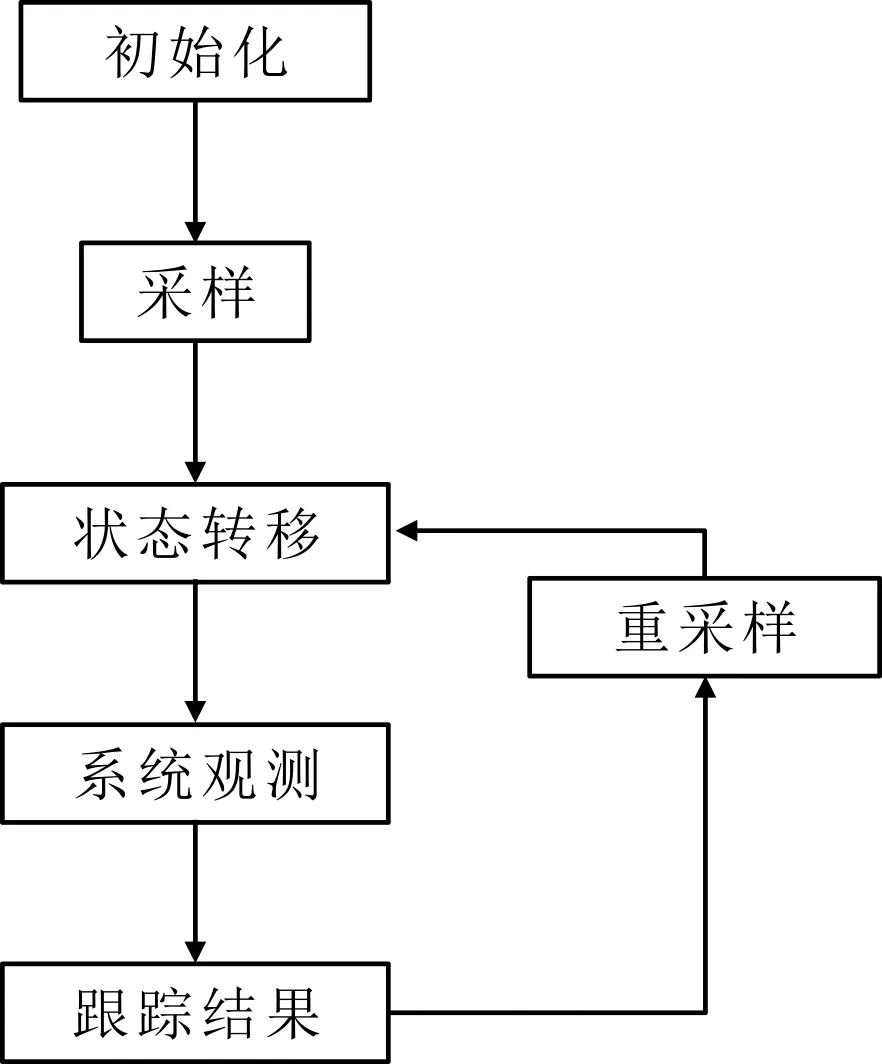
图3 粒子滤波原理

在标准粒子滤波器下，假设时刻k目标的状态为x(k)，考虑通过观测状态Z(k)找到目标状态，其中观测器从第一帧到第k帧为Z(1:k)，在粒子滤波器中，后验概率分布可以通过查普曼-科莫高洛夫方程的近似模型定义，粒子集表示为{x1(k),x2(k),…,xb(k)}，b表示粒子数量，权重集表示为{ω1(k),ω2(k),…,ωb(k)}，则有

其中，q表示重要性密度函数。

前一次的后验概率分布为

其中，δ(·)是一个狄拉克函数。

粒子滤波的基本过程包括初始化、权重计算、重采样和状态估计等4个方面。

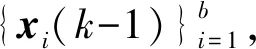
2)权重计算。计算每个粒子xi(k)的重要性权值，其公式为

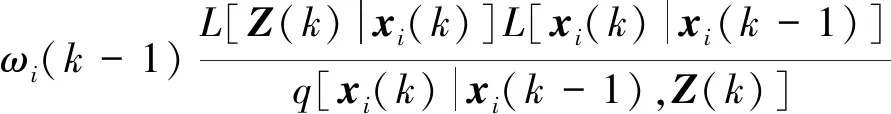
归一化重要性权值后，表达式为

3)重采样。根据粒子权重对粒子进行筛选，有效粒子数的计算公式为

4)状态估计。根据所有粒子权值和状态计算得到目标状态估计，其表达式为

方差估计的表达式为

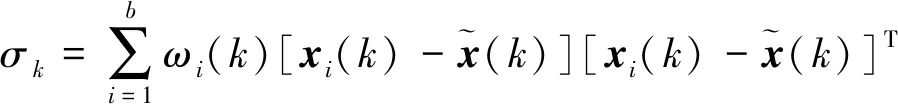
2.5.2 改进方案

当杂波较多时，可以通过融入特征信息降低杂波干扰的影响，文献[36]提出了一种利用高斯混合模型和RBMCDAGMM的实时监控跟踪算法。该算法根据场景中像素点的特征信息，利用混合高斯模型进行建模，并对前景目标进行检测，使用蒙特卡洛数据关联算法降低可能的目标交叉及杂波干扰带来的影响。文献[37]提出了一种实现递归贝叶斯滤波器的算法，此算法不受高斯噪声假设的限制，可以应用于任何状态转移或观测模型，提高了基本算法的效率。传统的粒子滤波算法采用粒子的建议分布函数，没有考虑当前的观测值，大量的粒子运算浪费在那些具有小似然性的区域，文献[38]提出了一种基于均值偏移(Mean Shift)以改进建议分布函数的粒子滤波跟踪方法，此算法有效地利用了当前观测值，有较好的实时性。粒子滤波算法具有滤波精度较低和粒子退化的问题，针对此问题，文献[39]提出了根据扩展卡尔曼粒子滤波的跟踪算法，此算法使用扩展卡尔曼滤波去构建粒子滤波的建议分布函数，使得此函数可以加入新近得到的观测讯息，从而获得每一个契合真实状态的后验概率分布。

2.6 模糊目标跟踪

在目标跟踪过程中，通常目标状态信息中包含着各种各样的参数，通过这些参数构建的模型存在着很多的不确定性，而且数目未知，观测中也存在着很多的未知性，导致使用这些模型进行状态估计和数据关联时会产生更多的不确定性。对于不确定性问题的研究，概率和统计学方法起了不可估量的作用，这也使得概率和统计学成为处理不确定性问题的基本方法，但是统计处理方法也有其局限性。因此，能够处理不确定性问题的模糊数学应运而生。1965年，Zadeh提出了模糊集的概念[40]。近年来，模糊数学正在被广泛地应用于目标跟踪领域。

2.6.1 算法原理及优缺点

对于多目标跟踪中的数据关联实际上是一个分类的问题，基于模糊聚类的数据关联具有简单性和有效性。模糊C均值聚类算法的目标函数为

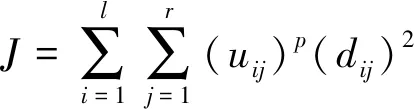
其中：l表示样本数目；r表示聚类中心数；p为加权指数，一般取值为2；uij表示量测属于目标的隶属度；dij表示量测和目标预测位置的欧氏距离，dij=‖ζi-cj‖2；ζi表示第i个样本，cj表示第j个聚类中心。利用拉格朗日乘数法，可推导出模糊隶属度和聚类中心为

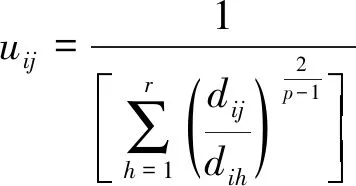
以目标预测位置为聚类中心，计算出隶属度矩阵U。根据计算出的隶属度矩阵，可按以下步骤进行量测和目标的数据关联。

步骤1在隶属度矩阵中查找出uih的最大值，并将量测h与目标i关联。

步骤2在U中删除第i行和第h列，或将第i行和第h列的所有元素赋值为0。

步骤3重复以上两个步骤，直到所有的量测和目标进行关联。

该算法通过将聚类转化为一个带有约束的非线性规划问题，计算简单且速度快，能满足实时性要求，但是其要求某一特定量测隶属于所有目标类的隶属度值的和必须等于1。这就使得量测隶属于某一类的隶属度值不仅与其之间的距离有关，而且与其他类有关，即使量测距离所有类都很远，其隶属度值可能也会很大，且在杂波密度较大时多目标跟踪的准确性会下降。

2.6.2 改进方案

模糊聚类算法对噪声比较敏感，聚类质量较差，文献[41]提出了一种基于数据加权策略的模糊聚类改进算法，通过引入指数因子和影响指数，使其可以在聚类过程中差异化处理各个数据，提高聚类质量。当杂波密度比较大，多目标跟踪会出现精度低、实时性不强等难题，文献[42]提出了一种处于密集杂波环境中的模糊数据关联跟踪算法，该算法以模糊聚类算法作为基础，获得了各个观测样本相对各个目标的模糊概率，并引进一种公共观测影响因子对概率矩阵进行重新构建，将重新构建的关联概率看成权值，最后用卡尔曼滤波实现目标状态的更新操作。

3 结语

目标跟踪在民用和军事中都有着广泛的应用，而数据关联又是目标跟踪的核心问题，因此，数据关联仍然有很大的发展空间。所提的数据关联方法大都是在视频质量良好的前提下进行，当视频出现外界环境干扰较大时，数据关联就表示出不稳定性。一般在局部数据关联时计算复杂，鲁棒性差，全局数据关联时需要严重依靠目标检测的性能。

随着深度学习的发展，已有研究提出将神经网络应用于目标跟踪中的数据关联。神经网络的长处就在于其自学能力和知识获取能力。文献[43]提出了一种基于卷积神经网络的简单在线多目标跟踪。将深度学习应用于目标跟踪可以提高算法的精度，但是计算量会增大，速度会减慢，因此，如何在能提高精度的同时可以不增加计算量是未来研究的难点之一。

当目标在被遮挡时，维持目标跟踪，并且当目标再次出现时立即跟上目标是目标跟踪的一个难点问题。因此，在后期研究过程中如何提高目标在遮挡情况下的目标跟踪问题也是后续研究之一。

以上介绍的算法是后续深入的算法研究的基础，处理相应的问题需要选择相应的算法，有时候需要将算法相互结合以便更好地处理数据关联问题。随着对算法深入的研究，以后还会提出更有效性、更具鲁棒性的算法。