声的产生、反射、折射和极化

法 林，孙 科，房向荣，孔链链，赵 琳，徐澍宇

(1.西安邮电大学 电子工程学院，陕西 西安 710121； 2.西安邮电大学 通信与信息工程学院，陕西 西安710121)

地壳中的页岩等沉积岩通常被认为是具有垂直对称轴的垂直横向各向同性(Vertical Transverse Isotropy,VTI)介质，可以使用六角晶系的弹性刚度矩阵来描述VTI介质的力学特性。这些由许多细薄层构成的沉积岩通常在各自的薄层内表现出微观各向同性特性，而在整体上表现出较强的宏观各向异性特性[1-2]。由于岩石中存在各向异性特征，导致传统的声波测井和振幅随炮检距变化(Amplitude Variation with Offset,AVO)反演分析在应用中存在一定程度的偏差[3-4]。另外，在传统的声波测井过程中，会忽略换能器中声-电或电-声转换产生的能量损耗[5-6]，这也会使测量数据出现一定的偏差。为了提高声波测井与AVO分析的数据精度，需要研究声波在沉积岩中的传播、在不同岩层界面上的反射/折射以及极化[7]等方面的特性。

1 固体-固体界面的异常入射角

声波和光波在反射/折射方面有很多可以相互借鉴的地方，由于光波在反射/折射过程中会出现异常折射的现象，所以声波也可能存在异常折射现象。

1.1 VTI-VTI的界面模型

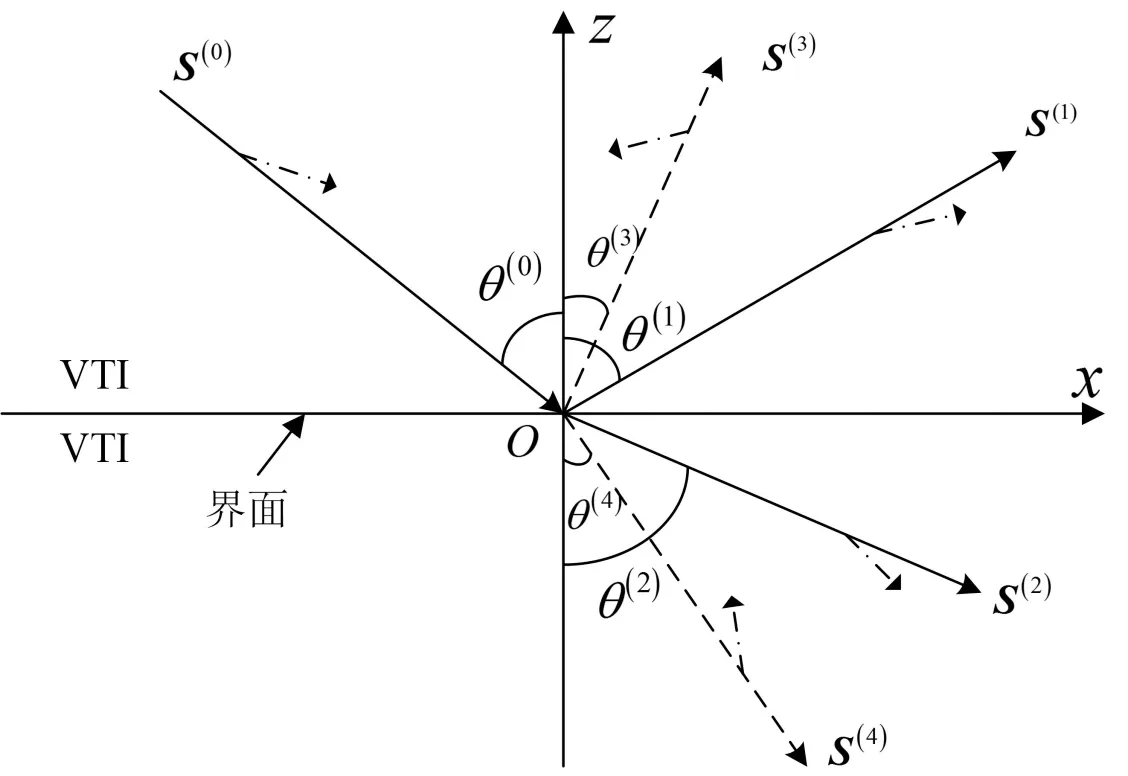
图1 P-波入射VTI-VTI界面示意图

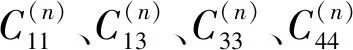
表1 A-页岩和O-页岩的各向异性参数和弹性常数

1.2 异常入射角的证明

异常折射是由于岩石的各向异性所引起的一种物理现象[8]。使用斯奈尔定律来验证异常入射角存在的合理性。在给定的入射角范围内，所有反射和折射波的计算结果都必须满足斯奈尔定律。在入射角等于临界入射角时，必须切换折射P-波的相速度解，其切换方式为

1.2.1 反射角与折射角

基于斯奈尔定律建立了一个4阶多项式[12-13]，以方便求解P-波在VTI-VTI界面处的反射/折射角。使用其相速度的解

(1)

(2)

与其4阶多项式

(3)

(4)

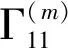
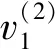
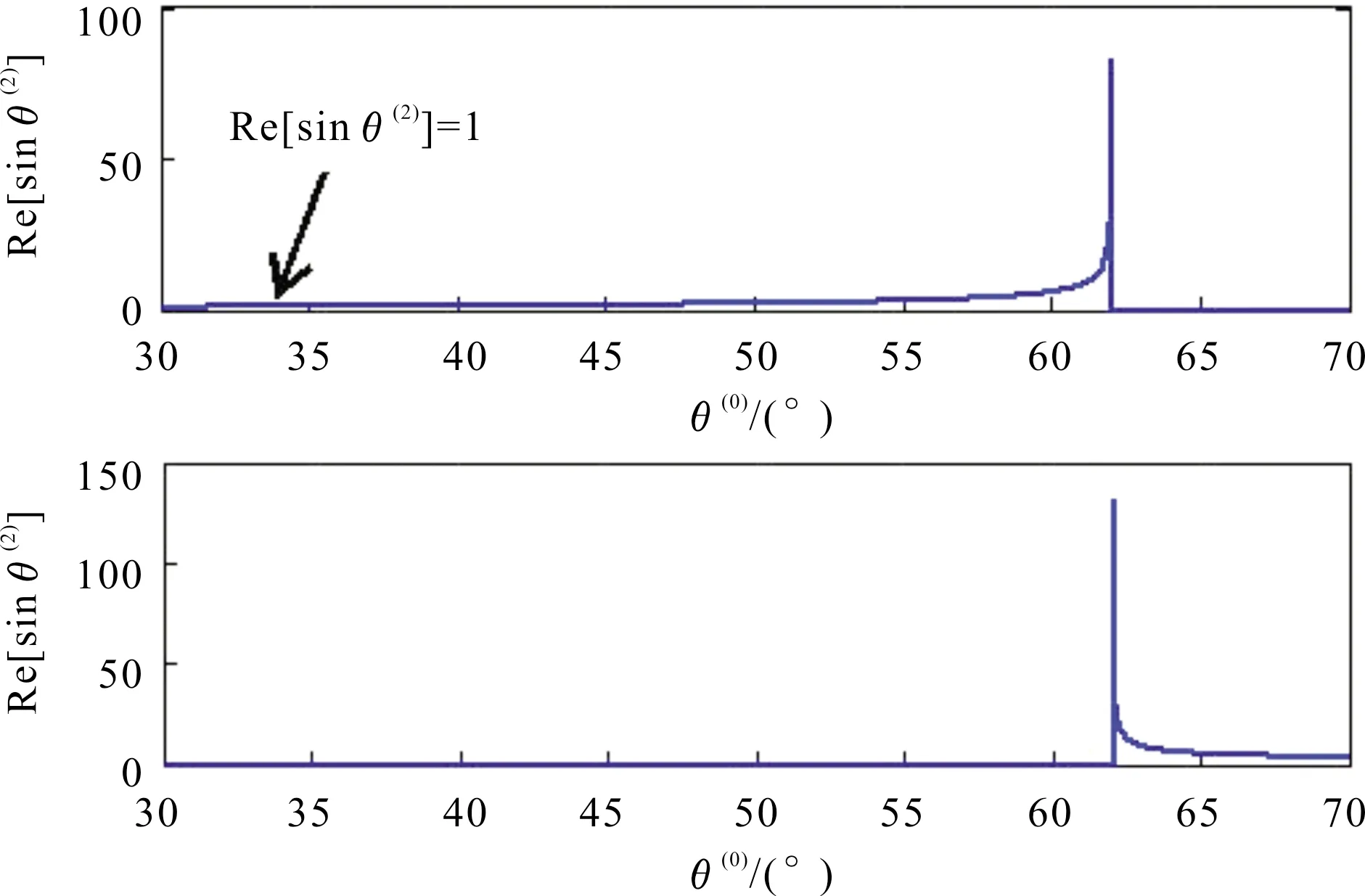
图2 P-波反射角正弦平方与入射角的关系

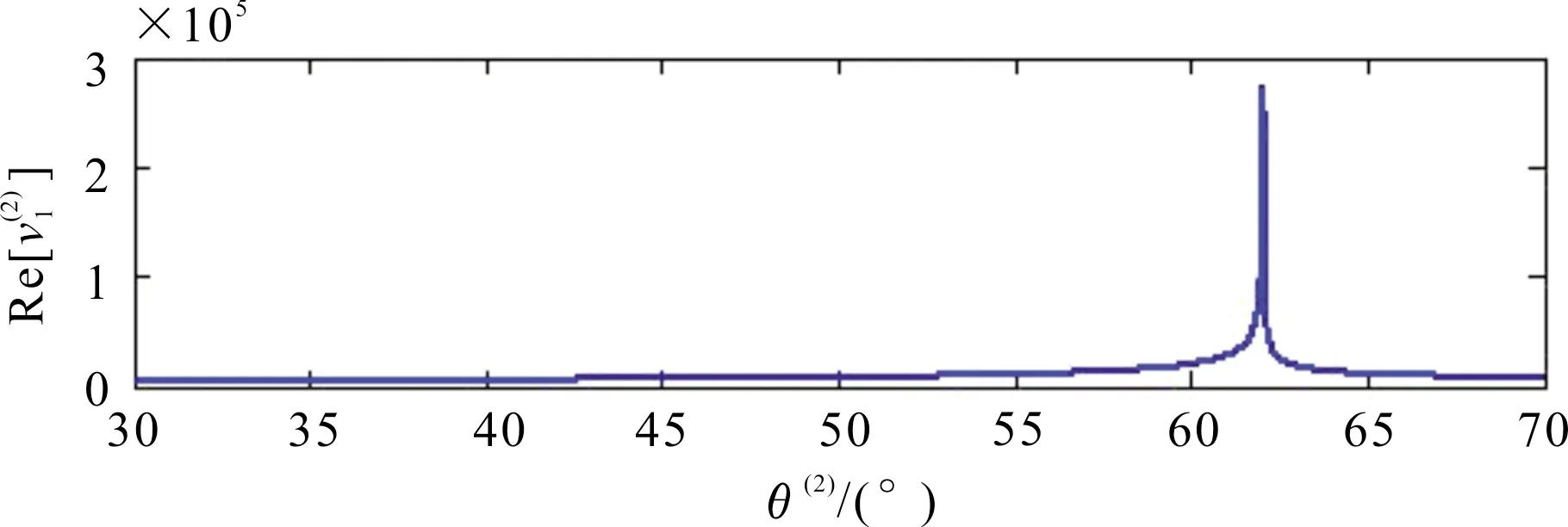
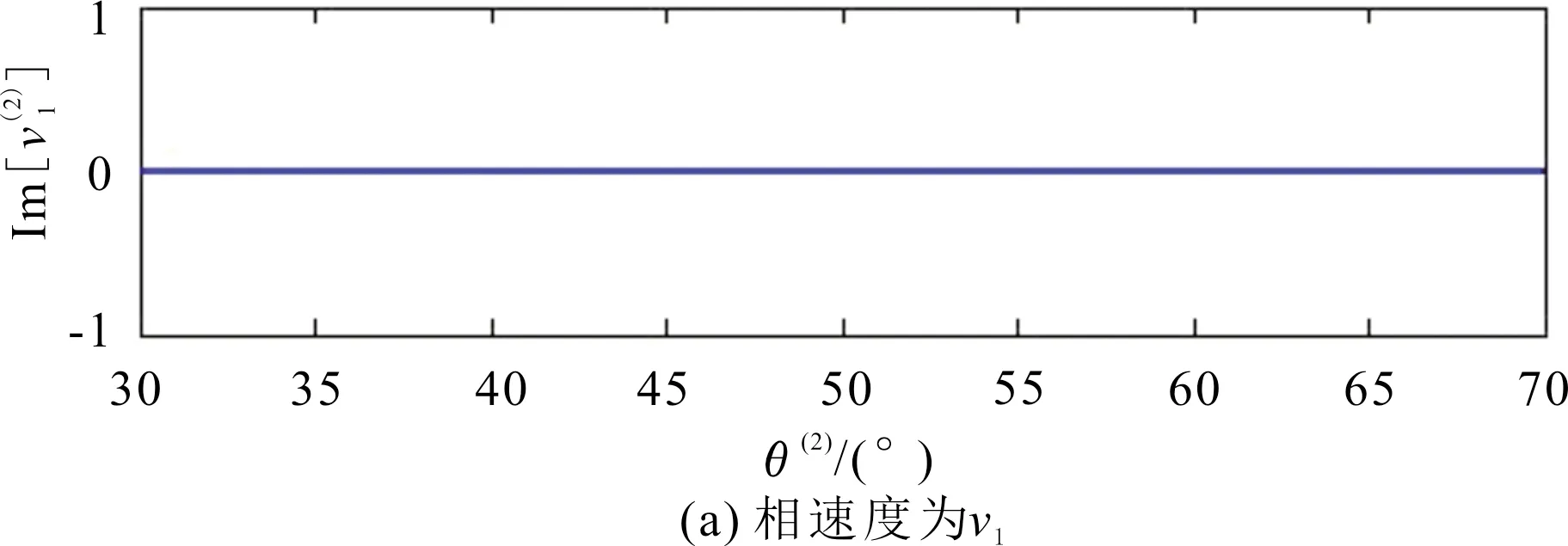
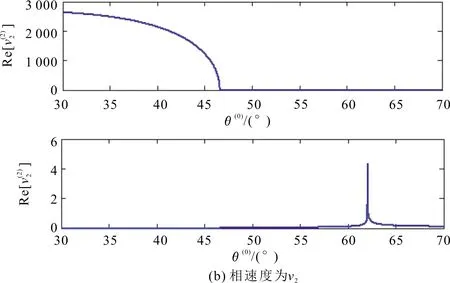
图3 反射P-波相速度与入射角的关系

1.2.2 坡印廷矢量

入射P-波及其模式转换波简化后的Christoffel方程[14]为

根据归一化条件

得到入射P-波在前入射临界角区域产生的均匀折射P-波和其他均匀模式转换波在x-z平面上的极化系数表达式分别为

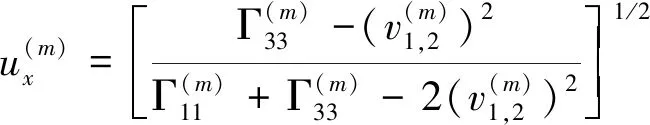
以及在过入射临界角区域产生的非均匀折射P-波在x-z平面上的极化系数表达式分别为

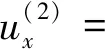
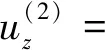
入射波及其模式转换波在x-z平面上的坡印亭矢量表达式为

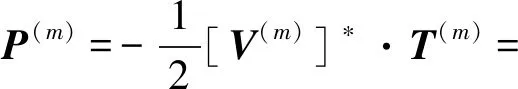
(5)

式中：[V(m)]*表示对应波的质点位移速度的共轭形式；T(m)表示对应波的应力张量。分别将入射波及其模式转换波的质点位移速度和应力张量代入式(5)就可以得到对应波的坡印廷矢量。

由于入射P-波坡印廷矢量的z-分量等于各个模式转换波z-分量的实部之和，因此可以通过能量守恒定律来验证异常入射角的存在。在A-页岩和O-页岩之间的界面上，坡印廷矢量的z-分量与入射角之间的关系如图4所示。图4(a)表示入射P-波坡印廷矢量的z-分量与入射角之间的关系。图4(b)表示各模式转换波的z-分量的实部之和与入射P-波的z-分量与入射角之间的关系，其中，虚线表示入射P-波z-分量的实部之和，实线表示P-波的各模式转换波z-分量实部之和。

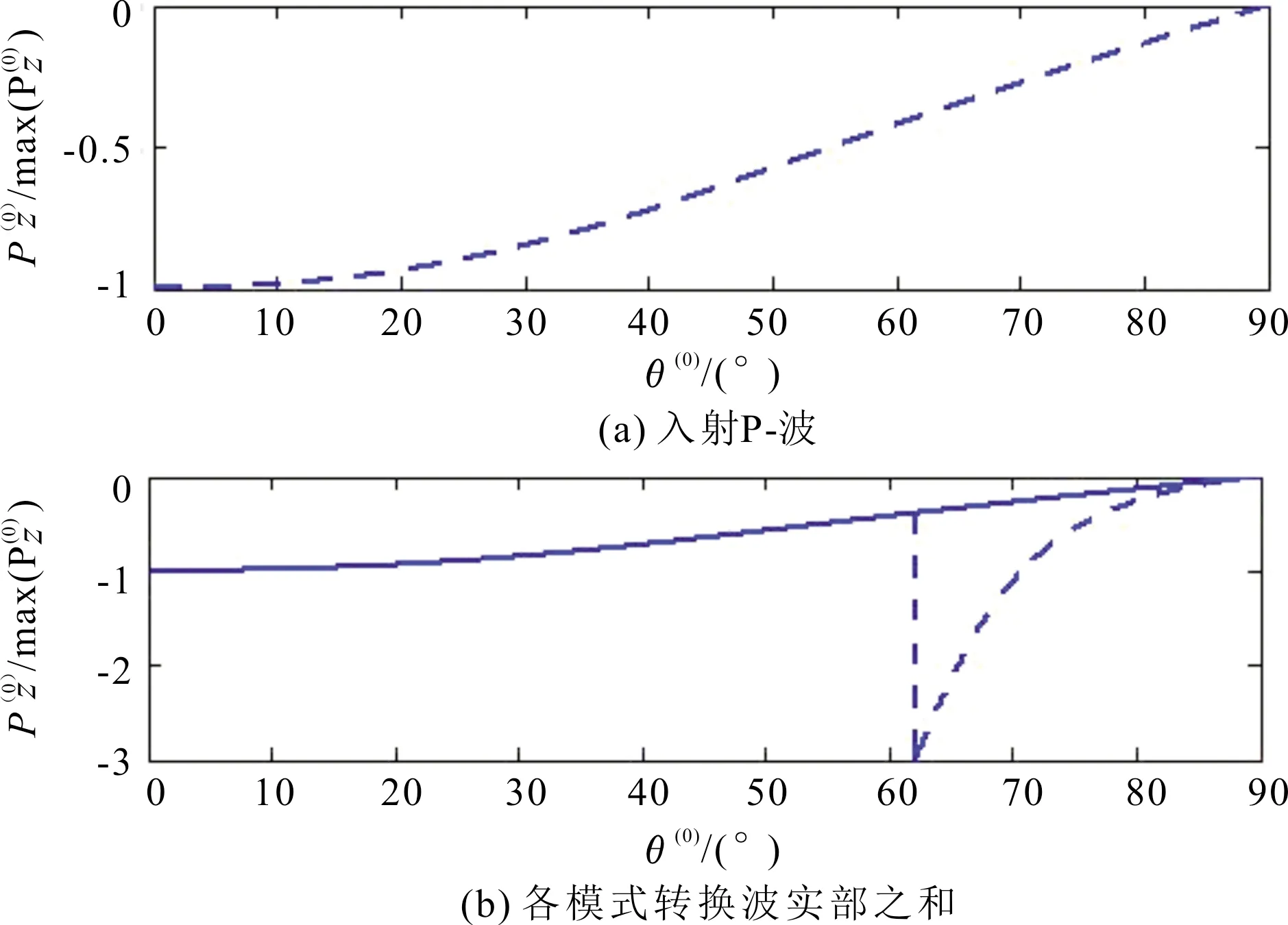
图4 坡印廷矢量的z-分量与入射角关系

2 各向异性岩石的弹性平面波极化

地壳中的岩石介质大多数都会在宏观上表现出强烈的各向异性，而声波的极化会受到岩石中各向异性的影响，下文将对各向异性参数与异常折射角对声波极化的影响进行讨论。

2.1 P-波的极化方向与相速和能速方向的关系

在各向异性岩石中传播的弹性平面P-波或SV-波，通常其质点位移方向不平行P-波或不垂直SV-波的传播方向。平面波的相速度方向通常也不与其传播方向平行。图5描述了在x-z平面中传播的平面P-波特性。图5中的k为波矢量，其方向为相速度方向；P为坡印廷矢量，其方向为P-波的传播方向；u为归一化的质点位移矢量，也被称为平面波的极化矢量，其方向为P-波的极化方向，它的x-分量和z-分量称为极化系数。相角θ的定义为波矢量与z轴的夹角，能角φ的定义为坡印廷矢量与z轴的夹角，极化角ξ的定义为极化矢量与z轴的夹角。

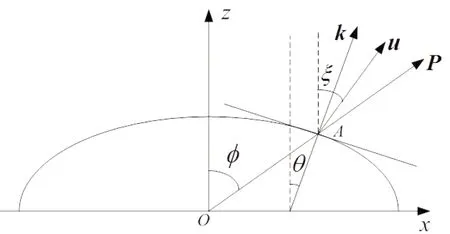
图5 x-z平面中传播的平面P-波特性示意图

对于在各向异性岩层中沿相同方向传播的P-波和SV-波，在任意一空间位置，两者的极化方向相互垂直[14]，因此，只要知道了平面P-波的极化方向也就知道了平面SV-波的极化方向。对坡印廷矢量和极化系数进行分析，可以得到能角、极化角与相角之间的相互关系为

其中，

Γ13=Γ31=(C13+C44)sinθcosθ/ρΓ33=(C33cos2θ+C44sin2θ)/ρ

能速与相速度的关系[10]可写为

ve=v/cos(φ-θ)

式中，v可以表示P-波的相速度，也可以是SV-波的相速度。

极化角ξ与相角θ的差以及极化角ξ与能角φ的差可以分别可表示为

Δθ=ξ-θ

(6)

Δφ=ξ-φ

(7)

选取4种不同岩石样品的各向异性参数和物理参数如表2所示。表2中α和β分别表示P-波和SV-波在介质的对称轴方向上的相速度，ε和δ*分别为介质的各向异性参数，ρ为介质的密度。

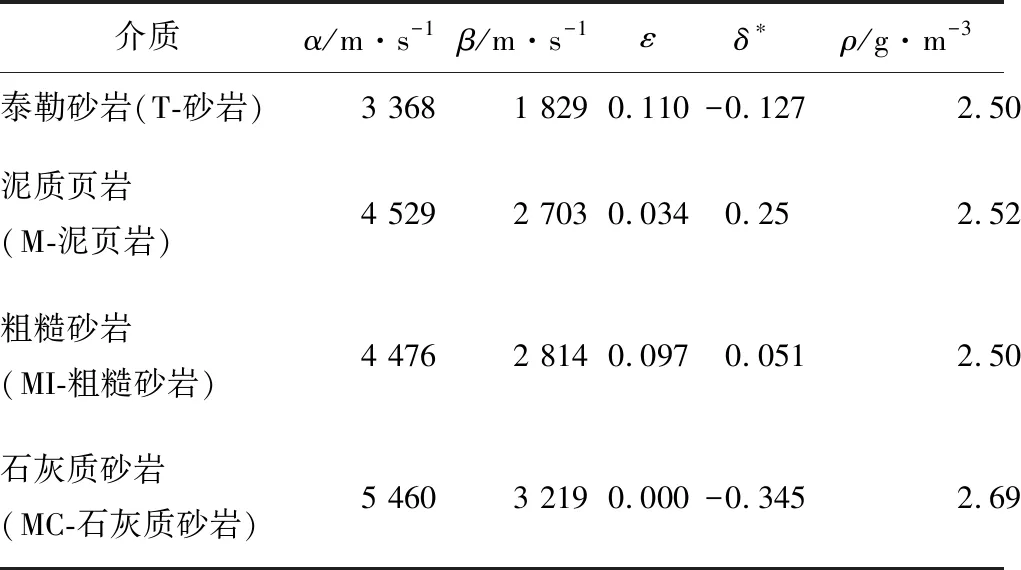
表2 4种岩石样品各向异性参数

依据表2中给出的4种岩石样品的参数结合式(6)、式(7)能够计算4种岩石样品Δθ和Δφ与相角θ以及能角φ的关系，计算结果如图6—图9所示。图中的实线分别表示Δθ和Δφ与θ之间的关系，虚线分别表示Δθ和Δφ与θ及φ的关系。由图6—图9可知，平面波在VTI介质内传播，其极化方向会偏离相速度方向和能速方向，偏离角的大小由各向异性岩石的物理参数、各向异性参数以及P-波的传播方向共同决定。

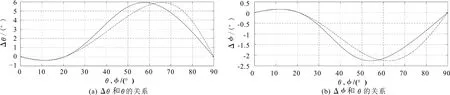
图6 泰勒砂岩Δθ和Δφ与θ及φ的关系

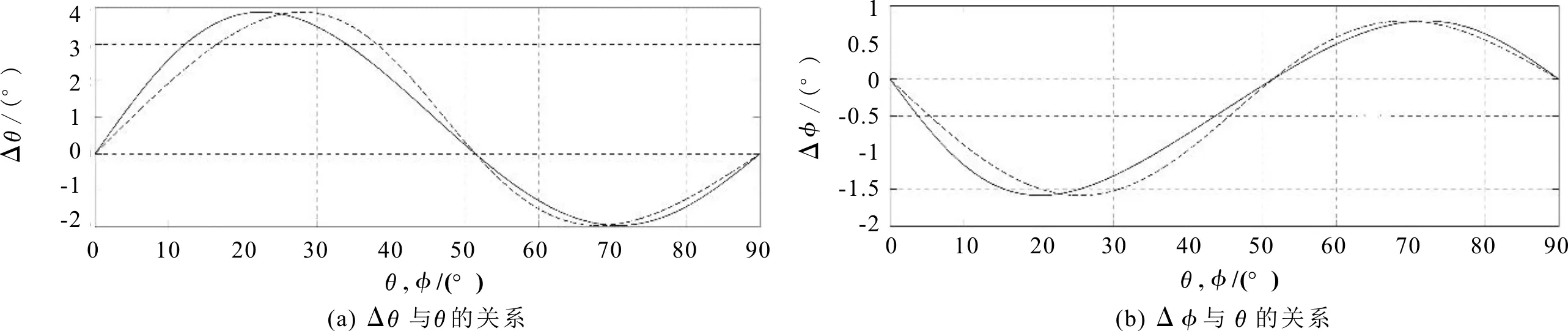
图7 泥质页岩Δθ和Δφ与θ及φ的关系

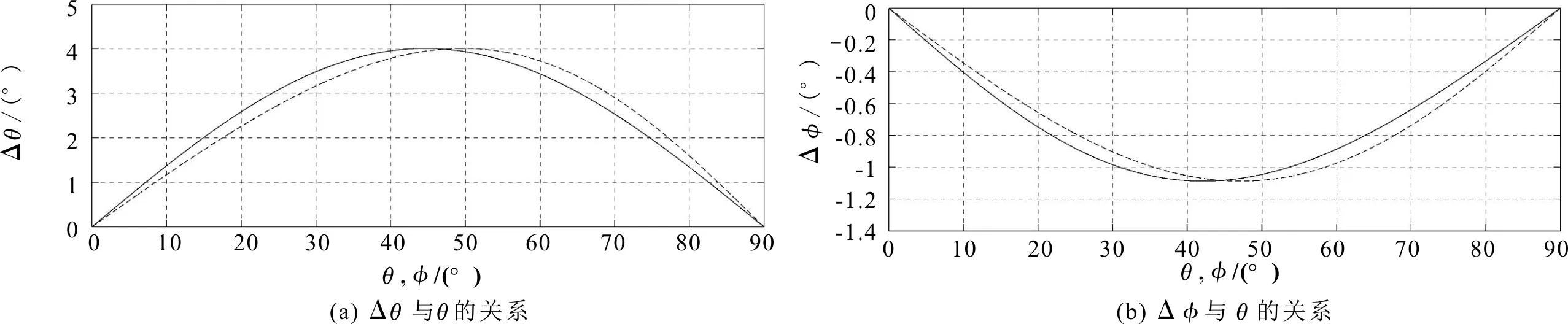
图8 粗糙砂岩Δθ和Δφ与θ及φ的关系

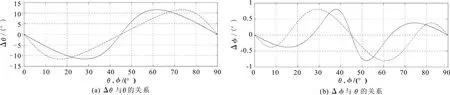
图9 石灰质砂岩Δθ和Δφ与θ及φ的关系

2.2 折射P-波的椭圆极化状态

入射P-波和在VTI-VTI界面上产生的模式转换波的极化状态，不但与入射/折射介质的各向异性参数和物理参数有关，还与入射角有关。可以通过观测非均匀折射P-波的椭圆极化状态来判断各向异性岩石界面是否存在异常入射角[15-16]。通过研究两个界面模型来进行分析讨论。其中，模型一为不存在异常入射角的A-页岩/T-砂岩界面模型，模型二为存在异常入射角的A-页岩/O-页岩界面模型。

对于非均匀折射P-波，极化系数的z-分量的相位滞后于x-分量，存在90°的相位差，旋转方向符合左手螺旋法则，为左旋椭圆极化波；极化系数的z-分量的相位超前于x-分量，旋转方向符合右手螺旋法则，为右旋椭圆极化波[17]。

式中，

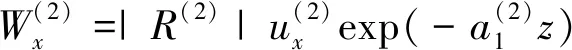
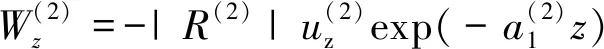
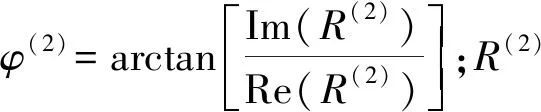
式中，

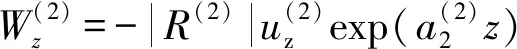
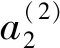
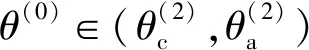
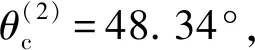
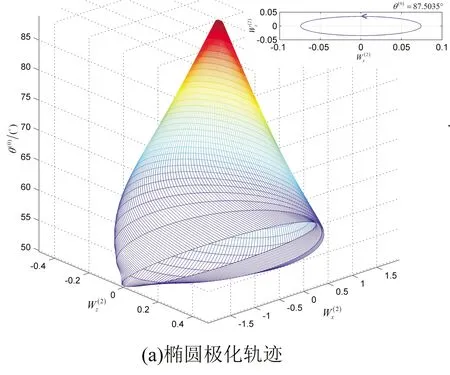
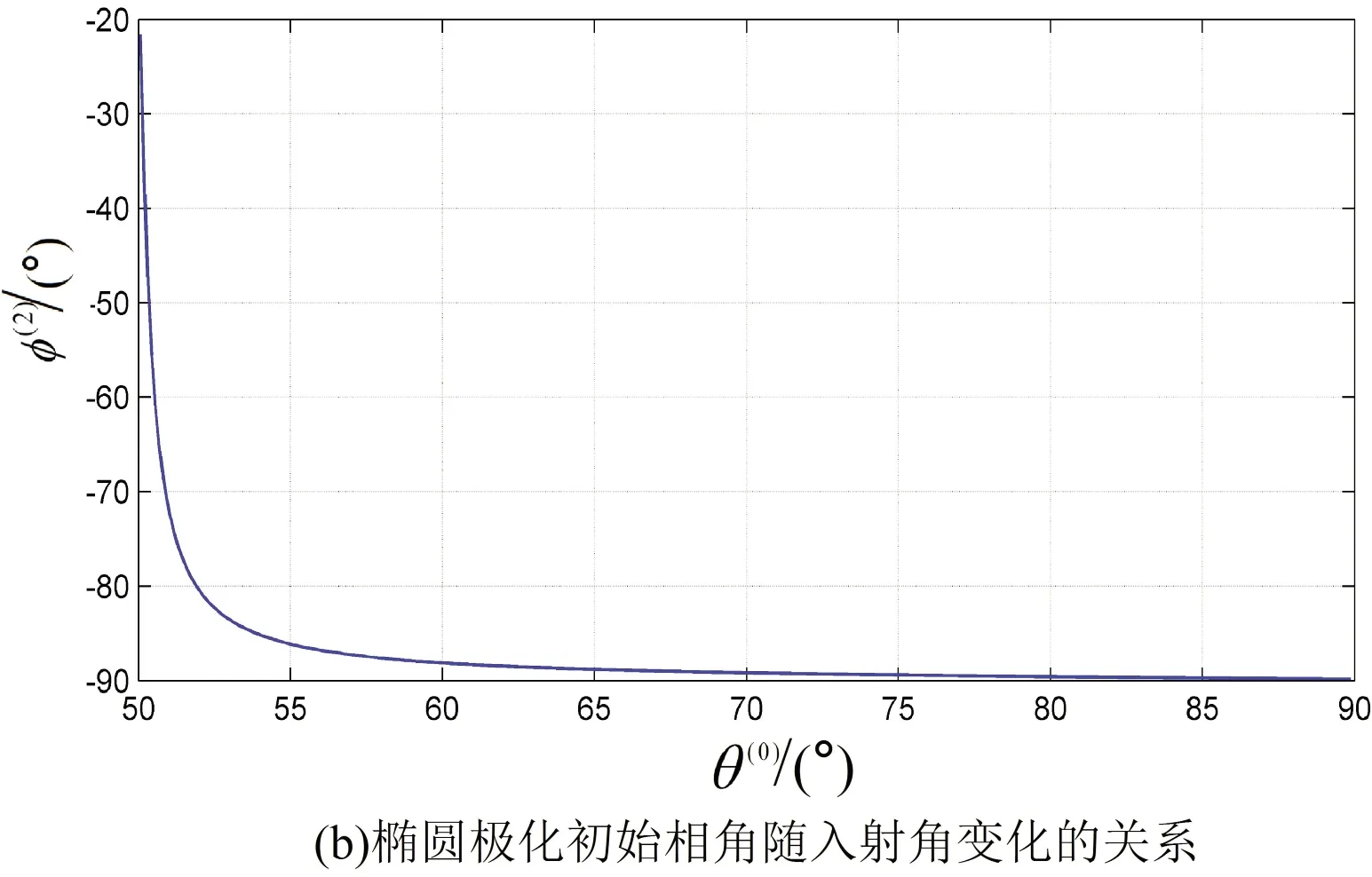
图10 模型一非均匀折射波的极化状态与入射角的关系

2.3 各向异性对线性极化波极化方向的影响

针对在泥质页岩中传播的均匀平面P-波，分析岩石各向异性参数ε和δ*对线性极化P-波的极化方向的影响。保持δ*不变，ε取值的范围为-0.1～0.1，计算出的线性极化P-波的极化方向偏离相速/能速方向的角度与各向异性参数ε和入射角θ之间关系如图12所示。保持ε不变，δ*取值的变化范围为-0.25～0.25，计算出的线性极化P-波的极化方向偏离相速/能速方向的角度(Δθ/Δφ)与各向异性参数δ*和入射角θ之间关系如图13所示。观察图12和图13可知，线性极化P-波的极化方向不仅取决于其传播方向θ和φ，还取决于岩石的各向异性参数δ*和ε。

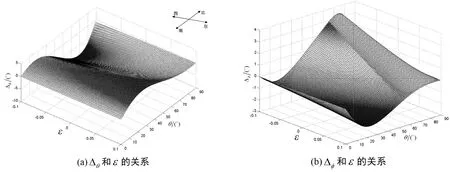
图12 泥质页岩介质中Δθ、Δφ和ε的关系

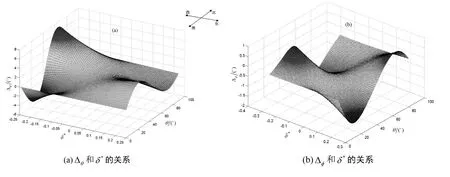
图13 泥质页岩介质中Δθ、Δφ和δ*的关系

2.4 各向异性对非均匀折射波极化状态的影响

分别选择入射介质和折射介质的各向异性参数作为变量，分析这些参数对在各向异性岩石界面上产生的非均匀折射P-波的椭圆极化状态的影响。

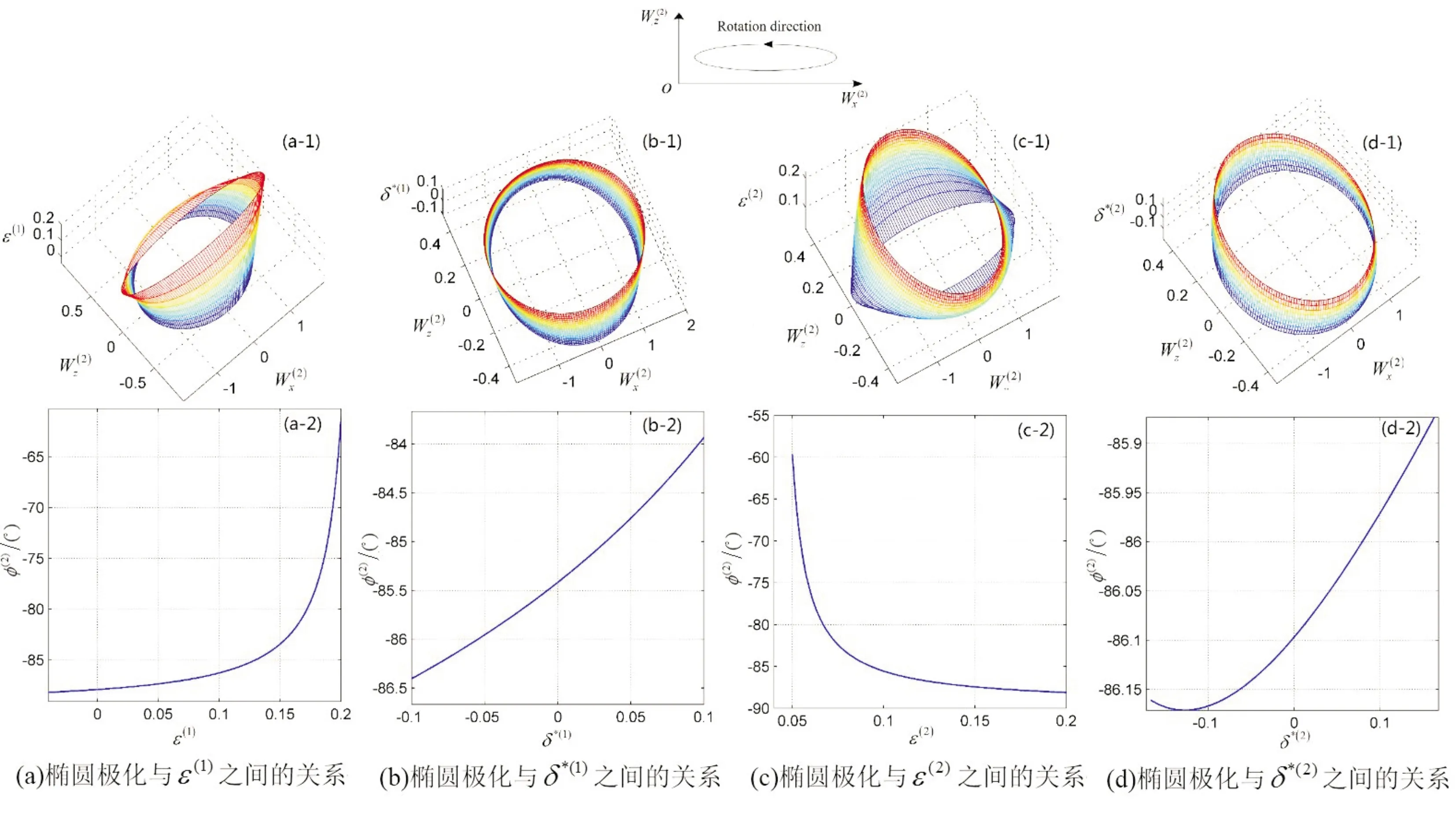
图14 模型一界面上非均匀折射波椭圆极化状态与各向异性参数之间关系

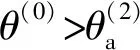
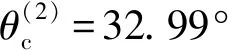
图15 模型二界面上非均匀折射波椭圆极化状态与各向异性参数之间关系

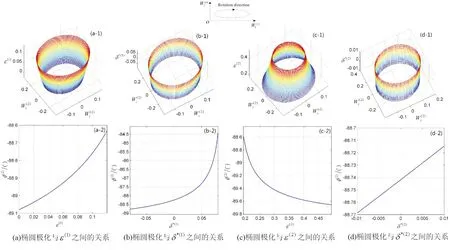
图16 模型二界面上非均匀折射波椭圆极化状态与各向异性参数之间关系

3 压电换能器的能量转换网络模型

压电换能器之所以能够将电信号和声信号相互转换，是因为压电材料具有良好的机电转换能力，可以实现电能-机械能/机械能-电能的有效转换[5]。最常见的压电换能器几何结构有球形、圆柱形和片状等，现已广泛应用于石油测井、工业测量等工业领域中。

3.1 声学传输网络模型

激励声源压电换能器的电压驱动信号子波通常由多个不同频率、初相位和幅度的正弦信号构成。电压驱动信号子波可以离散为许多个不同频率、初相位和幅度的正弦频率分量。对于简谐振动的压电换能器，其辐射阻和辐射质量是频率的函数。因此，基于线性叠加原理，多频电压驱动信号子波激励声源压电换能器的过程可以等效为一个并联的电-声传输网络，声波测量过程中的传输网络示意图如图17所示。其中，U(t,ω)表示t时刻角频率为ω的一个电压驱动信号，UN(t,ω)表示为电压驱动信号U(t,ω)经过离散后的第N个子波信号，hN(t,ωN)第N个子波信号对应的电-声冲激响应信号，ωN表示第N个子波信号对应的电-声冲激响应信号的角频率，vN(t,ωN)表示为第N个子波信号经过机电网络后的卷积输出，v(t)表示为声源压电换能器向外辐射的声波信号子波，Uj是电驱动信号中的第j个频率分量，ωj表示第j个频率分量的角频率。利用留数定理求解压电换能器的单频电-声冲激响应，得到过阻尼、临界阻尼和欠阻尼震荡3种不同的震荡模式。

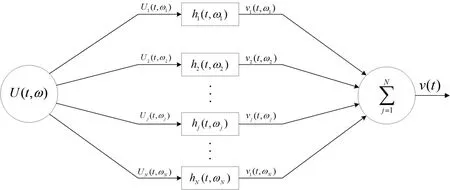
图17 声波测量过程中的传输网络示意图

从压电材料的物理性质来看，欠阻尼模式对应的解才是具有实际的物理意义的解，其第j个频率分量的电-声冲激响应信号的表达式可写为

hj=Ajexp[-αjt]+Bjexp[-βjt]cos(ωjt+φj)

式中，Aj、Bj、αj、βj和φj分别表示第j个频率分量的相关的系数。

声源压电换能器向外辐射的声信号子波的第j个频率分量，即电压驱动信号子波的第j个频率分量和第j个等效电路的电-声冲激响应的卷积输出，可写为

vj(t)=Uj(t)hj(t)

式中，Uj(t)表示第j个频率分量的信号子波。所以，声源压电换能器向外辐射的声波信号子波是所有并联电路输出的累加和，可写为

3.2 薄球壳换能器

薄球壳压电换能器的几何结构示意图如图18所示。其中，薄球壳压电换能器的薄壳厚度为lt，球壳内表面半径为r0，外表面半径为r1。令薄球壳压电换能器平均半径为rb，由于球形半径远大于壳体厚度，所以有近似关系r0≈rb≈r1其中rb=(r0+r1)/2，并且为径向极化，电极分别是其内表面和外表面。

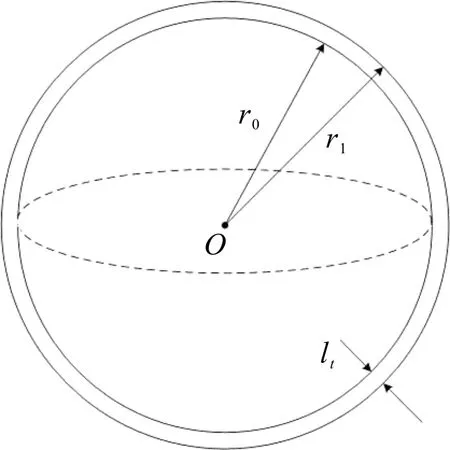
图18 薄球壳压电换能器的示意图

理论仿真和实际测量的接收换能器输出归一化电信号波形如图19所示。其中，图19(a)为幅度谱波形图，图19(b)为频域波形图。实线为理论仿真结果，虚线为实际测量结果。理论计算认为声源和接收换能器被放置在无限大的水池中；实际测量中声源换能器和接收换能器被放置在较大且消声的水池中。理论仿真与实际测量结果均消除了池壁反射波的影响。从整体上看，网络模型的计算结果与实验观测结果吻合较好。将实际测量信号与声学传输网络模型仿真所得结果进行对比，可以看出实际测量信号的幅度谱向低频有轻微的偏移，误差约为0.77%。这是由于现实中水具有一定的粘度，这可能会导致声信号在传播过程中衰减。

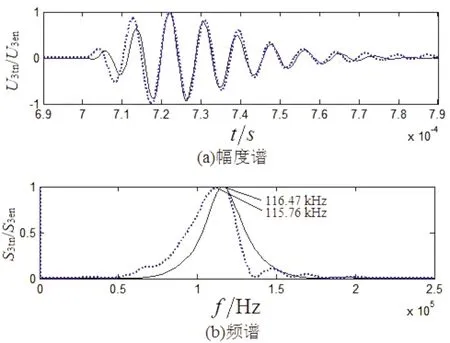
图19 接收换能器输出的归一化电信号波形图

4 结论

通过对具有各向异性的两个不同沉积岩层所组成的界面进行分析，建立了一个4阶多项式来计算反射角和折射角，并通过计算界面模型入射波及其模式转换波的坡印廷矢量z-分量满足能量守恒定律，得到异常入射角是存在的这一结论。在此之后研究了各项异性参数对极化方向与极化轨迹的影响，并分别对存在异常入射角和不存在异常入射角的两个模型界面建立椭圆极化方程，分析异常入射角对极化状态的影响。最后研究了换能器的传输过程，建立了能量转换并行传输网络模型。通过研究，得到以下结论。

1)异常入射角存在是合理的，且在异常入射角处折射P-波相速度的两个解必须切换，否则计算出的结果不能满足能量守恒定律。

2)平面波在VTI介质中传播，其极化方向会偏离相速度方向和能速方向，偏离角的大小由各向异性岩石的物理参数、介质的各向异性参数以及P-波的传播方向共同决定。

4)椭圆极化轨迹方程的大小，形状和初始相角不仅仅与入射角有关，而且还与入射介质和折射介质的各向异性参数有关。

5)压电换能器的并联传输网络模型能够较好地描述声源换能器在电压驱动信号的激励下向外辐射的声波信号子波，很好地诠释了压电换能器声-电转换过程中换能器特性和电压驱动信号子波特性对辐射的声波信号子波的影响。