改进粒子群算法的D2D功率分配

张继荣，孟繁克，王晟寰

(1.西安邮电大学 继续教育学院，陕西 西安 710061; 2.西安邮电大学 通信与信息工程学院，陕西 西安 710121；3.北京市第三十五中学，北京 100035)

随着智能终端的普及和无线数据业务的快速增长，对第5代移动无线网络(5th Generation Mobile Wireless Network，5G)能否满足大量用户各类通信需求提出了巨大挑战[1]。终端直通通信(Device-to-Device，D2D)作为5G的关键技术之一，具有扩大信号的覆盖范围，降低传输时延等优势，从而可以使边缘用户的性能得到提高。D2D用户间的距离较近，可以节约电池的电量[2]。D2D用户复用蜂窝用户的频谱资源有正交和非正交两种模式，当采用正交模式时，D2D用户与蜂窝用户之间不存在同频干扰，但是，正交模式的频谱利用率较低。当采用非正交模式时，虽然可以有效提高频谱效率，降低蜂窝网络的负载。然而，非正交模式也为D2D用户和蜂窝用户之间带来了同频干扰问题[3-5]。功率分配是减少无线网络中干扰的有效方法[6]，合理的功率分配算法可以有效提高网络的性能。

在相关的研究中，文献[7]提出了固定的功率分配策略，与无功率控制方法相比，该策略能够有效提升用户总体吞吐量，但是没有考虑到边缘用户的发送功率。文献[8]提出一种基于D2D用户群组划分，同时考虑D2D用户和蜂窝用户相互干扰的功率控制方法。虽然该方法能有效提高吞吐量，但是该方法只是保证了蜂窝用户的通信质量，没有保证D2D用户的通信质量。文献[9]采用速率最大化，从而得到最优功率分配，但是其仅仅保证了蜂窝用户的通信质量(Quality of Service,QoS),没有考虑到D2D用户的QoS。

针对D2D用户和蜂窝用户间存在同频干扰的问题，拟提出一种以最大化蜂窝用户和D2D用户的整体吞吐量为目标的改进粒子群(Particle Swarm Optimization，PSO)功率分配算法。将粒子的位置坐标值类比为用户的发送功率，通过迭代寻优，最终为粒子分配最优的发送功率。通过为每个用户分配最佳的发送功率，以减小D2D用户和蜂窝用户之间的同频干扰。

1 系统模型

假设基站具有所有链路的完美信道状态信息，所研究的是D2D用户复用蜂窝用户的上行链路频谱资源，相对于下行链路频谱资源，其资源利用率较低，同时基站处理干扰的能力较强，可以很好地处理D2D用户对蜂窝用户的干扰[10-13]。假设在已经确定好每一个D2D用户对的发送端和接收端在小区中的位置分布的前提下，一个D2D对只能复用一个蜂窝用户(Cellular User，CUE)的上行信道，一个CUE的上行信道可以被多个D2D对复用。在模型中，基站(Base Station，BS)位于小区的中心，{D2D1,D2D2,D2D3,D2D4……D2Di……D2Dn}表示小区中的D2D用户对，{CUE1,CUE2,CUE3,CUE4……CUEj,……CUEm}表示小区中的蜂窝用户,其中m，n分别是蜂窝用户和D2D用户对的个数，0≤i≤n,0n。单小区通信模型如图1所示。

图1 单小区通信模型

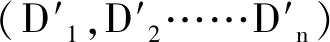
当D2D对复用蜂窝上行链路资源时，D2D发送端发送的信号将对基站产生干扰，所以第j个蜂窝用户在基站端的信干噪比(Signal to Interference Plus Noise，SINR)可以表示为

(1)

式中：PC,j表示第j的蜂窝用户的发送功率；Gj表示第j的蜂窝用户到基站间的增益；ρji表示复用因子，当ρji=1时，表示D2D用户复用蜂窝用户的资源，当ρji=0时，表示不存在复用关系；PD,i表示第i个D2D对的发送功率；Yi表示第i个D2D对到基站间的增益；σ2表示加性高斯白噪声的功率。

第i个D2D对的接收端的信干噪比可以表示为

(2)

式中：Gi表示D2D对之间的链路增益；Gji表示第j个蜂窝用户与第i个D2D对之间的链路增益。

根据香农公式可以计算蜂窝用户的吞吐量为

RC,j=Blog2(1+RSIN,j)

(3)

其中，B为资源块的带宽。

D2D用户的吞吐量表示为

RC,i=Blog2(1+RSIN,i)

(4)

用户间的链路增益为

G=χL|h|2

(5)

其中：χL为用户间的路径损耗，|h|2为信道影响因子。

D2D用户间和蜂窝用户到基站间的路径损耗[14]表达式为

(6)

(7)

其中：dDD为D2D对之间的距离；dDB为D2D发送端与基站的距离;dCB为蜂窝用户到基站间的距离。

蜂窝用户和D2D用户总的吞吐量为

(8)

以吞吐量最大为目标建立优化模型，优化模型的目标函数为

(9)

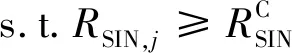
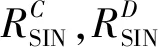
2 改进粒子群功率分配算法

为了求解式(9)的优化模型，将从功率分配的角度进行优化，将粒子群算法中粒子的位置类比为D2D用户和的蜂窝用户的发送功率，通过粒子群算法的迭代寻优，找出粒子的全局最优位置，即D2D用户和蜂窝用户的发送功率。假设在一个(m+n)维的目标搜索空间中，有N个粒子组成一个部落，那么第u个粒子的位置表示为一个(m+n)维的向量为

Xu=(xu1,xu2,…,xu(m+n))

u∈1,2,…,(m+n)

第u个粒子的“飞行”速度也是一个(m+n)维的向量，表示为

Vu=(vu1,vu2,…,vu(m+n))

第u个粒子迄今为止搜索到的最优位置，也就是个体极值，表示为

Pb=(Pu1,Pu2,…,Pu(m+n))

整个粒子群迄今为止搜索到的最优位置，也就是全局极值，表示为

P′g=(P′u1,P′u1,…,P′u(m+n))

每次迭代粒子都会更新自己的速度和位置，其表达式分别为

(10)

xu(m+n)(t+1)=xu(m+n)(t)+Vu(m+n)(t+1)

(11)

其中：c1和c2为学习因子，也称为加速常数；r1,r2为[0,1]范围内的均匀随机数；t为当前的迭代次数；w(t)为第t次迭代时的惯性权重；Pb(t)和P′g(t)分别表示第t次迭代时的个体极值和全局极值。

2.1 惯性权重比较

1)线性递减惯性权重，其表达式[15]为

(12)

式中：wmax值为0.9；wmin值为0.2；t为当前迭代次数；Nmax为最大迭代次数。算法在初期具有较强的搜索能力，并且在后期能够得到相对精确的结果。但是，其只有在全局最优点附近时才有效，如果在算法的初始阶段找不到全局最优点，随着惯性权重的递减，局部搜索能力会逐渐增强，那么算法会跳过全局最优点，逐渐陷入局部最优。

2)线性微分递减惯性权重，其表达式[16]为

(13)

式中：ws为迭代初始是的惯性权重值，大小为0.2；we为迭代结束时的惯性权重值，大小为0.9。该算法在迭代初期，惯性权重的下降趋势缓慢，全局搜索能力强，有利于找到很好的粒子，在算法进化后期，惯性权重的减小趋势加快，一旦在前期找到全局最优值，可以使得算法收敛速度加快。但是，较小的惯性权重值会导致粒子可能陷入局部极值。

3)所提基于递减指数函数的惯性权重表达式为

(14)

递减指数函数的惯性权重在前期有较大的惯性权重值，有助于粒子在较大优化空间寻找最优解，全局搜索能力强，有助于粒子跳出局部极值，在进化的后期，保持较小的惯性权重，有利于局部搜索，加速算法的收敛。

为了对比3种算法的迭代性能，选用两个基准测试函数Griewank函数和Rastrigin函数对3种惯性权重进行测试，测试种群大小为40，其他测试参数与下文一致。

1)Griewank函数

(15)

-100≤xu≤100

式中：xu为第u个粒子的位置；f(x)为第u个粒子函数值；Nmax为粒子最大迭代次数。Griewank函数具有大量局部极值点的不可分离的多峰函数，有一个全局极小点x*=(0,0,…,0)，函数的最优值为f(x*)=(0,0,…,0)。10维和40维的测试结果分别如图2和图3所示。

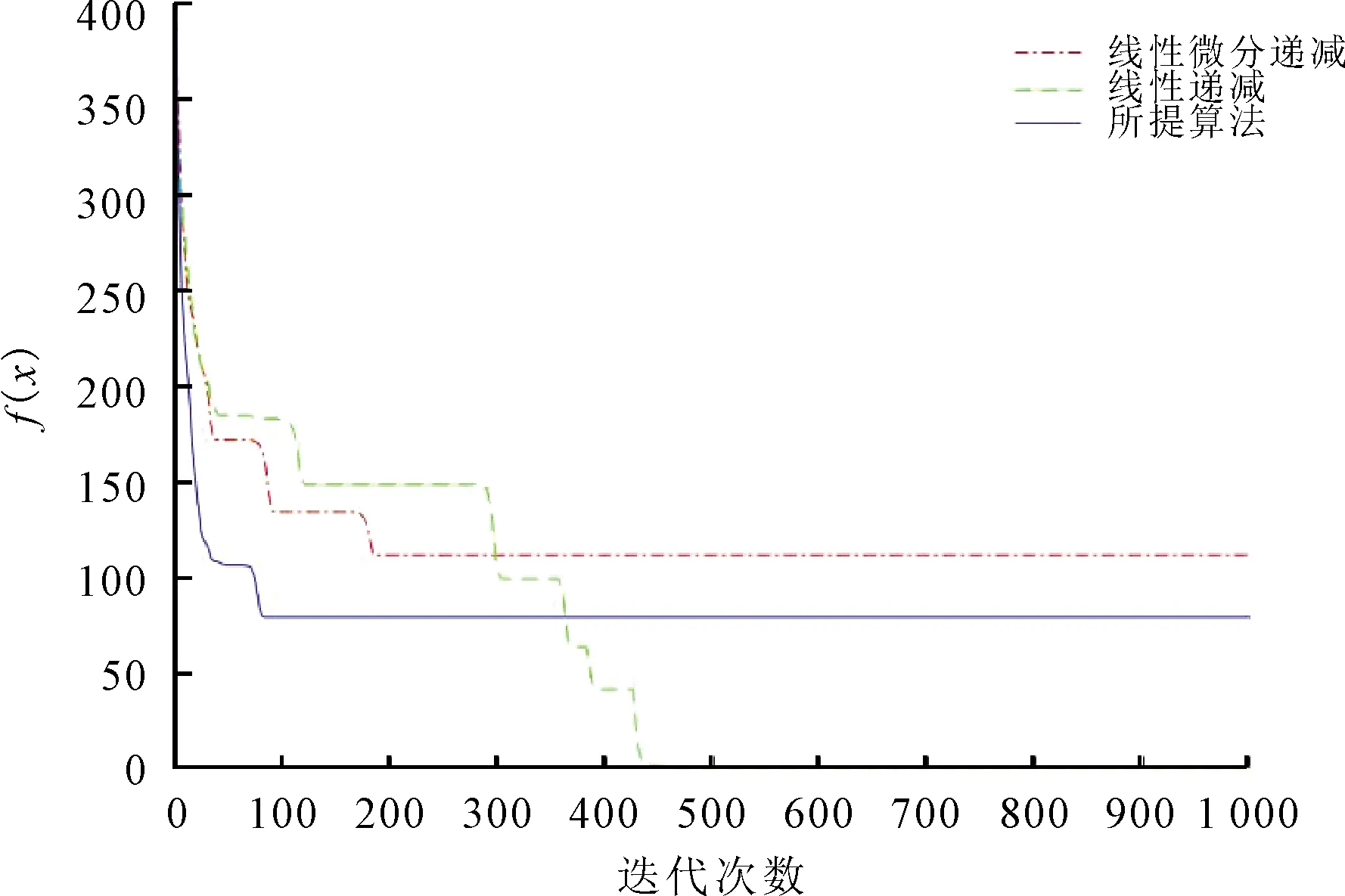
图2 10维测试结果

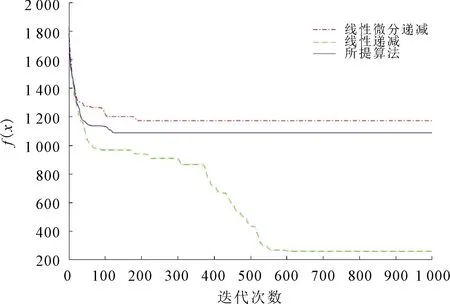
图3 40维测试结果

由图2可以看出，所提算法在第80次收敛，所需要的时间为1 s，线性微分递减函数在第190次时达到收敛，所需时间为2 s，线性递减则需更多。从图3中可以看出，所提的策略在120次的迭代次数下结果就达到了最优，所需要的时间为1.5 s，在实际的应用中节省了时间。

2)Rastrigin函数

(16)

-10≤xu≤10

参数含义与式(15)一样，Rastrigin函数也是有大量局部最优点的多峰函数，其有一个全局最优点x*=(0,0,…,0)，函数的最优值为f(x*)=0。10维和40维的测试结果分别如图4和图5所示。

图4 10维测试结果

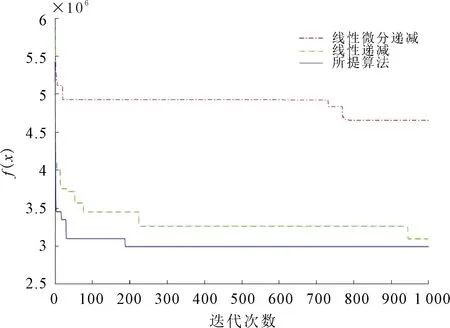
图5 40维测试结果

通过图4可以看出，在10维时所提基于递减指数的惯性权重在第100次迭代时就收敛，所需时间为1 s，而其他两种惯性权重收敛时的迭代次数均大于所提算法，所提惯性权重的整体寻优能力和寻优结果均好于线性微分递减的惯性权重和线性递减的惯性权重。图5中可以看到在40维时，所提的惯性权重在190次就迭代到最优，所需时间为1.7 s，收敛速度明显优于其他两种惯性权重。

2.2 算法的实现步骤

步骤1初始化两个大小为N×(n+m)的矩阵，N为粒子数，(n+m)为蜂窝用户和D2D用户数之和，初始化最大的迭代次数Nmax。

步骤2让t从1开始迭代，将用户的发送功率类比为粒子的位置，并随机分布粒子的位置为

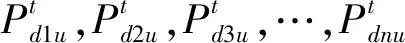
速度为

步骤3根据式(9)计算每个粒子的适应度值。

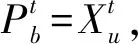
步骤5迭代次数t=t+1。

步骤6通过式(10)更新粒子的速度。

步骤7通过式(11)更新粒子的位置。

步骤8计算新的适应度的值。

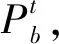
3 仿真与分析

3.1 仿真参数

仿真场景为单小区蜂窝上行通信链路，蜂窝用户和D2D用户之间的资源复用关系为D2D用户复用蜂窝用户的频谱资源。D2D用户最大间距选取50 m，过大的间距将影响D2D用户的通信性能，每个D2D复用的CUE资源带宽为15 kHz。在进行粒子群算法参数的选取方面，文献[16-19]通过实验或者进行了理论分析，推荐了一组固定参数值。仿真参数设置如表1所示。

表1 仿真的主要参数

续表1 仿真的主要参数

3.2 性能比较

分别对比改进PSO算法与固定功率分配算法和随机功率分配算法的性能仿真结果如图6所示。

图6 总吞吐量与D2D对之间的距离关系

从图6可以看出，系统总吞吐量与D2D对之间的距离关系，总吞吐量随着D2D对之间距离的增大而减小，相比于随机功率分配和固定功率功率分配算法，所提算法的总吞吐量在D2D用户间的距离从5～45 m始终高于其他两种算法，表明所提算法具有更好的性能，随机功率分配算法和固定功率分配算法的吞吐量相差不是很大，在25～45 m之间，随机功率分配算法的随机性导致固定功率分配算法的吞吐量高于随机算法。随着D2D用户间距离的增大，其路径损耗也在随着增大，用户所受到的干扰也增大，导致吞吐量呈递减的趋势。

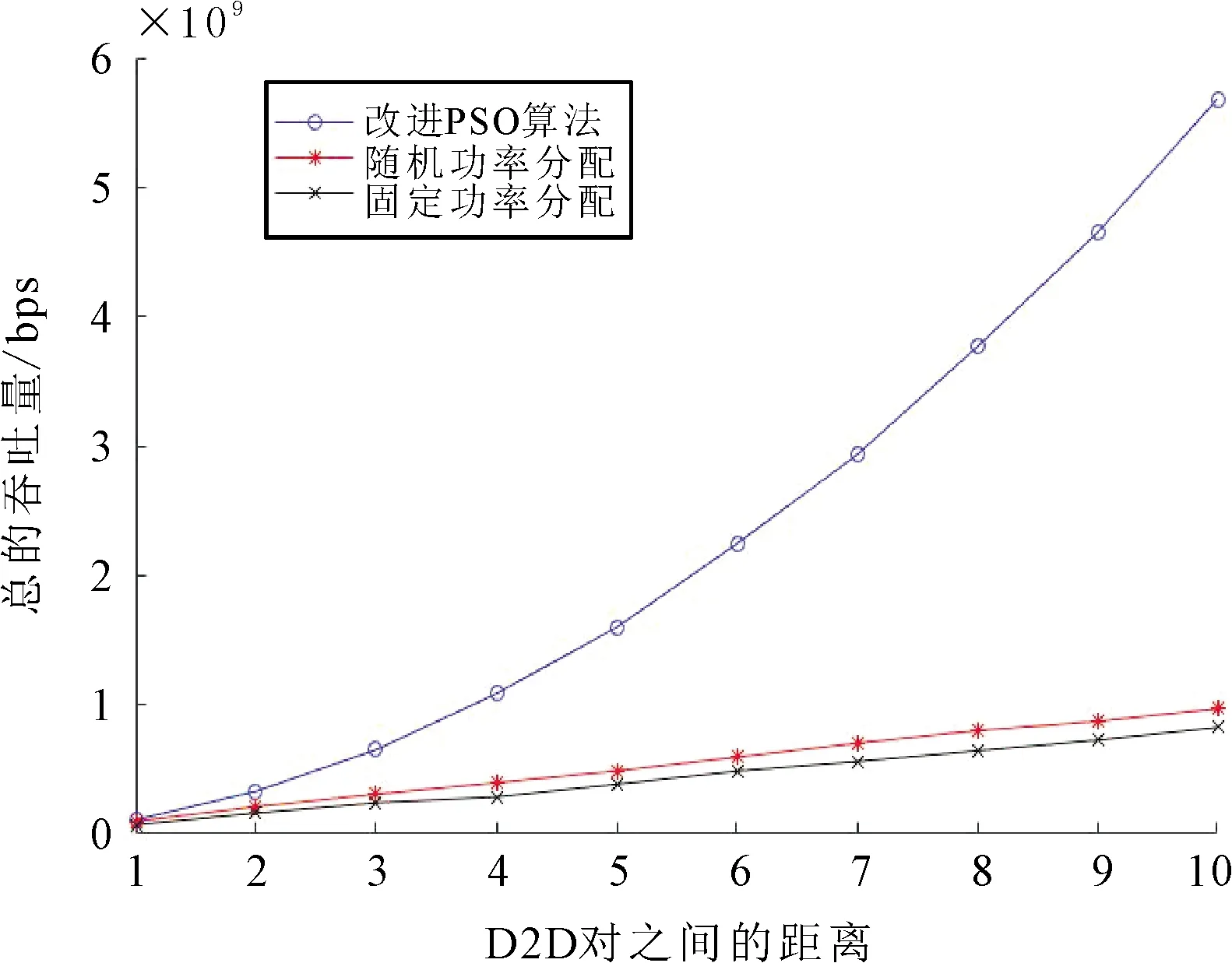
图7 总吞吐量与D2D用户数的关系

图7表示系统总吞吐量与D2D用户数的关系。从图7可以看出，3种算法的吞吐量均随着用户数的增加而递增。随着D2D用户数的增加，蜂窝用户上行链路资源利用率增大，虽然在引入D2D用户后会产生相应的干扰，但整体系统的性能得到了有效的提高。虽然3种算法的吞吐量均随着用户数的增加而增大，但是所提的基于粒子群算法相对其他两种算法的性能提升更加明显，当D2D用户数从第2对开始一直到第10对，其吞吐量明显高于其他两种算法。因此，所提算法能够更加有效的提升系统性能。

图8是不同算法吞吐量与迭代次数的关系。

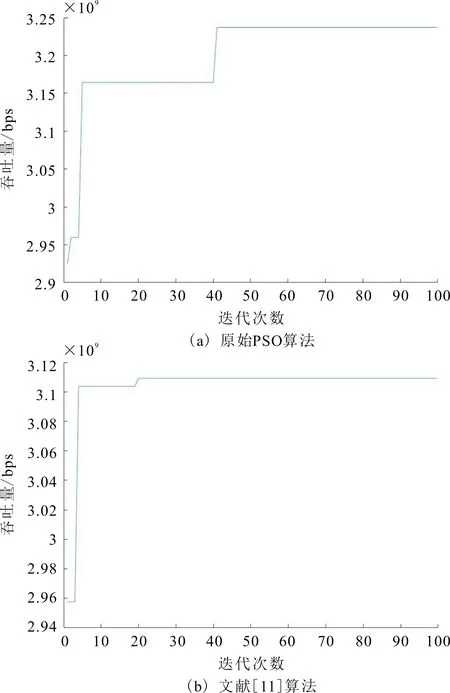
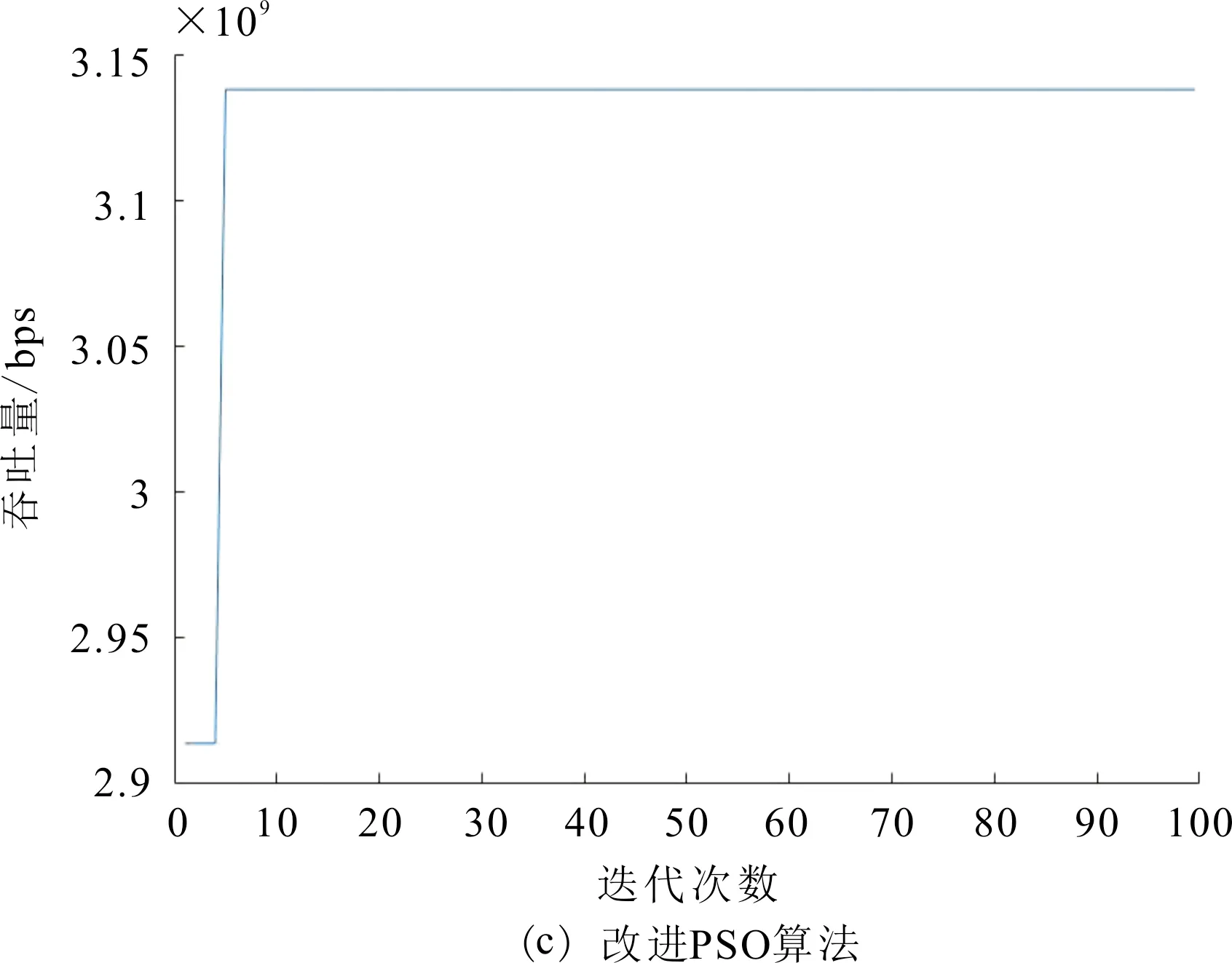
图8 不同算法吞吐量与迭代次数的关系

由图8可以看出，图8(a)和图8(b)分别是原始PSO算法与文献[11]所提算法吞吐量与迭代次数的关系图，从图8(a)中可以看出，原始PSO算法在第41次迭代时吞吐量达到最优，图8(b)中算法在第20次迭代时吞吐量达到最优。图8(c)是改进的PSO算法，改进算法在第5次迭代时吞吐量就达到了最优。因此，所提算法收敛性优于原始算法和文献[11]中算法的收敛性。

4 结语

针对D2D共享蜂窝资源所带来的用户之间的干扰问题，提出基于递减指数函数惯性权重的改进粒子群算法，改进的粒子群算法能够有效解决原始粒子群算法迭代速度慢、寻优能力差等问题。改进的粒子群算法通过多次迭代，给蜂窝用户和D2D用户分配最优的发送功率。仿真结果表明，改进的算法在降低干扰的同时，能够有效地提升系统的整体吞吐量性能。另外，改进后的算法迭代速度明显优于原始粒子群算法和文献[11]中的算法，并且保证了D2D用户和蜂窝用户的通信质量。目前的研究仅仅考虑了单小区场景，在实际情况下，相邻小区之间也存在相互间的干扰，改进的算法可以考虑应用到多小区场景下，集中在D2D用户与蜂窝用户之间的功率分配问题。