基于图像增强技术的钢铁材料微观组织图像识别的研究

于金鑫，李欣健，王翠萍，徐 勇，刘兴军,3

(1.厦门大学 材料学院和福建省材料基因工程重点实验室，厦门 361000；2.哈尔滨工业大学(深圳)计算机科学与技术学院，深圳 518000；3.哈尔滨工业大学(深圳)材料基因与大数据研究院，深圳 518000)

0 引言

近年来，机器学习与数据挖掘技术已经逐渐应用于材料学研究中[1-3]。利用机器学习技术，可以基于材料数据建立描述材料成分-工艺-微观组织-性能间定量关系的数学模型，之后使用模型可以实现高通量的材料性能预测，加速材料设计[4-5]。目前，已经有人使用此方法对压电材料、热电材料、非晶玻璃等功能材料[6-8]进行了设计工作并取得了一定成果。需要注意的是，以上工作在进行材料设计时并没有考虑各个影响因素对材料微观组织的影响。

成分和加工工艺的不同会使材料的微观组织发生明显变化。以钢铁为例，在不同条件下可能形成多种微观组织，如珠光体、铁素体、渗碳体、奥氏体、莱氏体，这给组织的识别提高了难度。此外，在研究种需要对各个组织进行较为精确的分类并对其进行定量分析，采用传统的人工识别可能会需要较多的时间。因此，目前急需寻找新的方法进行微观组织的鉴定工作。

图像识别技术目前已经被广泛应用与各个行业中，如人脸识别、文字识别、图像增强等领域[9]。然而，目前图像识别技术在材料学领域的研究并不多，这是因为图像处理技术往往对数据的数量有较高的要求；以当前流行的深度学习为例，数据的数量级往往在万级、十万级甚至更高，在材料研究中单个实验室想要获得如此多的数据是很困难的。为了弥补数据量的不足，往往需要从文献中提取，然而文献中的图片质量层次不齐，为建立高精度的模型带来难度。

针对以上问题，本文尝试采用图像处理技术对文献中收集到的低分辨率钢铁组织照片进行处理，提高数据质量。再采用多种机器学习算法对其进行数据挖掘，以建立具有高精度的钢铁微观组织识别分类模型，为提升材料设计的进展提供相应基础工作。

1 研究方法

1.1 数据

本文的数据集共包含76张图片，图像的大小不等，最小的只有251×171像素，最大的有800×551像素，数据集的来源主要是通过实验获得，还有一些是通过书籍和论文中摘取。数据集共包含奥氏体组织照片16张、贝氏体9张、莱氏体6张、马氏体16张、铁素体6张、魏氏组织7张、珠光体16张共7个大类，其中马氏体包含了板条状马氏体7张和针状马氏体9张、珠光体包含了片状珠光体7张和粒状珠光体9张。

1.2 图像增强算法及特征提取算法

本文使用的原始图像质量较差，如果直接采用机器学习算法对图片数据集进行数据挖掘难以获得具有高精度的分类模型。因此，本文首先采用图像增强技术提高图像质量，之后采用图像特征提取技术获得最能代表图像信息的特征。

1.2.1 直方图均衡化

直方图均衡化实质上是对图像的灰度直方图进行非线性拉伸，将图像的灰度值r变换为s，使拉伸变换后的灰度直方图在灰度范围内均匀分布，灰度直方图变得平滑化[10]。本文中使用以下的映射函数，将图像的灰度直方图进行直方图均衡化处理。

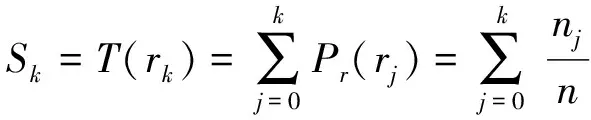
(1)

式中，k=0,1,2,3,…,n-1，rk是第k个灰度级的像素值，Sk是经过直方图均衡化后的第k个灰度级的像素值，Pr(r)是指r的概率密度函数，nj表示灰度级为j的像素的数量，n表示数字图像中像素的总数。

1.2.2 图像去噪

本文采用同态滤波方法进行图像去噪。同态滤波方法既可以去掉图像的乘性噪声，也可以增加对比度以及标准化亮度，达到图像增强的目的[11]。通过使用高频滤波器H(u,v)，可以去除图像的乘性噪声，达到图像增强的目的。本文中使用Gaussian高通滤波器，即:

(2)

式中，D0表示通带的半径，D(u,v)表示到频谱中心的欧氏距离，其计算公式如下：

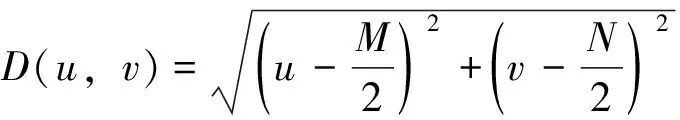
(3)

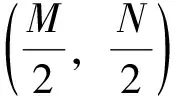
1.2.3 图像线性变换

灰度线性变换被称为图像的点运算，是数字图像处理中容易实现而且效果较好的空间域图像增强技术，其对于像素的运算是基于图像的当前像素以及灰度变换函数[12]。灰度线性变换可以改善图像画质，使图像的显示效果更加清晰。其灰度变换是将图像中所有的像素点按照灰度变化函数进行线性变换，该线性变换函数为：

I(s)=k·I(r)+b

(4)

式中，I(s)表示变换后的图像灰度像素值，I(r)表示变换前的图像，k表示线性变换的斜率，b表示线性变换函数的截距。

1.2.4 图像锐化

在对图像进行了去噪等处理后，图像将平滑化，会出现图像边缘或者图像轮廓模糊的情况。为了减少这类不利效果对图像的影响，需要使用图像的锐化技术，使图像边缘、轮廓以及图像中的细节变得更加清晰[13]。

本文中使用空域滤波法进行图像锐化[14]。空域滤波是基于邻域处理的增强方法，直接在图像所在的二维空间进行处理，即对每一个像素的灰度值进行处理。采用的像素点(i,j)新灰度值的运算方式g(i,j)为：

g(i,j)=|f(i-1,j-1)+f(i-1,j+1)+

f(i,j)+f(i+1,j-1)+f(i+1,j+1)|

(5)

式中，f为对应像素点的原灰度值。

1.2.5 图像特征提取特征

纹理特征是数字图像的全局特征，它能够反映数字图像缓慢变化或者周期性变化的组织排列属性[15]。不同类型钢铁显微组织图像具有区别明显的纹理，因此，使用纹理特征作为图像的分类依据。本文中所使用的纹理特征包括：数字图像的灰度值平均值、灰度值方差、平滑度、三阶矩、一致性、熵、灰度共生矩阵能量的均值与方差、灰度共生矩阵熵的均值与方差、灰度共生矩阵惯性矩的均值与方差、灰度共生矩阵相关性的均值与方差共计14个特征。

1.3 机器学习分类算法

本文中采用目前机器学习的三种主流分类算法：随机森林(Random Forest, RF)、支持向量机(Support Vector Machine, SVM)和集成树(Ensemble Tree, ET)进行建模，采用精度更高的算法建立分类器。本文中所有机器学习分类算法的计算均采用Matlab R2016a完成，采用“RF_Class_C”构建随机森林模型，采用“libsvm”构建支持向量机模型，采用Matlab内嵌的“ensemble”构建集成树模型。

1.3.1 随机森林算法

随机森林算法是集成学习的一种[16]。集成学习[17]的核心思想是为了解决单个模型或者某一组参数的模型所固有的缺陷，将多个模型整合起来，弥补缺陷，避免模型的局限性。随机森林使用的就是集成学习的思想将多个决策树整合起来变成森林最终预测结果。随机森林算法的基础是决策树[18]。运用决策树进行分类的算法称为决策树分类算法[19]，决策树作为一种弱分类器，采取的是单一的分类决策模式，所以存在很多缺点，比如：过度拟合、分类规则复杂、只能得到局部最优解等。为了避免决策树的一系列问题，通过将决策树和集成学习的思想合并，使用多个决策树组合就得到了随机森林算法。本文中选取的决策树数量为500，其他参数保持默认。

1.3.2 支持向量机

支持向量机是一类按监督学习方式对数据进行二元分类的广义线性分类器，核心是将些线性不可分的问题转化为非线性可分，即在特征空间中建立超曲面将正类和负类分开。SVM使用的非线性函数可以将非线性可分问题从原始的特征空间映射至更高维的希尔伯特空间，从而转化为线性可分问题。SVM可以通过核方法进行非线性分类，是常见的核学习方法之一。SVM最常用的核包括线性核、多项式核、径向基函数核、Sigmoid核。本文中选取径向基函数核作为核函数，其他参数保持默认。

1.3.3 集成树

集成树模型也是一种集成学习方法，是基于提升(boosting)思想建立的一种算法。其核心是利用一个基础算法进行预测，然后在后续的其他算法中利用前面算法的结果，重点处理错误数据，从而不断的减少错误率，使用几种简单的弱算法来达到很强大的组合算法。集成树模型是以决策树模型为基础，通过提升把决策树提升为强学习算法的模型。目前常用的提升方法有Adaboost、Gradient Boosting、XGBoost等。本文中选取Adaboost，决策树数量为500，其他参数保持默认。

2 结果与讨论

2.1 图像增强方法对组织分类的影响

本文分别采用线性变换、去噪和锐化增强算法对图片进行图像增强处理。图1是采用不同算法之后的图像与原始图像的对比。可以发现经过图像增强算法处理后，与原图像相比处理过的图像的组织纹路更为清晰，图纸特征更为突出。为了确认各个方法对模型精度的提升程度，对使用不同图像增强算法处理获得后的数据集进行数据挖掘，以选择具有更高精度的方法提取图片特征，进行下一步的图像分类工作。

图1 不同图像增强算法的处理效果

首先采用采用直方图均衡化方法对所有图像进行处理；之后采用不同图像增强策略对原始图像进行质量提升。采用的策略有：①去噪；②去噪+线性变换；③去噪加锐化;④去噪+线性变换+锐化。应用适用性较为广泛的随机森林算法对不同增强策略生成的图像特征进行数据挖掘，建立组织分类器。通过对比不同分类器的精度对各个策略进行评估。

图2是采用不同图像增强策略建立的组织分类器的精度。可以发现，基于原始数据采用随机森林算法建立的组织分类器的精度为84%，而除了采用去噪+锐化的策略之外，其他策略均可以提高模型精度。其中，采用去噪+线性变换+锐化的图像增强策略对模型的精度提高最为显著。

2.2 机器学习算法对组织分类的影响

通过2.1节的讨论，可以发现对图像进行去噪、线性变化和锐化后再提取的特征在建模时具有最高精度。因此在本节中，采用多种机器学习分类算法对此类特征进行数据挖掘，建立组织分类器。

图3为三种分类器的精度对比，由图可见，随机森林的精度是最高的，达到了89.34%，而集成树和支持向量机的精度分别有82.67%与80%。因此，采用精度最高的随机森林算法建立钢铁组织分类器。

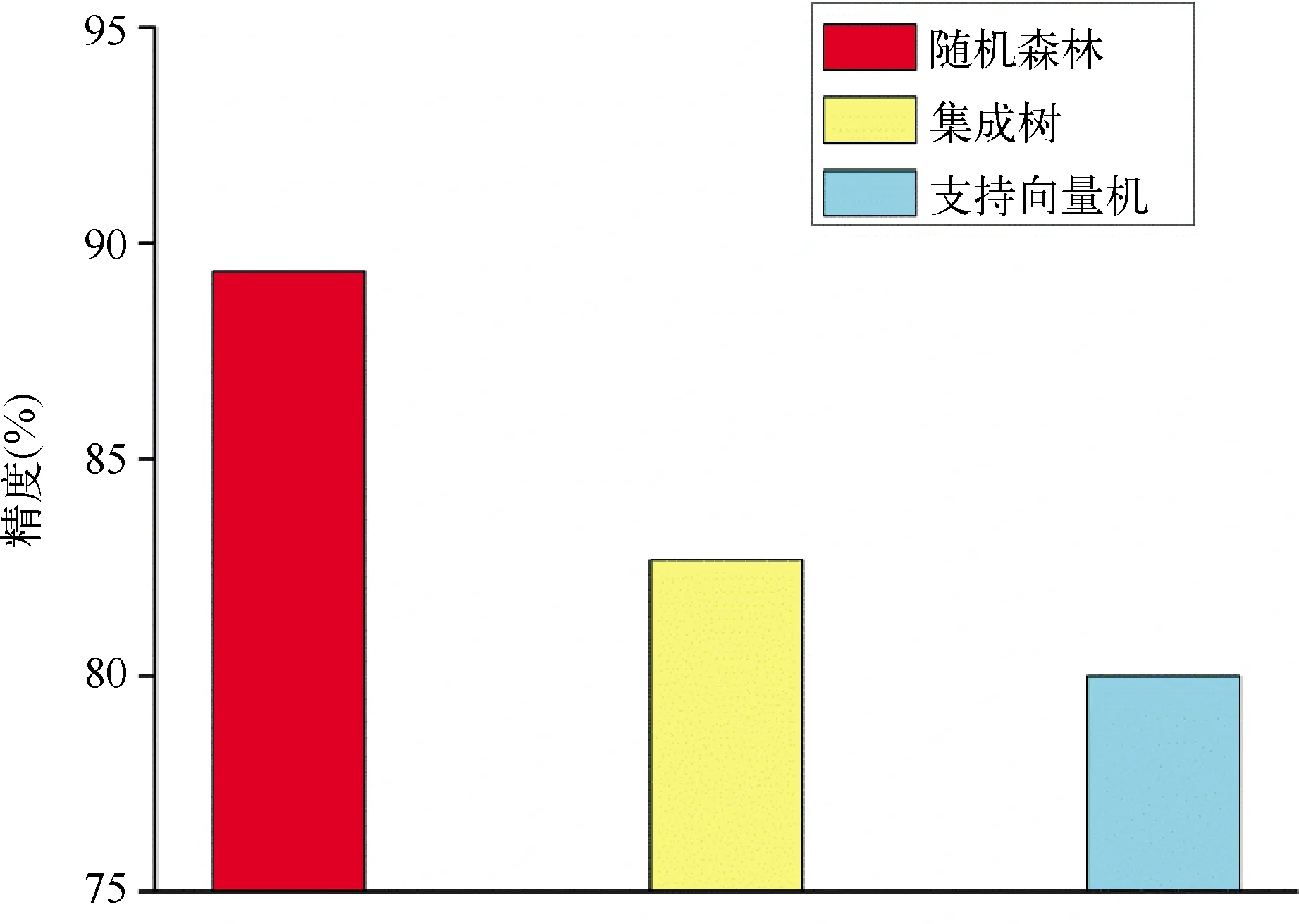
图3 随机森林、集成树和支持向量机的分类效果

2.3 随机森林算法效果分析

为了更好的表示随机森林的分类效果，采用主成分分析方法(PCA)将原始的14维特征压缩至3维。主成分分析方法是一种统计方法，通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。在将14维特征压缩至3维后，重新计算了模型的精度。结果发现精度并没有降低，因此，3维的分类结果可以较好地代表14维的分类结果。

图4为用PCA将特征维度压缩至3维的随机森林分类效果示意图。图中九种颜色代表了九种组织；圆形为模型正确分类数据，星形为错误分类数据。可以发现，组织分类器可以较为准确的进行组织类型的分类判断。图4中大部分同一种类组织数据分布较为集中，如红色的奥氏体数据。这说明此类数据具有较高的特征相似度。然而部分数据的分布比较散乱，如棕色的莱氏体数据。这说明模型目前对此类组织的识别效果不是很理想，这可能是因为目前的数据集中此类数据较少，无法提取更为明显的分类特征造成的。在今后的工作中，通过增加数据样本，可能会改善模型的分类效果。

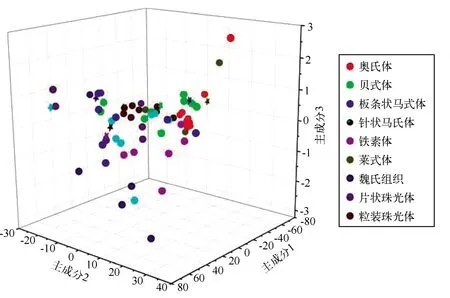
图4 用主成分分析方法将特征维度压缩至3维的随机森林分类效果示意图

3 结论

本文通过使用图像增强技术和模式识别技术，对钢铁的微观组织图片进行了图像处理和建立分类器的工作。通过使用将直方图均衡化、图像去燥、图像线性变化、图像锐化结合的图像增强策略，显著提高了微观组织识别的精度。基于随机森林算法的分类算法的精度最高，使用计算机分类，可以较为快速、准确的识别钢铁组织。此方法有望为材料设计提供有益的指导信息。