磨耗后轮轨型面接触关系及线路适应性分析
2021-06-17杨震寰戴焕云石俊杰
杨震寰,戴焕云,石俊杰,魏 来,干 锋
(1.西南交通大学 牵引动力国家重点实验室,四川 成都 610031;2.中车唐山机车车辆有限公司,河北 唐山 063500)
轮轨关系是影响车辆系统动力学性能的关键因素,随着我国高速铁路网的逐渐扩大,车轮磨耗和钢轨磨耗的情况日趋复杂,不同车辆与不同线路相匹配后轮轨关系会产生明显的变化,掌握具体的轮轨匹配关系是保证动车组安全运行的关键。
国内外学者针对轮轨关系对车辆动力学性能的影响开展了大量研究。罗仁等[1]阐述了我国动车组运营初期产生的线路适应性问题,分析了轮轨匹配关系和一系定位刚度对动力学性能的影响,提出了提高动车组线路适应性的方法。黄照伟等[2]对我国高速铁路车轮磨耗特性进行跟踪测试,通过仿真分析了凹型磨耗和偏磨现象对车辆动力学性能的影响,指出反相偏磨较同向偏磨有利于提高车辆运行稳定性。金学松等[3]对我国动车组轮轨断面横向磨耗进行了研究,分析了踏面凹型磨耗对车辆动力学性能的影响,研究了钢轨侧磨的形成原因,提出了相应的改进措施。马晓川等[4]研究了LMA型磨耗后踏面与60钢轨、60 N钢轨匹配时的直线与曲线动力学性能,对2种钢轨抵抗磨耗及滚动接触疲劳的能力进行了分析。Polach[5]提出了基于3 mm等效锥度和一种新的非线性参数共同评估轮轨关系的方法。文中指出只用3 mm等效锥度评估轮轨关系的局限性,说明新加入的参数可以很好地解释在相同等效锥度下出现的不同临界速度及不同的Hopf分岔图亚临界特性等动力学现象。孙宇等[6]使用一种改进的Kik-piotrowski方法研究模拟凹型磨耗车轮与钢轨的非Hertz接触和多点接触行为,文章指出凹型磨耗下,车轮静态接触点和动态接触点分布于2个孤立的区域,车轮磨耗会使得轮轨中高频垂向力略有增大,并会显著增大轮轨横向力。以上文献从各个角度详细阐述了轮轨关系对车辆动力学性能的影响,取得了丰硕成果,但对磨耗后轮轨型面匹配的特性分析较少。Wei等[7]通过线路试验得到动车组抖车时车体模态频率和转向架蛇行频率,结合实测轮轨廓形和刚柔耦合动力学模型再现了抖车现象,文章指出磨耗后的轮轨匹配呈现出较大的等效锥度,进而导致转向架失稳并激发车体菱形模态,使得车体产生异常抖动。Qi等[8]结合实测轮轨型面和动力学试验数据,指出轮轨关系的变化是动车组在不同线路运行时动力学性能不同的根本原因,可通过车轮镟修,增大抗蛇行减振器的刚度,增大一系纵向定位刚度来解决这种问题。Wilson等[9]基于实测线路轮轨匹配关系,并结合车辆的悬挂参数解释了重载列车在线路上出现失稳现象的原因。以上文献结合了实测轮轨数据阐述了轮轨关系对车辆动力学性能的影响,但对轮轨接触关系变化的具体原因阐述较少。
轮轨接触几何关系的计算方法日趋完善,如任尊松[10]结合轮轨间距离函数和轮轨间弹性压缩量提出了一种轮轨间多接触点判定的计算方法,并使用LMA踏面进行了验证。干锋等[11-12]基于轮轨刚性接触给出了轮轨准弹性接触的计算方法,开发了用于计算磨耗后车轮踏面轮轨接触关系的TPLWRSim软件,比较了不同算法的优越性,指出谐波法和UIC 519[13]方法能更准确地计算等效锥度。
钢轨打磨的研究也有所进展。任娟娟等[14]选取武广高速铁路实际打磨后的钢轨廓形,建立“车轮-钢轨”有限元模型进行计算,计算结果表明钢轨打磨使得接触斑形状更加规则,使接触点位置向轨顶中心移动,可有效减少钢轨病害。毛鑫等[15]提出了一种基于轮径差函数的曲线钢轨打磨方法,该方法可通过合理设计轮径差曲线和接触位置分布有效用于重载和高速铁路的钢轨打磨。
本文针对现场测试中发现的动车组跨线运行异常振动问题,从轮轨接触关系角度开展研究。首先对实测的不同车辆踏面磨耗和不同线路钢轨廓形做详细阐述,进一步对具体车辆和线路匹配的轮轨关系进行详细分析,最后结合踏面磨耗和轨道廓形差异深入探究导致轮轨关系差异的具体原因,旨在为研究动车组跨线运行时的轮轨接触关系提供参考。
1 研究背景
在我国时速250 km动车组的运行过程中,曾出现常B线路的动车组在跨线运行到A线路时构架端部横向加速度显著增大的现象,但经常运行于A线路的动车组在镟修末期仍能保持良好的动力学性能。取常在B线路运行的动车组构架端部横向加速度线路测试数据进行0.5~10 Hz带通滤波,见图1。该动车组运行于A线路时构架横向加速度频谱图见图2。
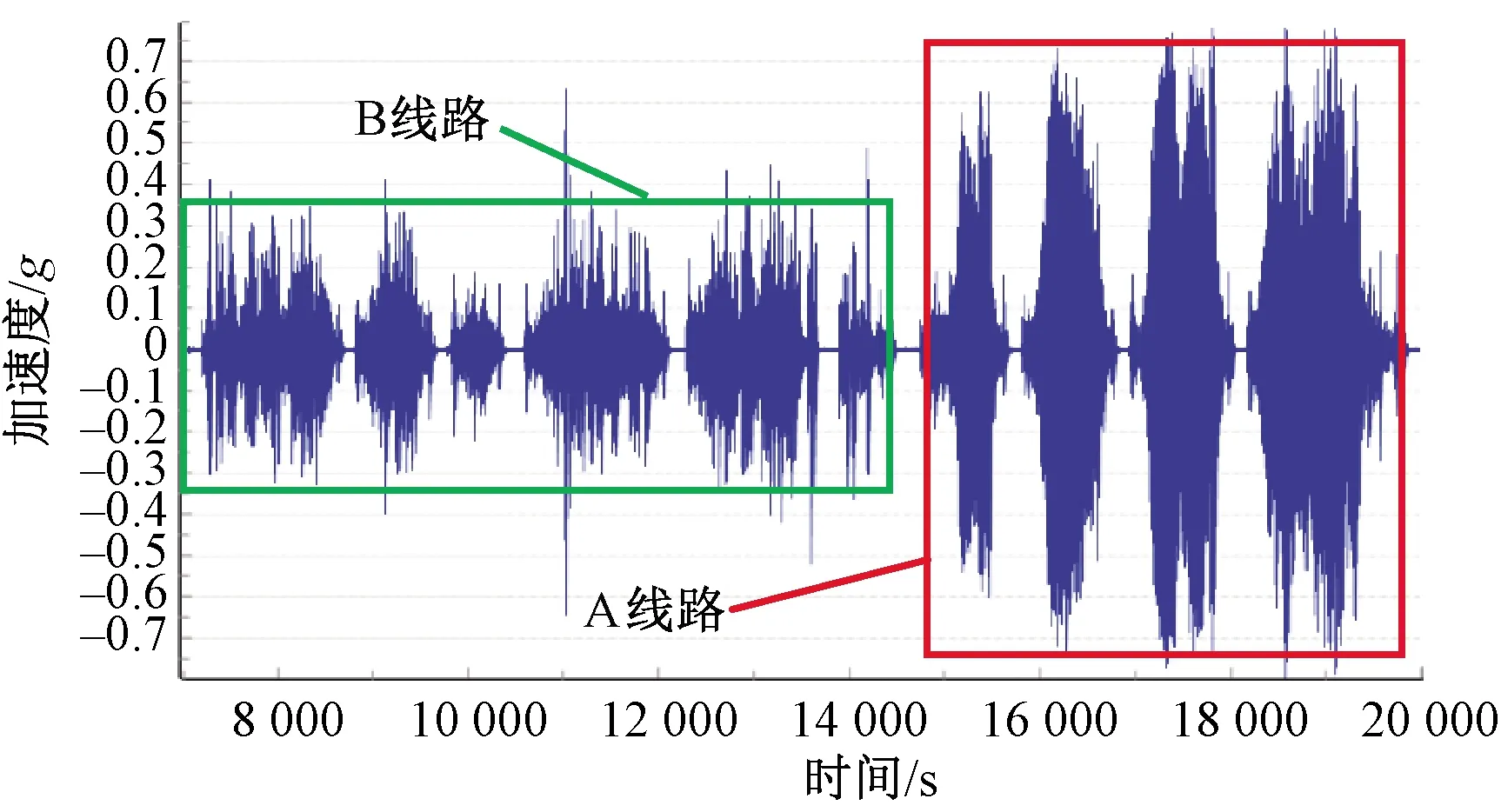
图1 实测动车组构架横向加速度(带通滤波0.5~10 Hz)
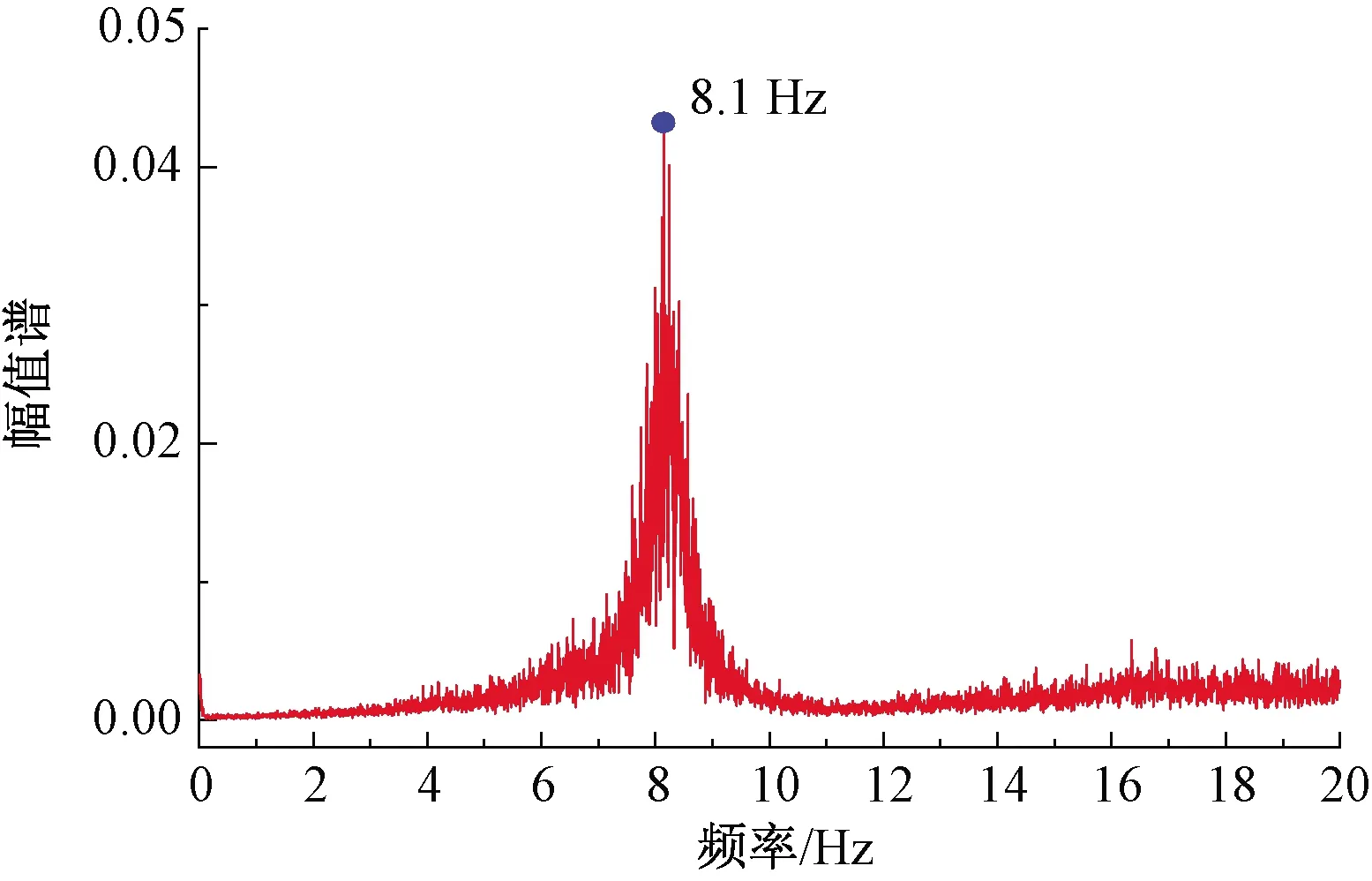
图2 动车组运行于A线路时构架横向加速度频谱
由图1可知,在B线路运行时构架横向加速度基本在0.2g以内(g取9.81 m/s2),在A线路出现了明显的谐波振动,且幅值大于0.4g。
由图2可知,该动车组在A线路上部分区间构架横向加速度谐波主频为8.1 Hz,可初步判定其已经发生了大等效锥度下的转向架蛇行运动,即二次蛇行运动。虽然构架横向加速度小于报警限值(0.8g),但该频率的谐波振动会通过悬挂系统传递到车体,易与车体一阶菱形振动模态耦合,产生共振,引起车体剧烈振动,极大降低动车组运行平稳性和旅客乘坐舒适度。
影响动车组蛇行运动稳定性最关键的因素就是轮轨关系。因此,本文对2条线路的实际轮轨关系进行分析,深入探究引起动车组蛇行运动的根本原因。
2 钢轨廓形和车轮踏面测试
分别取2组经常运行于A线路的动车组(以下简称“A车”)和经常运行于B线路的动车组(以下简称“B车”),在车轮镟修末期使用MINIProf踏面测量仪进行踏面廓形测试。使用Optimess轨面测量仪对A线路钢轨(以下简称“A轨”)和B线路钢轨(以下简称“B轨”)的钢轨廓形进行测试,获得真实的车轮踏面和钢轨廓形。
2.1 A线路钢轨廓形与踏面廓形测试结果
2组A车左轮踏面和5组A线路左轨廓形测试结果见图3。由图3可知,A车左轮踏面出现了与A线路左轨共形的凹型磨耗;左轨轨顶位置较标准廓形靠内侧约0.7 mm,轨顶处廓形与标准廓形接近;左右两侧轨头圆角处均略高于标准廓形,右轨头圆角处圆弧半径大于标准廓形。

图3 A线路左轨廓形与车辆左轮踏面廓形
2组A车右轮踏面和5组A线路右轨廓形测试结果见图4。由图4可知,A车右轮踏面仍存在与A线路右轨共形的凹型磨耗;右轨轨顶位置较标准廓形靠内侧约1 mm,左轨头圆角廓形与标准钢轨廓形接近,图示横坐标85~95 mm处略低于标准廓形,其右轨头圆角圆弧半径仍然大于标准廓形。

图4 A线路右轨廓形与车辆右轮踏面廓形
A车左右侧车轮的踏面磨耗量见图5。由图5可知,各车轮最大磨耗位置均位于踏面名义滚动圆处,2组动车组左轮踏面最大磨耗量分别为1.47 mm和1.38 mm;2组右轮踏面最大磨耗量分别为1.5 mm和1.58 mm。

图5 2组A车轮对踏面磨耗量
2.2 B线路钢轨廓形与踏面廓形测试结果
2组B车左轮踏面和5组B线路左轨廓形测试结果见图6,图中2组踏面廓形在轮缘处存在差异是车轮镟修造成的。由图6可知,B车左轮踏面也出现了与B线路左轨共形的凹型磨耗;B线路左轨轨顶位置与标准廓形接近,左侧轨头圆角较标准廓形低,图中横坐标85~95 mm范围内也低于标准廓形,整个轨头显得较尖。
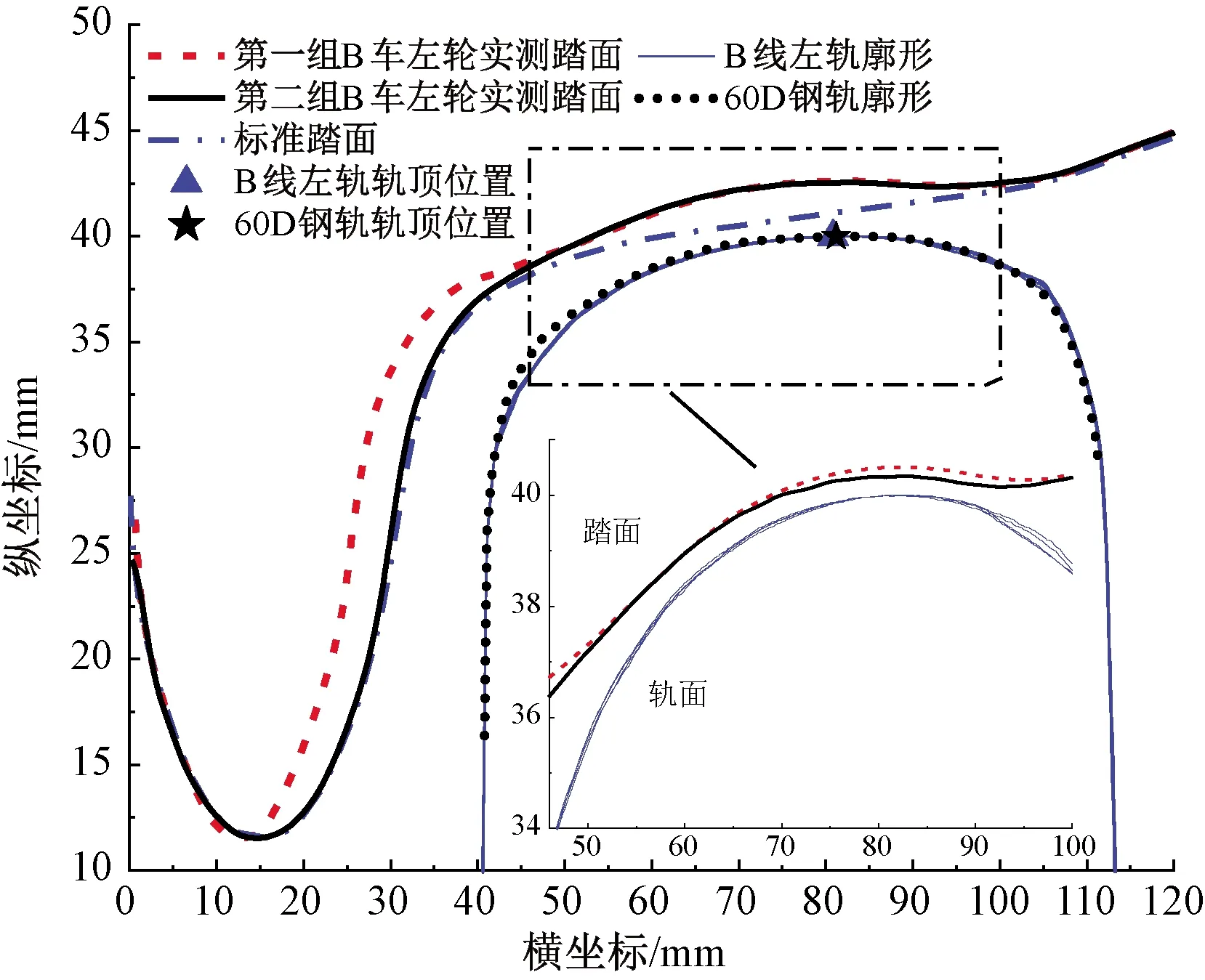
图6 B线路左轨廓形与车辆左轮踏面廓形
2组B车右轮踏面和5组B线路右轨廓形测试结果见图7。由图7可知,B车右轮踏面仍然存在与B线路右轨共形的凹型磨耗;B线右轨轨顶位置较标准廓形靠外侧约1.5 mm;左轨头圆角处较标准廓形低,右轨头圆角处圆弧半径较标准廓形大,轨头显得较尖。
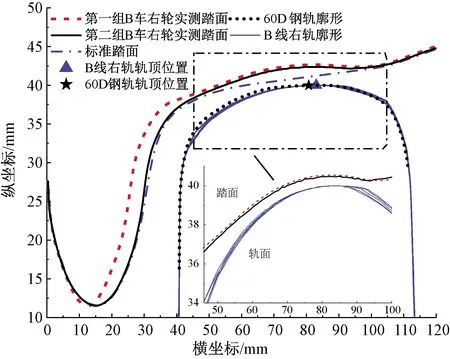
图7 B线路右轨廓形与车辆右轮踏面廓形
2组B车轮对踏面磨耗量见图8。由图8可知,B车左轮最大磨耗位置略靠向名义滚动圆外侧,2组左轮踏面最大磨耗量分别为1.71、1.72 mm,左轮磨耗量曲线斜率的绝对值较大,这与左轨较尖的廓形有一定关联。2组右轮最大磨耗位置位于滚动圆外侧3~5 mm处,这与右轨轨顶位置靠外侧有直接的关联;2组右轮踏面最大磨耗量分别为1.7、1.45 mm。
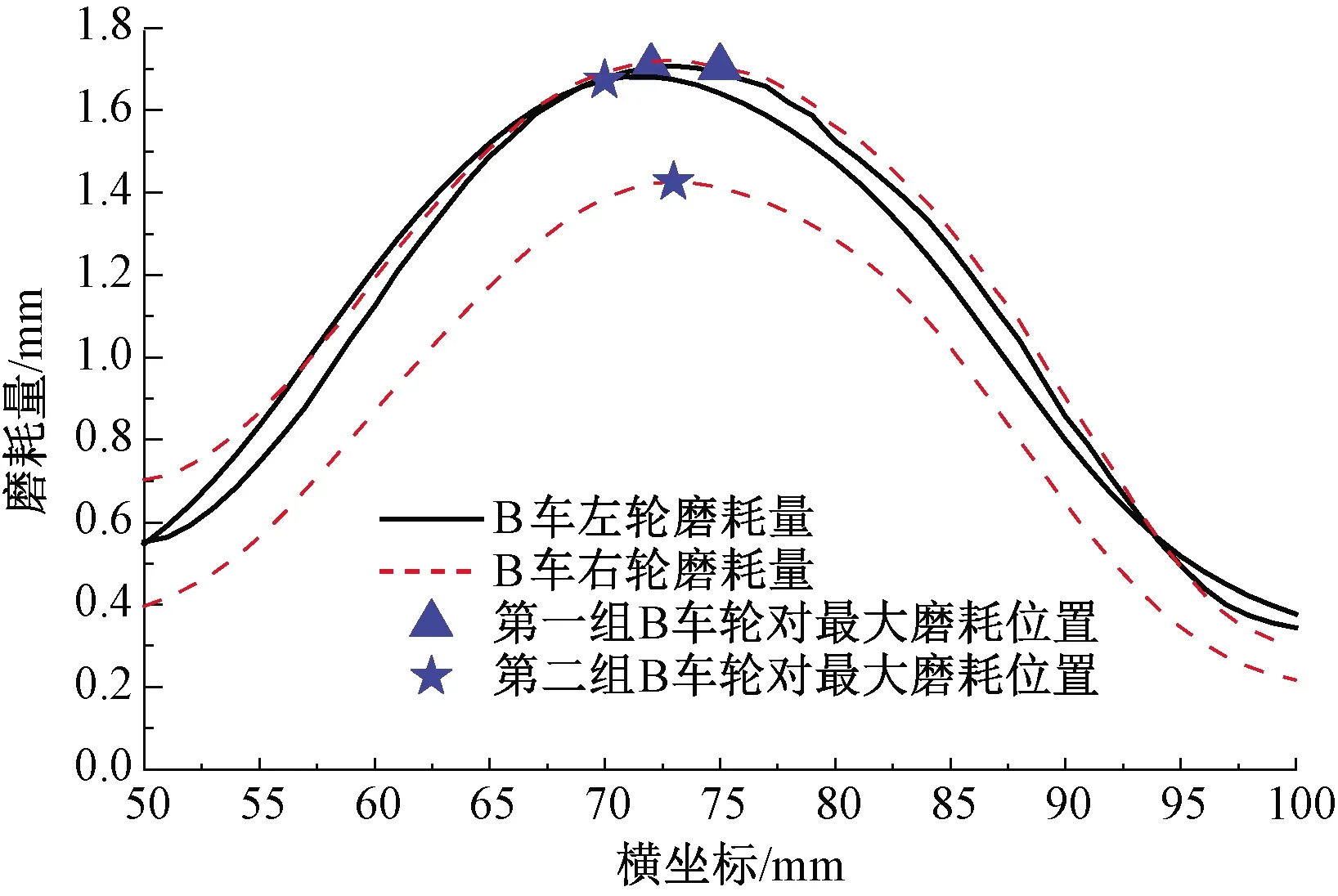
图8 2组B车轮对踏面磨耗量
3 实际轮轨接触关系
取上述实测钢轨廓形和车轮踏面,计算UIC 519[13]等效锥度、接触带宽,并计算实际轮轨匹配的接触点位置,从而具体地展现动车组在实际运行中的轮轨关系。
3.1 等效锥度
3.1.1 UIC 519[13]等效锥度计算方法
由UIC 519[13]标准,设轮对纵向运动速度为v,轮对横移量为y,名义滚动圆半径为r0,左右轮实际接触滚动圆半径差为Δr,接触点跨距为a,则由轮对接触几何关系[16]和轮对在轨道上的横向运动微分方程可得
(1)
式(1)为二阶常系数线性齐次微分方程,其解形式为正弦函数,波长L可表达为
(2)
式中:γ为锥形的角度,本式即为Klingel公式。
实际的车轮踏面并不是锥形,可采用线性化法,使用等效锥度tanγe代替tanγ,代入(1)式进行线性化计算,方程的初始条件为
(3)
给定初值y0后对式(1)进行积分运算,得轮对以幅值为2y的波峰波谷的周期性运动,其波长为L0,则可使用Klingel公式计算等效锥度
(4)
得到一个等效锥度计算结果后,重新取y0,再对式(1)进行线性化计算,重复上述步骤,即可得到等效锥度随轮对横移量变化的曲线。
3.1.2 UIC 519[13]等效锥度计算结果
为了获得不同线路上轮轨等效锥度的规律,取大量轮对和轨道廓形进行计算。取测试的四列八编动车组每辆车的其中1条轮对,共计32条轮对,分别与一组A线路钢轨廓形和一组B线路钢轨廓形匹配,计算实测轮轨接触关系下UIC 519等效锥度,计算结果见图9(a)。再取图5展示的4条轮对,各匹配前文展示的5组A线路钢轨廓形和5组B线路钢轨廓形,计算UIC 519等效锥度,结果见图9(b)。

图9 等效锥度对比
由图9可知,各轮对与A线路钢轨匹配时,其3 mm处等效锥度非常接近,数值在0.35左右;但在0~3 mm范围内等效锥度差异较大,A线路车辆的等效锥度明显小于B线路车辆。轮对横移量由3 mm逐渐减少时,A线路车辆的等效锥度曲线呈现下降趋势,而B线路车辆的等效锥度曲线呈现出急剧增大的趋势。
与A线路相比,各轮对与B线路匹配下的等效锥度明显降低,而A车与B车之间等效锥度幅值相当,均处于较低的等效锥度水平。
3.1.3 锥度增大与车辆蛇行失稳的关系
通过建立车辆系统动力学模型,考虑实测轮轨匹配关系,再现B车匹配A轨时出现的蛇行失稳现象,并验证仿真模型的有效性。通过对比A车和B车分别与A轨匹配时的轮轨关系和极限环幅值,分析锥度增大与车辆蛇行失稳的关系。
实测和仿真得到的构架横向加速度时域波形和频谱图见图10,B车实测踏面与A线路钢轨廓形匹配下构架横向加速度达到0.5g(0.5~10 Hz滤波),主频为8.1 Hz;而仿真得到的构架横向加速度幅值和主频与实测数据较为吻合,能够再现B车与A轨高锥度轮轨匹配造成的车辆蛇行失稳现象,初步验证本文采用的车辆动力学模型是准确的。

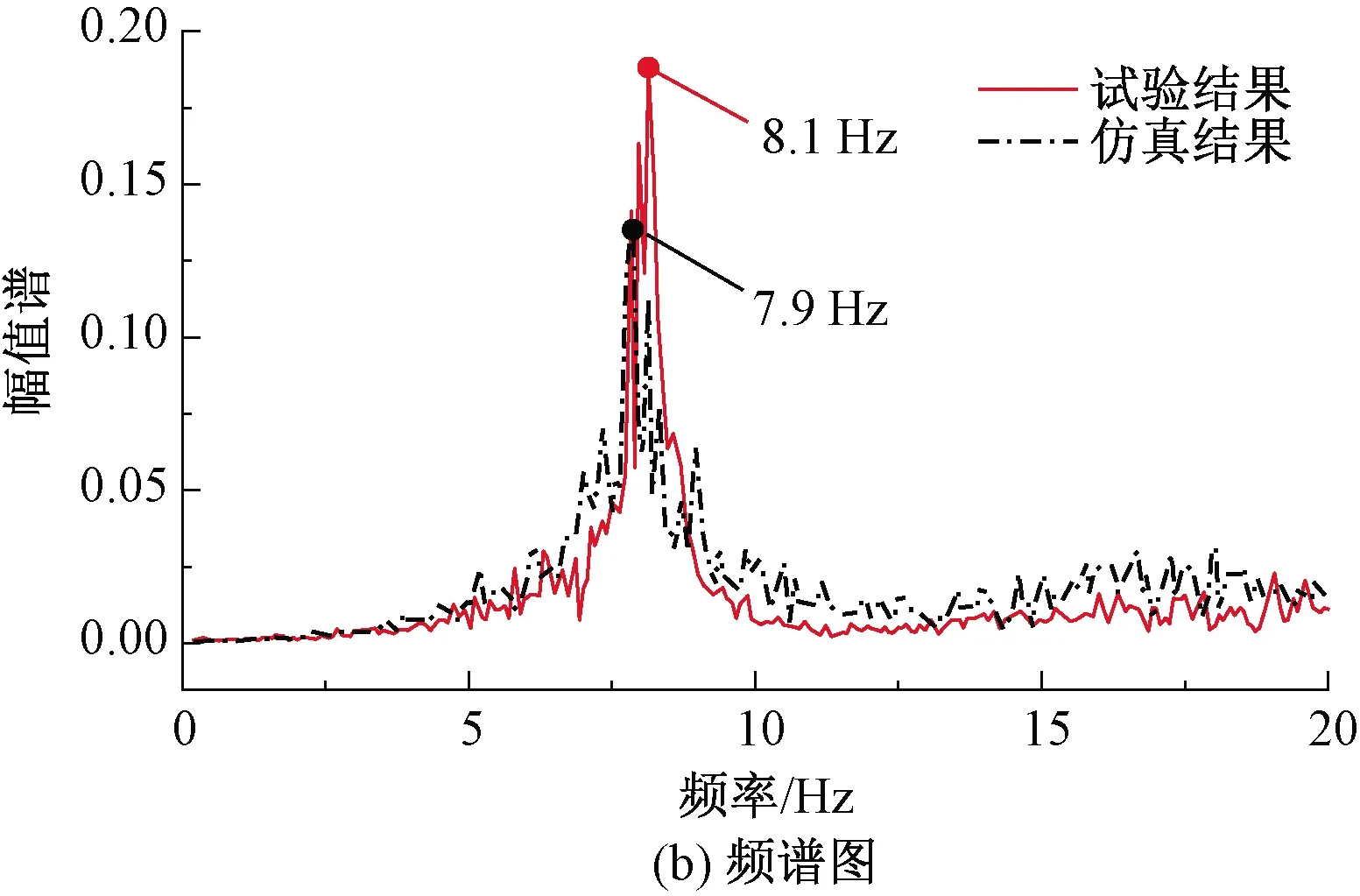
图10 构架横向加速度时域波形和频谱图
图11(a)为A车、B车与A轨匹配时,轮对横向位移在初始激扰下逐渐发展为稳态运动的过程。可见,A车轮对在撤去激扰后能够快速收敛;而B车轮对出现了幅值为1.8 mm的极限环运动,蛇行频率为8 Hz。

图11 轮对蛇行失稳仿真对比分析
图11(b)为仿真计算中使用的不同轮对与A轨匹配后等效锥度计算结果。通过图9和图11(b)给出的轮轨等效锥度曲线可知,与A轨匹配时,A车与B车在0~3 mm横移范围内等效锥度差异较大,B车等效锥度水平极高;而A车锥度水平相对较低。由此可知B车与A轨匹配后0~3 mm范围内等效锥度水平较大是造成B车出现蛇行失稳的原因。
3.2 接触带宽
接触带宽LW指的是[17]轮对在某一横移量下正负方向移动时单侧车轮踏面接触点横坐标的变化范围。计算式可表达为
LW=Py-P-y
(5)
式中:Py、P-y分别为轮对横移量为y、-y时接触点在踏面坐标系中的横坐标。由图9可知,各轮对与不同线路钢轨匹配后在轮对横移量为1.5 mm处等效锥度差异较大,可着重对此处的接触带宽进行分析。
各轮对与不同线路钢轨匹配后轮对横移量为±1.5 mm的接触带宽,结果见图12。由图12可知,各车辆在A线路上运行时,其轮对接触带宽均大于在B线路上运行时的接触带宽。B车左轮在A轨上接触带宽大于A车左轮接触带宽,B车右轮在A轨上接触带宽略小于A车右轮接触带宽。B车匹配A轨时左轮接触带宽比其右轮接触带宽大15~20 mm,A车匹配A轨时左右轮接触带宽较为接近。

图12 轮对横移量为1.5 mm接触带宽对比
B车在B轨上左轮接触带宽略大于A车左轮,右轮接触带宽大于A车右轮。B车配B轨时左轮接触带宽略小于右轮,A车配B轨时左右轮接触带宽差异不大。
3.3 接触点位置
2组A车踏面和2组B车踏面分别与2条线路中各一组钢轨廓形进行匹配,得到接触点位置图,见表1和图13、图14。

表1 各轮对与A轨匹配初始接触点位置 mm

图13 各车辆运行于A线路时轮轨接触点位置对比(单位:mm)

图14 各车辆运行于B线路时轮轨接触点位置对比(单位:mm)
由图13(a)、13(b)和表1可看出,A车与A轨匹配轮对横移量为-3~3 mm时,左轮因为存在凹型磨耗而使得左轮在名义滚动圆附近接触线比较稀疏;右轮在名义滚动圆附近仍然能够产生良好的接触关系。左右轮初始接触点位置差异不大。
B车和A轨匹配轮对横移量为-3~3 mm时,B车左轮由于存在凹型磨耗,未能在踏面名义滚动圆附近产生密集接触线,而是在踏面横坐标55~60 mm范围和85~90 mm范围内与左轨相接触,出现了2个比较孤立的接触区域,见图13(c)、13(d)。同时,B车右轮初始接触点向轮缘一侧靠近,在横坐标55~65 mm靠近踏面内侧范围内产生明显的接触线,使得左右轮初始接触点位置差异较大。
由图14可看出,轮对横移量为-3~3 mm时,B车与B轨匹配后踏面名义滚动圆区域和轨顶区域能够形成良好的接触关系;A车各车轮均能在B轨轨顶产生接触。各轮对与B轨匹配初始接触位置见表2。由表2可知,各轮对右轮初始接触点较左轮靠外侧。

表2 各轮对与B轨匹配初始接触点位置 mm
4 轮轨接触关系差异原因分析
不同车辆与不同线路之间匹配时接触关系会发生变化,等效锥度也有着明显区别,这与踏面和钢轨廓形存在差异有直接的关联。本节将深入分析不同线路轮轨廓形差异,从等效锥度的角度深入分析引起轮轨接触关系差异的原因。
4.1 不同车辆与A线路匹配等效锥度差异分析
A车与B车在匹配A轨时,1.5 mm等效锥度和接触点位置差异非常明显,由图12和图13可知,B车与A轨匹配时,左轮1.5 mm接触带宽较大,右轮1.5 mm接触带宽较小,左右轮初始接触点位置差异较大,这就会造成轮对横移量为1.5 mm时轮径差较大,使得1.5 mm等效锥度增加。而A车与A轨匹配时,左右轮接触带宽差异不大,初始接触点差异不明显,等效锥度不会显著增大。
由此可见,等效锥度的差异是由初始接触点位置和接触带宽的差异造成的。而初始接触点位置和接触带宽的差异就需要从踏面差异的角度进行分析。
将A车与B车左轮踏面进行对比,见图15。B车左轮踏面因与B线路左轨存在共形磨耗,在横坐标60~75 mm和85~90 mm范围踏面廓形曲线斜率的绝对值较A车大,A车左轮踏面较B车平缓。

图15 A车与B车左轮踏面对比
B车左轮与A线路左轨匹配轮对横移量为0的接触关系示意图见图16。由图16可以看出,B车左轮踏面与A线路左轨不共形,踏面名义滚动圆处磨耗深度大,未能与轨顶产生接触;踏面在60~70 mm和85~90 mm处斜率绝对值较大,而A线路左轨左轨头圆角较高,且轨顶平缓,易于产生2点接触,使得初始接触点向外侧移动,并造成接触带宽的增大。

图16 B车左轮与A线路左轨接触示意图
将A车右轮与B车右轮踏面进行对比,见图17。由图17可知,在60~80 mm和85~90 mm范围内,B车右轮踏面曲线斜率绝对值较A车大,再结合图8可知,B车右轮最大磨耗位置较A车偏向外侧。

图17 A车与B车右轮踏面对比
B车右轮与A线路右轨轮对横移量为0时的接触关系,见图18。由图18可知,B车右轮与A线路右轨不共形,踏面名义滚动圆处磨耗深度大,未能与较平缓的轨顶产生接触。85~90 mm范围内踏面斜率虽大,但钢轨右轨头圆角处廓形略低,也未能产生接触;60~70 mm范围内踏面斜率大,能与较高的左轨头圆角产生接触,则初始接触点向轮缘一侧移动,1.5 mm接触带宽也随之降低。

图18 B车右轮与A线路右轨接触示意图
由图3和图4可知,A车轮对与A轨产生了共形磨耗,由图13(a)、13(b)知其左右轮均能在滚动圆附近与较平缓的轨顶产生接触,从而使得左右轮1.5 mm接触带宽和初始接触点位置差异不大。
综上可知,B车轮对在左轮踏面60~70 mm和85~90 mm范围内及右轮踏面60~70 mm范围内斜率绝对值高于A车踏面,造成了A车与B车在与A轨匹配时车轮初始接触点位置和接触带宽出现差异,进一步引起了等效锥度的差异。
4.2 不同车辆与B线路匹配等效锥度差异分析
由图9可知,A车与B轨匹配时,其等效锥度略低于B车与B轨匹配。由表2可知,各轮对与B轨匹配时,各左轮间与各右轮间初始接触点位置差异较小。由图12可知,各左轮间1.5 mm接触带宽较为接近,A车右轮1.5 mm接触带宽小于B车右轮。这就使得A车轮对横移量为1.5 mm时其轮径差略小于B车,则其等效锥度值会略小于B车。
由图14可知,B车右轮能在踏面70~80 mm范围与B轨产生接触,A车在此范围内没有能够产生明显的接触。A车右轮与B线路右轨接触示意图见图19。由图19可知,A车踏面在70~80 mm范围内踏面较平缓,而B线路右轨左轨头圆角较低,两者未能在该范围产生接触。B车右轮70~80 mm处踏面斜率大,仍能在左轨头圆角处产生接触,使得其接触带宽较A车右轮大,从而使得B车轮对等效锥度略大。
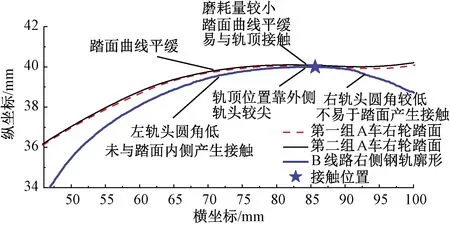
图19 A车右轮与B线路右轨接触示意图
综上,A车右轮踏面70~80 mm范围内斜率绝对值较B车踏面小,使得A车与B车在与B轨匹配时右轮接触带宽出现差异,进一步造成了两者等效锥度出现差异。
4.3 车辆跨线运行时等效锥度差异分析
B车在A线路上跨线运行时等效锥度数值会明显增大,1.5 mm等效锥度差异非常明显,这就说明2条线路钢轨廓形存在差异。本节将对2条线路钢轨廓形进行对比分析,揭示车辆在跨线运行时1.5 mm等效锥度出现差异的原因。
五组A轨与B轨廓形对比见图20,由图20可知,2条线路左轨之间的差异在于A轨在轨道横坐标-25~-5 mm左轨头圆角处高于B轨,在15~25 mm右轨头圆角处也略高于B轨,A轨轨顶较为平缓,B轨轨头较尖;右轨的差异主要在于A轨-25~0 mm左轨头圆角处明显高于B轨,B轨轨顶位置较A轨靠外侧约2~3 mm,且轨头较尖。
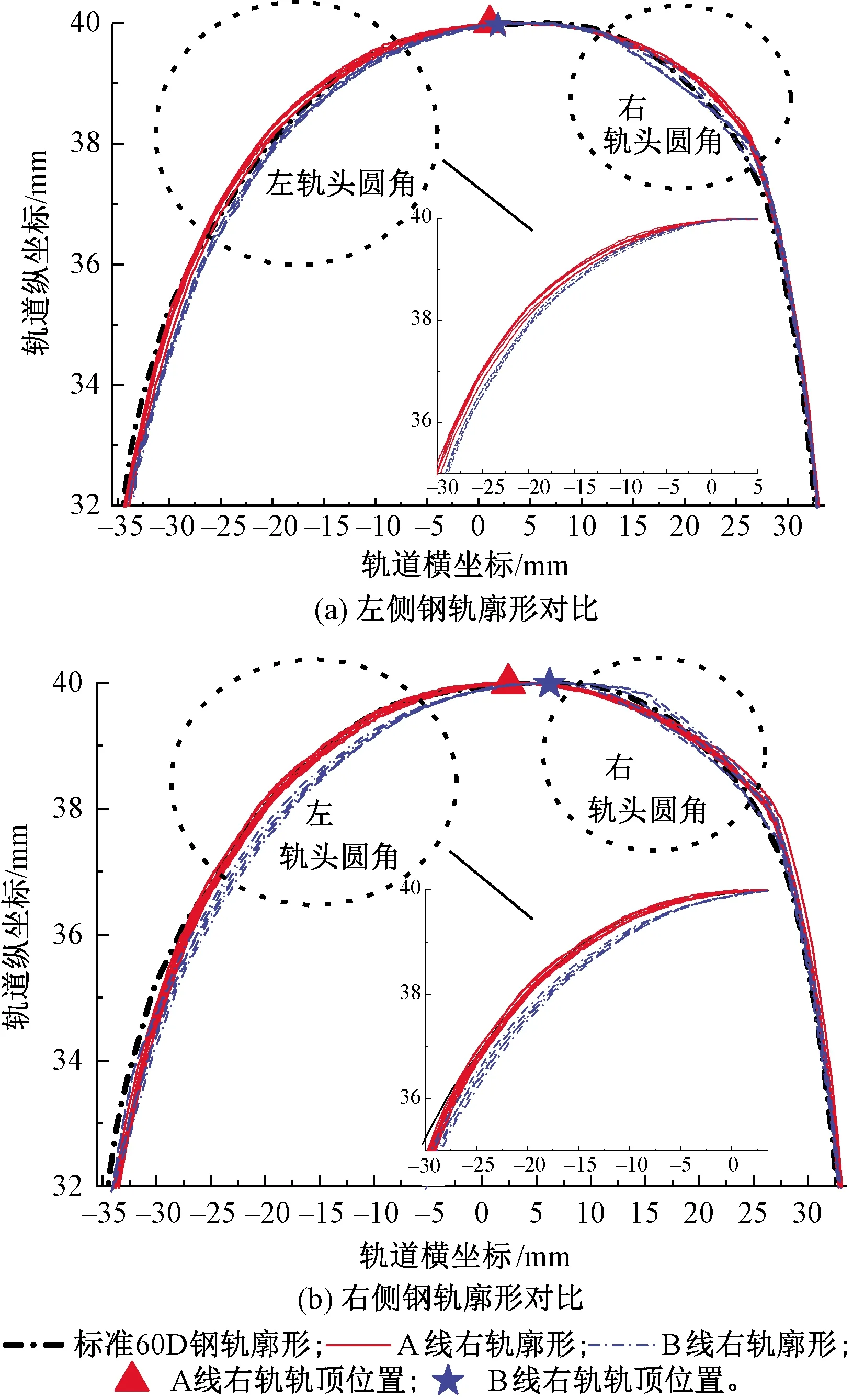
图20 实测钢轨廓形对比
2条线路左轨左轨头圆角高度的差异会使得B车左轮在A线路左轨头圆角和轨顶附近产生2点接触,增大其接触带宽,改变其初始接触点位置;右轨左轨头圆角高度和轨顶位置的差异会使得右轮与A线路右轨匹配时初始接触点向轮缘一侧靠近,与左轮初始接触点位置差异较大,且降低其接触带宽,从而造成B车在A轨上等效锥度的增大。
此外,B线路左右轨道左轨头圆角的差异会使A车左右轮与B线路匹配时初始接触点均向外侧移动,左右轮初始接触点位置差异不大。B线路轨头较尖使得A车轮对在B轨上的接触带宽较小,从而使得A车在B线路上运行时等效锥度较在A线路上运行时小。
2条线路右轨的左轨头圆角和轨顶位置均存在差异,可通过将A线路右轨向外侧移动的办法来消除差异,见图21,移动后A线路右轨在-15~10 mm范围内钢轨廓形会与B线路右轨相近。
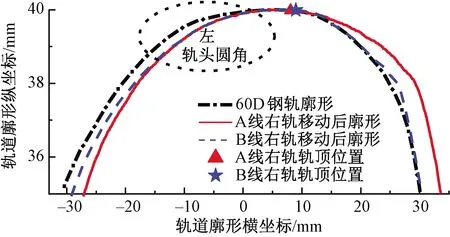
图21 A线路右轨向外侧移动3 mm后廓形图
一组B车轮对与右轨向外移动后的A线路匹配时的等效锥度见图22。由图22可知,当右轨向外侧移动2~3 mm后,B车轮对等效锥度的变化非常明显,0~3 mm等效锥度值明显降低,等效锥度曲线形状与B车与B轨匹配等效锥度曲线相似。B车轮对与右轨移动3 mm后的A轨匹配接触点位置见图23。由图23可知,此时由于左轨头圆角的降低和轨顶的移动,右轮的接触点位置向外侧移动,右轮接触线与B车匹配B轨时接触线相似。

图22 B车轮对与右轨移动后的A轨匹配等效锥度

图23 B车轮对与右轨移动3 mm后的A轨匹配接触点位置(单位:mm)
A车轮对与右轨移动后的A轨匹配等效锥度见图24。由图24可知,A线路右轨移动后,A车与A轨匹配等效锥度值有所降低,且与A车匹配B轨时等效锥度曲线接近。A车轮对与右轨向外移动3 mm后的A轨匹配接触点位置见图25。由图25可知,其轮轨初始接触点向外侧移动,接触点位置与图14(a)、14(b)中A车与B轨匹配时相似。
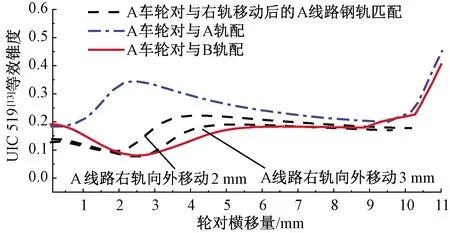
图24 A车轮对与右轨移动后的A轨匹配等效锥度
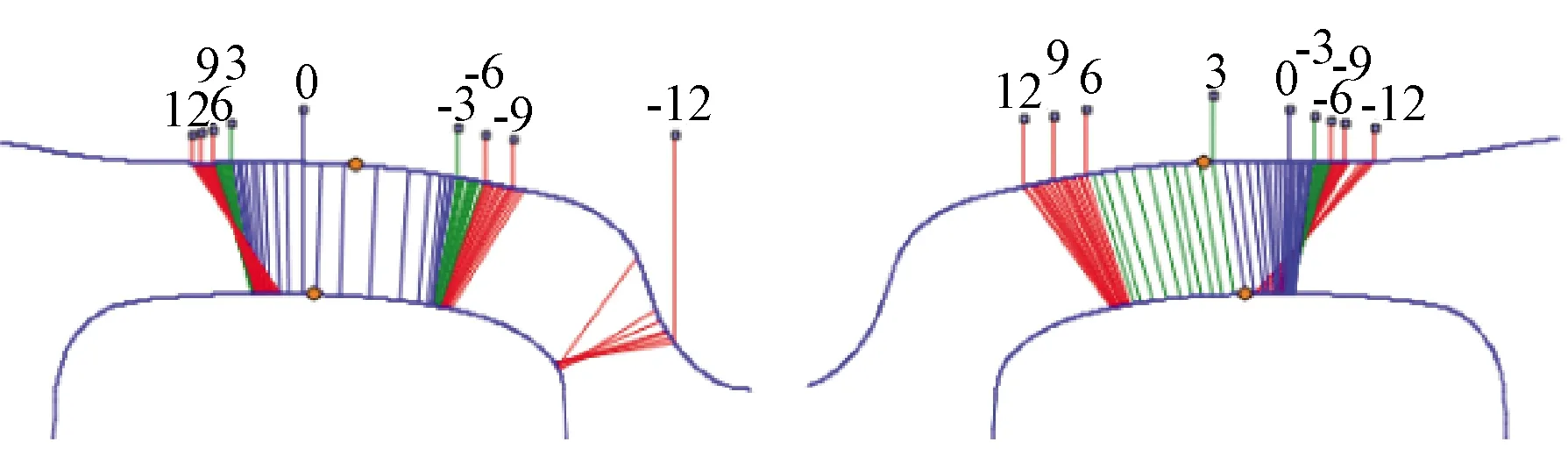
图25 A车轮对与右轨向外移动3 mm后的A轨匹配接触点位置(单位:mm)
综上,2条线路右侧钢轨轨顶位置和左轨头圆角高度的差异对各车辆在跨线运行时等效锥度的变化有较大影响,左侧钢轨左轨头圆角处高度的差异也对跨线运行时等效锥度的变化有一定影响。
5 结论
通过对大量实测车轮和钢轨型面的匹配关系研究,并结合动力学测试结果进行深入分析,得到如下结论。
(1)B线路车辆在A线路上运行时0~3 mm范围内的等效锥度水平较大,造成了B车构架出现幅值较大的横向8.1 Hz谐波振动。
(2)B车轮对与B线路钢轨存在共形磨耗,在左轮踏面60~70 mm和85~90 mm范围内及右轮踏面60~70 mm范围内斜率绝对值高于A车踏面,这些差异是B车在与A轨匹配时1.5 mm等效锥度大于A车的原因。
(3)A车轮对与A线路钢轨存在共形磨耗,其右轮踏面70~80 mm范围内斜率绝对值较B车踏面小,是A车在与B轨匹配时1.5 mm等效锥度略小于B车的原因。
(4)B线路右轨轨顶位置较A线路靠外侧2~3 mm,B线路右轨在轨道横坐标-25~0 mm左轨头圆角处较A线路低,这2点差异对动车组在跨线运行时等效锥度的变化有较大影响;B线路左轨在轨道横坐标-25~-5 mm左轨头圆角处较A线路低也对跨线运行时等效锥度的变化有一定影响。
(5)钢轨廓形的维护打磨非常重要,不同线路之间打磨廓形差异不能过大,特别是要避免各线路钢轨轨顶位置差异过大,不能出现在轨道坐标系下轨头圆角高度不一致的情况,进而保证各车轮踏面接触点位置较为一致,减小镟修末期踏面外形的差异,进一步保证动车组在跨线运行时能够产生良好的轮轨关系,提高动车组的线路适应性。
