疏散通道温度变化与人员流动关系的实验研究——以高校教学楼为例

戎传亮，雷文君，齐新叶

(山东建筑大学热能工程学院，山东济南250101)

0 引言

随着现代社会城市化进程的加快，越来越多的人进入城市工作和生活，各种娱乐、展览等大规模人群活动频繁出现；人们出游的频率也越来越高，尤其是在节假日期间，相关景区的人流量十分密集；火车站、地铁站等公众聚集场所的人员数量急剧地增加，人群密度过大则会因拥挤而产生矛盾，不利于行人流的管理[1－3]，甚至会对人员的生命安全产生威胁。因此，对行人流量的精确统计分析成为各场所管理行人流向不可缺少的重要依据。

随着建筑物越来越多元化，建筑物内的疏散通道和出口也由一个变为多个，但是仍存在疏散通道和出口不均衡使用的现象。 LEI 等[4]通过实地观察发现建筑物的疏散出口存在不均衡使用的现象，从改变建筑结构的想法入手，提出了建筑物疏散出口与疏散楼梯相对位置的改进措施，有助于疏散出口的均衡使用。 但是，如何实现建筑内某个区域人员参数的精确统计一直是国内外相关学者关注的热点问题。 近些年来，国内外学者在人流量的统计方法的研究中做了大量地探索与实践，相关的技术已经应用到生活领域当中。 徐健等[5]对教室图像做了灰度化和二值化处理，进行了中值滤波，再对图像作了二值化形态学分析和运算，通过腐蚀和膨胀算法，获得了可以对人员分布作出有效分析的图像，从而得到对教室人员密度的分析；马海军等[6]和张雅俊等[7]提出一种基于卷积神经网络的人数统计方法，通过卷积神经网络回归图像中人头中心点获得人群密度分布特征图，然后使用岭回归模型分析人群密度分布特征图得到该帧图像对应的人数；吴松等[8]和沈泽等[9]最先引入了一种基于移动网络信令数据的思想来实现对人流量的实时统计；茅飞等[10]以轨道交通车站闸机通道为研究对象，研究闸机通道对过往人员流量的智能识别统计；CHEN 等[11]和许胜强等[12]基于传感器的原理，利用视频、红外传感器、压力传感器、柔性力敏传感器等设备同时监测各疏散通道的人员流量。

上述研究对人员密度及流量的监测具有一定的指导作用和应用价值。 但是，当人员流动相对复杂，且人员较为密集时，这些方法主要存在以下问题:(1) 人数统计准确率下降；(2) 有一定的场景使用限制、效率略低，人们的通行体验往往受到影响；(3) 在现实场景中应用时隐蔽性一般、投资较高且不容易实施等。 而建筑内的环境参数传感器具有体积小、反应灵敏、成本低等优点，能够实时记录人员释放的热量和二氧化碳产物，如果能借助环境参数传感器预测人群密集程度将会事半功倍。 LEI等[13－14]通过现场测试，发现疏散通道内环境的温度与二氧化碳体积分数随着人员流动的快慢而产生相应的变化且在人员流动速度较小时，其变化显著；二氧化碳体积分数与人员流动速度常存在反比关系。进而说明，建筑内的环境参数可以用来反馈人员流动状况，但疏散通道内温度的变化与人员流动状况存在何种关系需要进一步探讨。

利用这一思路，文章针对某高校教学楼各疏散通道开展了实验测试，分析疏散通道内同一时间温度与人员密度变化的关系，以期用温度的变化实现对行人流的预测，获取各疏散通道的使用情况，有助于各疏散通道的均衡使用。

1 疏散通道温度变化与人员流动关系的实验方案设计

1.1 研究对象

监测的区域为教学楼一楼疏散通道，是绝大多数学生上、下课通行的主要通道，短时间内人员密度较大。 监测区域的人员分布在时间上具有一定的规律性，在某些特定的时间段(如上、下课时间段)较为拥挤。 文章将一楼的疏散通道分为了4 个区域(A、B、C、D)，并布设了温度测点 P1、P2、P3、P4，如图1 所示。 通过对同一时间的实测温度数据发现，4个区域的温度随时间的变化规律具有一致性，如图2 所示。 区域B 的温度变化相比其他3 个区域的温度变化较大，因此为避免温度的变化不灵敏以及减小误差，文章仅针对区域B 进行数据监测，分析温度变化与人员密度的关系。

1.2 实验方案

区域B 的结构及测点布置如图3 所示。 为了减少测量数据的误差和随机性，在区域B 内的纵向中轴线上布置2 个温度测点M 和N ，测点高度均为1.9 m、水平间距为1.0 m。 利用2 台空气质量检测仪(TSI 7545)进行数据的监测，其温度的测量精度为±0.6 ℃、温度分辨率为0.1 ℃。 通过2 个测点的温度平均值进行结果分析。 同时，在人员不知情的情况下，采取多角度数码摄像的方式实时录像疏散通道区域B 的人群流动。 测试时间为2019 年4 月8日教学日的上、下课时间段(人员流动相对集中的时间段)，每个教学日上、下课时间见表 1。 选择 7:30 ～8:00、9:20～9:50、12:00 ～12:30、13:20 ～13:50、15:10 ～15:40、16:50～17:20 等 6 个时间段进行实地监测，分别为上课进教室的单向流(7:30～8:00、13:20～13:50)、下课出教室的单向流(12:00～12:30、16:50～17:20)以及上、下课交替的双向流(9:20～9:50、15:10～15:40)。

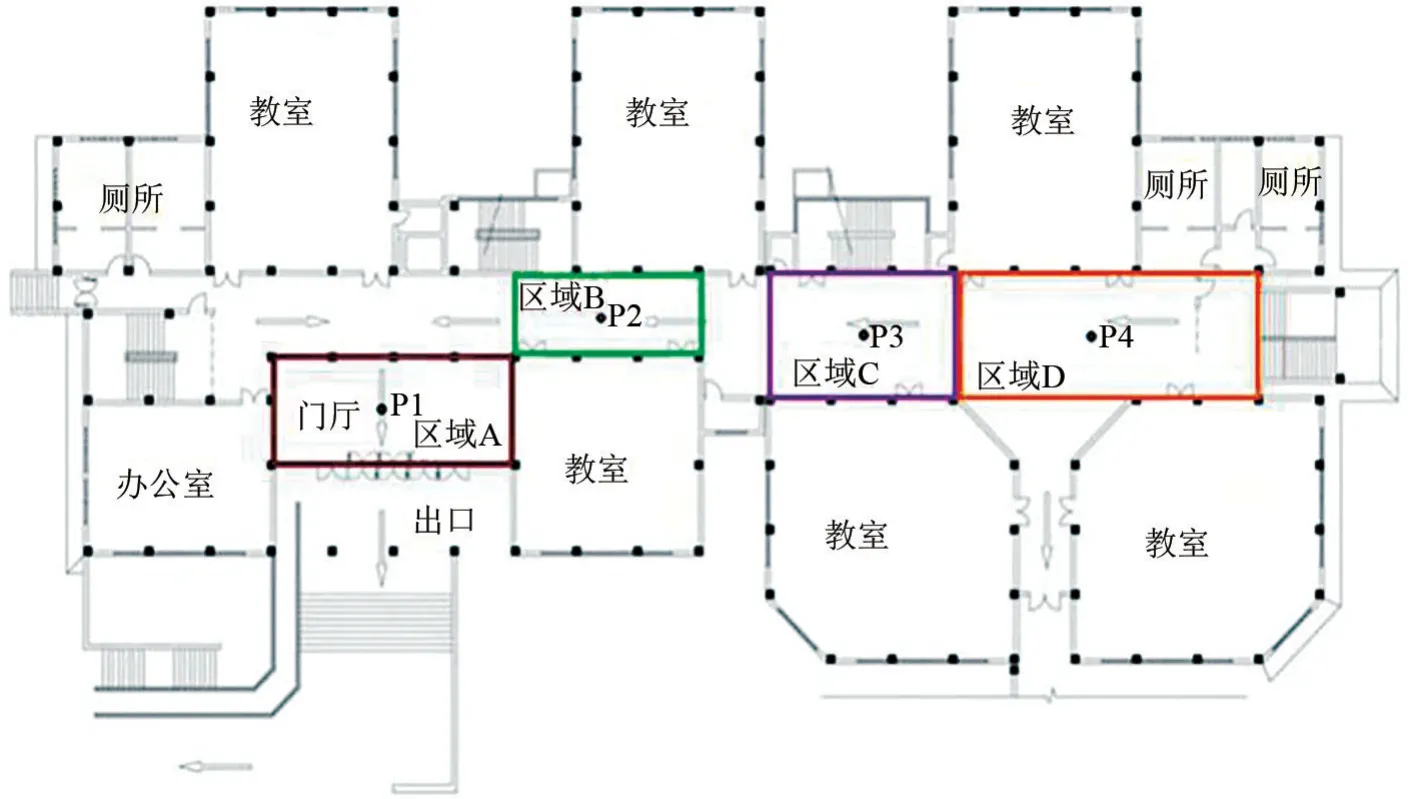
图1 一楼疏散通道建筑结构及区域划分图

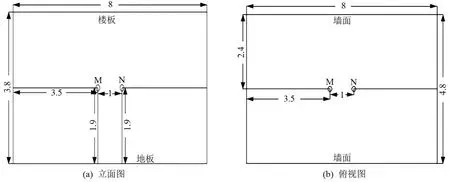
图3 区域B 测点布置图/m

表1 教学日每节课上、下课的时刻表

1.3 实验数据分析方法

1.3.1 人员数量测量的误差分析

用数码相机录制的视频来记录人员数量。 为了保证数据的准确性，对每个视频中的行人计数5 次。行人流量特征通常用行人密度和行人流量表示。 行人密度是指给定时间单位面积的人数，人/m2；行人密度的时间分辨率为5 s；行人流量是指单位时间内通过某一区域截面的人数，人/s。 利用变异系数Cv来反映数据的离散程度。 当需要比较两组数据离散程度大小的时候，如果两组数据的测量尺度相差太大，或者数据量纲的不同，直接使用标准差进行比较不精准，而变异系数能够消除测量尺度和量纲的影响，它是原始数据标准差与原始数据平均数的比。依据《实验设计与数据处理》[15]可知:测试结果的优劣按变异系数值来划分等级，变异系数Cv＜5%为“优等”；5%＜Cv＜10%为“一般”；Cv＞10%为“不良”。变异系数越小，代表其数据的离散程度越小，其平均数的代表性就越好，反之亦然。 人员数量的变异系数计算由式(1)表示为

式中σxi为测量人数的标准误差，人；为测量平均值，人。

测量人数的标准误差由式(2)表示为

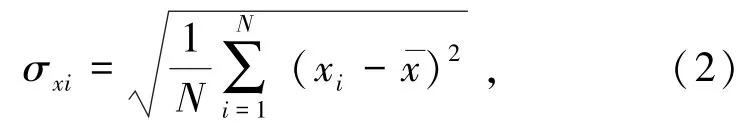
式中xi为直接测量值，人；N为测试数，次。

根据式(1)和(2)计算得到人员数量的变异系数Cv为4.65%，可知数值处在“优等”范围内，故可以忽略此误差对测试结果的影响。

1.3.2 疏散通道内空气温度分析方法

室内疏散通道内的空气热平衡方程文字表达式为:墙体内壁与空气的对流换热量＋通风得热量＋人体显热散热量＝单位时间内室内空气中显热量的增值，可由式(3)表示为

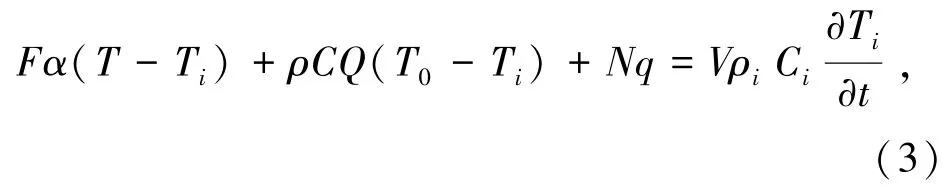
式中F为墙体总面积(不包括门窗面积)，m2；α为室内空气与墙壁的对流换热系数，W/(m2·K)；T为墙体内表面空气温度，K；Ti为室内测试点空气温度，K；T0为室外空气温度，K；ρ为室内空气密度，kg/m3；ρi为室内测试点空气密度，kg/m3；C为室内空气比热容，J/(kg·K)；Ci为室内测试点空气比热容，J/(kg·K)；Q为通风率，m3/s；q为人体显热散热量，W/人；N为行人数量，人；t为通风时间，s；V为室内疏散通道内的体积，m3。

由式(3)可知，室内空气中的温度不仅与行人数量有关，还与围护结构传热、通风率(机械风量、自然风量)、送风温度等变量有关。 为了便于数据分析，文章对式(3)进行了如下简化:

(1) 疏散通道的墙体均为建筑内墙，墙体温度稳定，且与室内空气温差较小，不考虑墙体传热的影响；

(2) 测试过程中未开启机械通风系统，故不考虑机械通风的影响；

(3) 每个测试时间段前5 min 内室内疏散通道的空气温度与室外空气温度的变化情况如图4 所示，这段时间内没有大规模的人员进出测试区域，测试区域的行人密度约为0。

由图4 可知，在行人大规模地进出测试区域之前，室内疏散通道中空气的温度波动较小或接近稳定。 这可能是由于测试区域没有与外部直接相通的门窗，室内环境参数温度受室外环境参数变化的影响较小。 因此，忽略自然通风对室内疏散通道内空气温度的影响。 但是，如果建筑疏散通道内有与外部直接相通的门窗，则需要考虑自然通风率的影响。自然通风对室内空气温度的影响需要通过有限条件(可控)实验进一步研究和探讨。

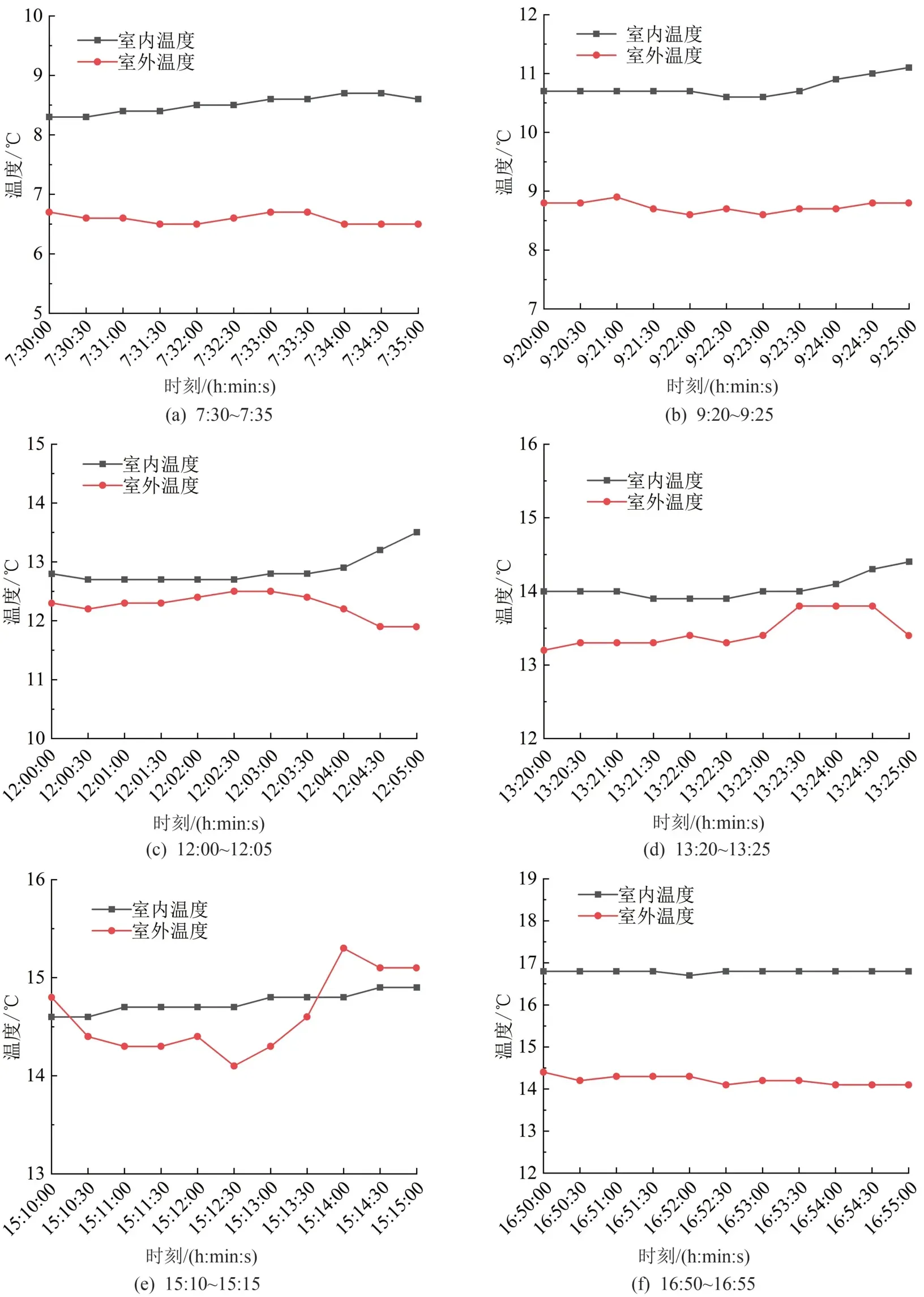
图4 室内温度与室外温度随时间的变化图

2 实验结果与分析

2.1 7：30～8：00 和 13：20 ～ 13：50 时间段温度与人员流动关系分析

7:30 ～ 8:00 和 13:20 ～ 13:50 是学生单纯上课前的时间段，人员流动为进入教学楼的单向流，人员密度较小，如图5 所示。 通过对测试数据的分析，得到了两个时间段温度和人员密度随时间的变化曲线，如图6 所示。 由图6 可知，这两个时间段人员密度随时间的波动幅度较大、规律性较差。 这可能跟学生上课前出行的时间较为分散有关，人员密度的最大值约为0.3 人/m2。 温度波动的幅度较小，整体的规律性较强，两者的变化规律是先增大到峰值后再下降到接近初始状态。 由于人员密度较小、波动太大，在这两个人员流动较为随机的时间段，很难得到温度变化与人员密度之间的定性关系。

图5 教学楼B 区域的人员流动情况图

图6 温度和人员密度随时间的变化图

2.2 12：00～12：30 和 16：50 ～17：20 时间段温度与人员流动关系分析

12:00～12:30 和 16:50 ～17:20 这两个时间段的人员流动为下课出教室的单向流，如图7 所示。由于下课时间的一致性，大量的人员几乎是同步走出教室，人员活动时间较为集中、随机性小，温度和人员密度随时间的变化曲线符合高斯分布。 疏散通道的人员密度在下课后1 ～3 min 内达到了峰值，其峰值人员密度分别为3.5、4.0 人/m2，如图8 所示。随后温度也达到了峰值，12:00～12:30 时间段，温度升高了 4.2 ℃；16:50 ～17:20 时间段，温度升高了1.4 ℃。 温度达到峰值的时间要滞后，温度曲线斜率最大的时刻是人员密度刚好达到最大值的时刻；温度达到峰值的时刻为人员密度降到最低值的时刻；温度升高的过程为人员由聚集状态转为分散状态的过程。 这两个时间段，人员密度和温度随时间的变化规律具有一致性。 人员的流动引起了温度的变化，温度的变化也可以体现人员流动的状态，以此可以根据温度的变化判定出疏散通道的人员密集程度。

图7 教学楼B 区域的人员流动情况图

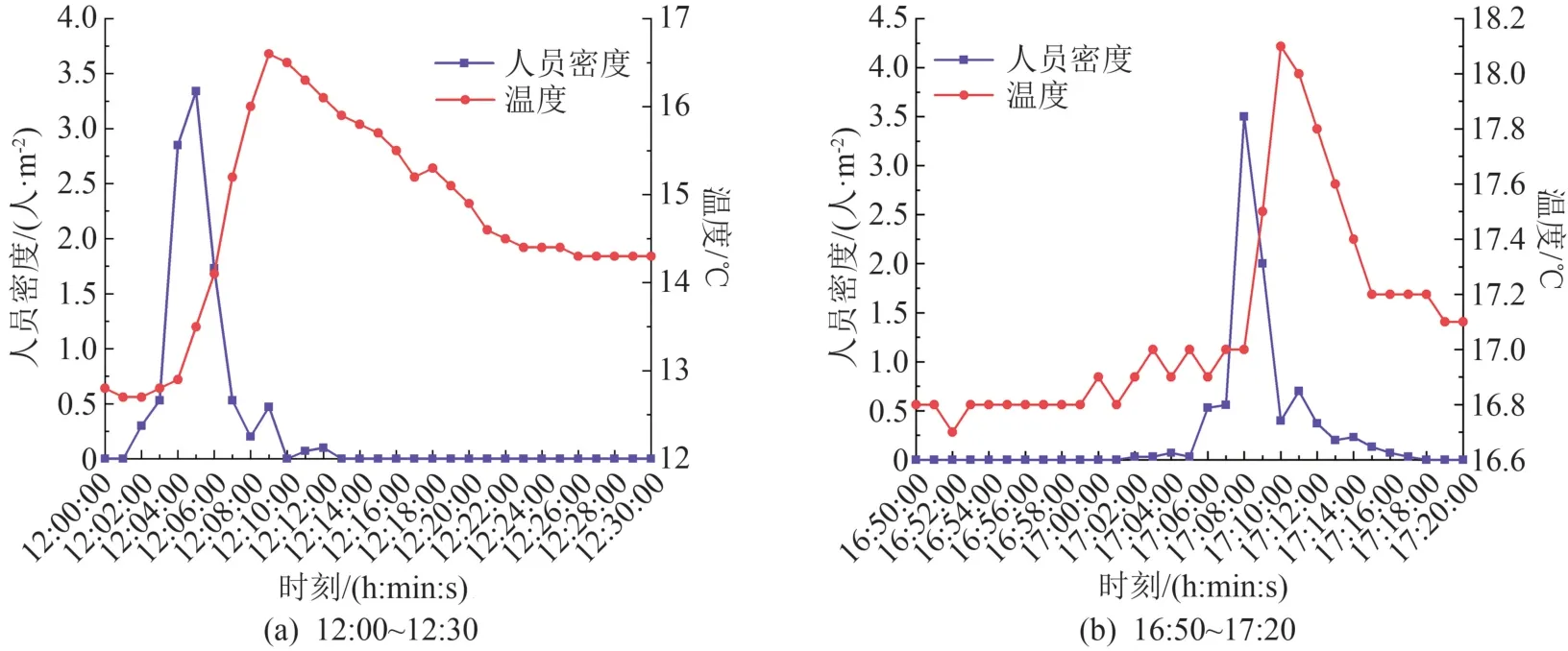
图8 温度和人员密度随时间的变化图

2.3 9：20～9：50 和 15：10 ～ 15：40 时间段温度与人员流动关系分析

9:20 ～ 9:50 和 15:10 ～ 15:40 这两个时间段是上下课交替的时间，特点是人员数量较多，上、下课人员在同一时间开始流动，上课的人员进入教学楼的时间随机性较大，人群存在双向逆流动，如图9 所示。 由于下课时间的一致性，人员几乎是在同一时间开始走出教室，人员活动时间较为集中，随机性小，温度和人员密度随时间的变化曲线同样也符合高斯分布。 疏散通道的人员密度在下课后1～2 min 内达到了峰值，其峰值人员密度分别为3.5、2.7 人/m2，如图10 所示。 随后温度也达到了峰值，9:20 ～9:50时间段，温度升高了5.9 ℃；15:10～15:40 时间段，温度升高了2.1 ℃。 温度达到峰值的时间要滞后，与2.2 所得出的结论具有一致性。 同时也说明，对于人员活动时间集中、随机性小的人员密集性建筑，利用温度的变化来判定人员的密集程度是合理的。 在实际应用中可以通过设定温升界限ΔTmax来判定疏散通道的人员密集程度。 如果温升超过ΔTmax还未达到峰值温度，说明人员还在持续疏散，同时也暗示了疏散通道初始状态的人员较为密集，不易疏散；反之，疏散通道的人员较为分散，较容易疏散。

图9 教学楼B 区域的人员流动情况图

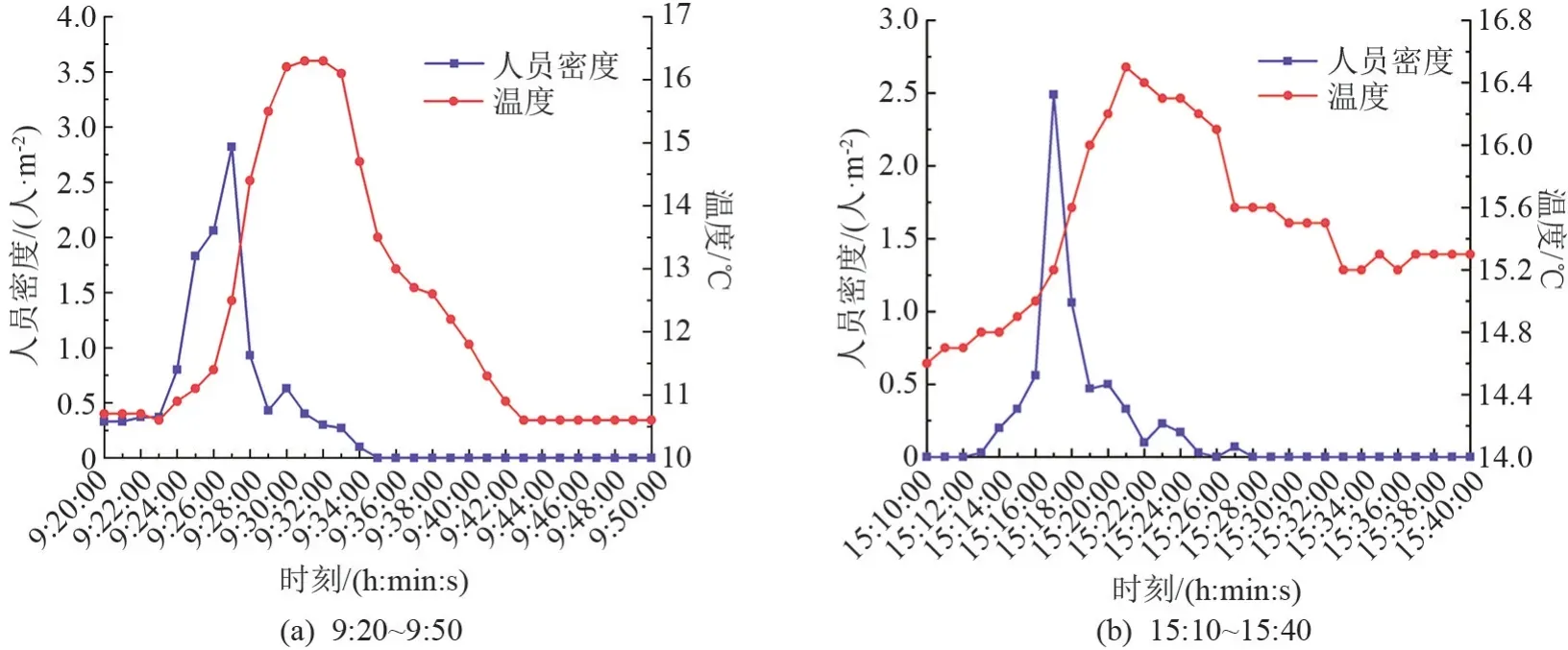
图10 温度和人员密度随时间的变化图

3 结论

通过现场实测教学楼一楼大厅B 区域6 个时间段的温度和人员密度、数据分析，得到如下结论:

(1) 疏散通道内的环境温度会随着人员密度的变化而产生相应变化。 当行人进入建筑物疏散通道的时间随机性较大时(7:30 ～8:00 和 13:20 ～13:50时间段)，人员密度较小(＜0.3 人/m2)，温度的变化不灵敏，人员密度和温度随时间的变化规律性较差，难以得到温度变化与人员密度之间的定性关系。

(2) 当绝大多数行人同一时间进入建筑物的疏散通道时(12:00～12:30、16:50 ～17:20、9:20 ～9:50和15:10～15:40 时间段)，人员密度较大(最大时达到4 人/m2)，温度的变化较为灵敏，人员密度和温度随时间的变化趋势有着较强的相似性，两者随时间的变化规律基本符合高斯分布，且温度的变化总是滞后于人员密度的变化，滞后时间约为4 min，即温度曲线斜率最大的时刻是人员密度刚好达到最大值的时刻，温度达到峰值的时刻为人员密度降到趋向0 的时刻。 温度升高的过程为人员由聚集状态转为分散状态的过程，疏散通道内的温度变化可以判定人员的密集程度。