螺旋管内幂律流体流动换热数值模拟

张浩，陈为花，包晓琳，玄克勇

( 1.山东建筑大学 热能工程学院， 山东 济南250101；2.山东省绿色建筑协同创新中心，山东 济南 250101；3.青岛腾远设计事务所有限公司，山东 青岛266100；4.山东林李建筑设计有限公司，山东济南250014 )

0 引言

幂律型非牛顿流体作为驱油剂具有高黏度、低热导率的特性，其驱油效果比普通水驱要更好，其已在石油开采工程中得到了广泛的应用。 螺旋形通道相对于常规直管通道，其剪切降解作用小，管内聚合物溶液处于高黏度下，可进一步增加采油量[1－2]。因此，深入探究幂律流体在螺旋管内的流动换热特性是石油开采工程应用的基础[3]，可为实际流动换热技术的研究提供理论依据，亦可满足节能需求。

李玉伟等[4]以非牛顿流体为研究对象，分析了变截面管道中非稳态过程下的流动和换热，发现了相对于普通位置，流体压力和速度波动情况在截面突变区域将更加剧烈。 JAYAKUMAR 等[5]研究了螺旋管直径、螺距等几何尺寸对管道内流动与换热的影响，并通过解析法回归得到无量纲参数努塞尔数计算式。 PIMENTA 等[6]在实验过程中保持管道壁面温度恒定，通过改变内径、曲率、长度、螺距等因素，发现螺旋管内层流流动工况下牛顿流体与非牛顿流体传热系数变化规律。 PAWAR 等[7]分别采用实验方法和数值仿真方法对比了螺旋盘管换热器内牛顿流体、非牛顿流体的换热过程，并通过回归分析获得两种介质阻力系数和传热系数关联式。 郭松灿等[8]模拟研究了正弦通道流动换热问题，并基于双电层作用，针对幂律流体使用高精度紧密差分格式建立相应的质量方程、动量方程和能量方程，研究幂律指数和粗糙度变化对通道内对流换热过程的影响。 PITAK 等[9]模拟了不同形式的螺旋椭圆管流动与传热特性，在湍流状态下获得椭圆管深度比和椭圆管节距比与流动换热间的关系，进一步在相似条件下得到典型螺旋椭圆管比交错式螺旋管和规则间距螺旋椭圆管传热速度快的结论。 陈贵冬等[10]运用仿真软件Fluent 建立了基于螺旋管通道和直管通道对比的混合计算模型，分析探讨了不同螺旋角度，获得了螺旋通道强化换热效果最好的螺旋角值，并通过传热努塞尔数的形式进一步描述了两种管道内传热情况。

文章选用工程常用幂律流体羧甲基纤维素水溶液作为流动介质，参照实际非牛顿流体复杂物理性质，设定研究介质黏度、热导率为随温度变化的变物性参数，建立模型并验证网格划分和独立性，运用流体力学仿真软件CFX 模拟研究了螺旋管内非牛顿幂律流体流动阻力和传热特性，针对3 种不同螺旋管道流动工况、结构参数和相对粗糙度分析了沿程阻力系数和传热努塞尔数的影响。

1 模型建立

1.1 物理模型

为研究幂律流体螺旋管内流动特性及换热特性并针对管道结构进行优化分析，综合考虑螺旋半径、曲率等影响因素，设计了3 种螺旋管经典管道模型，具体尺寸参数见表1，几何模型如图1 所示。

表1 物理模型尺寸参数表

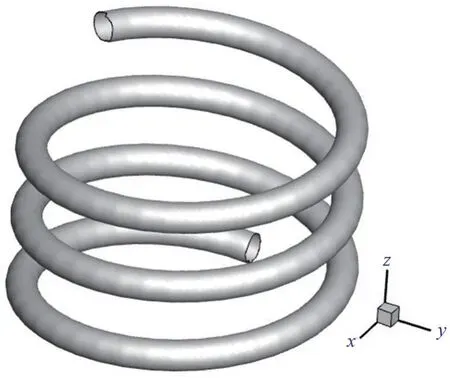
图1 螺旋管几何模型图

1.2 数学模型

控制方程是以数学表达式形式描述流体流动传热过程中所遵循的守恒定律。 所有的流体运动包括幂律型非牛顿流体都满足流体动力学基本方程，其通用形式由式(1)[11]表示为

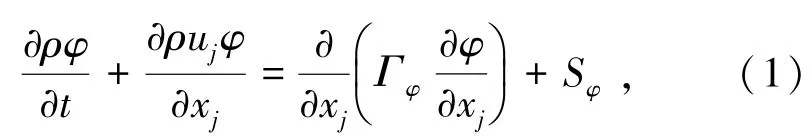
式中φ为通用变量，代表单相守恒特性，可以替换成分速度、温度或常数量；ρ为流体密度，kg/m3；t为时间，s；uj为单相速度矢量，m/s；Γφ和Sφ分别为扩散系数和源项。

湍流过程是非稳态且规模较复杂的一种流动状态，从流动过程看不仅是流体随时间变化的函数，还是在流动区域内随空间波动的函数。 螺旋管道内湍流流动采用湍流模型RNGk－ε模型和壁面函数法描述，RNGk－ε方程[12]由式(2)和(3)表示为

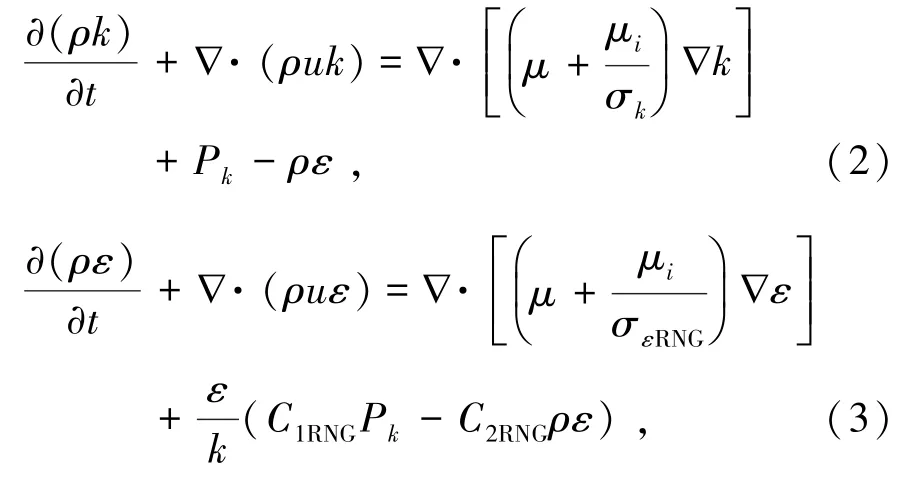
式中k为湍动能项，用来描述速度波动变化量，m2/s2；ε为湍动能耗散项，表示单位时间湍动能变化，是速度波动耗散速率，m2/s3；∇为哈密顿算子；u为x、y、z方向速度矢量，m/s；μ为流体动力黏度，Pa·s；μi为湍流黏度，取决于湍动能和湍动能耗散量，Pa·s；σk、σε、C1、C2均为常数系数，取值分别为1、1.3、1.44、1.92；Pk为浮力与黏性力的湍流产物，Pa/s；σεRNG、C2RNG均为 RNGk－ε湍流模型常数，取值分别是 0.718、1.68；C1RNG为 RNGk－ε湍流模型系数，取决于流体表观黏度η，C1RNG＝1.42－

1.3 边界条件设置

为保证计算速度和精度，在流体模型软件CFX 中将迭代步数和收敛残差分别设为103和10－6。 循环介质选用质量分数为2%，进口温度为298.15 K 的羧甲基纤维素水溶液，其物性参数设定为:幂律指数n＝0.5、稠度系数K＝3.58 Pa·sn、比热容cp＝4 200 J/(kg·K)、密度ρ＝1 011 kg/m3、导热系数(导热系数常数λ0＝0.6 W/(m·K))、剪应力η＝K·

为简化计算，具体边界条件设定为

(1) 速度入口条件，具体速度值由设定的雷诺数通过文献[13]中公式2.6 计算获得，压力出口条件，相对压力为0；

(2) 常壁温边界条件，螺旋管壁面温度恒定为318.15 K；

(3) 默认设置模型入口处为充分发展段，由入口段长度估算方法[14]计算可知建立的模型入口效应可忽略；

(4) 层流工况设置无滑移壁面条件，湍流工况设置壁面相对粗糙度变化范围为0.000075～0.0333 mm；

(5) 模拟计算区域设为一个标准大气压，P＝101.325 kPa。

1.4 网格独立性验证

为保证计算精度和收敛速度，选用非结构化网格类型为Tetra/Mixed，应用网格生成方法Robust(Octree)对模型进行网格划分[15]。 在近壁处对网格进行加密，设置边界层节点为10 个，可以得到较高质量的网格。 以绝对粗糙度为0.01 mm、湍流流动时的模型 1 为例，分别选取网格数为 17 万、37 万、58 万进行独立性验证，通过网格数量的增减变化获得最佳网格数量值。 通过观察出口位置的温度值变化情况判断网格数量设置是否合格。 网格数量和具体温度值情况见表2。

表2 独立性验证网格设置表

由表2 可知，网格数从37 万数量开始，出口截面处温度值基本不随网格数量变化。 因此，模型网格数量设置为37 万，在保证计算速度的前提下，同时保证计算结果提供较为准确的模拟数据。 模型2、3 与模型 1 网格数一致。

1.5 模拟结果合理性验证

为了验证采用模型的准确性和模拟计算方法的合理性，模拟水在光滑螺旋管中湍流流动过程，将其结果分别与ITO[16]和SCHMIDT 等[17]提出的关联式计算结果进行比较，结果如图2 所示。

ITO 关联式由式(4)表示为

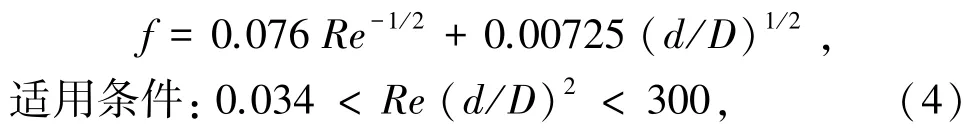
式中f为沿程阻力系数；Re为雷诺数；d和D分别为螺旋管的内直径和螺旋直径，m。

SCHMIDT 关联式由式(5)表示为

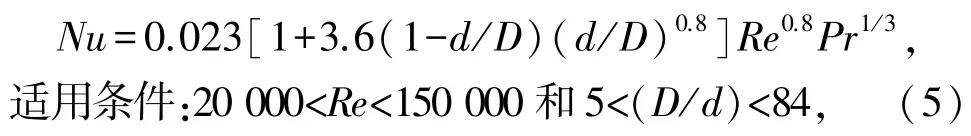
式中Nu为传热努塞尔数；Pr为普朗特数。

由图2 可知，阻力系数、努塞尔数差值变化相对误差分别＜5%和10%，误差范围满足合理性要求，且模拟计算结果与关联式计算结果变化趋势一致，表明采用的数值模拟方法可行。

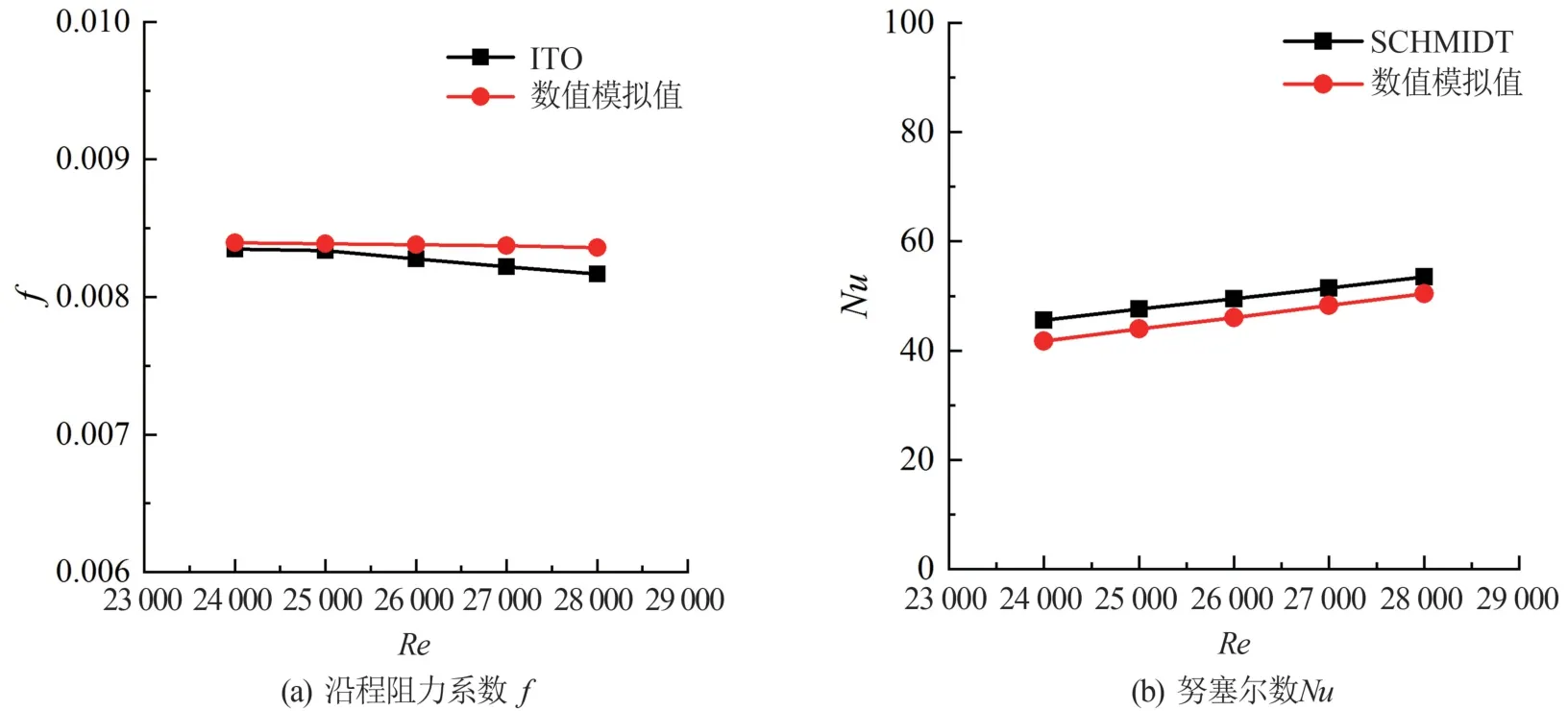
图2 数值模拟与关联式计算结果对比图

2 模拟结果分析

2.1 结构参数影响

为了更为有效地分析幂律流体螺旋管内阻力损失和能量传递，针对不同螺旋管结构建立3 种几何模型(模型 1δ＝0.4；模型 2δ＝ 0.2；模型 3δ＝0.1)，分析常壁温边界条件下螺旋管曲率值和管壁相对粗糙度变化对于流体管内流动过程沿程阻力系数f和传热努塞尔数Nu的影响，通过图表形式直观呈现出两种系数的具体变化情况。

2.1.1 曲率值、粗糙度对沿程阻力系数f的影响

在保证其他条件一致的情况下，针对层流流动过程(Re为 1 000 ～5 000)和湍流流动过程(Re为35 000和45 000)进行数值模拟，得到不同曲率值下沿程阻力系数f，结果如图3 所示。 层流流动时曲率δ变化对沿程阻力系数会产生较为明显的影响，不同曲率值下3 条曲线由上而下分布，曲率值越大沿程阻力系数也越大。 层流流动雷诺数一定时，曲率值越大，沿程阻力系数f也越大；而当曲率一定时，沿程阻力系数f随雷诺数的增大而减小。 曲率增大会增强管道的扭曲程度，进而导致管内流体轴向速度的变化，流动强度减弱，因此管内流体沿程阻力系数增大。 因此，幂律流体在螺旋管内层流流动沿程阻力系数随着雷诺数的增大而慢慢减小。 雷诺数取决于入口流速，其值增大，迪恩数也增大，流动更为剧烈，阻力系数值相应减小。

随着不同属性介质流体在管道内部的流动，往往会造成管内腐蚀或管壁结垢等现象，影响管壁粗糙度，另外不同材料管道光滑程度也不相同，参照实际工程中不同材料表面的绝对粗糙度ks取值范围及尼古拉兹实验值，研究相对粗糙度kx为0.000075 ～0.0333 时管内对流换热特性。 其中，kx＝ks/d1(d1为螺旋管道内直径)。

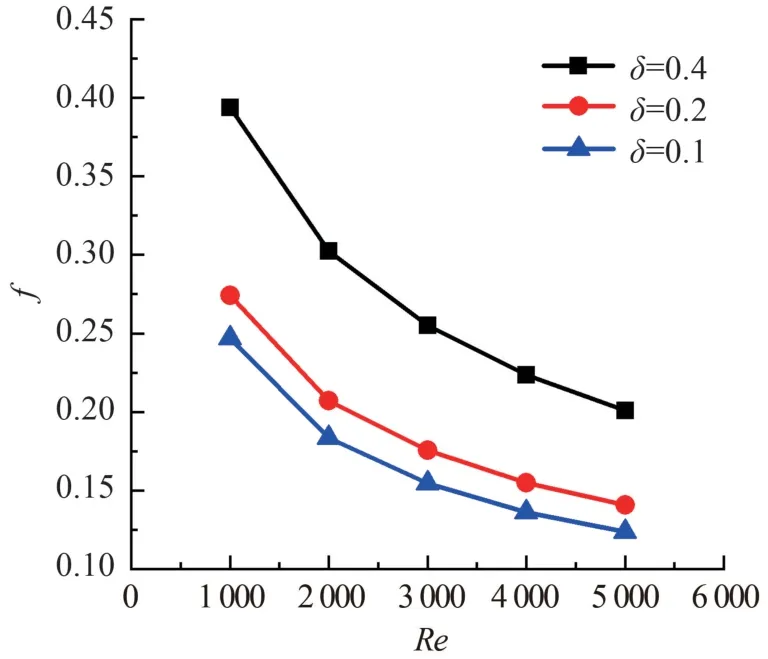
图3 层流时曲率值δ 对f 影响图

在其他条件不变的情况下，以Re数分别为35 000、45 000 时湍流流动情况，对 3 种模型(模型1、2、3 的曲率值分别为 0.4、0.2、0.1)在相对粗糙度在0.000075 ～0.0333 范围时沿程阻力变化进行模拟，结果如图4 所示。 在雷诺数一定时，沿程阻力系数随着曲率值的增大而增大。 对比图3 可知，相对于层流流动，湍流流动扰动作用较强，阻力值较小。对比分析图4(b)中δ＝0.4 和δ＝0.1 时的两条曲线，在粗糙度范围相同时，δ值大的螺旋管阻力系数f的变化幅度约为0.05，而δ＝0.1 的螺旋管的f值变化不足0.03，曲率值大表明螺旋管弯曲程度大，流道的弯曲加剧了管内流体旋转程度，进而沿程阻力变化范围大。

在相对粗糙度分别为0.000075和0.0333时模拟分析了湍流流动，结果如图5 所示。 在相对粗糙度kx较小时，f与Re曲线越来越低；而相对粗糙度较大时，规律刚好相反。 主要是因为较为光滑的管材，流速增加对流动特性的影响大于管壁粗糙度对其的影响，沿程阻力主要受流速增大作用而降低，其中幂律流体在曲率较大的管道内流动时，受到的阻力作用也大。 同时，在相对粗糙度较小时，δ＝ 0.1 的曲线变化规律与曲率值为0.2 的管道相近，这是因为光滑管材阻力作用主要受流速影响，只有当曲率变化较大时，其作用规律才会比较明显。

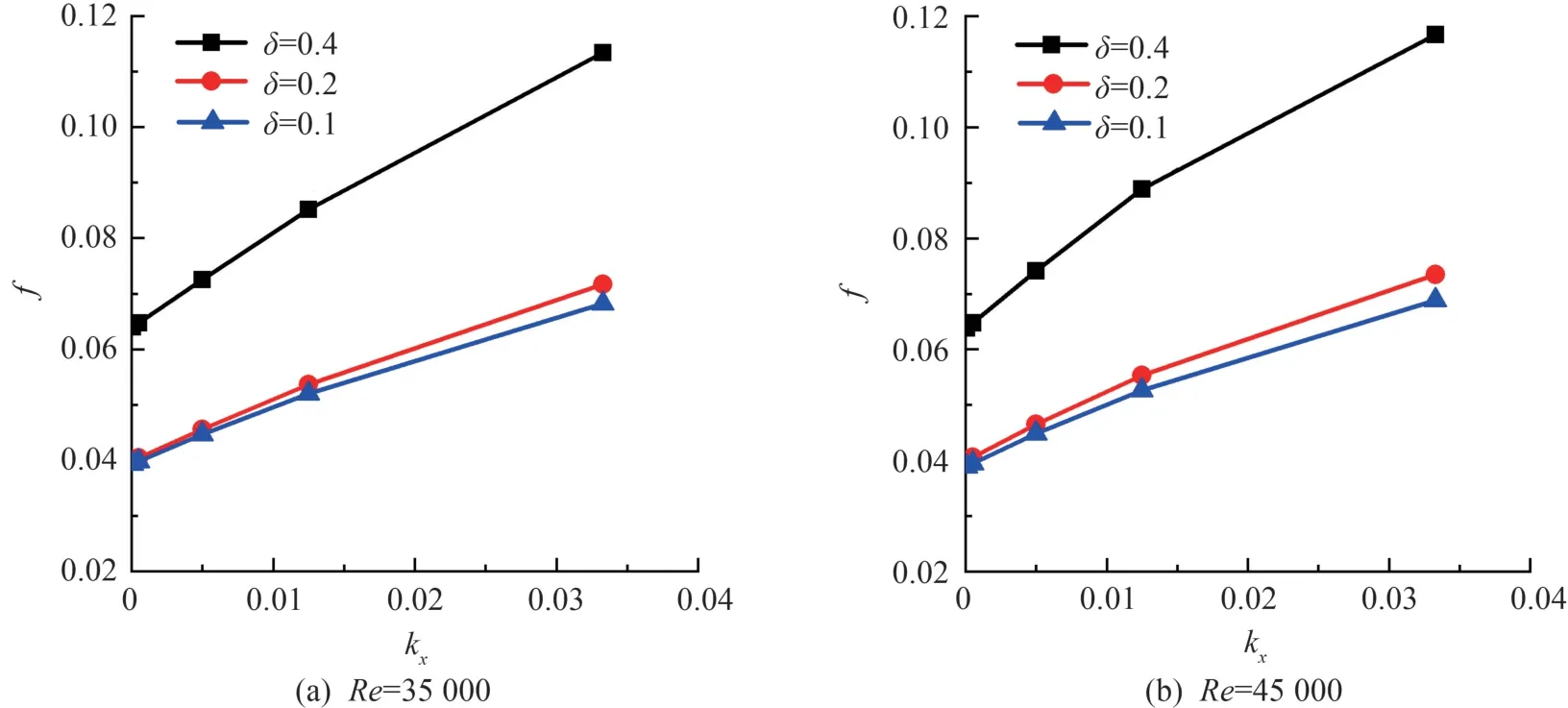
图4 湍流时不同雷诺数下曲率值对f 影响图

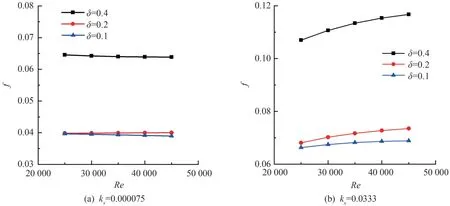
图5 湍流时不同相对粗糙度下曲率值对f 影响图

2.1.2 曲率值、粗糙度对努塞尔数Nu的影响

不同曲率值下，幂律流体螺旋管内层流流动过程传热努塞尔数Nu变化曲线如图6 所示，传热效果同时受到雷诺数和螺旋管结构的影响，随着曲率值的增大，Nu不断增大；在雷诺数为1 000 ～3 000时，传热性能增强更为显著，随雷诺数进一步增大(但流动仍处于层流工况)，Nu增加趋势减缓。 与图3 对比发现，层流工况下，δ增加会增大流动阻力，但对传热有促进作用，而提高雷诺数，既可减少能量损失又可提高换热效率。

两种雷诺数下不同相对粗糙度和不同曲率值时，湍流工况下努塞尔数变化曲线如图7 所示。 传热效果与曲率值呈正相关，对比图6 可知:雷诺数和曲率更大时，努塞尔数随相对粗糙度变化幅度更大，其中大曲率值螺旋管的变化更为明显。 雷诺数的增大带来管内流体的湍流强度增加，加剧了对温度边界层的冲刷作用，使得边界层厚度变薄，壁面热阻减小，因此传热效率提高，努塞尔数增大。观察图7(a)和(b)左下部分可以看出，当δ较小(δ＝ 0.1 和δ＝0.2)时，在相对粗糙度较小的区域曲线值相近，因此在较为光滑的管道内，曲率值增加幅度不够大，对传热性能起不到明显改善。 因此工程实际过程中应适当提高曲率值或增大粗糙度。

在不同粗糙度下对3 个模型建立雷诺数与努塞尔数关系曲线如图8 所示。 随雷诺数增加，曲线趋势都上升，因此对于较为光滑的管材，增大流速可以同时降低阻力、提高换热效率。 粗糙度较大时，Nu值也较大，是因为粗糙度大的管壁对流体扰动作用强，管内二次流效果随之变得剧烈，迪恩数变大增强换热，而曲率增大会降低热阻，增强换热。

图6 层流时曲率值对Nu 影响图

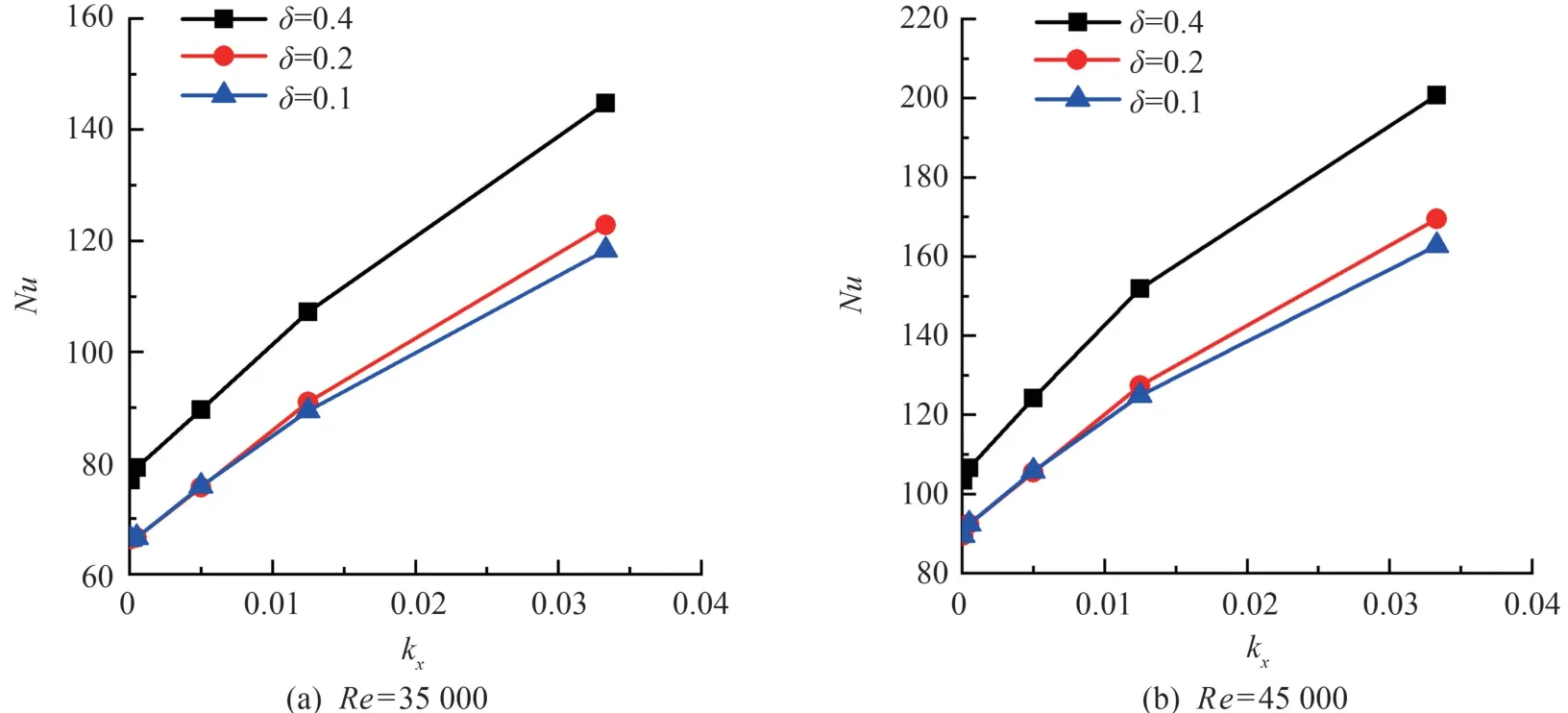
图7 湍流时不同雷诺数下曲率值对Nu 影响图

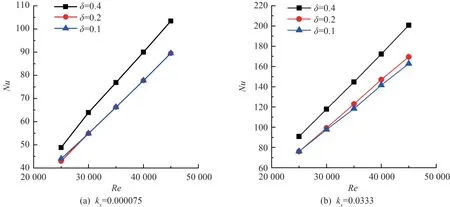
图8 湍流时不同相对粗糙度下曲率值对Nu 影响图

2.2 流动工况影响

幂律流体管内流动换热情况除受螺旋管结构影响以外，还会受到流动工况的影响[12]。 对比层流、湍流两种流动过程管内阻力变化和换热效果，并进一步探讨不同管壁粗糙度与流动换热间的关系。 从实际工程材料表面绝对粗糙度出发，主要研究了0.000075、0.0005、0.005、0.0125、0.0333 等 5 种不同相对粗糙度kx下流动工况对流体换热性能的影响。

2.2.1 沿程阻力系数f变化情况

模型1(δ＝0.4)在层流和湍流两种工况下雷诺数对沿程阻力系数f的影响如图9 所示。 由图9(a)可知，层流时随雷诺数增大，迪恩数增加，螺旋管内二次流强度更为剧烈，扰动作用增大，而二次流的能量来源于主流，因黏性作用转换为热量[18]，沿程阻力系数大幅降低，雷诺数由1 000 增加至5 000 时，沿程阻力系数降低49%。 从图9(b)可知，不同相对粗糙度kx下，沿程阻力系数大小不同，整体变化趋势也不同。 管壁相对粗糙度大的管道受到的摩擦阻力较大，因此f值曲线越靠上。 当使用同一材质的管道进行模拟时，流动阻力变化规律与管壁粗糙度密切相关。 当kx＜0.005 时，f值折线变化规律与雷诺数呈反比；当kx≥0.005 时，变化规律刚好相反。在管壁较粗糙时，高雷诺数下流动的幂律流体往往会出现阻碍流动的涡旋现象，增大了沿程阻力系数。因此，实际工程中要综合考虑性能因素和成本高低选取合适的管道材料。

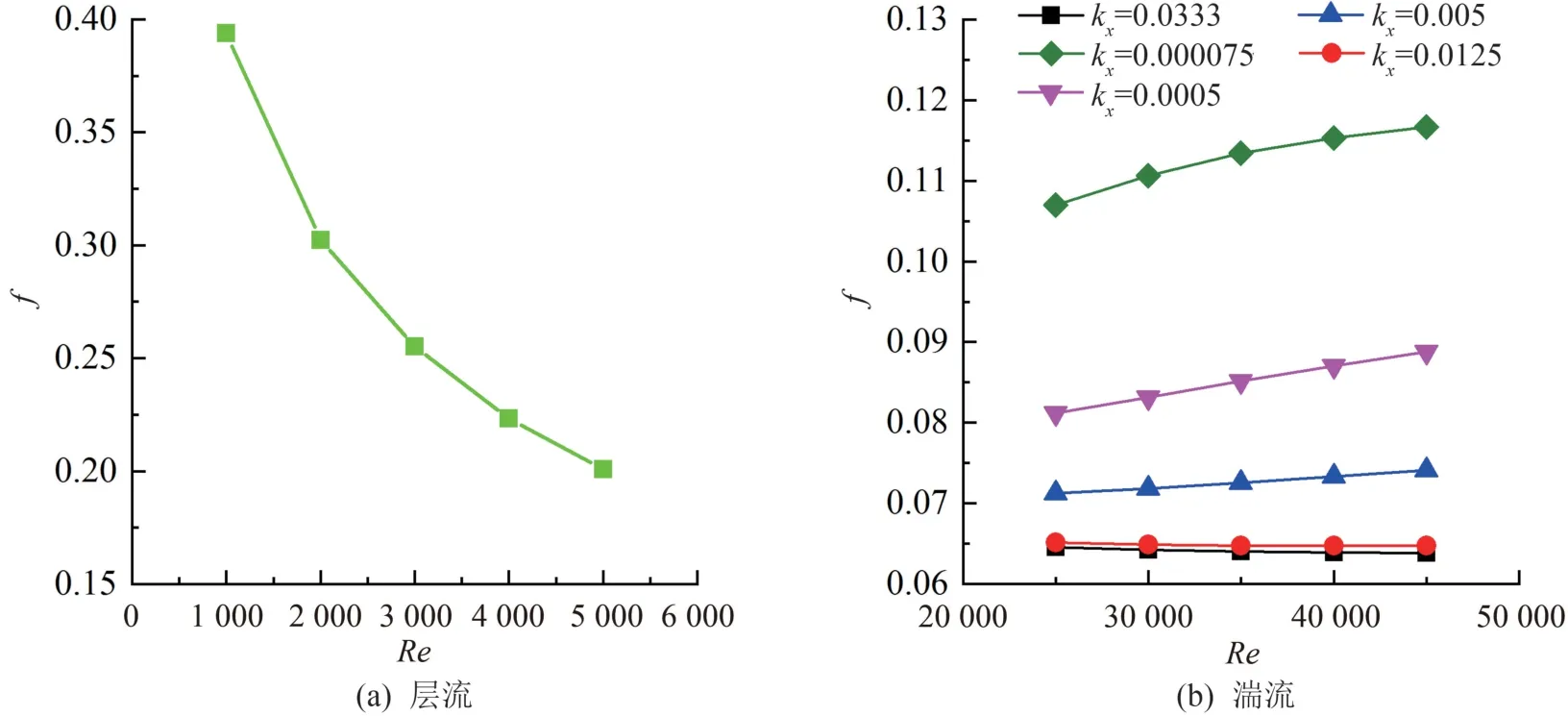
图9 层流和湍流两种工况下f 变化图

模型3 中δ＝0.1 时，雷诺数与沿程阻力系数的拟合曲线如图10 所示。 图10 与图9(b)中不同粗糙度下曲线升降规律相似，但是系数值大小存在一定差异性。δ＝0.4 时阻力作用明显大于δ＝0.1 的情况，进一步验证了具体点曲率变化与管内流动换热机理间关系。

图10 δ＝0.1 湍流工况f 变化图

2.2.2 努塞尔数Nu变化情况

以模型1(δ＝0.4)为例，对不同雷诺数和不同相对粗糙度下换热情况进行模拟，层流与湍流两种工况下努塞尔数变化如图11 所示。 两种工况下，努塞尔数均随雷诺数增大而增大，但是在粗糙度较小时，努塞尔数变化范围也较小。 因此选用比较粗糙的管壁材料或者增大管内流速都可以减弱传热热阻，加强换热效果，提高效率。 由图11(b)湍流工况曲线规律可知:相对于增加流速，改变粗糙度带来的效率提高稍弱，随着雷诺数和粗糙度的增加，材料粗糙度的影响也逐渐增强。δ＝0.1 湍流工况下Nu变化情况如图12 所示。 对比分析图12 和11(b)，在雷诺数较小时，传热努塞尔数变化不明显，而雷诺数较大时，曲率为0.4 的Nu显著增大。 因此，雷诺数和曲率作用共同影响换热机理，且雷诺数大时曲率改变对换热效率影响幅度更大。

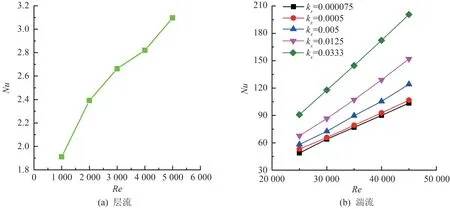
图11 δ＝0.4 层流和湍流工况下Nu 变化图

图12 δ＝0.1 湍流工况Nu 变化图

3 结论

文章通过对幂律型非牛顿流体在螺旋管内流动传热问题进行模拟计算，获得管道内流动换热规律及影响因素，进一步探讨管道内能量损失、压力损失机理，得到如下结论:

(1) 螺旋管曲率值增加，沿程阻力系数增大，传热努塞尔数也增大，但管道扭曲程度增加同样会加强流体与壁面间作用力，扰动的介入一定程度上加强了换热效果。 在雷诺数越小的情况下(层流状态)，增大流速(但流动仍处于层流状态)对努塞尔数影响幅度越大，因此在实际应用中对小雷诺数下流动采取适当增大流速的措施可有效改善换热效果。

(2) 流动状态不同时，对幂律流体管内流动阻力和传热性能也会产生不一样的影响。 层流时，随雷诺数增加，沿程阻力系数逐渐减小而努塞尔数增大；湍流时，除雷诺数外，能量损失还受到管壁相对粗糙度的影响。 当管材较粗糙时，沿程阻力系数在相对粗糙度大的区域随雷诺数增大越来越大，而相对粗糙度较小时规律刚好相反。 这意味着管壁粗糙度过小时，在流速足够大的情况下管内沿程阻力不增反降。 处于湍流流动的流体，增大流速或加大相对粗糙度都可以提高换热速率。