火灾下铝合金梁的温度响应及影响因素分析

王跃兴，谭英华，李艳芹

(1.山东大卫国际建筑设计有限公司，山东 济南250100；2.山东建筑大学土木工程学院，山东济南250101；3.山东鲁科工程质量检测有限责任公司，山东济南250031)

0 引言

铝合金具有自重轻、耐腐蚀性好、强重比高、施工方便等优点，在建筑工程中得到广泛应用，我国很多已建成的跨度和空间较大的网架、网壳和桁架结构建筑，及人行天桥均采用了铝合金结构。 因此，研究铝合金的结构性能具有重要的社会经济意义。 已有很多学者开展了铝合金结构在结构体系、构件设计、材料特性等方面的研究，但现有关于铝合金梁、柱构件，及铝合金网壳结构等的研究多集中在其常温下的结构行为及力学性能等方面[1－8]。

铝合金材料为温度敏感性材料，且其导热系数较高、熔点也很低(580 ～ 650 ℃)。 在 300 ℃ 时，铝合金的屈服强度迅速减半；而火灾下燃烧温度一般可＞800 ℃，此时其结构强度已经完全丧失。 铝合金结构建筑一旦发生火灾，其承载能力将迅速降低，且在短时间内造成结构整体的破坏，甚至倒塌。 因此，对于采用铝合金材料的建筑结构，须进行必要的抗火设计。

关于火灾下结构抗火性能的研究，多集中于钢筋混凝土结构及钢结构[9－12]，铝合金结构方面的研究却较少。 国外在铝合金建筑结构方面的研究已相对成熟，编制了《欧洲规范9:铝合金设计 第1－2 部分:一般规则和建筑物规则》( Eurocode 9:Design of aluminum structures-part 1－2: General rules and rules for buildings，EC9:1－2)[13]供设计人员参考，规范中给出了火灾下铝合金材料强度的折减系数。 随着铝合金结构日益增长的应用需求，我国在铝合金结构抗火性能方面的研究也亟待开展。

文章结合理论和数值分析开展了高温下铝合金受弯构件承载力的研究，依据EC9:1－2[13]并参照《欧洲规范3:钢结构设计 第1－2 部分:结构防火设计通则》(Eurocode 3:Design of steel structure-Part 1－2:General rules-structure fire design，EC3:1－2)[14]，得到不同边界条件下铝合金梁的极限载荷和临界温度，对比有限元软件ANSYS 数值模拟分析结果，验证了有限元计算模型的正确合理性，并通过数值计算分析了跨度对铝合金梁的临界温度、变形及内力的影响，研究了火灾下铝合金梁的弯扭屈曲行为。

1 铝合金梁的有限元分析模型

1.1 铝合金梁材料模型

1.1.1 不同温度下铝合金的弹性模量和屈服强度

常温下 T6061 － T6 铝合金的屈服强度为235 MPa、弹性模量为 70 GPa。 铝合金为温度敏感材料，模拟分析时应采用与温度相关的本构参数。

根据文献[13]规定的不同温度下铝合金的材料性能折减系数确定铝合金的弹性模量、屈服强度。 铝合金弹性模量和屈服强度的折减系数kE，θ、ky，θ随温度变化的情况见表1。 与弹性模量相比，随着温度的升高屈服强度的折减速率较大。 当温度＜200 ℃时，弹性模量折减速率较小；而当温度＞250 ℃时，其折减速率显著增大。

表1 8 种折板网壳结构受力后最大位移值表

1.1.2 热膨胀系数和泊松比

依据文献[13]和[15]，铝合金材料的泊松比取0.3，其热膨胀系数α取 2.3×10－5。

1.2 火灾下铝合金梁的有限元分析模型

利用有限元软件ANSYS 对火灾下铝合金梁的响应行为进行分析。 先采用规范推荐公式计算出常温下铝合金梁的极限载荷，并依据规范得到不同极端约束边界条件下铝合金梁的临界温度，与采用ANSYS 软件计算所得结果进行比较分析，验证火灾下铝合金梁有限元模型的正确合理性。 分析火灾下的铝合金梁的行为时，其过程分为两个步骤加载，即(1) 施加均布载荷或者集中载荷；(2) 施加均匀的温度载荷。

铝合金梁的截面尺寸为H×B×tw×t＝102 mm×66 mm×6 mm×6 mm[16]，如图 1 所示，其中H、B、t、tw分别为截面高度、翼缘宽度、翼缘厚度和腹板厚度。火灾下周围环境的升温曲线采用ISO834 标准升温曲线，假定铝合金梁四面受火，认为温度在铝合金梁的横截面与梁轴线方向是均匀分布的，梁周未采取任何防火措施。 应考虑简支、两端固支、两端铰支及一端固支、一端简支等几种边界条件，如图2 所示，其中L为梁的跨度。 载荷比η＝Mmax/Mu，其中Mmax、Mu分别为载荷作用下铝合金梁的最大弯矩和在常温下的塑性极限弯矩。 根据此公式计算得出的图1 所示铝合金梁常温下的塑性极限弯矩Mu＝11.8 kN·m。

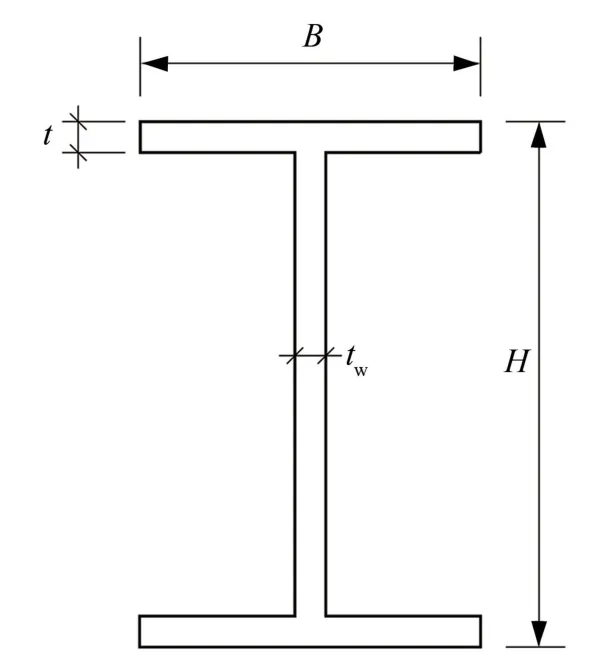
图1 工字型铝合金梁截面尺寸示意图

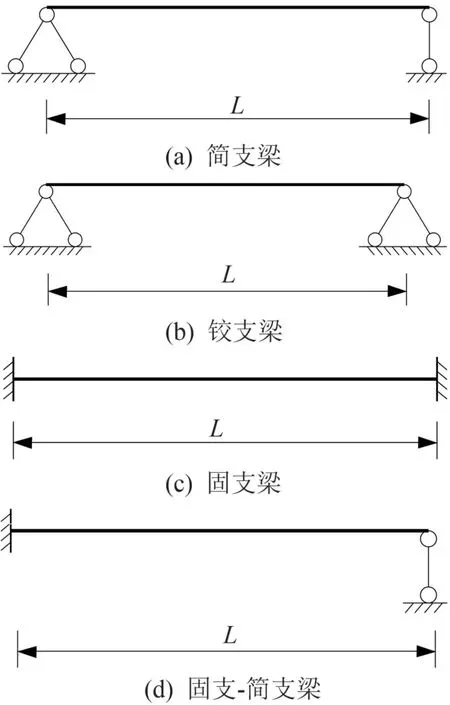
图2 4 种极端边界条件下的铝合金梁示意图

应用有限元软件ANSYS 对铝合金梁进行数值模拟分析，选取适用于细长梁分析的梁单元Beam189 单元。 跨度L＝ 1.8 m 时，将梁划分为 10、20 和30 个单元分别进行模拟计算，两端固支梁跨中作用10 kN 集中力时的温度－位移(T－D)曲线如图 3 所示，其中T为温度、D为位移。 单元数量的改变对温度作用下铝合金梁响应的影响较小，因此将铝合金梁单元数目取为20 个。

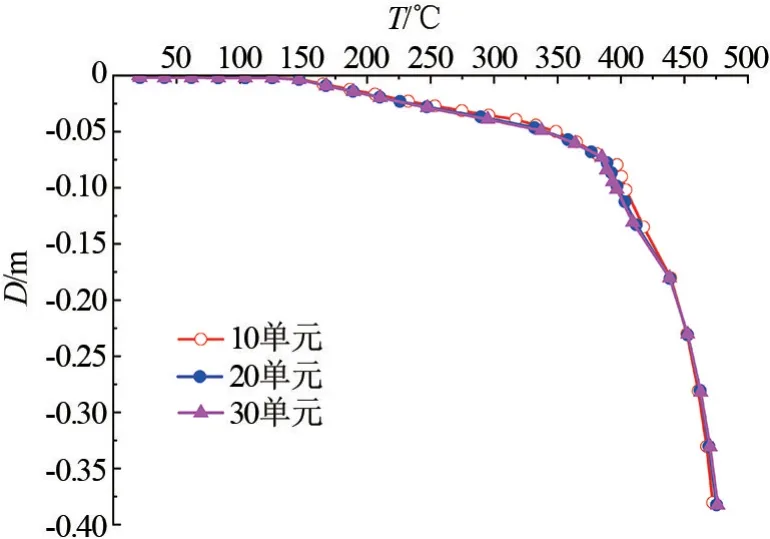
图3 两端固支铝合金梁的T－D 曲线图

2 有限元模型验证

2.1 依据规范计算

在高温作用下当梁上的最大弯矩值等于截面的塑性极限弯矩时，最大弯矩值对应的截面将形成塑性铰，此时梁即达到其承载极限状态，对应的温度为临界温度Tcr。 参照EC9:1－2[13]中的承载力公式求解确定荷载作用下铝合金梁的临界温度，在温度均匀分布的情况下，依据规范，梁的承载力简化计算公式可由式(1)和(2) 表示为

式中Mfi，Ed、Mfi，t，Rd分别为温度为t时梁承受的弯矩和极限弯矩，kN·m；ky，θ值取自表 1；γM1为截面塑性发展系数，值取1.10；γM，fi为火灾下材料的分项安全系数，使用推荐值1.0。

对于截面无洞口削弱、非焊接的铝合金梁，塑性极限弯矩MRd由式(3)表示为

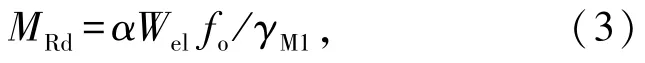
式中Wel为弹性截面模量，MPa；fo为常温下铝合金材料的屈服强度，MPa；热膨胀系数α由式(4)表示为

式中Wpl为塑性截面模量，MPa。

将式(3)和(4)代入式(2)得到梁的极限弯矩，由式(5)表示为

依据铝合金材料的屈服强度及梁的截面尺寸，可求出常温下铝合金梁的塑性极限弯矩MRd；根据式(5)可求出ky，θ，并采用插值计算，求出表 1 中ky，θ所对应的温度，即该工况下铝合金梁的临界温度。

铝合金梁的跨度L＝1.8 m，集中载荷F＝10 kN作用其跨中，利用上述计算方法确定不同极端约束边界条件下铝合金梁的临界温度。 当Mu＝11.81 kN·m、铝 合 金 梁 边 界 条 件 为 简 支 时，Mfi，Ed＝FL/4 ＝4.5(kN·m)，通过式(1)和(5)计算可得ky，θ＝0.42，由表1 通过插值计算得简支边界条件下铝合金梁的临界温度Tcr＝277 ℃；铝合金梁的边界条件为一端简支、一端固支时，梁截面不再存在轴力仅产生弯矩，梁构件随温度的升高将有塑性铰产生，形成瞬变机构，此时Mfi，Ed＝FL/6 ＝ 3 kN·m，ky，θ＝ 0.28，由表 1通过插值计算可得一端固支、一端简支边界条件下铝合金梁的临界温度Tcr＝307 ℃。 两端固支与两端铰支两种极端约束边界条件下，参照GB 51249—2017《建筑钢结构防火技术规范》[17]规定，依据简支梁跨间最大弯矩的原则，将集中载荷等效成均布载荷，Mfi，Ed＝Bnql2/8，Bn为与梁端部约束相关的参数，梁的边界条件为两端固支时，Bn＝0.5，而梁的边界条件为两端铰支时，Bn＝1；q为火灾环境下梁所承受的均布荷载设计值。 求解可得，两端铰支边界条件下铝合金梁的临界温度与简支边界条件下相同，即Tcr＝ 277 ℃；两端固支边界条件下，Mfi，Ed＝FL/8 ＝2.25 kN·m，ky，θ＝ 0.21，求得该边界条件下铝合金梁的临界温度Tcr＝323.8 ℃。

跨中作用集中荷载时，计算极限弯矩Mu的力学公式由式(6)表示为

式中FPu为极限荷载，kN。 根据式(6)计算的简支、两端铰支、一端固支且一端简支、两端固支4 种边界条件下的极限载荷FPu分别为 26.24、26.24、39.36、52.48 kN。

2.2 有限元数值计算结果与规范计算结果对比

通过有限元分析，跨中作用集中载荷时，不同边界条件下的位移(跨中位移)－载荷(D－F)曲线如图4 所示，其中F为载荷。 当载荷值达到铝合金梁的极限荷载时，载荷值不再增加，而铝合金梁的跨中位移仍持续增加，不同边界条件下铝合金梁的载荷－位移曲线的拐点位置对应的荷载即为不同边界条件下的铝合金梁的极限载荷。 由图4 可知，模拟分析所得极限载荷和上述计算结果吻合较好，误差精度均符合要求。 根据GB 51249—2017[17]计算和模拟分析的极限载荷见表2，简支边界条件下模拟分析结果与计算结果相差甚小，两端固支边界与一端固支、一端简支边界条件下的模拟分析结果与计算结果也相差较小。

不同边界条件下铝合金梁的T－D曲线，如图5所示，简支与固支－简支两种极端约束边界条件下的梁，其温度－位移曲线存在明显拐点，将此拐点对应的温度作为梁的临界温度，则两种边界条件下梁的临界温度分别为284、317 ℃，与依据规范计算所得的临界温度相差很小；两端固支边界和两端铰支边界两种条件下，其T－D曲线无明显的拐点，参考EC3:1－2[14]建议，火灾环境下当梁的最大挠度达到时，此时的温度即为梁的临界温度。 有限元模拟分析与采用EC3:1－2[14]规范公式算得的临界温度比较结果见表3，有限元计算得到的临界温度偏高，亦即采用规范建议公式计算得到的临界温度偏保守。

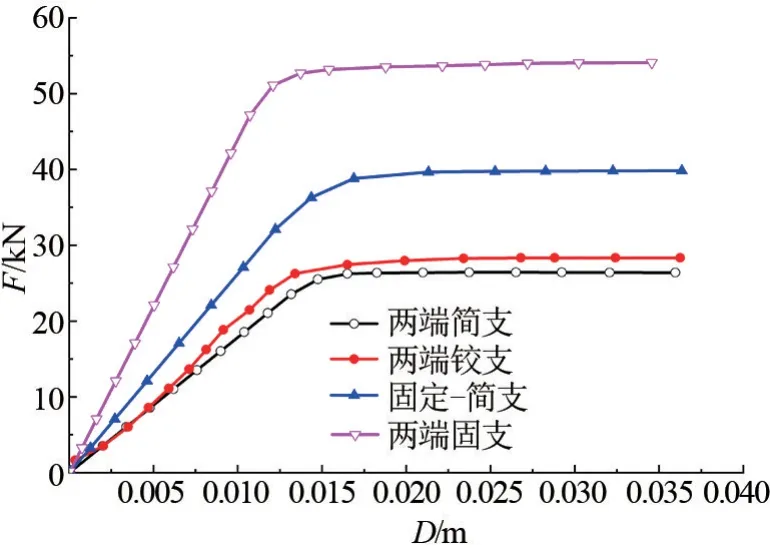
图4 不同边界条件下铝合金梁D－F 曲线图

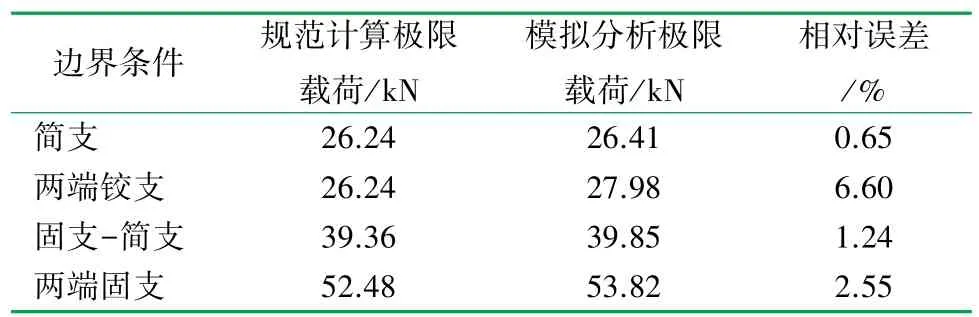
表2 规范计算和模拟分析极限载荷的对比表

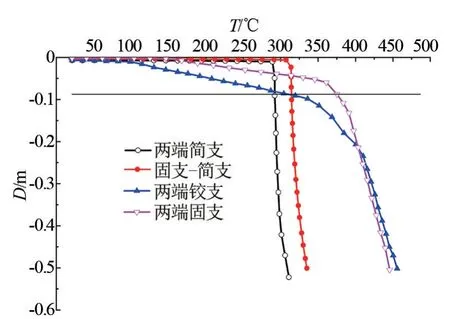
图5 不同边界条件下铝合金梁T－D 曲线图

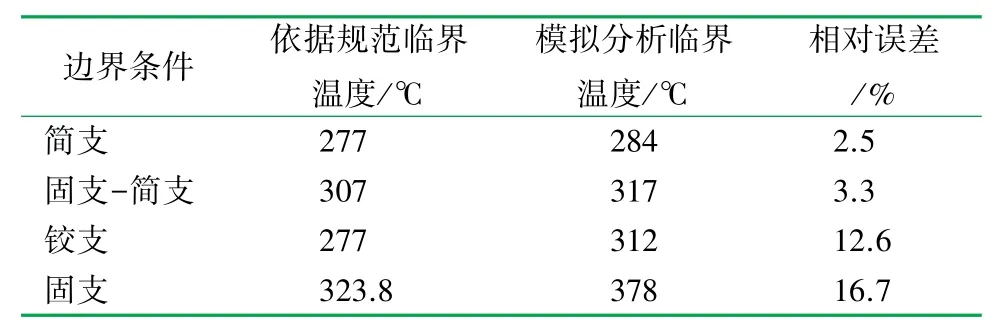
表3 依据规范与模拟分析所得临界温度结果的对比表

通过有限元数值计算，采用上述判别原则，计算得到跨中承受集中载荷和均布载荷的工字型简支梁在不同载荷比下对应的临界温度，与依据EC9:1－2[13]中公式计算出的临界温度的对比结果如图6 所示。 集中荷载、均布荷载两种类型载荷作用下，通过有限元模拟分析所得的简支梁的临界温度与依据规范计算得到的临界温度相差很小，且依据规范计算所得结果偏保守。

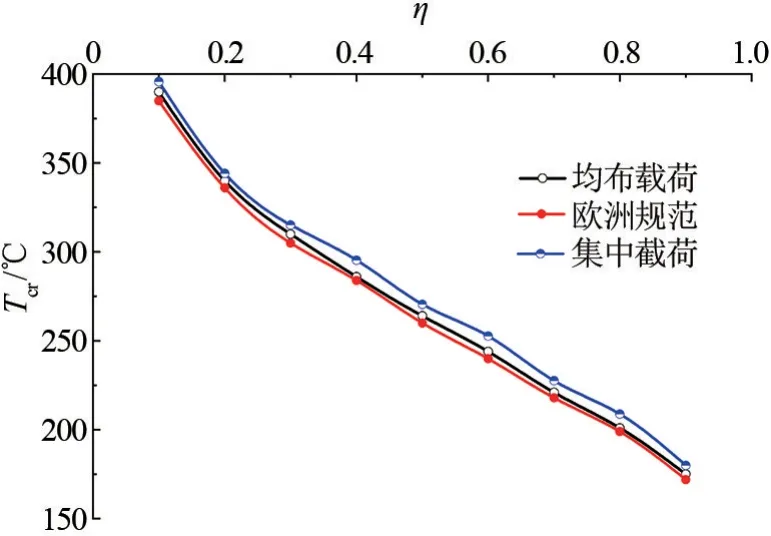
图6 不同载荷下铝合金梁临界温度－载荷比(Tcr－η)曲线图

3 计算结果与分析

3.1 火灾高温下铝合金梁变形及内力温度响应

铝合金梁的跨度L分别取1.8、3 m，作用均布载荷，载荷比η＝0.5，分析跨度对梁变形和内力的影响，得到不同边界条件下的T－D曲线及两端铰支和两端固支两种边界条件下的温度－轴力(T－F)曲线，如图 7、8 所示。

根据图7 分析可知，常温及低温阶段，跨度越大，铝合金梁的位移越大，随着温度的继续升高，位移基本趋于一致，这主要由于常温及低温阶段外力起主导作用，随着温度的继续升高温度占据主导作用。 根据图8 分析可知，铝合金梁的轴向压力随着跨度的增加而减小，其轴向拉力则随之增加，主要原因是梁的跨度越大，其变形越大，进入受拉状态就会越早。

集中载荷作用下，不同边界条件下的铝合金梁的T－D曲线如图9 所示，两端铰支和两端固支两种边界条件下的T－F曲线如图10 所示。 对比集中载荷和均布载荷作用下的T－D和T－F曲线，可以看出，相同边界约束下，虽然载荷的类型不同，但是跨度对铝合金梁变形及内力的影响规律相同，且相应梁的T－F曲线几乎相同，相应的T－D曲线也非常接近。 因此，梁的变形及内力受载荷类型的影响甚微，主要原因是载荷比相同时，外部荷载作用产生的弯矩相同。

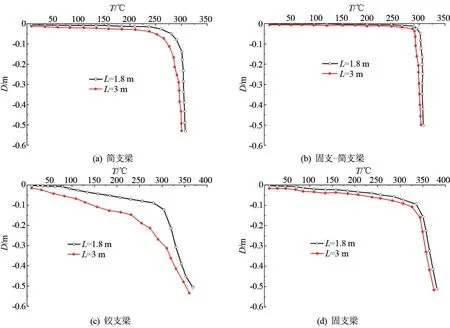
图7 η＝0.5 时承受均布载荷的不同跨度铝合金梁T－D 曲线图

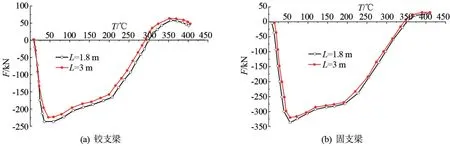
图8 η＝0.5 时承受均布载荷的不同跨度铝合金梁T－F 曲线图

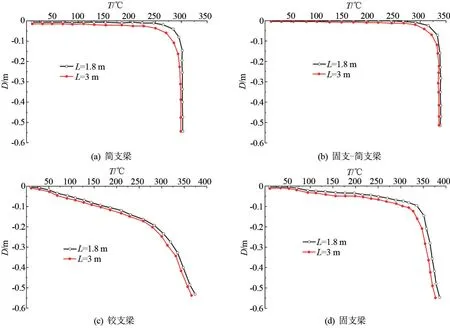
图9 η＝0.5 时承受集中载荷的不同跨度铝合金梁T－D 曲线图

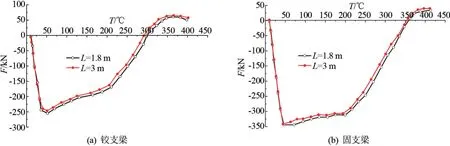
图10 η＝0.5 时承受集中载荷的不同跨度铝合金梁T－F 曲线图

3.2 火灾高温下铝合金梁响应行为的影响因素分析

对于火灾高温下承受均布荷载的铝合金梁，简支与固支－简支两种极端约束边界条件下，其T－D曲线存在明显拐点，将此拐点作为梁的临界温度，由图7 可知，两种边界条件下跨度对梁的临界温度影响很小；对于两端铰支和两端固支两种边界条件，跨中T－D曲线无明显的拐点，参考EC3:1－2[14]建议，将铝合金梁的最大挠度达到L/20 时对应的温度作为其临界温度。η＝0.5 时火灾高温下承受均布荷载的铝合金梁T－D曲线如图11 所示，两端铰支和两端固支的边界约束下，跨度对临界温度的影响较大，其中两端铰支边界条件下两者相差30 ℃，两端固支边界条件下梁的临界温度相差相对减小。 跨度对不同边界约束下铝合金梁临界温度的影响程度不同，其对于无轴力边界条件下梁的临界温度影响很小，对存在轴力边界条件下梁的临界温度影响较大。

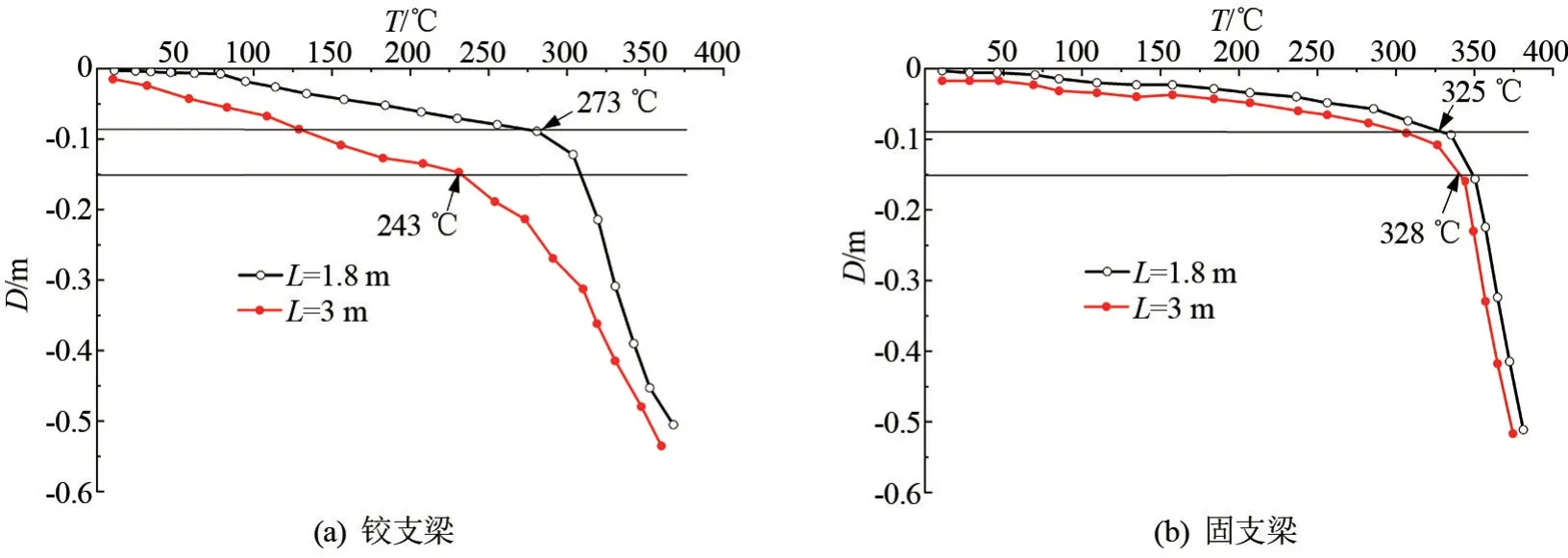
图11 η＝0.5 时火灾高温下承受均布荷载的不同跨度铝合金梁T－D 曲线图

4 结论

通过对火灾高温下铝合金梁响应行为的有限元数值模拟，研究了火灾温度对铝合金梁变形及内力的影响，探讨了临界温度的影响因素，得出以下主要结论:

(1) 常温及低温阶段，跨度越大，铝合金梁的跨中位移越大，随着温度的继续升高，位移基本趋于一致；铝合金梁的轴向压力随着跨度增加而减小，其轴向拉力则随之增加，主要原因为梁的跨度越大，其变形越大，进入受拉状态越早。

(2) 梁的变形及内力受载荷类型的影响甚微，主要原因是载荷比相同时，外部荷载作用产生的弯矩相同。

(3) 跨度对不同边界约束下铝合金梁临界温度的影响程度不同，其对于无轴力边界条件下梁的临界温度影响很小，对存在轴力边界条件下的梁的临界温度影响较大。 梁跨中的温度－位移曲线存在明显拐点时，以此拐点作为梁的临界温度；其温度－位移曲线无明显拐点时，将最大挠度为L/20 时对应的温度作为铝合金梁的临界温度。

(4) 不同边界约束条件下，简支梁的临界温度最低，依据规范计算所得的铝合金梁的临界温度偏保守。