汽车关门声品质预测的MSA-SVR方法研究
2021-06-16黄泽好陈华语邹艾宏陈宝
黄泽好,陈华语,邹艾宏,3,陈宝
(1.重庆理工大学 汽车零部件先进制造技术教育部重点实验室,重庆 400054;2.重庆理工大学 车辆工程学院,重庆 400054;3.重庆金康赛力斯新能源汽车设计院有限公司,重庆 401120)
随着汽车常规性能的提高,其关门声品质也逐渐受到人们重视。汽车关门声品质的优劣直接影响着消费者购车时的决策,因此研究汽车关门声品质具有现实意义。汽车关门声品质研究内容一般包括3个方面:(1)新的关门声品质预测模型研究,加强主观评价与客观评价的相关性,为汽车开发前期提供有效的预测手段[1-2];刘宁宁等[3]建立了基于小波包分解(WPD)和经验模态分解(EMD)的声品质评价模型,并验证了该模型可以准确地预测响度和尖锐度等客观参数。(2)声品质新客观评价参数研究,使客观评价更加真实有效[4]。赵丽路等[5]基于Hilbert-Huang变换,研究提出新的声品质评价参数—SMHHT,并证明该参数与主观评价结果相关性较高,能更准确地评价汽车关门声品质。蔺磊等[6]通过分析汽车关门时尖锐度随时间的变化曲线,提出了与主观偏好值相关性更高的尖锐度溢值作为关门声品质的客观评价参数。(3)汽车关门声品质主观评价体系研究,分析主观评价值与客观参量间的相关性,以提高评价效率[7-8]。其中对于预测模型的研究主要是分析客观参量与主观参量的相关性,而忽略了各客观参量间的相关性。因此,本文针对这一问题提出建立基于多元统计分析-支持向量回归方法的汽车关门声品质主观偏好性预测模型。首先利用因子分析与聚类分析方法得出各客观参量间的相关关系,再根据主观偏好值与客观参量的相关性提取出主要客观参量,运用支持向量回归方法对汽车关门声品质偏好值进行预测,验证该方法对汽车关门声品质预测的有效性。
1 关门声样本采集
在半消声室内,利用人工头、速度传感器、声级校准器等设备,对14辆不同等级乘用车进行等速关门工况下的声样本采集。为保证采样数据的一致性,设置采样频率为44 100 Hz,采样时长为10 s,每组声样本重复采集3次,如图1所示。并将时域采集信号导入HEAD-Artemis软件,剔除声样本中受干扰或采样工况不稳定的信号。根据样本声时长一致性原则,将保留下的声样本长度剪辑为3 s。

图1 试验数据采集
2 主观评价试验
2.1 试验准备及评价过程
根据流程图2进行主观评价试验,主观评价试验选择对评价者无需经验要求的成对比较法。主观评价者为20名(评价者P1~P20)车辆工程专业在读研究生,平均年龄25岁,无听力障碍,且均具有相关噪声与振动知识基础。在听音前对评价主体进行培训,使其了解相关评价内容及方法。
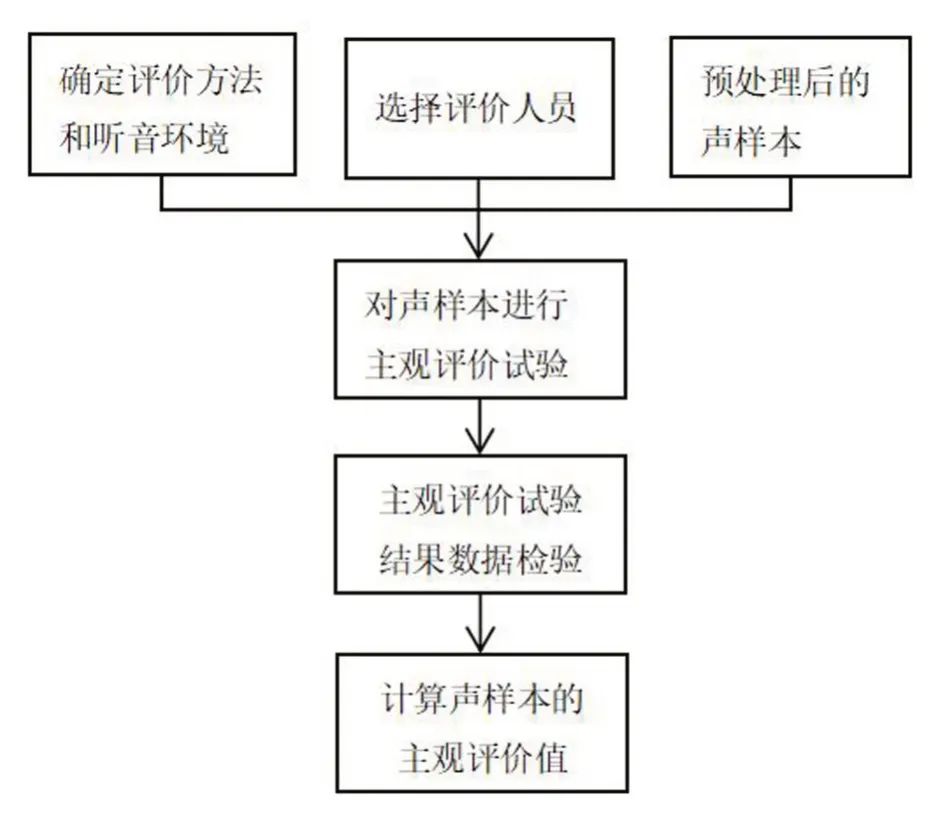
图2 关门声品质主观评价流程
2.2 试验数据处理
为提高试验数据可靠性和有效性,采用交换样本对顺序误判法、相同声样本评价误判法和三角循环误判法对结果进行误判分析。计权一致性系数计算公式如式(1)所示:
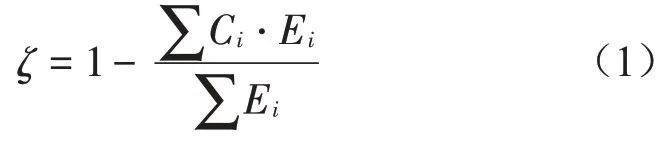
式中:ζ为计权一致性系数,Ci为第i种误判方法实际产生的误判率,Ei为第i种误判分析方法可能产生的误判次数。
由式(1)计算得出各评价主体计权一致性系数如表1。
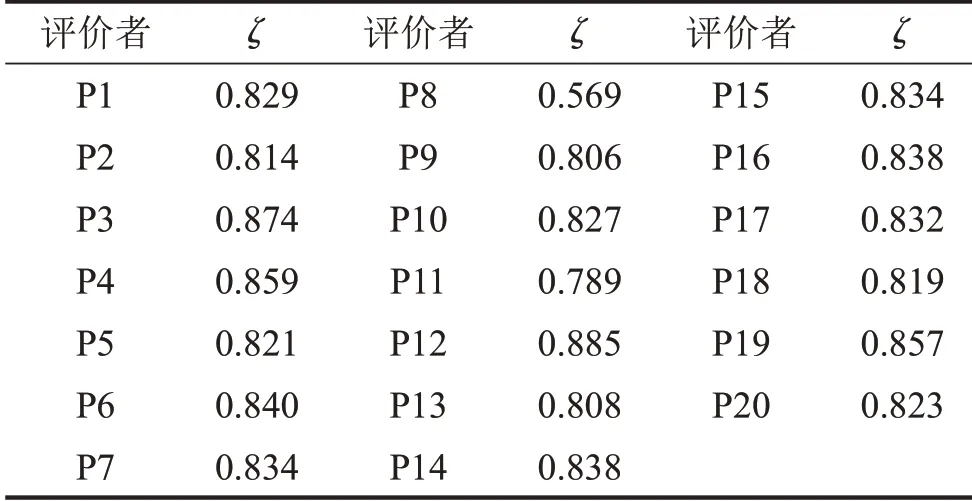
表1 计权一致性系数
根据计权一致性原则,ζ在0.7以上时认为评价结果一致性较好,且最后约10%的评价结果应予以剔除[9]。因此,剔除表1中评价主体P8和P11的评价结果,以确保试验数据的可靠性和有效性。
2.3 主观评价试验结果
以评价主体对样本的选择次数表征主观偏好性得分,并对18名合格评价主体总分值进行算术平均得到14个声样本最终偏好性分值如表2所示。
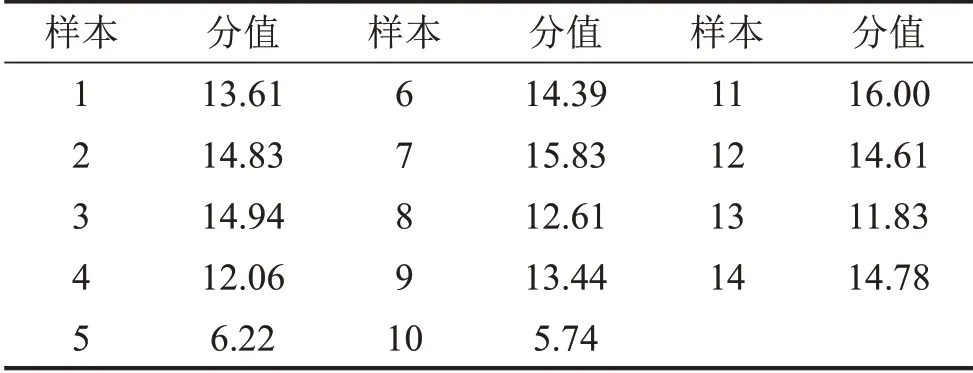
表2 样本主观偏好性得分值
以直方图表示各声样本主观偏好性得分如图3所示。其中,样本11得分最高,样本10得分最低,且由图4、图5两个样本时频图对比可知,样本11在高频时能量较小且能量衰减相对较快,持续时间较短。

图3 各声样本主观偏好性得分对比
3 客观参量计算
心理声学参数可以定量分析不同评价主体听觉感受的差异。应用ArtemiS软件计算得到14个声样本的响度、粗糙度、尖锐度、A计权声压级、抖动度以及语言清晰度,如表3所示。可以看出,各样本客观参量值均有不同,无法预知各客观参量间内在联系且单一客观量无法准确表征样本声品质。
4 客观参量多元统计分析
利用多元统计方法对客观参量进行分析提取[10-11]。首先采用因子分析法与聚类分析法对各客观参量间相关性进行分析,再通过相关性分析得出主观偏好值与客观参量间相关系数,从而提取出与主观偏好性相关系数最高的客观参量。
4.1 因子分析
因子分析可以从多参量中提取出少数客观参量来表征与主观偏好性之间的关系,且这几个参量能够反映主观偏好性的大部分信息。在因子分析法中,原始数据可用矩阵X表示:

则因子模型可表示为X=AF+B,即(3)式:

模型中,n≤m,向量X表示原始观测向量,向量F(f1,f2,f3,…,fn)是X的公共因子,即各个原始观测变量表达式中共同出现的因子,是相互独立的理论变量。公共因子的具体含义应结合实际研究问题来界定。αmn称为因子载荷,是xm与fn的协方差,表示第m个原有变量在第n个因子上的负荷或权重;βm为特殊因子,表示原始变量无法被公共因子解释的部分。采用SPSS数据分析软件对客观参量进行因子分析,分析结果如表4所示。
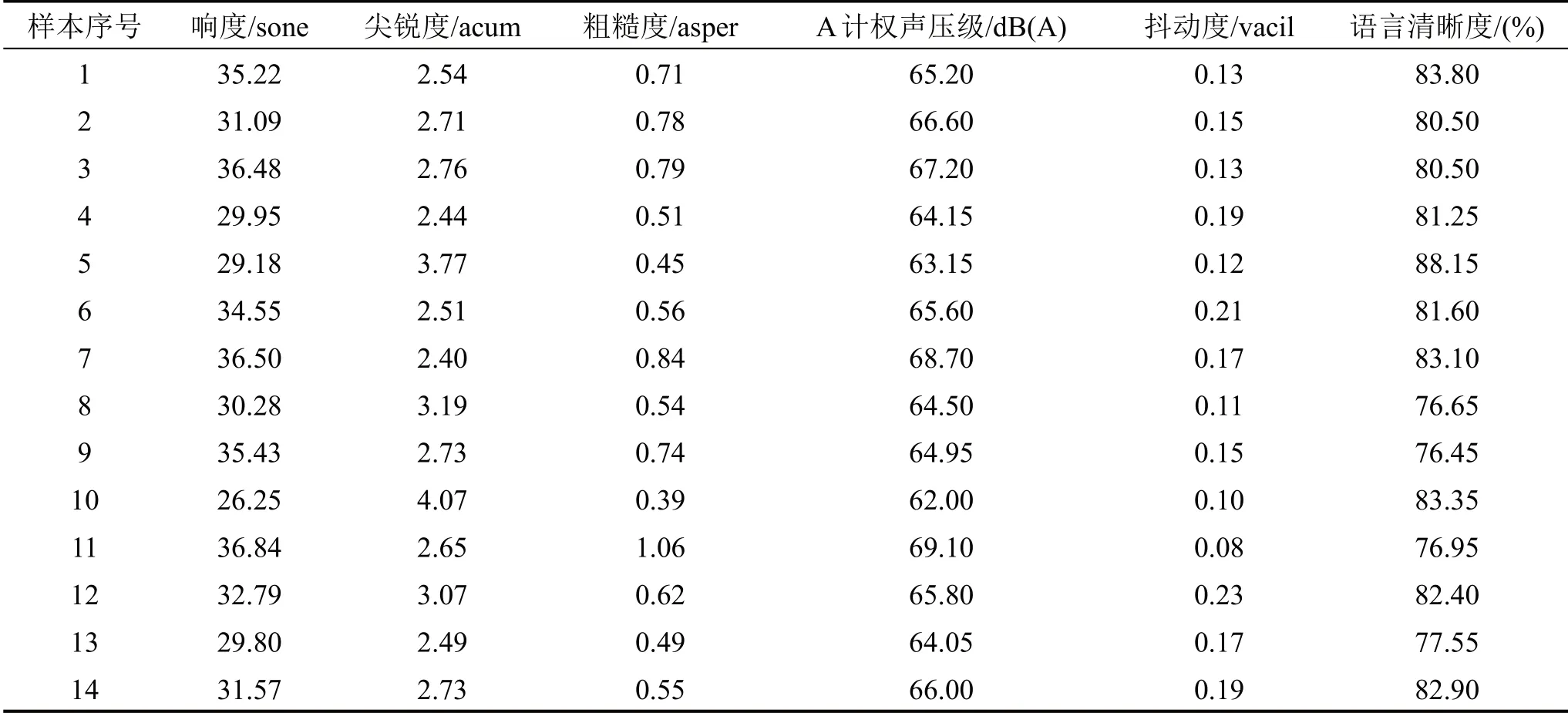
表3 客观参量计算结果

表4 因子分析结果
表4的因子分析结果表明,前3个成分对于6个客观参量(响度、尖锐度、粗糙度、A计权声压级、抖动度、语言清晰度)的解释率已高达92.910%,符合累积贡献率高于85%时可以代表原始信息量的原则[12],说明3个因子可很好体现原始参量的大部分特征,可只提取3个因子用于汽车关门声品质偏好性预测。

图4 样本10时频图

图5 样本11时频图
4.2 聚类分析
聚类分析主要根据数据间的相似性对数据进行分类。本文采用层次聚类法中的最短距离聚类法对客观参量进行聚类分析。设有i个样本,每个样本有j个参量值,原始数据可用如式(4)矩阵Y表示。

其中:yij表示第i个样本的第j个参量的观测值。
将原矩阵元素上下非对角元素中找出,分别定义为Gp和Gq并归为一新类Gr,然后按式(5)和式(6)计算原来各类Gr与任一新类Gk之间的距离:

这样就得到一个新的(m-1)阶的距离矩阵;再从新的距离矩阵中选出最小者dij,把Gi和Gj归并成新类,计算各类与新类的距离,直至各分类对象被归为一类[12]。利用SPSS软件对客观参量进行聚类分析,结果如图6所示。

图6 聚类分析结果
图6中横坐标为各类间距离。结合因子分析和聚类分析结果可将客观参量分为三类:第一类包含粗糙度、抖动度和尖锐度;第二类包含响度;第三类包含A计权声压级与语言清晰度。
4.3 相关性分析
将表2中主观偏好性试验值与表3中各客观参量进行Pearson相关性分析,结果如表5所示。相关性系数高于0.7时说明该客观参量与主观偏好值间具有较强相关[12]。
综合因子分析、聚类分析以及相关性分析结果可知,客观参量可分为三类,且各类中与主观偏好性相关系数最高的客观参量分别为响度(0.787)、尖锐度(-0.823)以及A计权声压级(0.863)。因此,提取该3个客观参量作为声品质偏好性建模及预测分析的客观参量。

表5 主观偏好值与客观参量的相关性系数
5 声品质预测模型的建立与检验
5.1 预测模型的建立
找出主观偏好性与客观参量间的影响关系是建立汽车关门声品质预测模型的关键。相关研究表明主客观参量间的关系实质为回归分析[13],因而本文采用支持向量回归机建立预测模型,回归问题拟合函数为
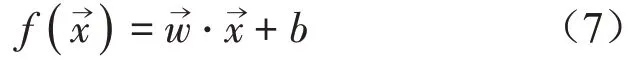
支持向量回归最优化问题数学表达式为
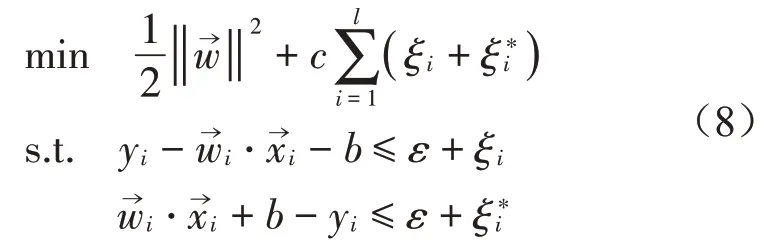
其中:c为惩罚因子,b为偏置;ξi和为松弛变量,且ξi≥0,≥0;ε为不敏感误差损失函数。引入拉格朗日乘子αi和以及核函数可得SVR的决策函数:

式中:且αi≠0,≠0;(x,xi)为训练样本集;K(x,xi)为核函数,本文选用适用性最广的高斯径向基核函数。
至此,建立了3个预测模型优化参数:惩罚因子c,径向基核函数中的σ以及损失函数中的ε。定义g=1/2σ2,p=ε,并引入遗传算法(Genetic Algorithm,GA)对SVR的决定参数进行寻优,该方法能高效寻求全局最优解[14]。
5.2 预测模型的检验
将主观偏好性试验分值与本文多元统计分析后提取出的客观参量响度、尖锐度和A计权声级代入GA-SVR模型中进行训练,得到如图7所示适应度线。
由图7可知,当种群进化到10代左右,最佳适应度值快速收敛并趋于稳定,训练后得到的最优参数为:c=104.792 8,g=2.894 4,p=0.016 506。将最优参数代入支持向量机即得一个初步预测模型,再将测试集代入初步模型验证模型精度,直至模型精度满足要求。
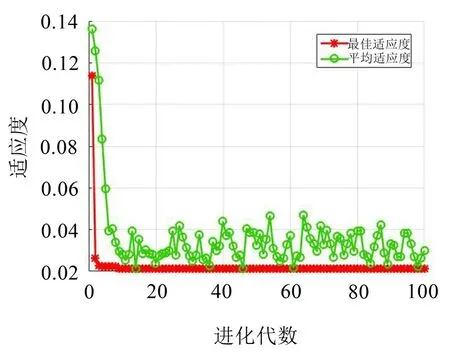
图7 适应度曲线图
由MATLAB可得最终模型结构体为

由模型结构体参数可知预测模型共有10个支持向量,则模型数学表达式为11项的和(包括常数项),表达式较为冗长复杂。此处以提取第一项决策函数为例,将模型结构体内参数代入式(9)、式(10),得到预测模型其中一项数学表达式为
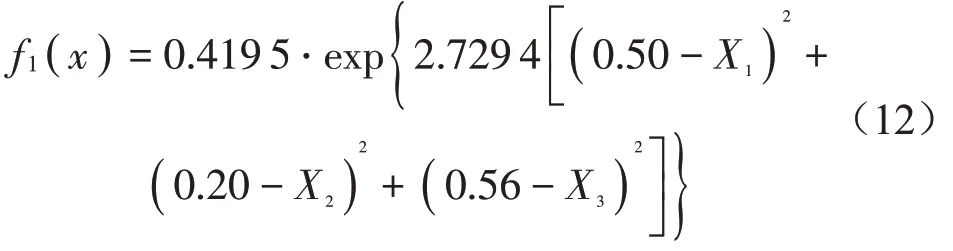
其中:x=(X1X2X3);X1——响度;X2——尖锐度;X3——A计权声压级。
由图8至图11及表6可知,对训练样本集和测试样本集,应用MSA-SVR模型得到的预测偏好性值与试验主观偏好性值的平方相关系数分别为R2=0.998 7和R2=0.972 9,均大于85%,高于未经多元统计分析时SVR模型的平方相关系数R2=0.948 3和R2=0.707 1,且预测均方误差mse都低于0.001,比未经多元统计分析SVR模型的预测均方误差mse值0.004 0和0.068 4要小很多,说明不管是从相关性系数还是从预测均方误差看,MSA-SVR模型预测偏好性值比无多元统计分析的SVR模型预测偏好性值更优。
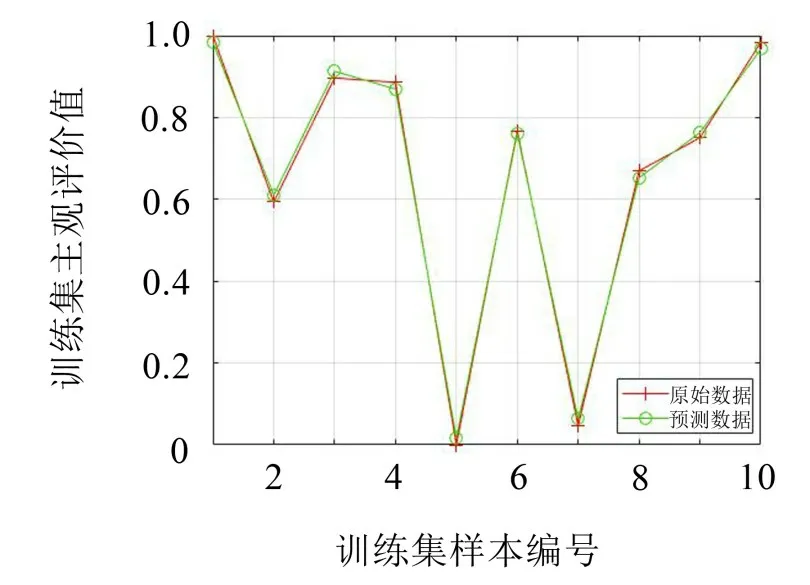
图8 MSA-SVR模型训练集样本预测结果对比
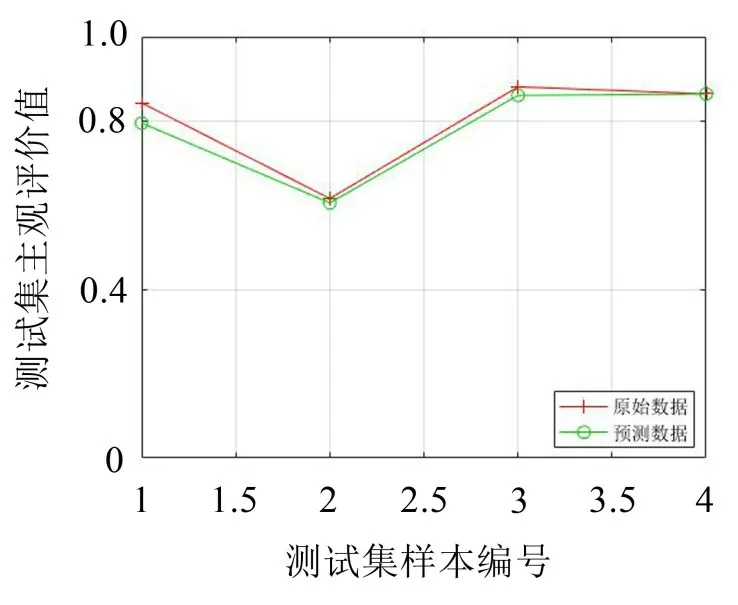
图9 MSA-SVR模型测试集样本预测结果对比

图10 SVR模型训练集样本预测结果对比
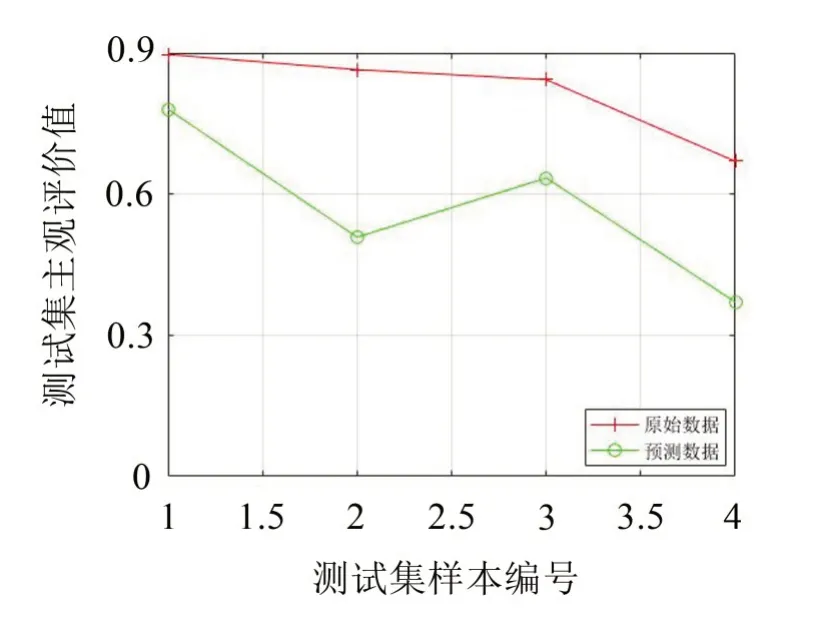
图11 SVR模型测试集样本预测结果对比

表6 预测模型预测结果对比
6 结语
计算得出了汽车关门声的主观偏好值及客观参量,通过因子分析与聚类分析找出各客观参量间相关性,并在此基础上,利用相关性分析得出主观偏好性与客观参量间的相关性系数,提取出了最能表征主观偏好性的客观参量:响度、尖锐度和A计权声压级。利用遗传算法对支持向量回归机主要参数进行寻优,得到了基于多元统计分析-支持向量回归的预测模型。MSA-SVR模型的主观偏好预测值与主观偏好试验值相关系数高于未经多元统计分析的SVR模型且其均方误差明显低于未经多元统计分析的SVR模型,说明MSA-SVR模型的预测能力显著提高,验证了多元统计-支持向量回归方法用于汽车关门声品质偏好性的预测是可行和高效的。
