局域共振型薄膜材料隔声机理与调控规律研究
2021-06-16张健周奇郑王德石高晟耀
张健,周奇郑,王德石,高晟耀
(1.海军工程大学,武汉 430033;2.92578部队,北京 100161)
隔声材料在航空航天、舰艇、环境噪声等领域有着广泛的应用。然而受质量作用定律[1]的影响,传统隔声材料在低频段的吸声效果不够理想,根据质量作用定律,低频段需要增加隔声材料的质量才能增强隔声效果,但增加质量与现有器械轻质重载的设计思路是相反的。而局域共振型薄膜材料的出现为研制新型的低频隔声材料提供了新的设计思路。局域共振型薄膜材料,是由薄膜上附加质量块并粘附在刚性框架上构成,该结构在声波激励下会产生局域共振,这类材料的隔声量相对质量作用定律预测的结果显著增加[2-4]。
Liu等[5]于2000年提出了声子晶体的局域共振带隙机理,通过将包覆软橡胶材料的大密度(铅球)质量块周期性地嵌入树脂基体材料中,形成了一种三维三组元复合材料,成功在小尺寸结构的条件下获得低频带隙。这种采用“软橡胶材料”附加“质量块”形式在振动控制领域通常用于实现动力吸振器结构[6],在声学领域实现共振单元也可以使用这一思路。Yang等[7]在2008年提出了薄膜型声学超材料的概念,并指出在低频段内,薄膜中心附加一个小的圆形质量块能够改善薄膜的声学特性,通过改变附加质量块的重量可以调整其有效隔声范围。之后,通过将具有不同有效隔声范围的声学超材料叠加在一起,增强了该结构的隔声性能。2010年,Naify等[8-9]通过阻抗管测试和有限元仿真研究了附加重量和薄膜张力对薄膜型声学超材料隔声性能的影响。Zhang等[10]创建了液体双共振单元结构,体积模量和质量密度在该结构中都为负值,之后通过建立声振分析模型,解释了反共振和共振引起的声波传输变化。2014年,Ma等[11]设计的薄膜型复合共振吸声的超材料,可以实现单个甚至多个频率的吸声。
目前对于局域共振板的振动已有许多研究[12],但是薄膜与薄板的振动有本质的区别,薄板中的恢复力来自于薄板的刚度,而薄膜的恢复力则来自于薄膜的张力。局域共振型薄膜材料通过薄膜和质量块的局域共振增强了结构对弹性波的吸收,从而提升隔声性能,并且材料的共振频率可以通过改变薄膜和质量块的结构参数来调整。此外,薄膜结构在空气中振动,其固有频率较低,阻尼较高,应当考虑薄膜结构声振耦合的分析。在隔声材料设计阶段,对局域共振薄膜结构进行声振耦合机理的分析,并且准确地评估薄膜材料的隔声性能非常重要。
本文采用解析法和有限元法相结合的方式对局域共振型薄膜材料的隔声特性进行预测,将两种方法的计算结果与实验进行对比,验证了模型和计算方法的有效性。通过分析局域共振薄膜材料模态振型与隔声性能之间的关系,发现当薄膜-质量块整体结构位移较大时,结构声辐射增强,隔声性能较差;薄膜-质量块反向振动,结构整体位移减小,两者结构声辐射相互抵消,隔声性能较好。此外,还详细研究了结构参数对于低频隔声性能的影响。
1 计算方法验证
1.1 薄膜-质量块声振耦合的解析解
为计算薄膜-质量块的隔声效果,本文以矩形薄膜附加质量块的结构为例,从膜的振动方程出发,得到了薄膜-质量块结构的声振耦合方程。
薄膜-质量块结构的尺寸和材料参数如下:薄膜张力为T,并且当薄膜振动时,该张力保持不变。薄膜的宽度、长度、单位面积面密度分别为a,b,ρs,质量块的宽度、长度、单位面积面密度分别为lx,ly,ρmass,在笛卡尔坐标系中,w(x,y,t)表示t时刻点(x,y)在z方向上的横向位移,图1为薄膜-质量块结构的示意图。

图1 薄膜表面附加质量
在方程推导过程中,忽略薄膜的抗弯刚度和质量块对薄膜振动的影响。由薄膜表面的力学平衡关系,可以得到薄膜的声振耦合方程为

式中:ρs,ρi,T别为薄膜的面密度、质量块的面密度和薄膜表面张力,pi,pr,pt分别为入射声压、反射声压和透射声压。入射声波为一列频率为ω的平面波,从z<0方向垂直入射到薄膜表面,表达式为
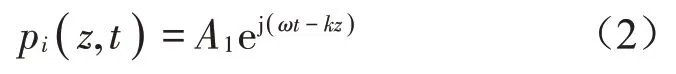
由声学边界条件可知,两种介质在分界面上的法向质点速度连续,即可得到总的声压作用力为
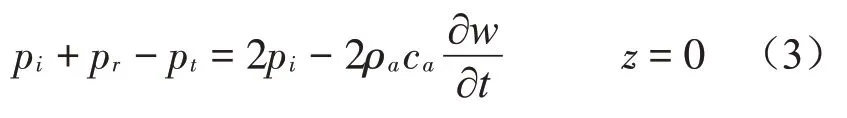
式中:k为波数,A1是入射声压幅值。ρa,ca分别为空气的密度和声速。ℏ(x,y,xi,yi,l xi,lyi)是Heaviside函数,表示4个阶跃函数的结合方程。

根据模态叠加原理,薄膜表面的振动位移可表示为

式中:km=mπ/a,kn=nπ/b。Wmn表示振动模态系数,sinkmxsinkny表示第(m,n)阶振动模态。
将公式(3)代入式(1),整理得到:

将式(5)代入式(6),方程两边同乘以ψpq=sinkpxsinkqy,并在整个膜结构表面进行积分(0≤x≤Lx,0≤y≤Ly),可以得到声振耦合方程如下:

式(7)可以写成矩阵形式:

式中:[W]表示振动模态系数,[M],[Q]分别代表薄膜、质量块的质量矩阵,[C]矩阵代表空气阻尼,[K]表示的是薄膜张力矩阵,而2A1[F]作为入射声波是整个结构的受迫振动的激励力。

由式(8)可知:

对于圆形薄膜的声振耦合分析则是在极坐标下进行,通常局域共振型薄膜材料的质量块都放置在圆形薄膜中心。与矩形薄膜类似,可以得到圆形薄膜的声振耦合方程。
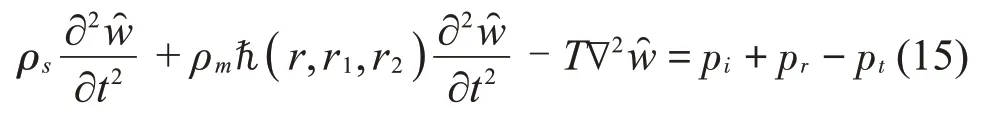
式中:ρm为质量块面密度,r1,r2分别为质量块的内、外半径,ℏ(r,r1,r2)是两个阶跃函数的结合方程,ℏ(r,r1,r2)=H(r-r1)-H(r-r2)。圆形薄膜的横向振动位移和各阶模态振型可表示为

式中:Jmn(kmnr)为贝塞尔函数,并且圆形薄膜的振动位移只与径向距离r相关,要求取m=0。各阶模态振型可简化为将式(15)两边同乘,即可对圆形薄膜的声振耦合方程进行化简,化简过程与矩形薄膜相同,此处不再赘述。
对于小尺寸膜结构,为简化计算,可使用膜结构表面平均振动速度表示透射声压:
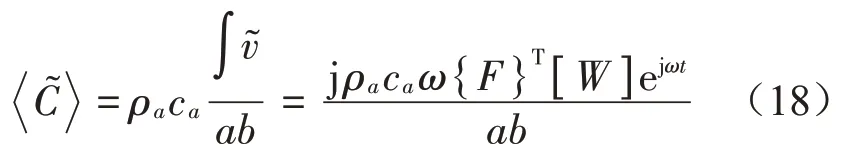
膜结构的声压透射系数可以通过透射声压和入射声压求得:
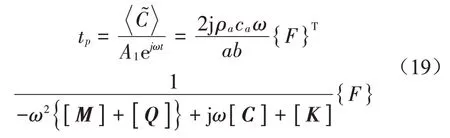
进而,可以得到局域共振型薄膜结构隔声量表达式:

1.2 有限元模型和计算方法
局域共振型薄膜材料是由弹性薄膜,质量块和刚性框架组成的复合结构,结构的配置方式对声学特性有很大影响,当采用复杂配置时,解析法难以有效处理,而有限元计算为此可以提供便利。
使用多物理场仿真分析软件COMSOL对薄膜-质量块结构进行有限元仿真。模型主要由薄膜-质量块结构单元和声场两部分构成,薄膜-质量块结构将声场分为入射声场和透射声场两个部分。为模拟低频噪声的声源特性,设置为平面波辐射,进入该边界条件的声波不存在反射情况。为了保证没有声波对外界透射,真实地模拟声场的入射及出射情况,四周边界设置为硬声场边界条件。将薄膜的四周设置为固定边界条件,在薄膜上施加x,y方向上的预应力。图2为仿真模型的示意图,在该模型下计算薄膜-质量块结构在声场激励下声波的传播损耗分布曲线。

图2 声场建模实体
1.3 计算结果分析验证
为验证解析法和有限元计算的有效性,将计算结果与Naify等的实验结果进行对比验证。其中材料的结构参数如下:薄膜的半径r=12 mm,厚度h=0.076 2 mm,预应力σx=σy=6.4×106Pa,张力T=σx×h,薄膜的质量密度ρ0=1200 kg/m3,薄膜面密度ρs=ρ0×h;附加质量块的半径r0=1.93 mm,厚度h1=5.2 mm,重量m=0.48 g,质量密度ρ1=7 870 kg/m3,质量面密度ρm=m/(πr02);声速c=340 m/s,密度为1.29 kg/m3。经过计算得到解析法、有限元法和实验结果的隔声量对比,如图3所示。
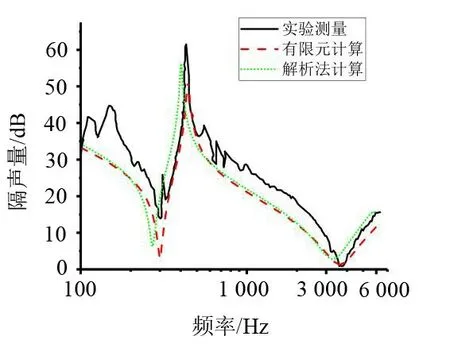
图3 隔声量
从图3可以看出,3种方法得到的结果变化趋势相同,都出现了一个隔声峰值和两个隔声谷值,实验测量对应的频率分别为427.9 Hz,301.4 Hz和3 679.3 Hz;与此对应的解析法计算结果为408.1 Hz,286.1 Hz,3 401.6 Hz;有限元仿真的结果为438.9 Hz,300.5 Hz,3 682.8 Hz。表1将解析法和有限元法与实验测量的数据相比较,对解析法和有限元法的精确度进行分析,括号内列出相对实验结果的精度误差。

表1 解析法和有限元法频率点的精确度/Hz
经过表1的对比,两种方法在低频时(第一隔声谷和第一隔声峰)的预测结果都较为准确,有限元法对于低频隔声特性预测的精度较高,随着频率增大,解析法的预测精度会逐渐降低。解析法预测误差较大的原因是因为忽略了质量块的弯曲刚度,质量块与薄膜接触的部分在实际振动时不会发生弯曲变形,从而导致了结果的误差。
在对结构的低频隔声性能进行预测时,解析法的计算时间很短,对几千个频率点的计算只需要几分钟的时间,并且物理意义明确,而有限元法的计算则相对繁琐,计算时间较长,参数设置不合理时容易导致结果不收敛;但是解析法只能针对简单小样品结构进行计算,有限元法则可以对复杂结构进行分析求解,可视化的后处理功能可以更直观的对局域共振型薄膜材料的声振特性进行分析。后文为了解薄膜-质量块结构的隔声机理,探究隔声机理与特征频率之间的关系,使用了有限元法对结构进行分析计算。
2 局域共振型薄膜材料声振耦合特性分析与优化设计
为找到局域共振型薄膜材料隔声机理的一般规律,首先对较简单结构进行了分析,以Naify等设计的结构为例,计算得到结构的前6阶特征频率,相对应的频率分别为296.8 Hz,687.7 Hz,689.7 Hz,827.1 Hz,2 951.6 Hz,3 552.5 Hz,发现第1阶与第6阶与薄膜-质量块的两个隔声谷相对应,其对应的模态振型如图4所示。

图4 与隔声谷相近的两个特征模态
图4(a)中质量块振动方向向上,带动周围的薄膜一起向同一个方向振动,这个振型是由质量块和其周围薄膜组成的“重物-弹簧”系统共振引起,变形较大,从而导致结构声辐射能量增强,隔声性能较差。图4(b)的振动可以看作质量块以及框架连接处薄膜无振动,剩余部分薄膜振动时产生的振型,因为薄膜发生了巨大的形变,也导致隔声能力减弱。隔声峰位于这两个特征频率之间,隔声峰频率点处的整体振幅如图5所示。

图5 隔声峰处的结构振幅
图5中隔声峰处结构振幅是第1阶和第6阶特征频率的叠加,即在这2阶特征频率之间,会出现一个频率点,使质量块与周围薄膜一起振动,并且振动方向相反,结构的整体位移减小,隔声性能增强。
薄膜中心附加一个质量块的结构,相对于传统隔声材料的隔声性能明显提高,然而其对于亚波长的隔声能力有限,为提高局域共振型薄膜材料的低频隔声性能,拓宽结构的亚波长隔声频带,设计了一种矩形薄膜上附加对称半圆形质量块的结构,并对其低频隔声性能进行分析。该结构由长度30 mm,宽度15 mm,厚度0.2 mm的弹性薄膜,两片半径为6 mm,厚度为1 mm的半圆形铁片构成,并且两块铁片对称放置于y轴的两侧,为了与Naify等的结构区分,并方便下文描述,将薄膜上附加对称半圆形质量块的结构称为结构A。
薄膜材料为硅橡胶,其杨氏模量和泊松比是美国的Damping Technologies公司利用夹层梁配置法测量:分别测量两块钢板之间有膜和无膜时系统动力学性质的变化而得到。杨氏模量实部的测量结果最终取100 Hz~1 000 Hz频率范围内杨氏模量的平均值:

杨氏模量虚部通过拟合实验吸收谱得到:
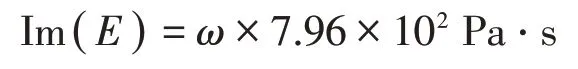
最终测得的杨氏模量为
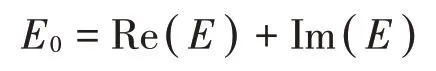
弹性波在材料中传播时存在损耗,所以在有限元计算中应该考虑杨氏模量的虚部。ω是角频率,质量密度为980 kg/m3,泊松比为0.3。薄膜上下为空气域,气压为一个标准大气压。薄膜初始应力为σx=σy=2.2×105Pa。质量块的密度、泊松比和杨氏模量分别是7 870 kg/m3、0.3、2×1011Pa。对上面的有限元模型进行计算,可以得到图6所示的隔声量变化曲线。

图6 局域共振型薄膜材料隔声量变化曲线
从图6可以看出,该材料在200 Hz~750 Hz的低频段隔声性能较强。两个隔声谷的频率f1,f3对应的频率为194.6 Hz,745.2 Hz;隔声峰值对应的频率f2为284.7 Hz。通过有限元软件计算得到薄膜材料在四边约束下的特征频率和其对应的模态振型。发现有两个特征频率与隔声曲线的两个隔声谷频率相近,分别为195.41 Hz、747.16 Hz,对应的模态振型如图7所示。

图7 结构A隔声谷的模态振型
图7(a)的变形集中在两个质量块上,质量块同时向z方向振动,带动两个质量块中间的薄膜也发生较大变形;图7(b)的振动主要集中在中心薄膜上,质量块处几乎无位移,薄膜隔声峰处的结构振幅如图8所示。

图8 结构A隔声峰处的结构振幅
隔声峰处的结构振幅表现为质量块与薄膜振动的叠加,质量块向内“翻转”,中心处薄膜向z轴负方向振动。为了更直观地分析结构振动对于隔声性能的影响,将两处隔声谷以及隔声峰处沿薄膜表面对角线的横向振动位移剖面函数画出,如图9所示。

图9 结构A隔声谷、隔声峰处的结构振幅
通过图9可以更直观地看出两处隔声谷的整体结构位移较大,产生了较强的结构声辐射,隔声性能降低。隔声峰处的结构振幅是两处隔声谷振幅的叠加,两侧质量块呈现向上“扇动”的形态,中心处薄膜向下振动,整体结构位移较小,两者产生的结构声辐射相互抵消,整个结构形成了一个开放的共振腔,使得隔声性能增强。
将结构A与前文薄膜中心附加一个质量块结构的声振特性相对比,两者的第一隔声谷频率分别为194.6 Hz,300.5 Hz;隔声量大于15 dB的隔声频段分别为240 Hz~460 Hz,330 Hz~1 600 Hz,结构A对于亚波长的隔声能力明显提升。通过对两种结构的模态振型进行分析,发现局域共振型薄膜材料第一隔声谷的产生受质量块的影响较大;而第二隔声谷的产生则更加依赖于薄膜;隔声峰则是由于质量块与其附近薄膜振动反向时产生。
3 局域共振型薄膜材料结构参数的设计
为获得薄膜与质量块对局域共振型薄膜材料隔声性能影响的规律,对薄膜上附加对称半圆形质量块结构的薄膜厚度,质量块厚度、摆放位置,预应力等几个因素对低频隔声性能的影响进行了分析计算,并列表说明结构参数对第一隔声峰的影响,计算结果如图10所示。
如图10(a)和表2所示,随着薄膜厚度增大,隔声量的第一隔声峰逐渐减小,所对应的频率逐渐增大。厚度增加5倍,隔声峰向高频移动了282.43 Hz,隔声量下降了8.45 dB,薄膜厚度增大,张力随之增加,低频激励下隔声量下降。
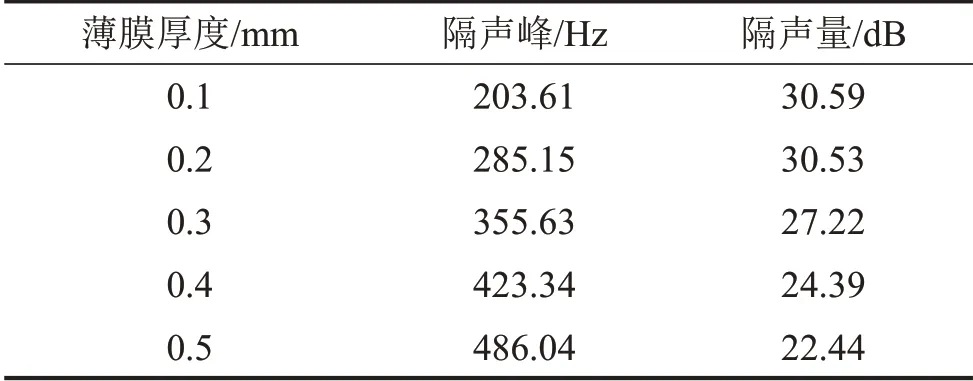
表2 薄膜厚度变化对第一隔声峰的影响
图10(b)和表3表明,质量块之间的距离减小,局域共振型薄膜材料在声波激励下形成的“共振腔”弹性波吸收能力变弱,第一隔声峰峰值降低,所对应的频率增大。质量块之间距离8 mm,隔声峰频率向高频移动了26.28 Hz,隔声量降低5.01 dB。通过图10(c)和表4发现质量块厚度从0.1 mm增至1 mm,隔声峰向低频移动了386.73 Hz,隔声量增大了28.81 dB;厚度从1 mm增至2 mm,隔声峰向低频移动了90.04 Hz,隔声量增加了0.83 dB,隔声峰向低频移动和隔声量增长的幅度减小很大。由前文模态分析可知质量块对第一隔声谷的影响较大,厚度增加即对应质量面密度变大,增强了低频段薄膜和质量块的共振,导致隔声量逐渐增大。但隔声量的增长幅度在质量块厚度达到1 mm之后会明显减小。图10(d)和表5所示,随着预应力增加,隔声曲线整体向高频移动,隔声峰也逐渐增大,并不利于材料的低频隔声。预应力增加,即是增加了薄膜的张力,薄膜在共振时的恢复力增强。

表3 质量块位置变化对第一隔声峰的影响

表4 质量块厚度对第一隔声峰的影响
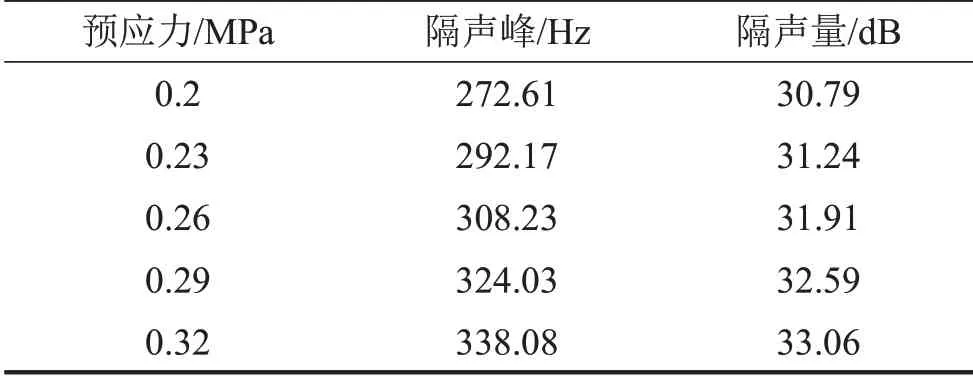
表5 预应力变化对第一隔声峰的影响
局域共振型薄膜材料打破了质量作用定律的限制,通过薄膜与质量块的共振实现了轻质材料高效率的低频隔声性能。通过以上分析,针对低频隔声需求,可以通过减小薄膜厚度和预应力,适当增加质量块之间的距离和质量块的厚度来实现。
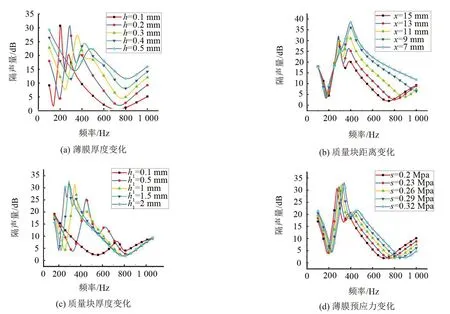
图10 结构参数变化对隔声性能的影响
4 结语
本文将解析计算、有限元分析和实验结果相对比验证了计算方法的有效性。然后使用有限元法对局域共振型薄膜材料的模态振型与隔声性能之间的关系进行了分析,并设计了薄膜上附加对称半圆形的机构,提高了结构的亚波长隔声性能,此外,还分析了结构参数对于隔声性能的影响规律。
研究结果表明:
(1)局域共振型薄膜材料具有较强的低频隔声性能,薄膜上附加对称半圆形质量块的结构亚波长隔声性能较强,隔声峰值频率为284.7 Hz,隔声频段位于240 Hz~460 Hz。
(2)局域共振型薄膜材料的第一隔声谷的共振频率受质量块影响较大;第二隔声谷的共振频率则主要依赖于薄膜;隔声峰处质量块与薄膜的振动反向,两者产生的结构声辐射相互抵消,隔声性能增强。
(3)对于薄膜上附加对称半圆形质量块的结构,薄膜厚度和预应力减小,薄膜张力随之减小,导致结构的低频隔声性能增加;增加质量块厚度的方式增强低频隔声性能,但是质量块厚度超过1 mm后,增长幅度有限;质量块之间距离增大,并且相隔13 mm时,低频隔声性能最好。
研究结论可以针对实际工程需要,为局域共振型薄膜材料的设计提供理论依据。
