A计权电路对p－p声强法测量精度的影响

陈 品， 陈心昭

（合肥工业大学机械与汽车工程学院，安徽合肥 230009）

瞬时声强是测点处声压和质点速度的瞬时矢量乘积［1］。根据质点速度获取方式的不同，声强测量方法通常分为2种，即使用传声器和质点速度传感器直接进行测量的p－u法［2］和通过双传声器测量声压梯度间接获得质点速度的p－p法［1］。基于p－p法的测试系统更易于实现，故目前较多采用。

声学测试使用的电容式传声器在有效频带内的幅值特性较为平坦，若要体现人耳对声音的感受，须对信号进行A计权处理。使用数字方式进行频率计权，通常可以达到较好的计权精度［3］，但仍存在2个难以解决的困难：① 电容式传感器对低频振动和扰动声较为敏感［4］，这使得量程设置较小时信号很容易饱和，A声级测试的上限不能很高，此时受ADC有效分辨率的限制，数字式A计权声级动态测量范围也较小；② 数字计权运算需要足量的原始时域信号，为保证测量的实时性与精度，系统对硬件提出了较高要求。数字计权通常采用FFT和IIR数字滤波2种方法。前者对运算速度要求较高，需要较多内存；后者对运算精度要求较高，字长效应较为明显［5］。

比较而言，使用模拟电路完成信号A计权处理，是一种较为经济且不增加系统负担的设计方案。但需要注意，A计权电路阻容网络中元件的电气特性漂移和匹配性变化都会对电路幅频特性和通道间相位匹配性产生影响，这些因素将会一定程度地影响声强测量的精度。

1 A计权电路参数计算

A计权由混合的高低通滤波电路实现，为尽可能减少电路中运放的个数，前级为一个带通C计权阻容网络，后级为一个无反馈高阻尼的二阶高通阻容网络，如图1所示。

图1 实现A计权的混合滤波电路

将C计权电路改为导纳标记，根据节点电压法，各节点的方程为：

其中，Vd＝V0／Af＝V0；Af＝1。

各元件导纳为：

联立方程组，整理得C计权电路传递函数：

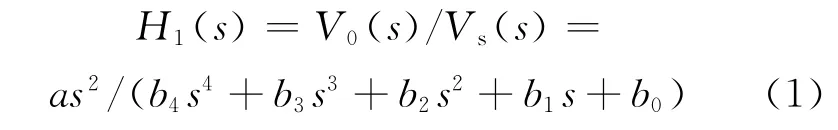
其中

同样计算后级二阶高通电路传递函数为：

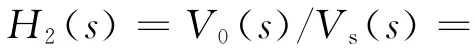
其中

则A计权电路的传递函数为：

为便于元件筛选，令R1＝R2＝R12，R3＝R4＝R34，R5＝R6＝R56，C1＝C2＝C12，C3＝C4＝C34，C5＝C6＝C56，以倍频程A计权标称衰减率［6］为基准，对（3）式做幅值最小二乘法优化计算，确定电路参数。电阻在精密级电阻值中选择，电容圆整为标称值，计算结果见表1所列。

表1 A计权阻容网络元器件计算参数

2 A计权电路引入的声强误差分析

2.1 p－p声强计算方法的固有误差

p－p声强法使用声压梯度近似计算质点速度，使得该测量方法存在固有系统误差。对于平面简谐声场p＝paej（ωt－kx），其无功声强为0，复声强［1，7］为：

（4）式中的系数是平面波声强I的真值，（5）式为p－p声强法的固有系统误差［8］：

2.2 A计权幅值误差分析

声强计算所需的声压信号是通过常规声学测试获得的，由（4）式系数可以看出，A计权电路幅值误差直接影响到声强计算精度。

A计权理论公式为：

其中，A1000＝－2.0 d B，f1＝20.6 Hz，f2＝ 107.7 Hz，f3＝737.9 Hz，f4＝12 194 Hz。

将表1的阻容圆整值带入（3）式，与（6）式比较后得A计权电路幅频误差曲线，如图2a所示。在声强常规测试频带63 Hz至6.3 k Hz内观察，幅值误差小于0.07 dB。

频域数字线性修正后的幅值误差如图2b所示，误差值进一步降低至0.004 dB。电路阻容值的圆整为幅值差产生的主要原因。文献［9］规定，Ⅰ级声强仪在100～4 000 Hz内计权误差不超过±0.5 dB，此频率范围外的计权允差≥±0.75 dB。可见圆整参数后，获得的A计权电路幅值精度是很高的。

受时间、温度和湿度等环境因素的影响，计权电路中各元件参数会发生漂移。选用精密级金膜电阻，可将阻值漂移变化量控制到极低。相比之下，电容更易受到环境温度影响，温度系数通常为300 mmp／℃左右，设工作温度为（20±30）℃，则C12、C34、C56容值在恶劣条件下的变化率K约为±1%。该条件下计算得A计权电路幅值误差曲线，如图3所示。

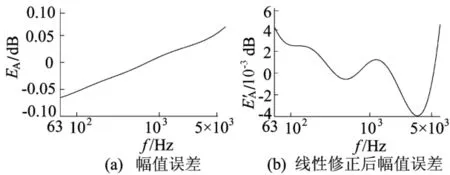
图2 计权电路圆整参数后的幅值误差

图3 环境温度对计权电路幅频误差曲线的影响

与C12、C34相比，C56漂移对计权电路幅频误差影响最大，在63 Hz处可达±0.15 dB，此值仍远低于文献［9］在该频率处计权误差要求。

改善电路运行环境、选用性能稳定的电容器，或使用频域修正等方法均可有效降低A计权电路引入的幅值误差。由于C12和C56的误差曲线相似，元件选择时使其温度系数符号相反，可一定程度抵消误差。对电路中容值相同的2个电容器，分别选择温度系数符号相反的材料类型也能很好地降低幅值误差。

2.3 相位失配误差分析及电路参数调整

由于电容高精密级测试较为困难，且电路中存在一定寄生电容，电容元器件即使经过筛选也很难做到各通道间高精度匹配，由此产生的A计权电路通道间相位差也将影响到声强测量精度［7－12］。

设筛选时通道间电容值失配率（容值的相对误差）K控制为±1%，对（3）式两边分别求C12、C34、C56偏导，带入（5）式，计算得相位差和对应的声强测量误差，如图4～图6所示。双传声器间隔棒分别取50 mm和12 mm，关注的频率范围分别为63～1 250 Hz、250～5 000 Hz［10］。

比较后不难看出，C34容值失配对声强计算精度影响很小，C12和C56的容值失配会增加低频处声强计算的误差。C56的失配误差影响最为显著，在63 Hz、250 Hz处最高可达0.35 dB和 0.5 d B。此外可以看到，C12、C34、C56失配产生的声强误差随着频率或隔离棒距离的增加而呈现降低趋势。由于筛选时很难实现电容值高精度的匹配，因此在为声强仪配置A计权电路时，可通过微调C12和C56相应电阻R1、R2、R5、R6对其进行补偿，达到降低模块间相位差的目的。观察图4a、图5a、图6a发现，C56误差在100～700 Hz间相位差较大，且曲线较为平坦；而在这频率区间内C12和C34相位差的绝对值总和在500 Hz左右最小（约0.8°），即当各电容失配率相同时，通道间在500 Hz处的相位差主要由C56产生，故建立电阻调整策略。先微调R5、R6使得双通道整个计权电路在500 Hz处相位差降至最低，之后微调R1、R2，使得双通道相位差在20 Hz低频处降至最低。试验表明这种调整方法行之有效，相位误差可降低至未调整时的1／5左右。

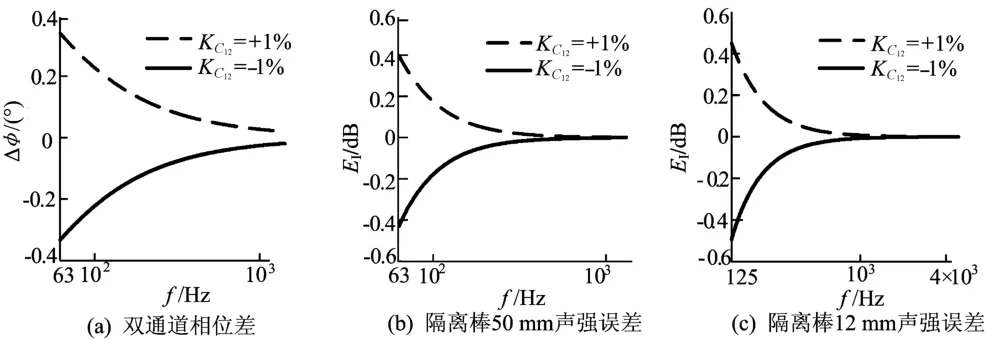
图4 计权电路C12失配引入的相位失配与声强误差

图5 计权电路C34失配引入的相位失配与声强误差

图6 计权电路C56失配引入的相位失配与声强误差

2.4 A计权电路引入的声强测量不确定度评定

为更全面、准确评估A计权电路对声强测量精度的影响，对其进行不确定度评定。

A类不确定度通过统计方法计算不确定度分量［12］。测试时使用信号发生器，在频率63 Hz和 250 Hz处发出2路相位差为λd的简谐波模拟自由声场，λ为该频率点波数，d分别取50 mm和12 mm。计权电路后端直接接入互谱信号分析仪，计算声强级频率响应的偏差。任意选取10组A计权电路，实测结果见表2所列。

表2 63 Hz（50 mm）、250 Hz（12 mm）A计权电路A类不确定度评定 dB

由表2可得：

其中，uA，f为测试频率f下A类标准不确定度。由于测试样本数n≥10，故安全因子h取1。

电容偏差和电容失配引入的声强测误差是A计权电路B类不确定度的主要来源，各不确定度分量可由误差极限值和置信因子获得，其相互之间的关系为：

其中，αi为xi的误差极限值；ki为置信因子，服从均匀分布，取。

由图3～图6的计算数值可得各误差源引起的B类不确定度分量，见表3、表4所列。

表3 63 Hz（50 mm）A计权电路B类不确定度评定 dB

表4 250 Hz（12 mm）A计权电路B类不确定度评定 dB

由于各误差源相互无关，整个电路对声强测量的B类不确定度分量可由（8）式计算：

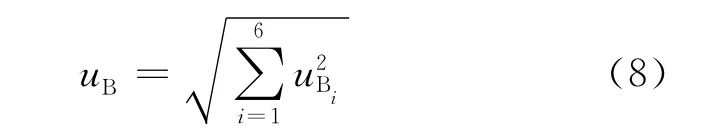
50 mm和12 mm下限频率63 Hz和250 Hz处的声强测量B类不确定度分别为：

uB，63Hz＝0.319 dB， uB，250Hz＝0.298 dB，带入合成标准不确定度（9）式：

得uc，63Hz＝0.322 dB，uc，250Hz＝0.304 dB。

计算后可以看到，低频处合成的标准不确定度均低于文献［9］规定的Ⅰ级声强仪计权频响允差范围，即±0.75 d B和±0.50 d B，故模拟A计权电路完全可以满足精密级声强测量的要求。

3 结束语

本文推导的A计权模拟电路传递函数公式圆整参数后，电路在幅值上对声强引入的误差小于0.005 d B，若考虑环境因素影响（－10～50℃电容最大产生±1%飘移），幅值总误差可控制在0.2 d B以内。元器件筛选时若能保证容值失配率小于1%，则A计权电路声强级测量的合成标准不确定度满足文献［9］允差要求。若要达到更高级别的声强测试精度，需按照电阻调整策略对电路进行微调补偿。此外增大隔离棒距离，提高有效测试频率的下限，也有助于降低A计权电路对声强测量精度的影响。

［1］ 蒋孝熠，连小珉.声强技术及其在汽车工程中的应用［M］.北京：清华大学出版社，2010：48－50.

［2］ 何元安，贾志富.P－U法声强测量及其应用研究［J］.声学技术，1999，18（A11）：195－196.

［3］ 何岭松.频率计权网络的公式化表达［J］.仪器仪表学报，1996，17（5）：540－542.

［4］ 白 川.传声器的振动噪声及其降低方法［J］.电声技术，1984（2）：44－49.

［5］ 金 晖，何 洁.频率计权的全数字实现［J］.仪器仪表学报，2006，27（6）：1495－1496.

［6］ GB 3785－1983，声级计的电、声性能及测试方法［S］.

［7］ 周广林，陈 剑，毕传兴，等.双传声器声强测量系统误差分析与不确定评定［J］.农机学报，2003，34（5）：126－128.

［8］ Gade S，Sc M.Technical review－Sound intensity（Part 1）－No.3［M］.Denmark B＆K，1982：20－21.

［9］ JJG 992－2004，声强测量仪检定规程［S］.

［10］ Jacobsen F.A sound intensity probe for measuring from 50 Hz to 10 k Hz［M］.Denmark B＆K，1996：3－7.

［11］ 罗 刚.不确定度A类评定及不确定度B类评定的探讨［J］.计量与测试技术，2007，34（12）：42－43.

［12］ 陈心昭，毕传兴，李卫兵，等.基于分布源边界点法的新型近场声全息技术［J］.合肥工业大学学报：自然科学版，2005，28（9）：961－966.