纸纱复合袋糊底机羊角展开装置的振动分析

2021-06-16翟鹏彭珍瑞胡明扬

噪声与振动控制 2021年3期

翟鹏，彭珍瑞，胡明扬

（兰州交通大学机电工程学院，兰州 730070）

纸纱复合袋糊底机是一种用于制作纸纱复合袋的机器，其主要的功能是将制袋机生产出的袋筒两端糊底。糊底工艺流程为将制袋机制作出的袋筒依次经过吸开、展平、压痕、涂胶、贴阀、折边成型[1]。其中展平工序是通过羊角展开装置将纸袋展开铺平在工作面板上。但是在该工序中，由于展开装置杆件之间的连接方式为铰接，铰接处存在一定的间隙导致展开臂的运动精度降低、运行不平稳，会对零部件形成一定的冲击。另外装置本身也会产生较大的振动，对展开臂的运行造成一定程度的影响，会降低装置工作的稳定性，缩短其使用寿命。

许多学者对此方面进行了研究。刘福才等[2]将空间机械臂作为对象，研究了运动副间隙对机构系统动态特性的影响。娄军强等[3]对机构的运动轨迹进行规划，降低振动，王建强等[4]发现振动传递特性对于发动机的减隔振安装设计有重要作用，Li等[5]利用输入振型和自适应参数自抗扰控制器对柔性关节机械臂的振动进行主动控制。以上是对机械臂进行抑振研究的方法，但是对于铰接类杆件的抑振研究较少，并且都未曾应用到包装设备中。而张发军等[6]通过调整杆件的质量分布抑制振动，其主要适用于铰接杆的铰接处由于间隙造成振动的情况，因此该方法对于解决机械臂在工程应用中产生振动的问题，具有积极的意义。

本研究主要是为了解决纸纱复合袋糊底机展开臂因振动较大造成的稳定性差、运行不平稳、精准度不高等工程问题。结合铰接杆的特性,通过分析展开臂的动力学模型，对展开臂装置进行抑振优化。首先对展开臂进行受力分析，建立动力学模型，然后利用ANSYS软件进行模态分析，接着在振型计算的测点处布置传感器，测量不同材质不同重量分布时杆件的加速度信号，对比分析结果后确定最优方案，从而达到抑制展开装置振动的目的，由此来减少由于振动较大造成的消极影响。

1 展开装置结构及工作原理

根据工艺流程和工作空间的要求，设计了一套展开装置，如图1所示。主要由支架、链轮（2个）、侧板（2个）、连接杆（2个）、展开杆（2个）、万向节（2个）、工作面板等部分组成。展开装置的杆件连接方式均为铰接。左右两侧的连接杆、展开杆、万向节组成了两套展开臂。各组成部分功能为：动力输入通过链轮和链条带动机构转动，侧板提供工作角度，保证展开杆能够很好的展开纸袋，展开杆由连接杆连接，保证同步转动，展开杆在工作时既能展开纸袋，也能对纸袋的尾部起到抚平的作用。

图1 展开装置实物图

工作原理：纸袋在经过前面的工序处理后，运动到展开装置处，此时纸袋中间形成一条缝隙，展开杆顺缝隙进入，展开杆的转动和向前进给的运动同步工作，在展开臂的作用下，将纸袋展开平铺在工作平台上。

在SolidWorks中绘制展开装置的模型，如图2所示。装置长468 mm，宽1 068 mm，高356 mm，装置固定在工作平台上，展开杆的圆弧半径290 mm，杆的直径8 mm，中间连接杆长180 mm，展开杆的材料为45号钢，其他所有位置的材料均为铸铁，铸铁泊松比为0.25，密度为7 100 kg/m3，弹性模量为1.5×1011Pa。

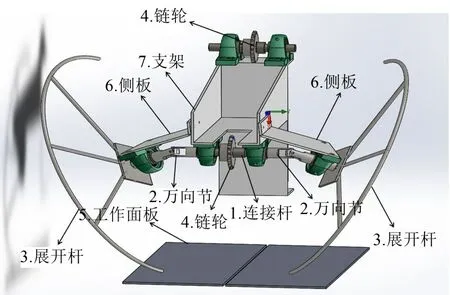
图2 展开装置模型

2 展开臂动力学建模

由于展开臂的杆件连接方式均为铰接，导致杆件的关节处存在偏心，即展开臂关节处连杆的轴颈轴心与连杆的轴套轴心不重合，造成x和y方向均存在偏心量enx和eny[7（]n=1,2,3,4,…）。由此可知，展开臂每个关节处的间隙会使得整个装置有2个自由度的增加。考虑到装置结构对称，所以此处仅以左侧展开臂为研究对象，其等效示意图如图3所示，其中1为连接杆，是驱动杆。展开臂的自由度为7。

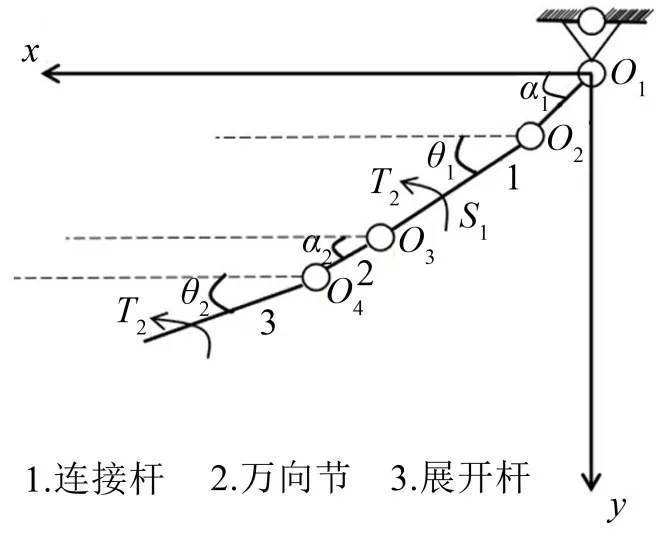
图3 展开臂结构等效示意图

由图3中可知，几何关系如下：

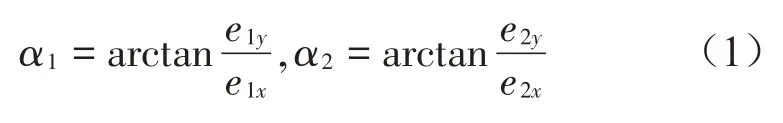
因此在展开装置运行过程中，连接杆1质心s1位置坐标方程为

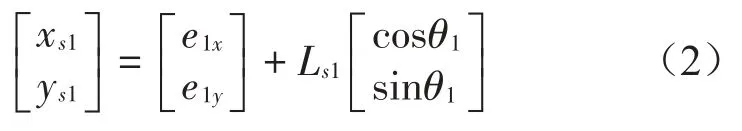
将式（2）求导，可以得到连接杆质心s1的线速度为

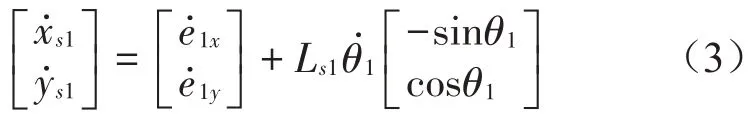
再将式（3）求导，便可以得到连接杆质心s1加速度方程：

对连接杆1受力分析如图4所示。图中，因为铰接关节处存在间隙，所以关节与连接杆、展开杆在运动时会产生碰撞。

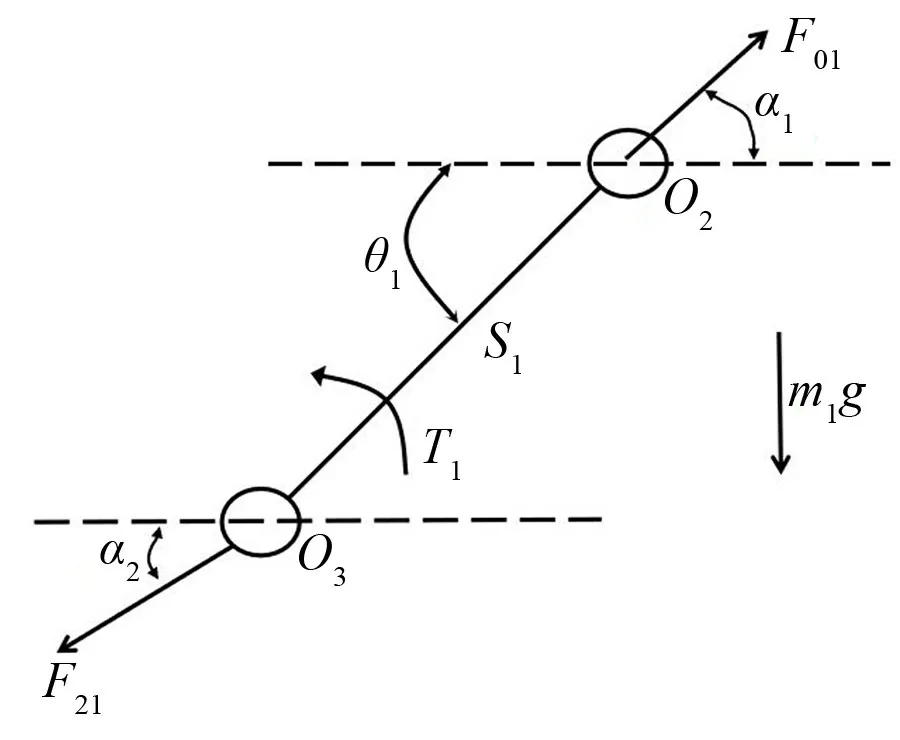
图4 连接杆受力分析

根据达朗贝尔原理，可得：

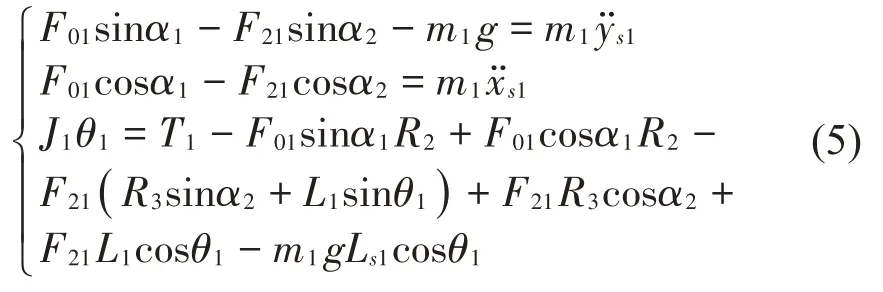
式中：F01为连接杆于基座之间的碰撞力，F21为展开杆即连杆2对连接杆之间的碰撞力。

同样地对展开杆，即连杆2分析可知：

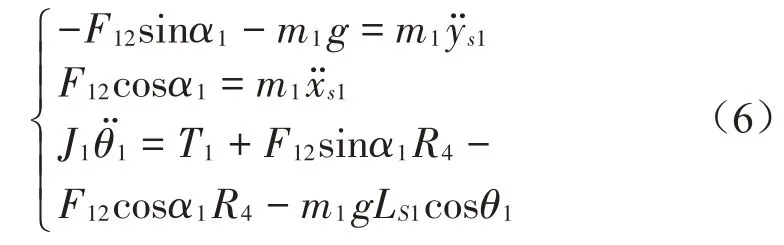
式中：T1为连接杆所受扭矩，F21为展开杆对连接杆之间的碰撞力，F12为连接杆对展开杆的碰撞力，其中F21和F12为相互作用力；R3分别为连接杆的关节处轴套半径，R2和R4分别为连接杆和展开杆的关节处轴颈的半径；J1和J2为连接杆和展开杆的转动惯量。

将式（5）和其求导后的式（6）整理后便可以得到展开装置动力学模型：

3 模态分析及试验测点选择

由以上分析可知，展开臂由于其构成为含间隙的铰接杆，而铰接杆特性造成了装置的振动较大，需要通过优化设计方案，来降低展开臂的振动[8]。为了得到有效的试验数据，需要对展开装置进行模态分析，根据其振型优选测点。

3.1 模态分析

实际工作时，考虑到两边的展开杆没有振动产生的损伤，并且在试验时，传感器不便安装，所以在模态分析时，暂时将两杆去除，变成如图5所示的模型进行模态分析。将模型导入ANSYS软件中，将模型整体进行网格划分，由此得到24 955个节点和12 746个单元，通过分析，前4阶模态可以很好地计算所需振型数据，因此计算其前4阶的模态，提取振型矩阵进行分析来选择测点，前4阶模态如图6所示。由模态图中可以看出，模型两侧的侧板以及支架前端处容易出现弯曲变形，导致装置在运行时产生振动变形，甚至出现损伤。

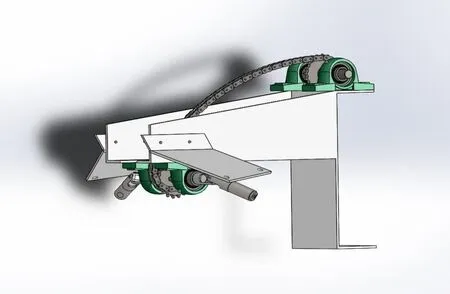
图5 模态分析模型

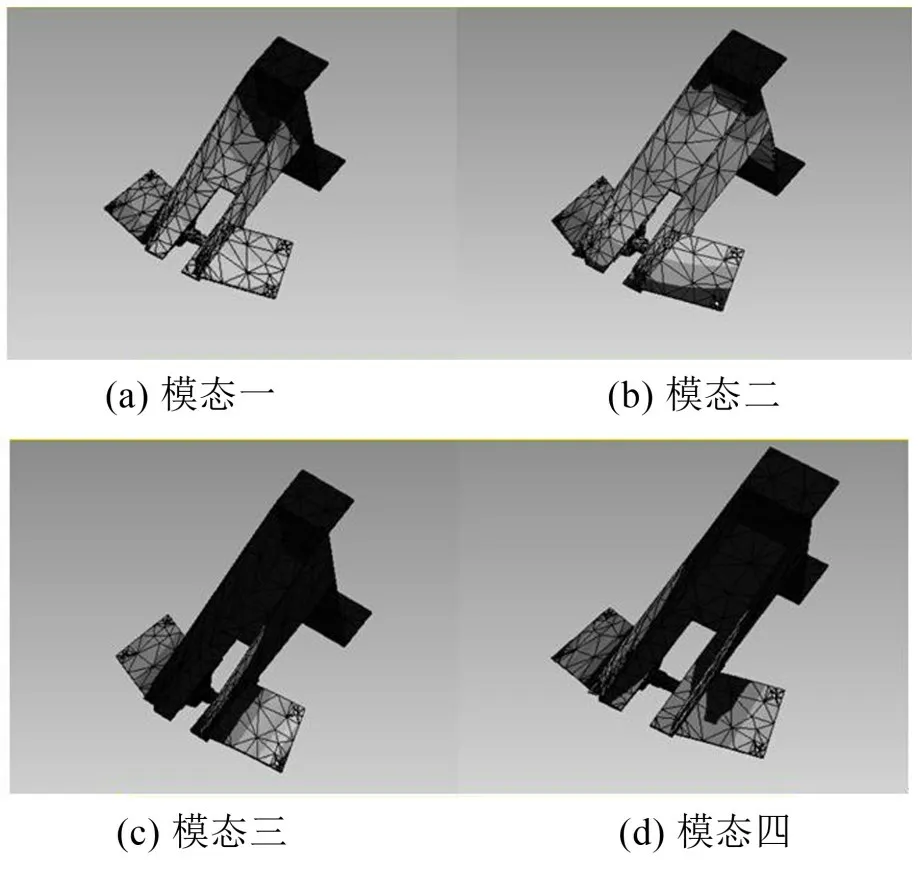
图6 展开装置的4阶模态

3.2 测点选择

由于周围环境的振动、噪声以及装置本身复杂结构会对试验结果造成影响，难以获取准确的信息，因此需要优化测点，获取展开装置较为准确的振幅、频率等信号。本文选择有效独立-平均加速度幅值法来选择最佳测点[9]，一方面有效独立法仅考虑测试自由度对截断模态秩的贡献，使测试自由度比平均加速度幅值小[10]。另一方面仅让布置的最佳测点平均加速度幅值较大，会导致测试模态之间的线性独立性变差。因此需要结合两者的优点来布置测点，如式（8）所示，它既结合了平均加速度幅值法，使得布置的最佳测点平均加速度幅值较大，又结合了有效独立法，使得测试模态尽可能的线性独立[11-12]，保证传感器布设在结构响应的幅值点。

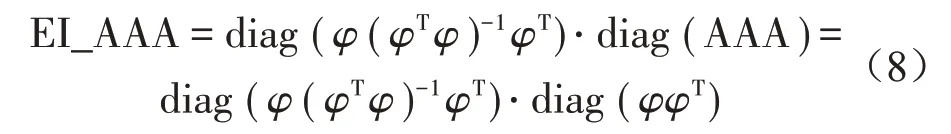
提取前4阶模态振型数据，在MATLAB中用EIAAA法得到5个测点，测点位置如表1所示。在实际装置中的节点对应测点的位置如图7所示，且所得传感器布置方案实际可行。

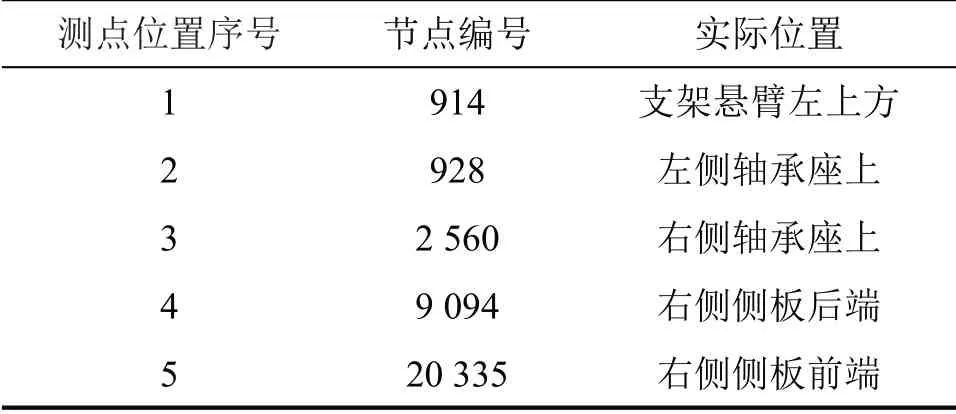
表1 测点位置

图7 测点位置

4 展开臂试验及结果分析

试验采样时间为10 s，根据香农采样原理并结合试验经验可知采样频率为3 kHz，传感器使用INV982X系列的ICP型压电式加速度传感器，采集仪使用INV3062-C2(L)型采集仪，试验测量展开装置垂直方向上的加速度数据。因为测得的信号受环境噪声干扰的影响，所以对试验信号采用非局部均值法进行降噪处理。

非局部均值降噪（NLM）基本思想是对测试信号中相似的部分进行加权平均来消除噪声[13]。在机械振动信号中，NLM通过对原始信号的恢复，将叠加在振动信号上的噪声去除，从而达到较好的降噪效果[14-15]。本文采用NLM方法对加速度信号进行降噪处理，提高加速度信号的信噪比，提取微弱特征频率信息。

4.1 改变不同质量分布前测试试验

展开装置主要干扰来源是机器本身的振动和环境噪声的干扰。在试验的10 s内展开装置运行了7.5个周期，共进行了6次试验，5个传感器共测量得到30组数据。

对比分析5个位置测点的信噪比和均方差，如表2所示。位置3处的信噪比最大，均方差最小，如图8所示。从实际测量来看，位置3也是较好的位置。因此选取位置3即节点编号为2 560的时域信号。

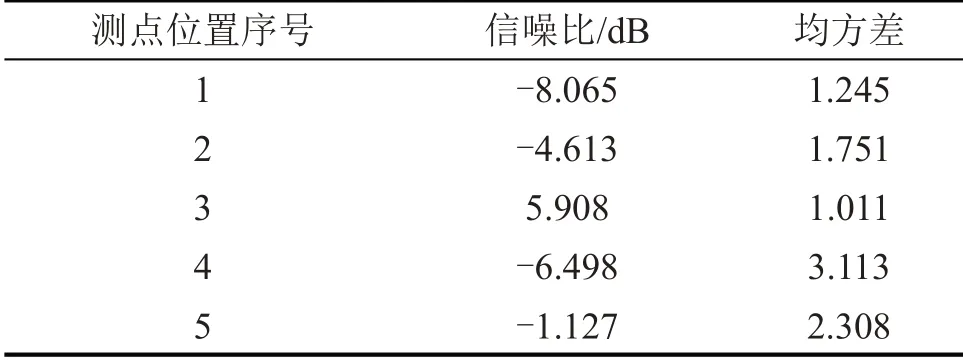
表2 5个测点位置信噪比及均方差对比

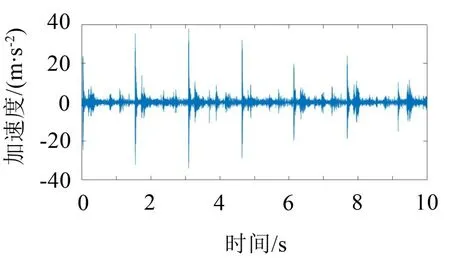
图8 降噪前时域波形图

经过NLM降噪处理后，得到如图9所示的时域波形图。用加速度幅值、峰值因子和峭度3个标准来衡量减振效果。加速度幅值表示加速度的最大值，越小越好；峰值因子表示装置所受冲击，越小越好；峭度表示装置所受振动大小，越小越好。通过对时域信号的分析，可以得知展开装置在结构优化前加速度最大为35 m/s2，峭度为799.175，峰值因子为42.150，振幅幅度不稳定。根据对展开装置的动力学分析，可知改变展开装置的质量分布可以抑制杆件的振动，因此通过改变展开杆的材料，来缩小波动范围，降低振动大小，减少冲击次数。

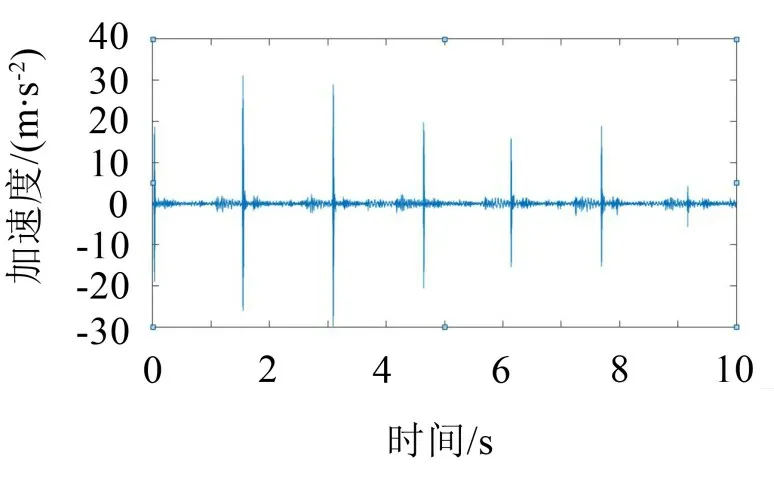
图9 降噪后时域波形图

4.2 改变不同质量分布后的测试试验

选取常用的钢、铝合金、灰铸铁为各杆的试验材料，如表3所示。

表3 展开装置各杆构建材料

根据表3的4个方案，为了保证前后对比的准确性，各个方案仅对各杆的材料进行改变，其他参数设置、环境条件和选取进行对比测点的位置等都相同。再次重复之前的试验步骤，以此达到仅改变质量分布的目的，并测得4组方案的加速度信号，降噪处理后的时域波形如图10所示。

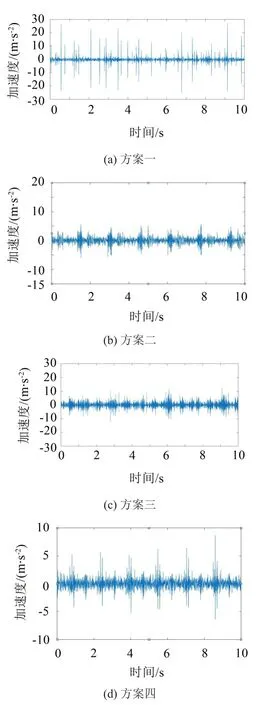
图10 四种不同方案降噪后时域波形图

4.3 结果对比分析

通过对4种不同方案下测得的时域波形图进行分析，可知虽然改变质量分布后振幅有不同程度的降低，但是降低程度和冲击次数又各不相同。首先方案一中，最大振幅为28 m/s2，虽然最大振幅有所降低，但是峭度为374.910，峰值因子为18.585，峰值因子和峭度仍然较大，这样在机器运行时，对于零件还是有较大的影响，易降低装置的运动精度。在方案二中，最大振幅明显降低为7 m/s2，峭度为13.889，峰值因子为6.971，在该方案下冲击情况和振动效果都得到了改善，对零件的损伤得到了降低，而且装置的精度得到了提高。在方案三中，最大振幅为13 m/s2，峭度为13.483，峰值因子为8.477，在该方案下，峭度指标与方案而接近，但是优化效果相比方案二较差，因此方案二较好。方案四中，最大振幅为9 m/s2，峭度为15.243，峰值因子为10.098，虽然在该方案下减振效果较好，但同样相比于方案二来说，方案二的效果更好。因此通过对试验结果的分析，可以得知方案二减振效果最明显。