勾股模糊近似空间的层次结构刻画

宋晶晶, 窦慧莉

(1.江苏科技大学 计算机学院, 镇江 212100) (2.数据科学与智能应用福建省高校重点实验室, 漳州363000)

信息粒是粒计算的基本单元,是一族等价关系、相似关系、邻域关系、模糊关系等组成的对象的集合.文献[1]指出很多领域都存在信息粒,只是表现形式不同. 粒计算包含信息粒、信息粒化之间的关系以及信息粒化的不确定性度量,可以看作是结构化问题求解和信息处理的新范式[2]. 信息粒化使得论域中对象被分成一族不相交或者相互覆盖的信息粒. 粒计算就是找到一些合适的信息粒用来有效近似一个复杂概念，其在智能信息处理过程中有着重要作用.目前，粒计算已经快速发展,成为众多学者研究的热点[3-7].

粒计算理论包含粗糙集、模糊集和商空间等理论,文献[8]提出了模糊集的概念,对模糊现象的描述奠定了基础. 文献[9]基于模糊集提出了直觉模糊集,用隶属度、非隶属度描述决策问题中广泛存在的肯定度和否定度，其在处理不确定性问题时能够更加准确地表达模糊信息.在直觉模糊集中,决策者给出的某一对象x∈A的隶属度与非隶属度之和须满足小于等于1的条件. 近年来,基于直觉模糊集,文献[10-11]进一步提出了勾股模糊集,在勾股模糊集中,隶属度与非隶属度的平方和须满足小于等于1的条件. 当某决策者表达某一备选项满足某一标准的程度时,可能认为隶属度为0.866,非隶属度为0.5,此时隶属度与非隶属度之和大于1,不满足直觉模糊集的条件,但是它们的平方和小于1,所以0.866和0.5可以作为勾股模糊集中的隶属度与非隶属度来描述实际决策问题[4]. 相比于直觉模糊集,勾股模糊集可以表达更丰富的决策信息,在处理不确定性问题时显得更加有效. 已有学者对勾股模糊集进行了研究,文献[12]将勾股模糊集与粗糙集结合,提出了勾股模糊粗糙集,并讨论了勾股模糊粗糙集的若干性质;文献[13]指出了3种勾股模糊数的排序方法的不足,提出了从特征参数完全刻画勾股模糊数的排序的方法;文献[14]以区间模糊偏好关系和直觉模糊偏好关系为依据,将勾股模糊数引入了偏好关系,定义了勾股模糊偏好关系.上述研究对勾股模糊集的发展起到了推动作用[15-19].

信息粒化是粒计算理论中的基本问题,可以看作是信息粒的构建和分解.信息粒化之后,接着分析不同信息粒化之间的关系,合适的信息粒化的选择是问题求解的预处理阶段.从多层次的角度,可以看出层次结构反映了信息粒化的粗细关系.层次结构是多个(偏)序关系的多个层次,每一层代表一个粒度下的抽象表示,不同抽象层次是对理解现实世界问题的不同抽象水平[7].通过有效使用粒度的层次,粒计算可以系统、自然地分析、理解、表示和解决现实世界问题.

文中研究勾股模糊集的信息粒化,以及信息粒化之间的层次结构,以此来表示勾股模糊信息粒化之间的粗细关系.首先给出了勾股模糊信息粒化的表达形式,然后提出了3种序关系来刻画勾股模糊信息粒化之间的层次结构,并结合实例,说明新提出的3种序关系在刻画勾股模糊信息粒化的层次结构的应用.

1 背景知识

1.1 模糊集

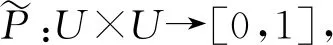
式中：pij∈[0,1](1≤i,j≤n)为对象xi与对象xj之间的相似度,∀xi,xj∈U.

(1)

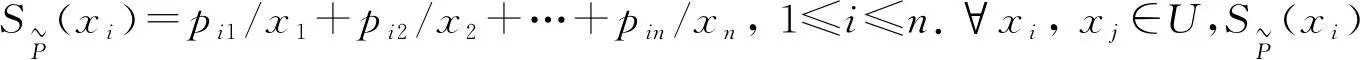
(2)

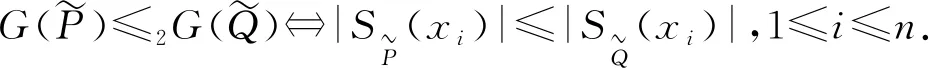
可以看出,序关系≤1是序关系≤2的特例,而序关系≤2又是序关系≤3的特例.作为模糊集的泛化,文献[9]提出的直觉模糊集利用隶属度和非隶属度,可以提供对客观世界更为准确的描述.

1.2 直觉模糊集

1.3 勾股模糊集

与直觉模糊集类似,文献[10]中定义了勾股模糊集.

根据定义4,可以看出直觉模糊集是勾股模糊集的特例.勾股模糊集表达的信息更广泛,更能描述客观世界.

(1)A的补集为{νA(xi),μA (xi)}xi ; (2)A=B⇔μA(xi)=μB(xi)∧νA(xi)=νB(xi); (3)A⊆B⇔μA (xi)≤μB (xi)∧νA (xi)≥νB (xi); (4)A⊂B⇔A⊆B∧A≠B; (5)A∩B=min{μA (xi),μB (xi)},max{νA (xi),νB (xi)}xi ;(6)A∪B=max{μA (xi),μB (xi)},min{νA (xi),νB (xi)}xi .

2 勾股模糊近似空间的层次结构

2.1 勾股模糊信息粒化

定义6令U={x1,x2,…,xn}是一个论域,论域U上勾股模糊关系R的勾股模糊关系矩阵为:

MR=

式中:μR(xi,xj)∈[0, 1]为对象xi与对象xj的相似度；νR(xi,xj)∈[0, 1]为对象xi与对象xj的非相似度,且μR(xi,xj)2+νR(xi,xj)2≤1.

假定文中论域上的勾股模糊二元关系都是自反的,即勾股模糊关系MR中有μR(xi,xi)=1,νR(xi,xi)=0.论域U中所有的勾股模糊关系的集合表示为PFAS=(U, Ω),称为论域U上的勾股模糊近似空间,Ω为论域U上的勾股模糊关系的集合.

定义7勾股模糊近似空间PFAS=(U,Ω)中的勾股模糊信息粒化定义:

K(R)=(SR(x1),SR(x2)…,SR(xn))

论域U上的所有勾股模糊信息粒化空间的集合表示为K(U,Ω),可以看出勾股模糊信息粒化空间和勾股模糊近似空间(U,Ω)存在一一对应的关系,文中不再区分勾股模糊信息粒化空间和勾股模糊近似空间.

经典集合、模糊集、直觉模糊集、勾股模糊集的基数在信息粒化和其不确定性度量中非常重要，介绍勾股模糊集的基数以及勾股模糊信息粒化之间的操作算子交、并和补.

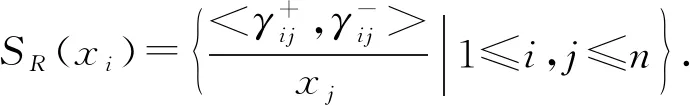
对应的勾股模糊信息粒化的隶属度基数、非隶属度基数和犹豫基数可以定义为:

定义10令K(P)=(SP(x1),SP(x2),…,SP(xn))∈K(U,Ω),K(Q)={SQ(x1),SQ(x2),…,SQ(xn)}∈K(U,Ω),其中

勾股模糊信息粒化K(P)和K(Q)之间的操作算子交、并和勾股模糊信息粒化K(P)的补定义为:

K(P)∩K(Q)=

{SP∩Q(xi)|SP∩Q(xi)=SP(xi)∩SQ(xi),1≤i≤n},

K(P)∪K(Q)=

{SP∪Q(xi)|SP∪Q(xi)=SP(xi)∪SQ(xi),1≤i≤n},

SP(xi)∩SQ(xi)=

SP(xi)∪SQ(xi)=

推论2令K(P),K(Q),K(R)∈K(U,Ω),勾股模糊集的交并补算子满足以下定律:

(1) 交换律:K(P)∩K(Q)=K(Q)∩K(P),

K(P)∪K(Q)=K(Q)∪K(P).

(2) 结合律:

K(P)∩(K(Q)∪K(R))=(K(P)∩K(Q))∪(K(P)∩K(R)),

K(P)∪(K(Q)∩K(R))=(K(P)∪K(Q))∩(K(P)∪K(R)).

(3) 吸收律:

K(P)∩(K(P)∪K(Q))=K(P)∪(K(P)∩K(Q))=K(P).

(4) 德摩根律:

2.2 勾股模糊近似空间的层次结构

文中提出3种序关系来刻画勾股模糊近似空间的层次结构,用来比较勾股模糊信息粒化的粗细关系.

定义11令K(P)=(SP(x1),SP(x2),…,SP(xn))∈K(U,Ω),K(Q)={SQ(x1),SQ(x2),…,SQ(xn)}∈K(U,Ω),其中,

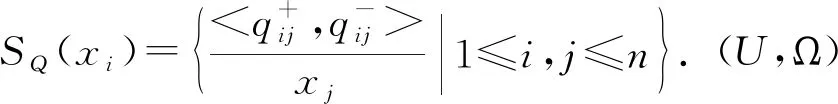
(1)P1Q⟺K(P)1K(Q)⟺SP(xi)⊆SQ(xi)⟺

P=Q⟺K(P)=K(Q)⟺SP(xi)=SQ(xi)⟺

P1Q⟺K(P)1K(Q)⟺

K(P)1K(Q)∧K(P)≠K(Q).

(2)P2Q⟺K(P)2K(Q)⟺

|SP(xi)|+≤|SQ(xi)|+∧|SP(xi)|-≥SQ(xi)|-⟺

Pi+≤Qi+∧Pi-≥Qi-,1≤i,j≤n;

P≈2Q⟺K(P)≈2K(Q)⟺

|SP(xi)|+=|SQ(xi)|+∧|SP(xi)|-=SQ(xi)|-⟺

Pi+=Qi+∧Pi-=Qi-,1≤i≤n;

P2Q⟺K(P)2K(Q)⟺

K(P)2K(Q)∧K(P)≈2K(Q).

(3)P3Q⟺K(P)3K(Q)⟺

|K(P)|+≤|K(Q)|+∧|K(P)|-≥|K(Q)|-⟺

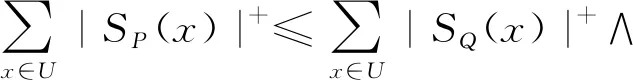
P≈3Q⟺K(P)≈3K(Q)⟺

|K(P)|+=|K(Q)|+∧|K(P)|-=|K(Q)|-；

P3Q⟺K(P)3K(Q)⟺

K(P)3K(Q)∧K(P)≈3K(Q).

推论3令K(P),K(Q),K(R)∈K(U,Ω),则：

(1)K(P)iK(Q)⟺K(Q)CiK(P)C(i=1,2,3)；

(2)K(P)∩K(Q)iK(P) (i=1,2,3)，

K(P)∩K(Q)iK(Q) (i=1,2,3)；

(3)K(P)iK(P)∪K(Q) (i=1,2,3)，

K(Q)iK(P)∪K(Q) (i=1,2,3).

推论4序关系i是序关系i+1(i=1,2)的特例.

第一个序关系定义在两个勾股模糊信息粒之间的勾股包含关系中,第二、第三种序关系定义在勾股模糊信息粒和勾股模糊信息粒化的基数上.可以看出1是一个偏序关系,2和3分别是(U,Ω)和K(U,Ω)上的预序关系,因为它们不满足反对称.另外,以下关系成立:1⟹2⟹3.

文中通过一个实例来说明提出的3种序关系在勾股模糊近似空间中的应用.

例1令U={x1,x2,x3,x4},论域U上的勾股模糊二元关系Ri由如下的矩阵表示:

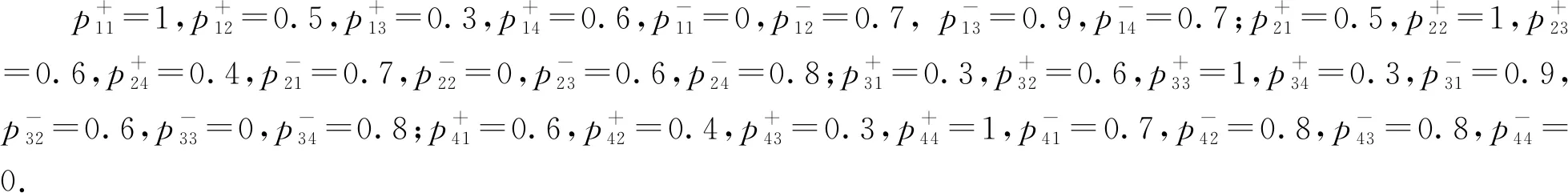
比较勾股模糊信息粒R1和勾股模糊信息粒R3，勾股模糊二元关系R1中,有|SR1(x1)|+=2.4,|SR1(x2)|+=2.5,|SR1(x3)|+=2.2,|SR1(x4)|+=2.3,|SR1(x1)|-=2.3, |SR1(x2)|-=2.1, |SR1(x3)|-=2.3, |SR1(x4)|-=2.3；在勾股模糊二元关系R3中,有|SR3(x1)|+=2.4,|SR3(x2)|+=2.6, |SR3(x3)|+=2.6, |SR3(x4)|+=2.4, |SR3(x1)|-=2.2,|SR3(x2)|-=2.0,|SR3(x3)|-=2.1,|SR3(x4)|-=2.3.

可以看出, ∀x∈U,|SR1(x)|+≤|SR3(x)|+且|SR1(x)|-≥|SR3(x)|-,故有K(R1)2K(R3),说明勾股模糊信息粒R1比勾股模糊信息粒R3要细.

比较勾股模糊信息粒R1和勾股模糊信息粒R4，在勾股模糊二元关系R1中,有|K(R1)|+=9.4,|K(R1)|-=9.0；在勾股模糊二元关系R4中,有|K(R4)|+=9.0,|K(R4)|-=9.4.可得|K(R1)|+≥|K(R4)|+且|K(R1)|-≤|K(R4)|-,故有K(R4)3K(R1),说明勾股模糊信息粒R4比勾股模糊信息粒R1要细.

2.3 勾股模糊近似空间的格结构

文献[21-22]从集合距离的角度,使用格结构刻画清晰近似空间的信息粒化的层次结构.文献[23]提出利用知识距离格来刻画覆盖近似空间的信息粒化的层次结构.文中将讨论勾股模糊近似空间在偏序关系≼1上的格结构.

定义12令(L,≤)是一个偏序集,L上的两个算子∧和∨:L2→L,存在以下关系:

(1) ∀a,b∈L,a∧b=b∧a,a∨b=b∨a；

(2) ∀a,b,c∈L, (a∧b)∧c=a∧(b∧c), (a∨b)∨c=a∨(b∨c);

(3)a∧b=b⟺b≤a,a∨b=b⟺∀a,b∈L,a≤b则称(L,≤)是一个格;

(4) 如果(L,≤)是一个格,且∀a,b,c∈L,a∧(b∨c)=(a∧b)∨(a∧c),a∨(b∧c)=(a∨b)∧(a∨c),则称(L,≤)是一个分配格;

(5) 如果(L,≤)是一个格,且∀a∈L,a-1∈L存在(a-1)-1=a且a≤b⟺b-1≤a-1则称(L,≤)是一个有补格;如果存在0, 1∈L使得∀a∈L, 0≤a≤1,则称0和1分别是最小元素和最大元素.

结合定义11和12以及推论1,可以得出如下结论:

定理1定义在勾股模糊信息粒化空间K(U,Ω)上的操作算子∩,∪和C如定义11,则(K(U,Ω),1, ∩,∪,C)是一个有补分配格.

证明:根据定义10和定义11,明显得证.

3 结论

粒计算理论把复杂的问题进行抽象,转化为简单的问题,更利于对问题进行分析和解决.勾股模糊集作为一种重要的粒计算模型,在处理问题时可以更客观的描述现实世界.文中以勾股模糊集为主要研究对象,首先给出了勾股模糊信息粒和勾股模糊信息粒化的表示方法,其次给出了勾股模糊信息粒化的基数表示,最后根据勾股模糊信息粒化之间的关系,用实例给出了3种序关系在勾股模糊近似空间中的应用，并且给出了偏序关系≼1上的格结构,对勾股模糊近似空间的层次结构进行了刻画.

下一步工作将研究勾股模糊信息粒化不同层次上的约简,以及对勾股模糊信息粒化的不确定性程度进行刻画,进一步丰富粒计算理论的研究.