带阻尼项的g-Navier-Stokes方程的全局吸引子

刘文婧，姜金平，熊坤翠

(延安大学 数学与计算机科学学院，陕西 延安 716000)

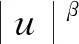
(1)

其中g=g(x1,x2)是定义在(x1,x2)⊂Ω上的合适的光滑实值函数，满足00是两个常数，u和p表示速度和压力。如果c=0，g(x1,x2)=1，则方程为通常的二维Navier-Stokes方程。

ROH于2001年提出了二维g-Navier-Stokes(g-N-S)方程后[1]，g-N-S方程被学者广泛研究，当下已有一些研究成果[2-9]，但g-N-S方程加入非线性阻尼项时，它的长时间行为尚无结果，本文通过验证解半群存在有界吸收集和满足渐近紧性建立含非线性阻尼项的g-N-S方程的全局吸引子的存在性。

1 预备知识

定义1.1[10-12]若{S(t)}t≥0为Banach空间X上的半群。当集合∈X且具有性质：

引理1.1[13](Gronwall’s Inequality)令x(t)∈R满足不等式，

则，

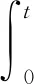
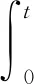
引理1.2[14](Gagliardo-Nirenberg Inequality)令Ω=Rn或Ω⊂Rn为带有光滑边界∂Ω的一个有界域，u∈Lq(Ω)，Dmu∈Lr(Ω)，1≤q，r≤∞，则存在一个常量c使得，

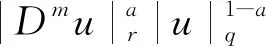
其中，

c依赖于n,m,j,a,q,r。

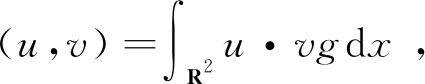
设R2上具有紧支集的C∞函数的集合为D(R2)，令，

D={v∈(D(R2))2;▽·gv=0,∀v∈R2}。

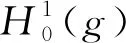
D(A)=(L2(g))2∩Vg

定义一个g-Laplacian算子：

利用上式将方程(1)写作如下形式：

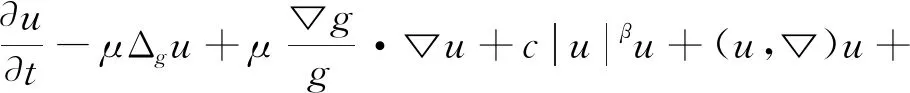
(1.1)

若将g-正交投影Pg:L2(g)→Hg作用于式(1.1)上，则可得方程(1.3)，设f∈Vg，u0∈Hg，u∈L∞(0,T;Hg)∩L2(0,T;Vg),T>0

(1.2)

使得，对∀t>0，

(1.3)

其中，bg:Vg×Vg×Vg→R满足，

(1.4)

则式(1.3)与(1.5)等价。

(1.5)

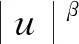
〈Agu,v〉=((u,v)),∀u,v∈Vg

(1.6)

(1.7)

2 解和吸收集的存在性

命题2.1若f∈L2(g)，u0(x)∈Hg，则方程(1.1)一定存在唯一的解，

u(x,t)∈L∞(R+;Hg)∩L2(0,T;Vg∩C(R+;Hg)(∀T>0)，使得式(1.3)成立。

证明证明过程类似于ROH[2]定理3.1。下面证明吸收集的存在性。

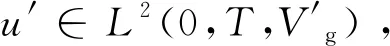
故由 (1.5)

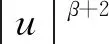
因bg(u,u,u)=0,∀u,v∈Vg,故有，

(2.1)

则，

因此，

(2.2)

利用引理1.1，得，

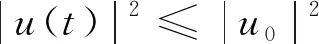
(2.3)

在[0，t]积分得，

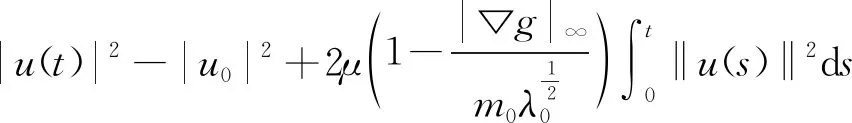
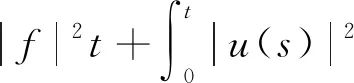
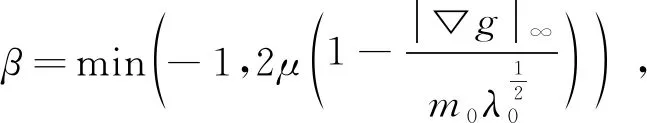
(2.4)

由命题2.1，可在Hg中定义一个连续半群{S(t)}t≥0,使得，

S(t)u0=u(t),t>0

其中，u(t)是满足u(0)=u0∈Hg的(2.3)的解，此外，由式(2.3)可得，

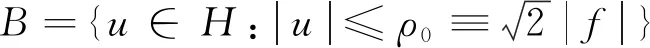
(2.5)

是半群在Hg中的吸收集。

定理2.1{S(t)}t≥0为完备度量空间X上的连续半群。

证明证明过程与文献[6]命题2.2类似。

命题2.2假设u0∈V,f∈H，则存在一个常量ρ1和时间t1使得，

|Agu(t)|2≤ρ1，对于t≥t1

证明由(1.5)1，应用Minkowski不等式，有，

μ|Agu|2≤|ut|2+|B(u)|2+c|uβu|2+|f|2+μ|Ru|2

(2.6)

由[13]

因此

(2.7)

应用引理1.2得，

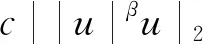
=c1。

(2.8)

由(2.6) (2.7) (2.8)得，

≤c2。

对于t≥t1。

故存在一个正常量ρ1，使得，

|Agu(t)|2≤ρ1，对于t≥t1。

命题2.3假设u0∈V,f∈H，则存在常量I1,ρ2和时间t1使得，

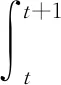
|ut(s)|≤ρ2，对于t≥t2

证明过程参照命题2.2和文献[16]中命题6。

3 半群的紧性

引理3.1[15]令X是一个完备度量空间，{S(t)}t≥0是上X的连续半群，则{S(t)}t≥0在X上有一个全局吸引子当且仅当，

(1){S(t)}t≥0在X中存在有界吸收集；

(2){S(t)}t≥0在X上是渐近紧的。

证明由定理2.1，{S(t)}t≥0是连续半群，因为在(3.5)式中定义的B是吸收集，我们只需要证明半群的渐近紧性，令un(t)=S(t)u0n，wn(tn)=

则由(2.5)有，

μAgun(tn)=f-wn(tn)-B(un(tn))-G(un(tn))-μR(un(tn))

(3.1)

由命题2.2和命题2.3得存在T>0，对所有tn≥T的

(3.2)

因为tn→∞，存在一个N>0使得t≥T对所有的n≥N。

因此由(3.2)，有，

|Aun(tn)|2≤ρ1

(3.3)

由Aubin-lions引理得，存在w∈Vg，v∈D(A)使得，

wn(tn)在Hg中强收敛到w。

(3.4)

un(tn)在Vg中强收敛到v。

(3.5)

由[16]

‖un(tn)‖∞≤c,∀n≥N

因此由(3.5)，有，

则G(un(tn))在H中强收敛到G(v)。

(3.6)

由[16]得B(un(tn))在H中强收敛到B(v)。

(3.7)

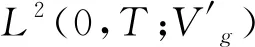
∀v∈Vg,00

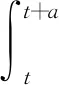
cT‖v‖(un(tn)-v)1/2。

其中cT>0是独立于n的正常数，则对v=R(un(tn))-R(v)，一定有，

cT(un(tn)-v)1/2‖R(un(tn))-R(v)‖；

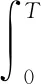
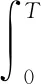
则由(3.5)可得出R(un(tn))强收敛到R(v)。

(3.8)

则由(3.4) (3.6) (3.7) (3.8)得μAgun(tn)→f-w-G(v)+B(v)-μRu(v),n→∞。

这说明半群{S(tn)un}在Hg中是相对紧的，因此，{S(t)}t≥0在Hg中满足渐近紧性。因{S(t)}t≥0在Hg中存在有界吸收集B,故证明了全局吸引子的存在性。

4 结论