一类非线性级联系统层次化执行器故障诊断方法研究

张 梅，李泽滔*，DAHHOU Boutaied

(1.贵州大学 电气工程学院，贵州 贵阳 550025;2.University Paul Sabatier，LAAS-CNRS，法国 图卢兹 F340100)

随着控制系统规模化、集成化和智能化发展，系统通常是由若干设备协同运行的复杂互联耦合系统，系统动态特性日趋复杂，故障的发生不可避免；任一系统设备元件出现故障而又未能及时发现,其结果不仅会导致设备损坏,还可能造成全局系统性能下降及非正常停运，甚至是灾难性后果。因此，为保障系统的可靠性和安全性，迫切需要对全局系统及各个设备的实时性能和运行状态进行监测、评估和故障诊断,从而采取有效措施,保证系统及设备的稳定运行[1-5]。

在故障诊断的研究中，执行器故障诊断吸引了工业界和学术界学者的广泛关注。针对执行器故障诊断问题，国内外学者从3个方面进行了研究。一类是系统级故障诊断方法，旨在从全局系统角度检测故障并隔离出故障执行器，而忽略执行器内部动态特性，不针对引起现场设备故障的内部参数[2-16]。一类重要方法是基于残差生成理论的方法[2-10]。残差定义为测量值与其估计值之间的差异，当残差超过其阈值时，故障被诊断并隔离，常见残差生成方法有：高增益观测器[3]，自适应观测器[9]，区间法[10]等。另一种方法是故障估计或故障重构方法[11-16]，这类方法可确定故障的大小、位置及其动态过程。常见故障重构的方法：滑模观测器[12]，未知输入观测器[14]，输入重构法[15]等。然而，由于对设备内部变量的不完全识别，系统级方法不能定位执行器内部的故障点，使得维护人员根据故障提示往往找不到故障原因，无法及时消除故障。

另一类是设备级故障诊断方法，旨在分析特定执行器的内部动态特性，识别引起执行器故障的内部参数[17-22]。一类广泛深入的研究是基于数据驱动的方法[17-19]，如神经网络，支持向量机，小波分析，谱分析等。如文[19]将FFT与数据驱动的方法进行结合, 研究不同位置IGBT的开路故障；另一类研究的方法则是基于模型的故障诊断技术[20-22]。如文[1]中讨论了高速列车牵引系统中的牵引电机等重要部件和单元的故障诊断技术。文献[22]中利用滑模观测器对气动执行机构进行故障诊断研究。然而，设备级故障诊断仅监测设备本身，缺乏对全局系统的动态信息的监督，而设备内部故障会产生连锁反应，影响全局系统的最终输出。

此外，也有少数系统级和设备级相结合的层次化故障诊断方法研究，旨在关注故障在系统各层级的传播分析，及子系统参数故障对系统终端的影响[23-26]。如文献[24]中从高速列车牵引系统关键部件到整车,展开故障诊断、容错控制与故障预测研究的综述。文献[25]探讨了从全局余热锅炉接近点层面研究对汽包液位控制阀的破坏作用。文献[1]中也提到未来的研究方向是整体系统与各设备子系统结合。

基于上述认识，本文提出了一种能够解决非线性系统故障诊断的层次化故障诊断方法。利用全局系统提供的可测信息，识别执行器内部故障参数，改善故障定位并提供更好的预测维护帮助。该方法强调了现场设备动态特性的重要性，更具有故障针对性。

1 问题描述

将执行器及过程对象视为全局控制系统的子系统，构建一个非线性动态互连系统，如图1所示。目的是在全局系统故障时，通过全局系统输出y的变化，识别出执行器子系统内部具体的故障参数v(vi,i=1,…,k)，并对建模不确定性及测量噪声d鲁棒。故障vi表示引起执行器故障的原因，如阀门泄漏，堵塞等。

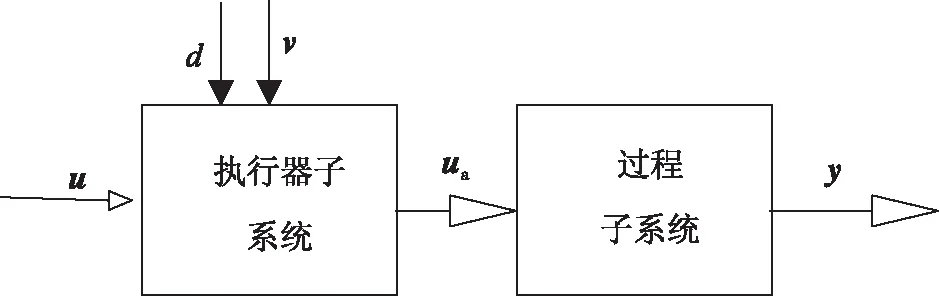
图1 级联系统结构

考虑过程子系统是MIMO输入仿射非线性系统，由(1)描述：

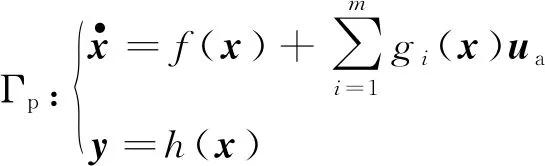
(1)

其中:矢量x∈M是过程子系统状态，n维平滑流形,f,gi是M上的平滑矢量场，ua∈Rm是过程子系统的输入，也是执行器的输出，假设不可测量，y∈Rp是整个系统的输出。

考虑执行器子系统由(2)描述：

(2)

其中:xa∈Rn是状态变量，u∈Rl是输入，xa∈Rm是执行器子系统的输出，也是过程子系统的输入。

这样两个子系统∑a和∑p子系统就构成非线性动态级联系统∑，级联系统输入为u，而输出向量为y。

如果故障v是执行器参数或其他干扰信号的集合，则得到故障模式为：

(3)

其中:v(t)为故障信号(v1,…,vm)，其元素vi:[0,+∞)→R是任意的时间函数。

考虑由式(1)和(3)所描述的非线性级联动态系统故障模型，研究目标是描述子系统变量与全局系统输出之间的因果关系，即产生故障的参数变化,从而为运行中的控制系统提供先进的预测维护手段。

2 故障可识别性条件

要使得由执行器子系统提供的(3)中的故障信息vi(i=1,…,k)对(1)中的系统输出y的影响可以严格区分,如果将整个级联动态系统视为一个黑盒子，这个问题可以视为输入可观测性问题，其中V是整个系统的未知输入，Y是输出。而输入或故障可观测性是等价于系统的左可逆性，如文献[15]所示。因此，如果整个互连非线性动态系统是可逆的，则可以从系统输入u，系统输出y及其导数重建故障向量V。可见，动态互连系统故障可识别的条件是故障模式下非线性动态互连系统的可逆性。

定义1如果故障vi(i=1,…,k)对由(1)和(3)描述的非线性动态互连系统是代数可观测的，就说故障vi(i=1,…,k)是可诊断的。

性质1如果可以从(1)和(3)描述的非线性动态互连系统的可测量值估计故障信号vi(i=1,…,k)，则认为故障vi(i=1,…,k)是可诊断的。

性质2如果由(1)和(3)描述的非线性动态互连系统是可逆的，则可以通过系统测量输出y,获得故障信号vi(i=1,…,k)。

定理1如果(1)和(3)描述的非线性动态互连系统是可逆的，则认为故障vi(i=1,…,k)对系统输出y具有可区分的影响。

3 互联观测器设计及故障检测

为实现级联系统的状态检测及故障检测，设计了如图2所示的互联观测器，目标是使用输入u和输出y的测量值在线准确地估计每个子系统的状态向量x和xa，以及未知测量的互连向量ua，并在故障发生时及时进行故障检测生成残差。

图2 互联观测器结构

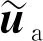
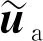
3.1 观测器设计

为了估计执行器非线性动态子系统的状态，不失通用性，公式(2)中描述的执行器子系统可以转换成以下标称形式[26]：

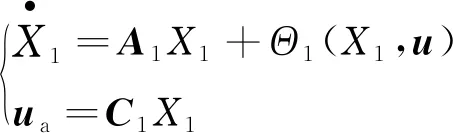
(4)

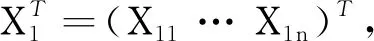
C1=[1 0 … 0]。

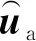
(5)

定义z=[z1z2]=[xua], 则系统 (1) 可扩展为:

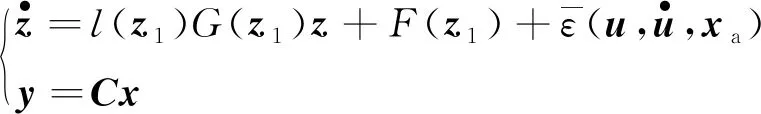
(6)

其中,

In为n×n单位阵,l(z1)是一个标量实函数，αl≤|l(z1)|≤βl。

(7)

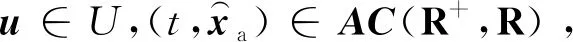
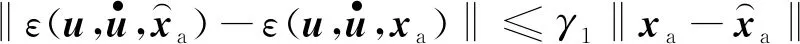
(8)

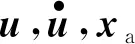
则可以设计系统(6)的扩展高增益观测器(9)：

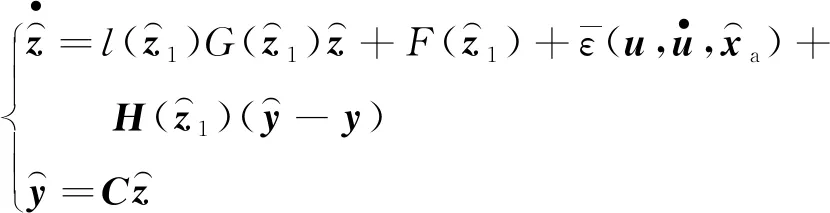
(9)

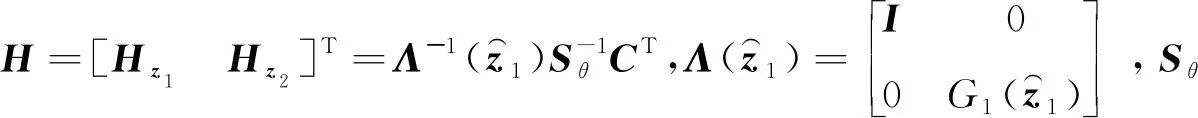
θSθ+ATSθ+SθA-CTC=0

(10)

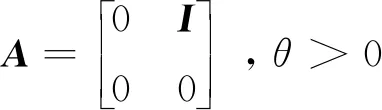
那么,估计器的增益可以由下式给出：

系统(6)与(9)一起构成了所设计的互连非线性动态系统的观测器(11)：

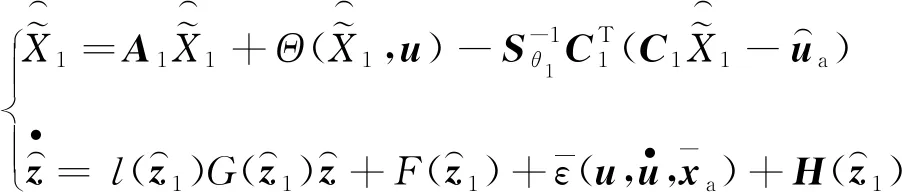
(11)

3.2 输入重构

对如(1)所示的输入仿射非线性动态系统，按照文[15]给出的系统求逆的算法，可得：

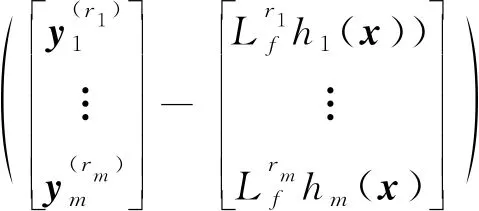
通过构造:

以下是观测器的结构:

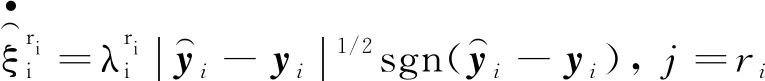
结合逆系统输入重构及输出导数估计值，得到代数重构未知输入表达式：

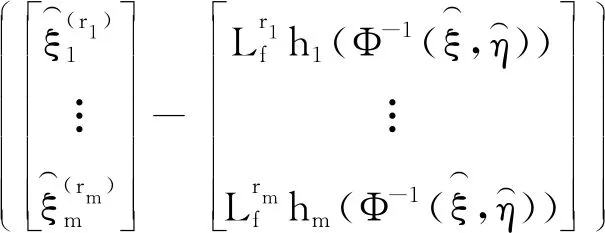
3.3 故障检测

观测器(11)的估计误差满足等式：

定义：

(12)

令r0(t)为故障检测的残差：

r0(t)=d‖e0(t)‖/dt

(13)

那么有：

(14)

其中,ε是阈值。

4 故障根本原因识别

1≤j≤m,1≤i≤k,t≥tf

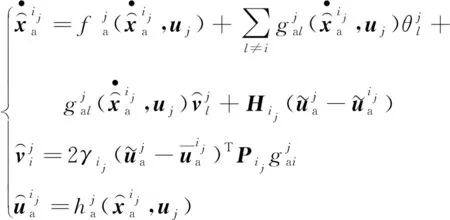
(15)

借助于(15)可以计算矩阵Pij。其中,Qij是可以自由选择的正定矩阵：

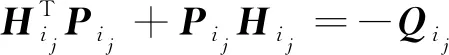
(16)

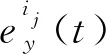
将故障根本原因RCA(root cause analysis)残差定义为:

残差设计为对来自特定执行器特定故障原因敏感并且对所有其他执行器的故障原因“较不敏感”。对于第j个执行器，如果故障是由第i个故障原因引起的，则第i个RCA残差将超过其阈值，不会再次恢复为零，而另外(k-1) 残差将保持低于其阈值。因此，RCA滤波器的设计目的是为了识别特定的执行器故障原因。

5 仿真验证

以多功能换热反应器为对象，详见文[26]。对系统中的几种典型故障进行仿真与分析，结果表明，所提出的方法能够较全面地反映局部故障对系统局部及全局的动力学影响，对获取系统完整的故障模型及分析系统故障运行状态具有较高的应用价值。

5.1 换热器模型

(17)

其中,

y1=x1,y2=x2。

5.2 控制阀数学模型

同样，根据文[26]，执行器故障可能由参数μ,k,u,Δp变化引起, 那么在两个执行器中有8个相关参数：[k1μ1k2μ2pc1pc2ΔP1ΔP2] 。故障根本原因分析(RCA)实际就是识别这8个参数的异常变化的过程。执行器故障模型为仿射型式的模型。

V=[v1v2v3v4v5v6v7v8]T=

[k1μ1k2μ2pc1pc2ΔP1ΔP2]T

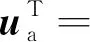
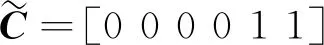
扩展执行器子系统为：

(18)

其中,

ga(xa)=

对于大多数部件而言，在工业实践中观察到的执行器故障的原因都是单个数导致的，很少发生多个参数故障。

5.3 仿真结果及分析

本仿真实例的数据来自一个实验用逆流式换热反应器。如文[26]所示，此实验用换热反应器由法国图卢兹LGC 实验室设计制造，它由3块反应板和5块冷却板以三明治结构组合在一起，如图3所示。

图3 实验用集成换热反应器

仿真目的是验证所开发的系统监督及故障诊断策略的有效性。仿真操作条件如下：冷却流体流速Fu参考值为4.22e-5m3/s, 过程流体流速Fp参考值为4.22e-6m3/s。观测器初始条件0。执行器子系统参数值:m=2 kg，Aa=0.029 m2,μ=1 500 N·s/m，k=6 089 N/m 冷却流体阀Pc为1 MPa,过程流体阀为1.2 MPa，冷却流体阀差压 ΔP为 0.6 MPa，过程流体阀60 kPa。

图4为在无故障情况下两流体流速的估计值，黑色实线为理想计算值，绿色点化虚线为互连观测器的估计值，红色虚线为系统逆方法的重构值。从图4可见，在理想情况下，3个估计值收敛重合。

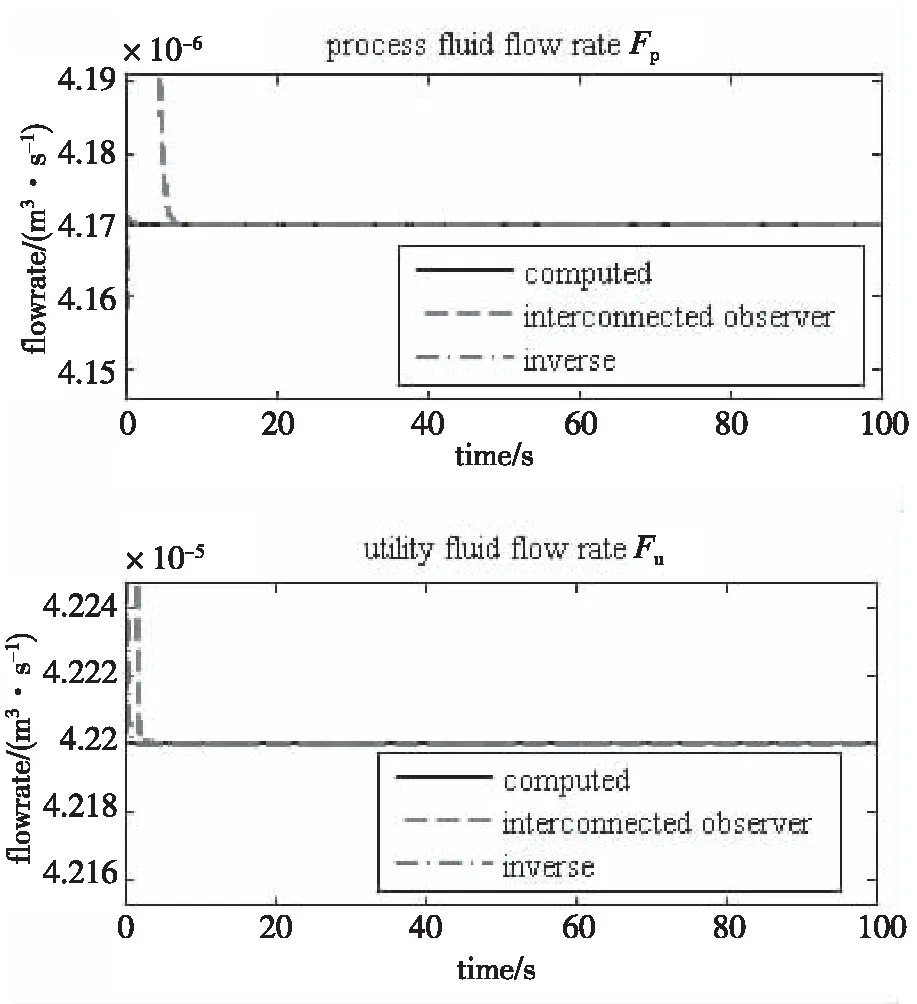
图4 不同方法的流体流速估计值

实际生产中执行器故障通常由单参数故障引起。因此，考虑每个执行器只有一个故障，则执行器子系统中可能会同时发生两个故障。为了说明所提出的方案的鲁棒性，考虑外部干扰或测量噪声，假设输出测量值y被有色噪声破坏，有色噪声由具有零均值和单位方差的高斯白噪声激发的二阶AR滤波器产生，标准偏差约为3.5。

每个执行器分别考虑一个故障。对过程流体执行器，考虑参数k1发生了故障，产生此故障的原因可能是泄漏。对冷却流体执行器则考虑参数pc2发生了故障，引起故障的原因可能是阀门堵塞，也是控制阀中最常见的故障。如果没有妥善维修，这种故障可能会对系统性能造成严重影响。图5—6给出了仿真结果。

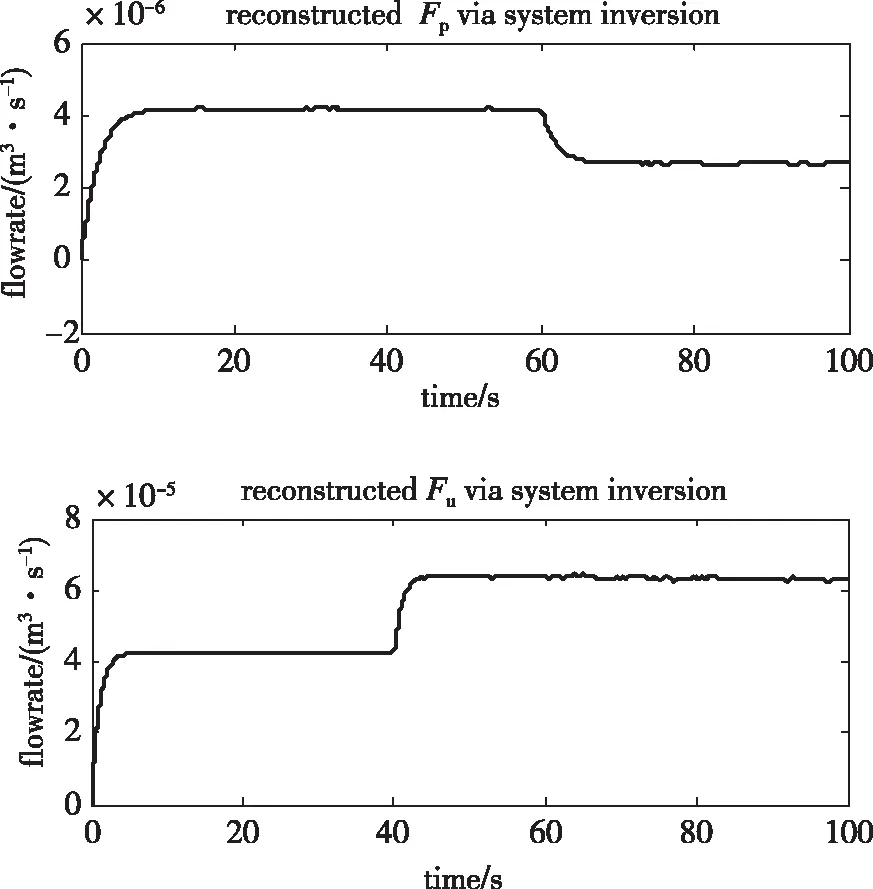
图5 重构的流体流速

从图5可见，虽然存在噪声，但是开发的输入重构技术仍然可以提供具有良好精度的重构输入。在过程流体执行器中，重构的流体流速在60 s时突然下降并花费4 s达到新的稳态，由于参考流速为定值，因此流速的突然下降表明有故障发生。对于冷却流体执行器，重构的流速值在60 s时开始增加，且经过3 s后达到新平衡。此意外的增长也意味着故障的发生。应该注意到，虽然Fp,Fu在观测器中初始轨迹不同，他们最终都收敛到各自的“真值”。

从图6得到，故障检测残差r1表示过程流体执行器的故障。r1在60 s时产生突变且值大于其阈值，也就是检测到故障的发生。故障检测残差r2对应的是过程流体执行器的故障检测，因此r2在40 s的突变表征了过程流体执行器故障。可以通过增大观测器增益或者减小阈值的方式来缩短故障的检测时间，但是大增益和小阈值有可能造成故障的不能正确检测，因为大增益的观测器对噪声会很敏感，而小阈值可能与噪声无法分开而造成误判。因此，为了能正确检测故障，需要在故障可检测性与灵敏性间做平衡选择。在存在噪声的情况下可能无法检测到小幅度故障。在检测到故障之后，下一步就是确定产生故障的根本原因。

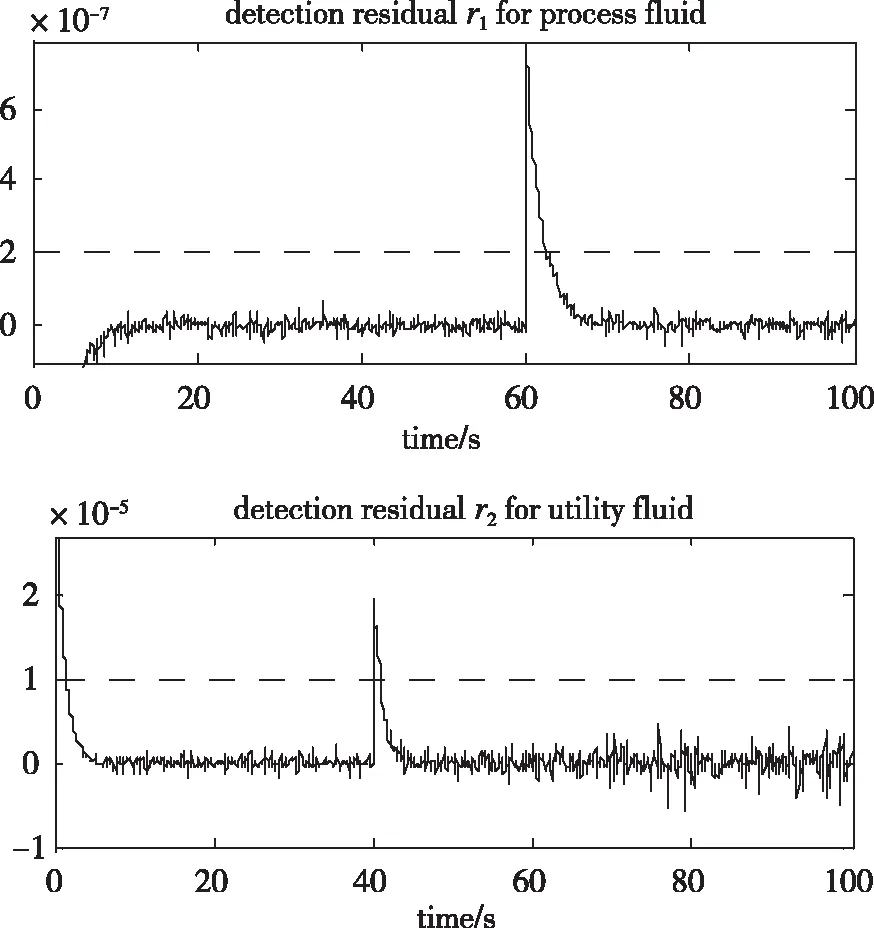
图6 故障检测残差

图7—8给出了故障根本原因残差RCA，s11,s12,s13,s14分别对应过程流体执行器可能的参数故障μ1,k1,pc1,ΔP1；同理，s21,s22,s23,s24分别对应过程流体执行器可能的参数故障μ2,k2,pc2,ΔP2。

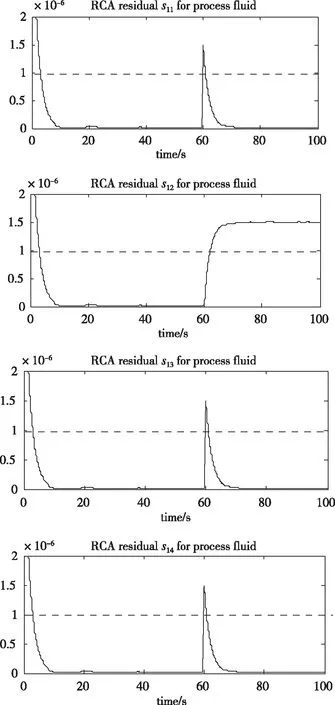
图7 识别过程流体执行器参数故障的RCA残差

从图7可见，在60 s时，所有RCA残差都开始变化并超过其阈值，但只有RCA残差s12超过其阈值且保持不变，其余的RCA 残差都在一段时间后小于其各自的阈值，因此产生过程流体执行器故障的原因，即参数k1就被隔离出来了。对于冷却流体执行器的故障而言，从图8可见，从40 s开始，RCA残差开始变化，只有RCA残差s23大于其阈值并保持在阈值之上，这就意味着产生此执行器故障的原因是故障源pc2引起的。

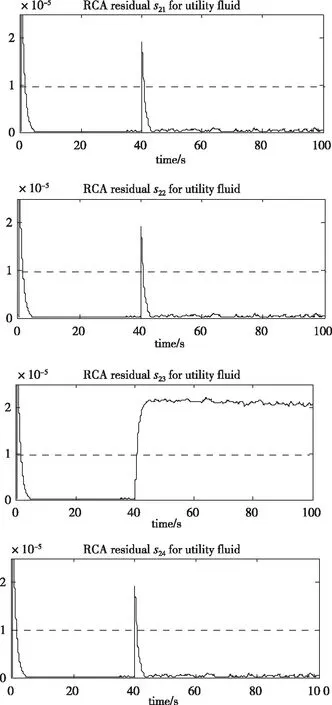
图8 识别冷却流体执行器参数故障的RCA残差

从上述仿真结果可以看出，提出的策略可以正确检测和定位故障，并且以准确的精度实现了每个检测故障的根本原因分析。由于所提出的方案的鲁棒性能，获得了令人鼓舞的仿真结果。

6 总结

本文研究了一类非线性动态互连系统的故障诊断和故障根本原因分析的问题。通过在RCA滤波器中使用全局系统的输出来估计本地子系统的输出，将本地故障参数识别能力与全局系统监控能力有机结合起来。另外，还研究了故障的可诊断性条件。仿真结果验证了所提出设计方法的有效性和鲁棒性。