分布式干扰波束形成及其性能影响因素分析

于周吉

(海军装备部，北京 100036)

0 引 言

传统的集中式大功率干扰设备隐蔽性差，易被敌方雷达探测，招致反辐射攻击。同时，受限于平台尺寸和高功率微波器件的技术发展水平，干扰设备的功率很难提升。基于无人机等小型化平台，将多个小功率干扰机在空间分散布置，通过对多个分布式干扰节点进行幅度相位加权，使各节点的干扰能量在目标方向同相叠加，可以形成高增益定向波束，获得提升干扰功率、降低敌方雷达探测距离的效果。

利用多个干扰节点形成具有相干性的干扰波束的问题与分布式通信系统中的波束形成问题类似。文献[1]对无线传感器网络中的分布式发射波束形成技术进行了研究，重点设计了可扩展载波同步方案；文献[2]分析了节点本振误差对分布式通信系统的发射波束形成性能的影响；文献[3]以任意阵平均波束图为指标分析了频率跳变对发射波束形成性能的影响。基于分布式通信系统中发射波束形成技术的研究成果，文献[4]主要研究了时变条件下基于有限反馈的分布式干扰波束形成，但前提条件是在目标处存在一个己方反馈节点，这一要求在实战中难以满足。针对分布式干扰波束形成中的栅瓣问题，文献[5]着重研究了干扰节点的位置优化问题。

目前，少有文献对分布式干扰波束形成性能进行系统性分析。本文建立了分布式干扰波束形成的系统模型，推导了理想条件下任意阵的归一化平均功率方向图，理论分析了相位误差和位置误差对分布式波束形成性能的影响，并对分布式波束形成的性能进行了仿真。

1 系统模型

分布式干扰波束形成系统的数学模型如图1所示。N个干扰节点随机分布在底面半径为L、高为2H的圆柱区域内，以该圆柱区域的中心为坐标原点O，建立三维坐标系，N个节点在封闭区域内均匀分布。记干扰节点i的位置为(xi,yi,zi)，和原点O的距离为ri，i=1,2,…,N，目标位于YOZ平面内，位置为(xT,yT,zT)，和原点O的距离为RT，空间任意点坐标为(x,y,z)。

图1 分布式干扰波束形成系统的数学模型示意图

不同于球坐标系，为方便数学表达，定义θ为任意点(x,y,z)与XOY平面的夹角，φ为任意点(x,y,z)与YOZ平面的夹角，定义R为任意点(x,y,z)到坐标原点的距离，则：

(1)

同时，为便于讨论，假设系统满足以下理想条件：

(1) 各干扰节点具有全向辐射特性，且发射功率相同，取为1；

(2) 各干扰节点间隔足够大，互耦可忽略；

(3) 各干扰节点到目标处的路径损耗都相同(实际上，不同节点到目标处的路径差别相对很小)，取为1；

(4) 各干扰节点极化方向和被干扰对象的极化方向完全匹配。

根据阵列天线理论，通过改变各干扰节点发射信号的幅度和相位，可以得到任意波束指向的方向图，实现波束扫描。方向图的主要特性参数有波束宽度、副瓣电平和波束形状等。干扰节点i的复加权系数ωi可表示为：

ωi=Aiejφi

(2)

式中:Ai为幅度加权系数，通常各干扰节点幅度加权系数相同，可认为Ai≡1；φi为相位加权系数。

由于各干扰节点具有全向辐射特性，取方向图函数为1，根据方向图乘积原理，则分布式干扰波束形成系统的场强方向图可表示为：

(3)

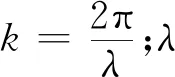
在远场条件下，R≫ri，因此，Di(θ,φ)主要由R决定，ri的变化对Di(θ,φ)的影响很小，可认为Di(θ,φ)=R-riαi(φ,θ)。

显然，为使信号能够在目标点处同相叠加，干扰节点i的载波应预补偿相位φi=kDi(θT,φT)，则：

(4)

远场条件下，可认为R=RT，则：

F(θ,φ)=

(5)

由于假设目标位于YOZ平面内，所以φT=0，令：

(6)

则：

(7)

定义归一化功率方向图为：

(8)

显然，当θ=θT,φ=φT时，|F(θ,φ)|2取得最大值N2，则：

(9)

当节点的数量比较多时，根据大数定理，分布式波束形成一般会获得平均波束特征，定义归一化平均功率方向图为：

Pav(θ,φ)=E{P(θ,φ)}

(10)

根据xi和yi以及zi的分布密度函数，可以得到：

(11)

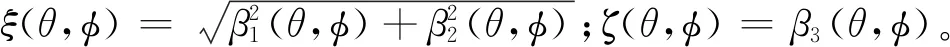
实际中，由于相位误差和距离误差的存在，分布式干扰波束形成的性能会受到影响，影响相位误差的主要因素为本振误差，影响距离误差的主要因素为位置误差。

2 影响因素理论分析

2.1 本振误差的影响

分布式干扰系统各节点通过独立的本振产生所需的载波信号，各本振输出信号的初始相位为随机值，且存在相位起伏。本振的输出信号可以表示为：

V(t)=V0sin(2π(f0+Δf)t+φ0+φn(t))

(12)

式中:V(t)为信号瞬时电压；V0为电压的幅值；f0为信号的标称频率；Δf为实际载波频率与标称频率的偏差，表征本振输出信号的频率准确度；φ0为信号的初始相位；φn(t)为信号的相位起伏，表征本振输出信号的频率稳定度。

相位起伏通常用频域的功率谱密度来表征：

(13)

式中：α为幂指数，其取值范围为0，-1，-2，-3和-4，分别对应5种独立的噪声过程：调相白噪声、调相闪烁噪声、调频白噪声、调频闪烁噪声以及调频随机游走噪声。

可见，基于初始相位、频率偏移和相位噪声的影响，本振输出信号会产生偏移，由此引起的相位误差为：

Δφ=2πΔft+φ0+φn(t)

(14)

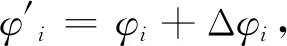
(15)

假设Δφi在[-Δφ,Δφ]上服从均匀分布，可以得到：

(16)

可见，相位误差的存在，导致分布式波束形成的性能下降，当相位误差为45°时，分布式波束形成的功率几乎下降一半。

2.2 位置误差的影响

位置误差对导致分布式干扰波束形成系统的影响体现在各节点的相位不同步。为方便讨论，假设各节点本振完全相同，不存在误差。

假设节点i的位置误差为(Δxi,Δyi,Δzi)，则分布式干扰波束形成系统的场强方向图如下：

F′(θ,φ)=

(17)

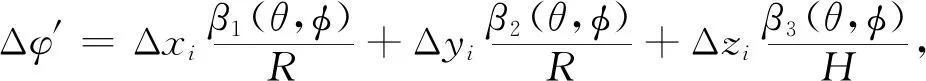
(18)

对应的归一化功率方向图为：

(19)

显然，上式和式(16)具有相同的形式，说明位置误差对分布式干扰波束形成系统性能的影响和相位误差具有等效性。

3 数值仿真

分别从方向性、节点空间分布及相位误差3个方面对分布式干扰波束形成系统的性能进行仿真。假设节点数N=20，节点均匀分布在底面半径为R、高为2H的圆柱区域内，由于位置误差和相位误差具有等效性，因此不再单独对位置误差相对分布式干扰波束形成性能的影响进行仿真。

(1) 干扰节点数量对归一化平均功率方向图的影响

图2给出了干扰节点的数量分别为10，30，50和70等不同情况下的分布式干扰波束形成系统归一化平均功率方向图，可以看出：干扰节点的数量越多，归一化平均方向图的主副比越大，即波束的能量越集中，波束形成的效果越好，但是系统也越复杂，进行系统同步所需的资源也越多。

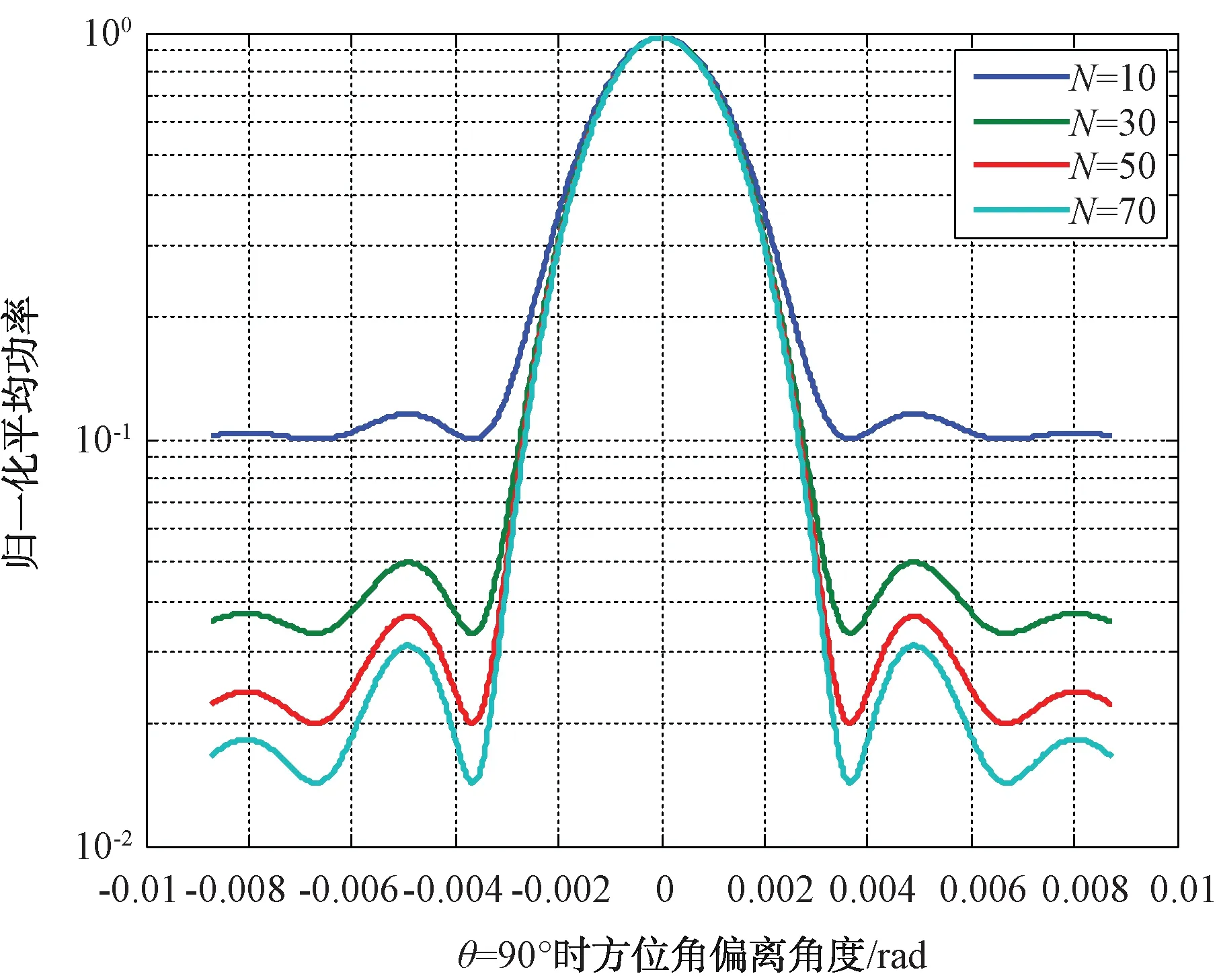
图2 不同干扰节点数量下的归一化平均功率方向图

(2) 干扰节点分布区域对归一化平均功率方向图的影响

相位误差Δφ取为10°，圆柱高度H取5 m，分别对R=50 m，100 m和200 m 3种情况进行仿真。仿真结果如图3所示。

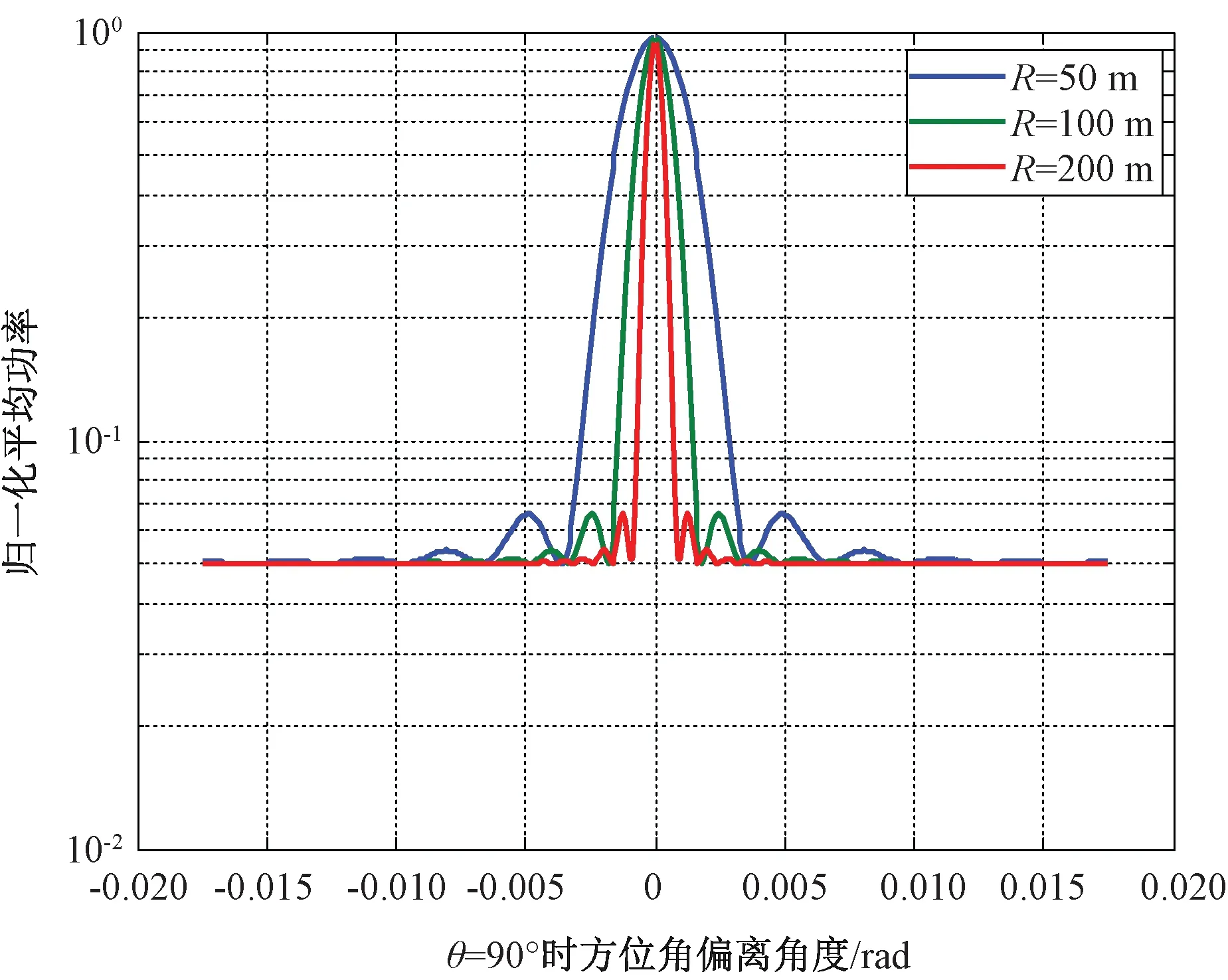
图3 不同R值下的归一化平均功率方向图

从图3可以看出，由于干扰节点的分布区域较大，分布式系统所形成波束的宽度极窄，R=50 m时，波束宽度仅为0.18°，且R越大，波束宽度越窄。这对于分布式干扰系统是极为不利的，因为波束指向的略微误差就会导致干扰波束偏离辐射源目标。为了获得理想的波束宽度，需要对归一化平均功率方向图进行综合；同时应该注意的是，归一化平均功率方向图的副瓣电平基本保持不变，但是干扰节点的分布区域越大，副瓣越向主波束靠拢，干扰能量越集中。

(3) 相位误差的影响

R取50 m，H取5 m，相位误差Δφ取值分别为0°，30°，45°以及60°，归一化功率方向图如图4所示。

图4 不同相位误差情况下的归一化平均功率方向图

可以看出，相位误差越大，分布式干扰系统的归一化平均功率的峰值越低，即分布式系统的波束形成效果越差，当相位误差为60°时，归一化平均功率的峰值下降60%，同时副瓣电平也随着相位误差的增加而降低。因此，为了保证一定的波束形成效率，必须控制分布式干扰波束形成系统的相位误差在一定范围内。

4 结束语

本文分析了本振误差、位置误差对分布式干扰波束形成性能的影响，得到了对应的性能表达式，仿真分析了干扰节点数量、分布区域和相位误差对归一化平均功率方向图的影响，得出结论如下：

(1) 本振误差对分布式干扰波束形成性能的影响主要体现在：本振误差越大，归一化平均功率方向图的峰值越低，即波束形成的效率越低；相位误差对分布式干扰波束形成性能的影响和本振误差具有等效性。

(2) 分布式干扰节点数越多，归一化平均功率方向图的主副比越大；分布式干扰节点空间上越分散，归一化平均功率方向图的主瓣越窄，干扰波束的能量越集中。