增程式电动汽车动力系统参数匹配及控制策略优化

李永亮，黄 英，王 绪，郭 汾

(北京理工大学 机械与车辆学院，北京 100081)

新能源汽车实现纯电驱动的趋势不可逆转，汽车电动化正受到世界各国政府和企业的高度重视[1-2]，但是由于当前车用动力电池技术水平和充电基础设施的限制，纯电动汽车与燃油车相比，有着续驶里程短，成本高昂，充电时间过长的短板，无法满足人们的需求。为了解决“里程焦虑”，增程式电动汽车（Extended-Range Electric Vehicle，E-REV）作为混合动力汽车和纯电动汽车的一种过渡车型，既能实现清洁电能的利用，又能保证续驶里程，逐渐成为研究热点[3]。

增程式电动汽车动力系统结构主要由驱动电机、动力电池、增程系统（小功率发动机-发电机组）、主减速器以及差速器组成，各部件参数的合理匹配是整车开发和控制策略制定的必要基础，对于提高整车动力性能和续驶里程具有重要意义。文献[4]～[6]基于车辆动力学原理，对增程式电动汽车电机、电池和发动机的功率选取进行了数值计算和仿真研究，文献[7]从电机工作特性和汽车驱动特性的合理匹配出发，对E-REV动力系统的参数设计进行了分析，上述设计方法[4-7]多是沿用传统汽车匹配流程，参数选择缺乏对实际工况的考虑。

在对匹配参数仿真验证的过程中，增程式电动汽车控制策略的选取同样影响其性能优劣，常用的控制策略有基于规则的定点控制策略和功率跟随控制策略[8]以及包括神经网络控制、模糊控制等在内的智能控制策略。智能控制策略在燃油经济性方面优于基于规则的控制策略，但是基于规则的控制策略简单可行，在工程上应用较多。文献[9]根据不同的发动机功率，选取了不同的增程器控制策略，优化了整车空间布置和功率分布。文献[10]在有利于增程式发动机小型化的前提下，对比了4种不同的规则型控制策略在燃油经济性上的差异及原因，确定了最优曲线控制策略用于增程式电动汽车的优越性。文献[11]以E-REV为研究对象，利用模糊控制算法设计了以动力电池SOC和驱动电机需求功率为输入，增程系统功率为输出的能量管理策略，获得了较好的控制效果。对于模糊控制和规则型控制策略控制参数的制定方法，以上文献根据经验分析给出，这使控制效果具有一定的随机性，降低了控制策略的鲁棒性和整车性能。文献[12]引入遗传寻优算法，以发电机总发电量和燃油经济性为优化目标，对所提出的三点控制策略进行参数优化，优化后的控制效果明显提升。

综上所述，目前的研究在增程式动力系统参数匹配以及相关参数的优化制定过程中仍然存在一些对驾驶工况因素考虑不够、对控制策略的优化方法研究不足的问题。本文首先在Simulink-Cruise联合仿真平台上利用整车基本参数建立了动力系统初始模型，针对增程式电动汽车匹配问题，提出了结合典型工况统计分析的参数匹配方法和流程；然后根据整车动力性指标和续驶里程要求，对增程式电动汽车驱动电机、动力电池和增程系统的参数进行了系统的稳态匹配设计；紧接着对比分析了CD-CS型最优曲线功率跟随控制策略和定点控制策略在燃油经济性、增程系统效率以及动力电池平均充电电流等方面的控制效果，确定了CD-CS型最优曲线功率跟随控制策略更适合当前匹配参数。对于动力系统参数优化问题，本文对部件参数和控制参数解耦优化进行了说明，在纯电模式下，优化了主减速比，在增程模式下，采用了更易实现的粒子群寻优算法，对所采用的功率跟随控制策略的控制参数进行优化，给出了控制策略在指定工况下的最优控制参数，为增程式电动汽车基于规则的控制策略控制参数的制定提供一种方法，也为后续复杂控制策略的完善奠定基础。

1 E-REV动力系统建模

1.1 E-REV性能指标和基本参数

本研究是在某混合动力汽车已有基本参数的基础上进行，其整车质量、风阻系数等基本参数见表1，动力性和经济性等性能指标见表2。

表 1 整车基本参数

续表1

表 2 整车性能指标

1.2 基于Cruise 的整车模型

根据表1中的整车基本参数，在Cruise中建立整车仿真模型，建模的关键部分有驾驶员模型，电机模型，电池模型和发动机模型，相关参数采用初始值，并在后续匹配过程中不断修正。其中，驾驶员模型模拟驾驶员控制车辆跟随目标车速行驶的状态，根据车速偏差给出踏板信号，如式（1）所示：

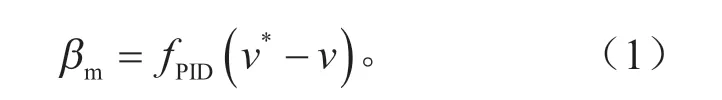
式中：βm为车辆踏板信号，βm＞0为驱动信号，βm＜0为制动信号；v*为目标车速；v为实际车速。

Cruise中驱动电机模型根据驾驶员给出的踏板信号、当前电机转速以及当前总线电压下的电机外特性转矩线查表得出电机的输出转矩，再结合电机转速和总线电压可求出电机效率和电机电流，如式（2）～（4）所示：

式中：Tm为电机查表转矩；Tm-out为电机输出转矩；ηm为电机效率；Im为电机电流；nm，Unet分别为电机转速和母线电压。

动力电池采用等效电路模型，母线电压由电池电压和电池电流计算，电池电压随电池SOC变化，电池内阻随电池的温度和SOC变化，具体计算如式（5）～（6）所示：

式中：UBatt为电池开路电压；IBatt，R，SOC分别为电池电流、电阻和荷电状态；Qimax为电池最大容量。

发动机在转速小于怠速转速时输出转矩为0，在转速大于怠速转速时输出转矩由发动机实际转速和节气门开度查表得到，发动机转矩输出模型如式（7）所示。发动机油耗的计算则是根据发动机功率和燃油质量流量计算得出，发动机油耗模型如式（8）所示。

式（7）中：Te为发动机输出转矩；Tf为发动机摩擦转矩；ne，nidle，αe，Te-max分别为发动机转速、怠速转速、节气门开度和峰值转矩。式（8）中：Q为发动机油耗，L；Pice为发动机功率，kW；be为燃油消耗率，g/kWh；ρfuel为燃油密度，kg/L。

2 E-REV动力系统参数匹配

2.1 驱动电机匹配

2.1.1 驱动电机的峰值功率

驱动电机的峰值功率由整车的性能指标确定，峰值功率应该达到最高车速vmax、最大爬坡度αmax及百公里加速时间ta分别对应的最大功率需求Pm1，Pm2，Pm3，下面对上述3个功率需求进行计算分析，如式（9）～（11）所示：

式（9）中：g为重力加速度，g=9.8 m/s2。式（10）中：vp为增程式电动汽车爬坡车速αmax为增程式电动汽车最大爬坡度，。式（11）中：ta为0-100 km/h加速时间，由于电机的工作特性，所以加速时间为恒转矩加速时间和恒功率加速时间之和，取基速处车速vb=45 km/h。式（12）表示不同车速时驱动力Ft的大小，将其代入式（11）便可得到ta和Pm3的关系。

将相关参数代入式（9）～（12），分别计算得到如图1所示的最高车速-峰值功率曲线、最大爬坡度-峰值功率曲线以及0-100 km/h加速时间-峰值功率曲线。

图 1 动力性与驱动电机峰值功率

由图1可知，要满足表2中的整车动力性指标，则驱动电机峰值功率Pm1≥36.13 km，Pm2≥38.43 kW，Pm3≥84 kW。驱动电机的峰值功率满足：

因此，匹配一台峰值功率为90 kW的驱动电机为宜。

2.1.2 驱动电机的额定功率和额定转速

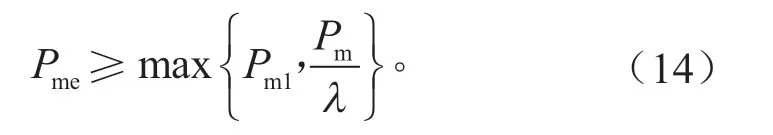
式中：Pme为驱动电机的额定功率；λ为电机的过载系数，按照过载系数1.8进行功率匹配，可得电机的额定功率为Pme=50 kW。

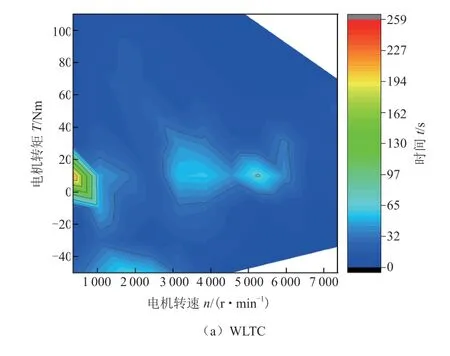
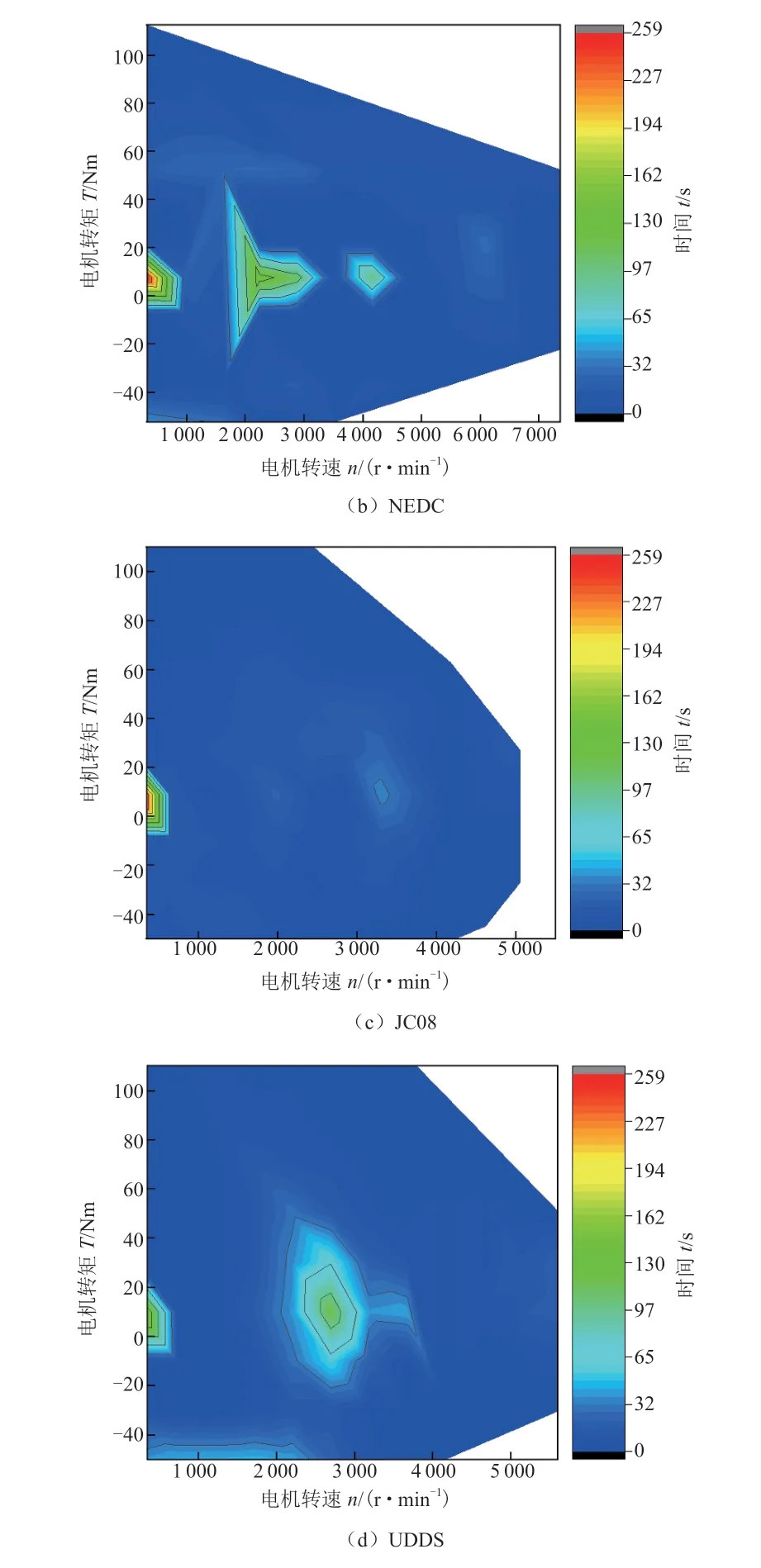
图 2 各工况电机工作点时间分布图

对于额定转速的选择，文献[13]提出通过分析驾驶员习惯的增程式电动汽车匹配方法，相比传统方法有所改进，但是对于驾驶员习惯的统计数据量庞大，且难以保证数据的准确性。因此，本文基于4种确定的典型循环工况（NEDC、WLTC、UDDS、JC08）在Avl-Cruise中计算出驱动电机运行工作点的工作时间分布，如图2所示，横轴为电机转速（r /min），纵轴为电机转矩（N），图中等线为对应工作点的工作时间（s）。由图可知，驱动电机大部分工作点都分布在2 500～3 500 r/min之间，而电机在额定转速附近效率最高，因此，以电机工作高频区和高效区重合为原则，综合考虑给定驱动电机的额定转nme为3 000 r/min。

2.1.3 驱动电机最高转速

将相关参数代入式中，求解计算得电机最高转速为8 906 r/min，取整为9 000 r/min。

最终确定驱动电机的基本参数，见表3。

2.2 动力电池匹配

2.2.1 电压匹配

电池电压的匹配原则是在满足峰值功率和附件功率需求的情况下，电池电压不低于额定电压的要求。

式中：UBat为电池电压；PAc为附件功率；Pm为驱动电机峰值功率；Um为驱动电机额定电压；R为电池内阻。代入前文驱动电机匹配参数，得到UBat≥345.34 V。参考GB/T18488.1—2015中有关电源电压等级的规定，选择动力电池的额定电压UBat=350 V。

2.2.2 功率匹配

电池功率匹配的原则是电池额定功率满足电机和附件的功率需求，以保证纯电模式下的整车性能。

等价于：

式中：k为电池的最大放电倍率；Cp为功率要求的电池容量；ηMc为电机和电机控制器的平均效率，ηMc=0.92，其余参数见表1和表2 。

2.2.3 能量匹配

电池能量的匹配原则是电池总能量需要满足整车的纯电续驶里程，根据GB/T18386—2017中的规定，应用90 km/h等速法进行电动汽车续驶里程试验，动力电池的总能量满足纯电动续驶里程d1的能量要求，即：

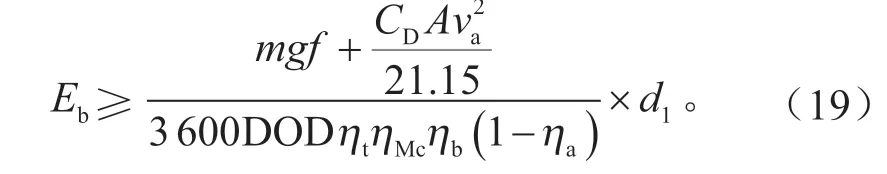
等价于：

式中：CE表示能量要求下的动力电池容量；DOD为动力电池的放电深度，DOD=0.8；ηb为动力电池的平均放电效率，ηb=0.95；ηa为汽车附件能量消耗比例系数，ηa=0.008；其余参数见表1和表2。将相关参数代入式（16）～（19），可得图3所示的动力电池最大放电倍率-安时容量曲线。

动力电池容量Cb按下式进行选取：

图 3 电池最大放电率-安时容量曲线

由式（21）得到图3中的点2，对应动力电池容量为42.386 Ah，最大放电率为6.6 h-1。但考虑到E-REV动力电池容量较大，实际车用电池的最大放电倍率范围通常不超过5 h-1，选择点1处最大放电倍率为5 h-1，容量为56 Ah更为合理。

最终确定动力电池的主要参数见表4。

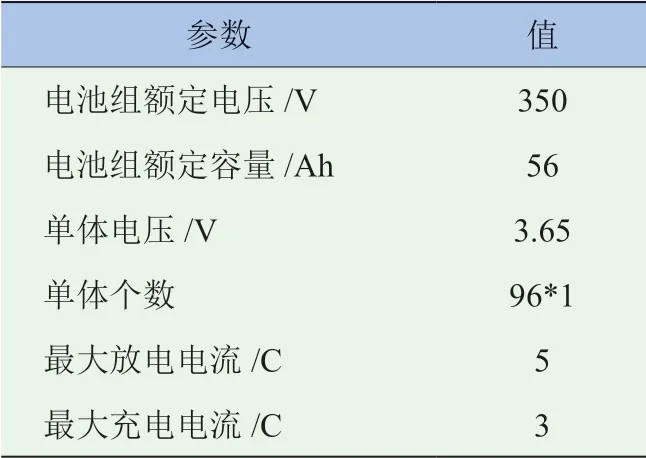
表 4 磷酸铁锂电池(LiFePO4)电池参数

2.3 增程系统匹配

增程系统由发动机、发电机及其控制器组成，发动机和发电机串联耦合，其参数匹配决定了整车的续驶里程长短和燃油经济性好坏。

2.3.1 发动机功率匹配

发动机的功率匹配原则是在增程模式下发动机输出功率满足驱动电机和附件的功率要求，同时兼顾发动机效率，即典型城市工况或常用巡航车速时的功率需求与发动机高效工作区域尽量重合，式（22）为等速巡航时发动机的功率计算。

式中：ηMc为驱动电机及其控制器的平均效率，ηMc=0 0.92；ηg为发电机及其控制器的平均效率，ηg=0.92；va为等速巡航时的车速，取va=90 km/h，代入参数计算得

此外，考虑到典型城市工况对整车功率匹配的影响，增程系统需要满足大多数行驶工况下的动力性要求。基于整车基本参数对增程式电动汽车在各行驶工况下的整车需求功率进行统计分析，利用AVL-Cruise计算得到NEDC、WLTC、JC08、UDDS工况下整车需求功率及区间分布如图（4）～（5）所示。

图 4 NEDC、WLTC、JC08和UDDS工况整车需求功率

由图可知，4种典型工况下整车需求功率大部分时间都小于60 kW，功率需求集中于0～20 kW，占比达到了0.7左右。WLTC工况的峰值功率最大，为63 kW，JC08工况的峰值功率最小，为25 kW。WLTC工况下整车平均需求功率达到了17.23 kW，其余典型工况的平均需求功率均小于此值。

图 5 各工况整车需求功率区间分布

由于增程式电动汽车发动机驱动功率不需要满足整车的峰值功率需求，所以允许选择较小的发动机，其功率只需满足增程模式下指定工况的持续功率需求。以WLTC工况的平均需求功率为计算标准，根据式（22）～（24）计算得到发动机常用工作点功率需求

2.3.2 发电机匹配

发电机参数匹配时，需要综合考虑发动机和发电机间的总体动力传递方式，本文中发动机与发电机同轴连接构成一体化结构，发电机与发动机的工作转速及机械输出功率等应尽可能保持一致，以满足工作平顺性要求。发电机额定输出功率应和发动机高效区相匹配，由此计算发电机额定功率为

根据匹配计算的各部件相关参数选择合理的试验数据对动力系统模型进行完善和修正，为了保证发动机效率，实际选择的发动机高效区功率至少需要大于前文计算得到的常用工作点功率，过小的功率选择会使发动机长期处于高负荷状态，效率降低，过大的功率选择会对整车成本和布置安装空间有影响，合适的发动机功率选择有助于整车综合性能的提升。本文选择的发动机和发电机功率较匹配计算值偏大，在增程模式下能够提供充足的充电功率，对于发动机效率和动力电池寿命等关键因素的影响可通过控制策略的合理设计达到较优水平，选择的驱动电机效率、发电机效率以及发动机万有特性曲线如图6所示，其中发动机在160 Nm，2 500 r/min时比油耗最低，为216.5 g·kWh。

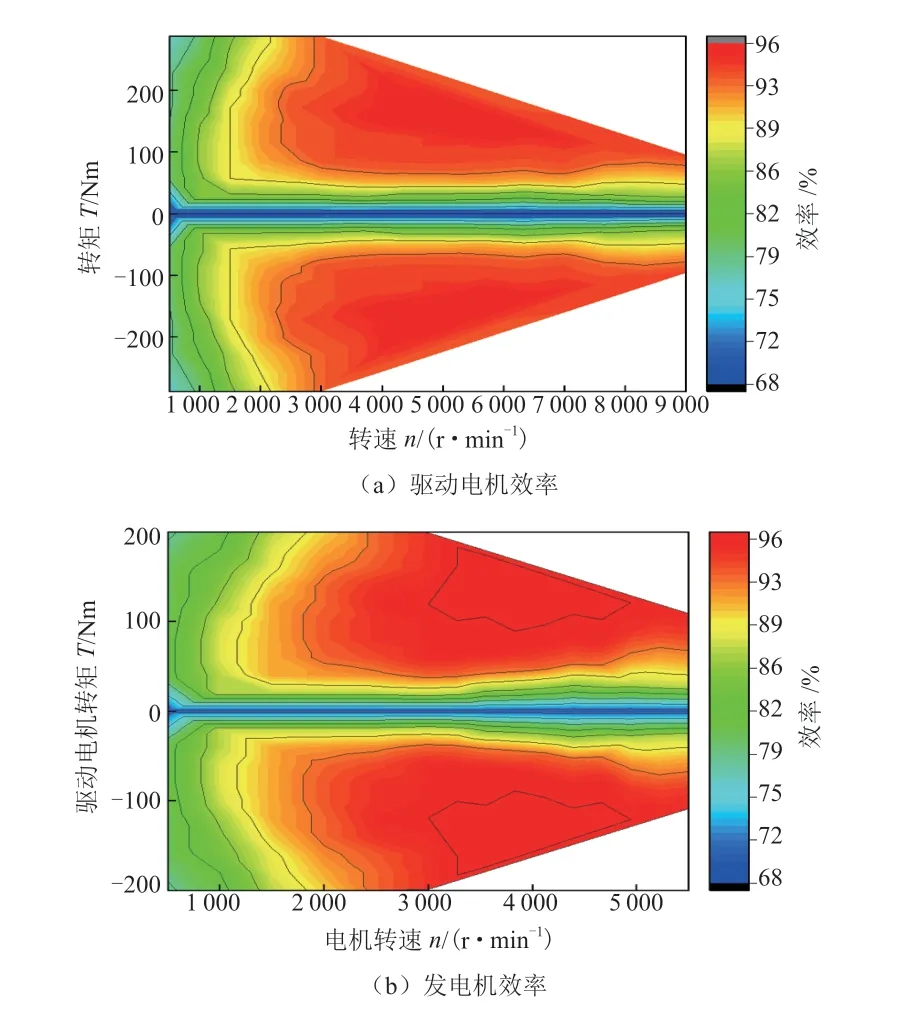
图 6 电机和发动机试验数据

2.4 动力性验证

增程式电动汽车动力性仿真结果如图7所示，仿真结果表明车速为25 km/h时，最大爬坡度为38.14%，0-100 km/h的加速时间为11.05 s，最高车速为141.51 km/h，满足增程式电动汽车动力性能指标，表明驱动电机参数匹配合理。

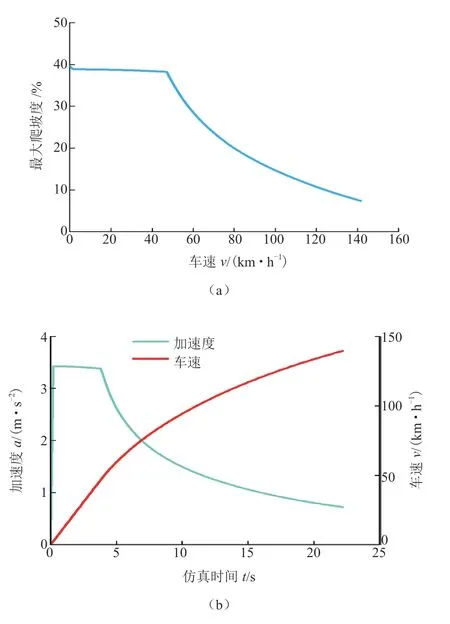
图 7 动力性仿真结果

3 控制策略设计

由于动力电池容量充足，且整车动力性与发动机机械解耦，为了达到更好的燃油经济性和排放性，E-REV控制策略区别于传统发动机控制，可以使发动机持续工作在其高效区域，常用的方法有基于规则的恒温式定点控制策略和功率跟随控制策略。恒温式定点控制策略根据动力电池SOC控制发动机的启停，使发动机一直工作在其效率最高点，输出功率恒定且不随驱动电机需求功率而改变，SOC变化为CD-CS型。功率跟随控制策略则是根据需求功率的不同随时改变发动机的工作点，以使增程系统输出功率跟随整车需求功率，发动机工作点分布于增程系统效率最优曲线上某一连续范围，或者该曲线上多个固定的功率输出点上[12，14]，动力电池SOC变化可以为CD-CS型，也可以为BL型[15]。

3.1 CD-CS型最优曲线功率跟随策略

为了进一步验证匹配参数在增程模式下的合理性，并且简化计算过程，采用CD-CS型功率跟随控制策略作为增程系统控制策略。其控制逻辑如图8所示，当动力电池SOC处于高位时，执行CD模式，整车需求功率Preq由动力电池提供，增程系统输出功率PAPU=0；当电池SOC低于SOC下限值或者需求功率高于电池额定放电功率Pbatt时，进入CS模式，此时增程系统开启，发动机工作在增程系统效率最优曲线上，发动机输出功率在一定范围内跟随整车需求功率。

图 8 功率跟随控制策略

3.2 控制策略仿真分析

动力电池SOC初始值越高，则E-REV纯电续驶里程越长。为了便于研究增程模式下的整车性能，可将初始SOC值设定为一个相对较低值，而SOC上限值一般由具体策略决定，下限值则是由电池本身特性决定，当电池SOC过低，电池内阻会急剧增加，降低电池放电效率， 所以SOC下限值不应低于某一特定值。根据本文得到的电池特性数据，仿真中设置SOC初始值为0.6，设置控制参数SOC上限值为0.4，下限值为0.3，由发动机万有特性设置功率跟随上限值为60 kW，下限值为10 kW，在WLTC工况下进行仿真，以确定前文匹配参数是否符合实际工况要求。

仿真结果如图9所示。由图9a和d可知，仿真初期，随着工况车速变化，整车需求功率消耗由动力电池提供，电池电量不断减少，当SOC到达SOC下限0.3后，增程系统开启，发动机-发电机组输出功率，跟随整车需求功率，使电池SOC在0.3～0.4间规律波动。从图9b局部SOC变化可以看出CD-CS型最优曲线功率跟随控制策略使动力电池SOC在增程模式下变化缓慢，有效地避免了电池充电和放电过程的频繁切换。母线电流变化曲线如图9c所示，动力电池最大充电电流为72.71 A，不超过3 C，最大放电电流为172.05 A，不超过5 C，符合匹配设计的电池工作特性，发动机工作点分布如图9e所示，保证了整车综合效率。与定点控制策略相比，如表5所示，CD-CS型最优曲线控制策略由于发动机转速变化，虽然在各个转速点效率最优，但是总体效率略差，使得燃油经济性不如定点控制策略，但在此控制策略下平均充电电流降低了40.46%，在目标工况发动机启停次数减少了50%，说明CD-CS型最优曲线功率跟随控制策略更适合当前整车设计参数。

图 9 五个WLTC工况仿真结果

表 5 与定点控制策略对比

4 E-REV动力系统参数优化

增程式电动汽车的参数优化是多目标非线性优化问题，影响因素众多。本文在稳态匹配的基础上，结合试验数据，使电机和发动机的参数得以确定，缩小了优化范围，主要对部件参数主减速比和相关控制参数进行优化。

4.1 主减速比优化

增程式电动汽车传动系统对整车动力性能影响较大，主减速比i0的大小决定了整车动力性和驱动电机工作效率，因此，首先对主减速比进行优化。

由于增程式电动汽车前后功率链没有机械耦合，对于主减速比的优化可以单独考虑。以纯电模式下驱动电机电耗作为评价指标，主减速比在其可取范围内满足动力性指标即可。

主减速比上限由电机最高转速和最高车速决定，下限由车辆的最大爬坡度和电机的最大转矩确定：

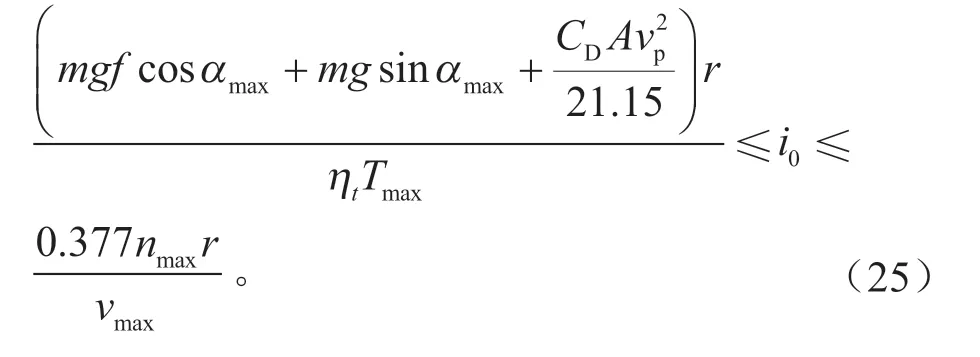
在该范围内设置控制参数与上节相同，在单个WLTC和NEDC工况下的仿真结果如图10所示。

图 10 电耗随主减速比i变化曲线

随着主减速比的增加，在目标工况下的耗电逐渐增加，最大爬坡度也逐渐增加，100 km/h加速时间逐渐减少，在符合动力性的情况下，主减速比为6.2时，驱动电机电耗最少，所以取最佳的主减速比为6.2。

4.2 控制参数优化

4.2.1 控制参数优化变量

CD-CS型功率跟随控制策略，SOC控制增程系统的启停且决定了动力电池的工作效率，当SOC低于下限值时，电池效率降低，无法输出额定功率，而SOC上限值决定了电池放电水平并影响增程系统的启停次数，所以将SOC上下限值SOCmax和SOCmax作为优化变量。功率跟随范围决定了发动机输出功率大小，进而影响发动机油耗，因此，可以将功率跟随上下限值Pmax和Pmin作为优化变量。综上所述，选取的优化变量为：

4.2.2 目标函数及约束方程

（1）目标函数

根据汽车实际用途选取目标函数，本文研究对象为增程式城市SUV，对整车经济性和舒适性有较高要求，并且控制策略应该考虑电池寿命，因此，匹配优化的过程中以百公里综合油耗、发动机启停次数和平均充电电流为目标函数。

式中：J1为百公里综合油耗；Scycle为目标工况行驶里程；G为电耗转换为油耗的换算系数，以当前每kWh电价比上每升油价，取G=0.232；t0为工况开始时刻，tf为工况结束时刻；I为电池电流；U为电池电压；Cb为动力电池容量；q为燃油质量流量；ρfuel为燃油密度。

发动机的频繁启停会严重影响整车舒适性和排放，因此，将发动机启停次数也作为目标函数。

式中：Neng_switch为目标工况下发动机的启停次数。

电池充电电流的大小会影响电池寿命，所以将充电电流的平均大小列为第3个指标：

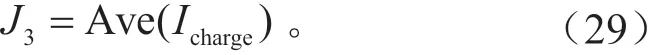
式中：Ave（Icharge）为目标工况电池的平均充电电流。

（2）确定约束方程

SOCmin是一个相对的范围，超出此范围后电池内阻急剧增大，会导致效率大幅降低，根据本文已选动力电池的固有特性，最终确定下限值范围为0.15～0.4。SOCmax应使电能较多地被利用，同时不会导致APU频繁启停，可取范围为0.2～0.5且大于SOCmin。

对于功率跟随控制策略，功率跟随范围应包括发动机高效区功率，具有一定的功率可调范围，并且避免让发动机工作在低负荷区，由前文各工况下整车需求功率初步确定范围：

动力电池充放电电流应符合电池工作特性，母线电压波动不超过额定电压的10%。

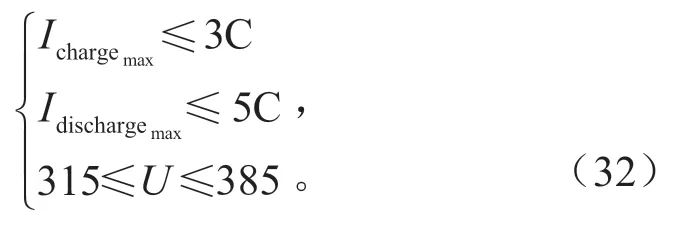
综上所述，利用加权法得到关于控制参数的优化目标函数和约束方程为：

式中：u，v，w为各目标的加权系数，取u=0.6，v=0.2，为各目标参考值为最大充电电流；g2(x)为最大放电电流；g3(x)为母线电压。

4.2.3 粒子群算法

粒子群算法是一种简单可行的进化算法，其灵感来自于鸟类、蚁类等动物种群的捕食行为，在整个搜寻的过程中，通过相互传递各自的信息，判断是否找到最优解，同时也将最优解的信息传递给整个种群，最终实现问题收敛[16]。控制参数优化时粒子群算法的计算流程如图11所示。

图 11 粒子群算法计算流程

本文中粒子的初始位置和速度定义为：

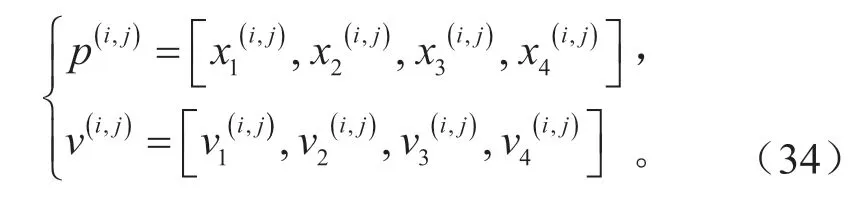
式中：i代表粒子序号，i=[1,2,3,…,m]；j代表算法迭代次数，j=[1,2,3,…,N]。在每次迭代找到个体极值和群体极值后，粒子位置和速度更新遵循下式：

式中：ω为惯性常数；β和γ为加速常数；rand()*为0～1的随机数。本文中种群粒子数m=10，迭代次数N=40，ω=0.8，β=0.9，γ=0.9。

4.2.4 优化结果分析

选取的优化工况仍为5个WLTC，控制策略为CD-CS型最优曲线功率跟随控制策略，由于动力电池初始值会影响车辆进入增程模式的时刻，所以设置动力电池SOC初始值和前文一致为0.6。图12为优化过程中4个控制参数和优化目标之间的二维散点图。

图 12 优化变量和目标函数变化

其中最优粒子的4个控制参数和目标函数随迭代次数的变化如图13所示，由图可知，目标函数最终仍在一定范围内波动，这是由于多目标优化问题的解不可能是某单一解，而是一组满足约束条件的非劣解即Pareto最优解集。选取图中标出位置为最优择衷解，优化前后SOC随车速变化对比如图14所示，优化前后性能对比见表6。

图 13 控制参数随迭代次数的变化

图 14 优化前后SOC变化曲线

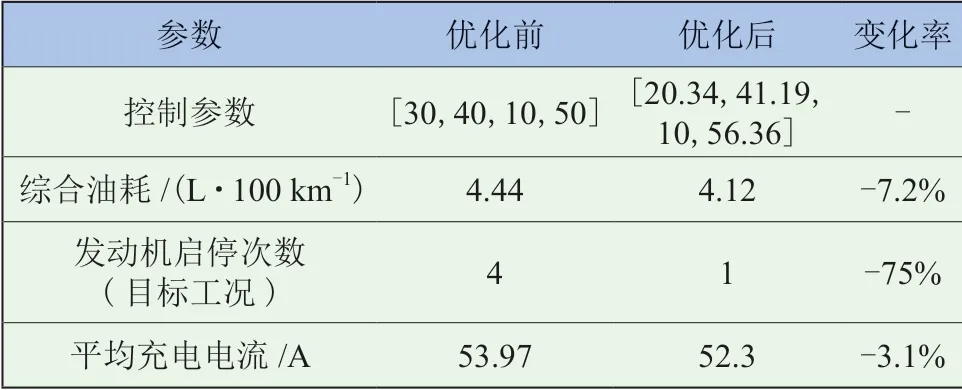
表 6 优化前后性能对比

优化后的控制参数使整车百公里油耗下降了7.2%，发动机在目标工况下的启停次数减少了3次，平均充电电流减少了3.1%，对于整车节能减排和电池寿命的延长具有重要意义。为了找到各个控制参数对于目标函数J的影响规律，将仿真得到的粒子位置线性拟合，得到控制参数对于目标函数的全局影响因子，如图15所示。由图可知，SOCmax对于目标函数的影响最大，在允许范围内SOCmax越大，目标函数J越小；SOCmin和Pmin对于目标函数的影响次之，且与目标函数J正相关；Pmax的影响因子最小，其值越大，目标函数J越小。

图15 控制参数对目标函数的全局影响因子

5 结论

（1）针对增程式电动汽车参数匹配问题，在Matlab/Simulink和Cruise联合仿真平台上搭建了整车准稳态模型，根据整车基本参数和性能设计指标，完成了增程式电动汽车动力系统的选型和匹配，提出了基于典型工况统计分析的增程式电动汽车参数设计方法，该方法考虑了实际工况特征对于整车匹配的影响，使整车参数设计具有一定的工况适应性。

（2）采用CD-CS型最优曲线功率跟随控制策略和定点控制策略分别对匹配参数进行验证，对比分析了两种控制策略在燃油经济性、增程系统效率和动力电池平均电流等方面的控制效果，确定了CD-CS型最优曲线控制策略更适用于当前匹配参数。

（3）通过纯电模式的仿真完成了部件参数主减速比的优化，并提出了表征E-REV动力系统综合性能的目标函数。在此目标函数下，基于粒子群算法对CD-CS型最优曲线功率跟随控制策略的控制参数进行了优化求解，优化后的参数使整车燃油经济性提升7.2%，发动机启停次数大幅减少，平均充电电流降低了3.1%，该优化方法为增程式电动汽车规则型控制策略控制参数的制定提供了理论参考。

（4）由于基于规则的控制参数会随着工况特征和行驶里程发生变化，针对不同的行驶工况和行驶里程以及不同的控制策略的优化是下一步的研究重点。