基于遗传算法的共架发射系统武器空域协调方法
2021-06-15徐宁
徐 宁
(江苏自动化研究所,江苏 连云港 222061)
新形势下,共架发射可为舰载武器系统全方位作战创造更优、更安全、多武器通用的发射平台,对水面的舰艇攻击、防御和生存等综合作战能力起到重要作用[1]。舰载导弹垂直发射装置逐步向通用化、系列化、模块化、小型化发展[2]。这种情况下,对多种类型弹药在共架发射时的弹位选取策略和发射协调问题就显得尤为重要。合理的发射策略能提高决策效率,增强总体的火力密度。
1 发射选取原则
当进行空域协调决策时,要遵循以下原则:
1)筛选所需要的弹种
舰载垂直共架发射系统往往需要装备多种导弹以对付不同发射目标,因此当前形势下,多弹种、大载弹量是共架发射系统的发展需求。这就使得在空域决策时,弹药种类的选择被置于最高优先级。
2)不选择与上次发射相邻的隔舱,且距离上一次发射隔舱尽量远
公共燃气排导结构的共架发射系统,以美国MK41为代表,八个隔舱共用一个排导通道[2],沿舰首尾线对称分布。武器发射时,发动机排出的燃气流速度高、排量大,产生的突加载荷以压力波的方式通过弹体传播,使整个导弹及其内部元件产生径向和横向振动响应,对周围的隔舱和未点火的导弹产生影响[3]。选取距离较远的弹药能有效减少多武器发射的相互影响。
3)发射弹药尽量选在不同模块,且保持中轴线两侧对称分布
当某隔舱内的武器发射后,隔舱盖处于开启状态时,同模块的其他弹药就不能进入点火程序,需要等到该弹药离架且隔舱盖关闭为止[4]。同一模块的发射应该保证一定的时间间隔。并且,弹药的选取应均匀分布在中轴线两侧,不会对船舱左右两舷的平衡造成影响。
4)尽量选取初始弹道不交叉的弹药
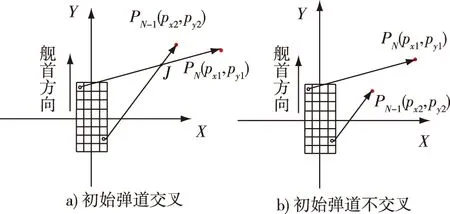
当弹药发射升空后,初始弹道的方向由武器发射位置和攻击目标所确定,飞行弹道一般是空间三维状态,为了简化计算,一般判断在一定时间区间内其初始弹道在水平面上的投影是否交叉[5]。当必须选择初始弹道交叉的导弹发射时,当前导弹的点火时刻需要在结合时域协调的基础上延迟一个适当的时间[6]。本文仅针对空域协调展开。
2 模型建立
2.1 共架发射系统数学模型


图1 共架发射系统模型
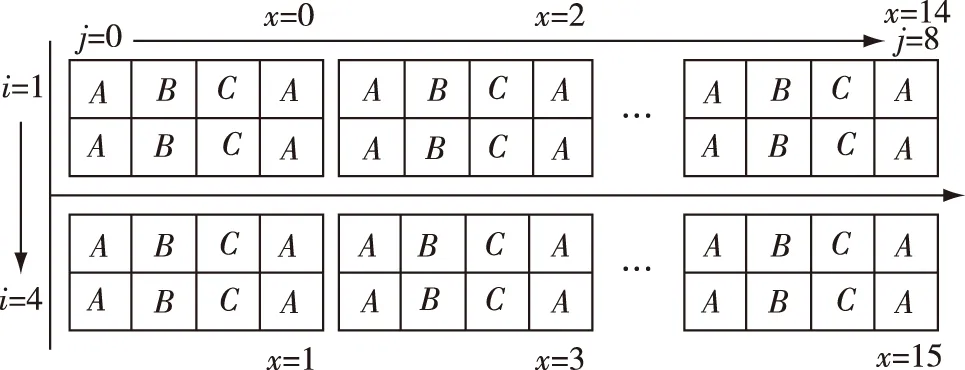
本算例基于三种弹药型号建立模型,可以用矩阵 简化系统的武器布局,分别用1、2、3代表A、B、C三种类型的弹药。每一个单元都可以使用一个坐标表示,c1,4=1表示模型中第1行第4列的弹药类型为A,如式(1)所示。模块分配可以用式(2)描述。
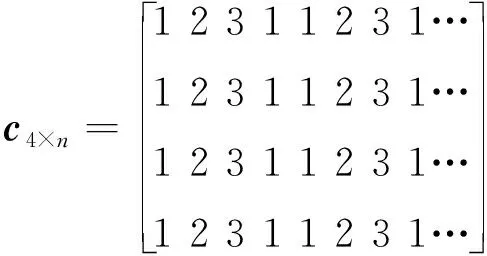
(1)
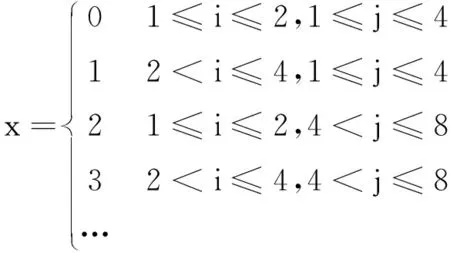
(2)
2.2 染色体编码
使用遗传算法求解该问题时,考虑采用二进制编码的方法,特定的位数指代每个隔舱个体单元的位置属性。选择7位时,第1—4位表示所在模块,第5、6位表示个体位于每个模块内的列位置,第7位表示个体位于每个模块内的行位置。七位二进制编码染色体的基因型有128种,可以不重复地表示128个位置。例如图2所示,基因型表示模块2中第二行第四列,即c2,8。这种编码方式具有很好的拓展性,对于体量更庞大的系统,扩展二进制位数并赋予对应编码意义即可。解码工作只需简单的函数即可完成。

图2 二进制编码示例
2.3 适应度函数构建
适应度函数依据目标函数的值,将个体的表现通过数值评价表现出来。适应度函数在构建时,要综合考虑第一节罗列出的四个原则,这是一个有约束的多目标优化问题。上述选取原则在解的选取方面并无冲突,在本算例的适应度函数构建中,通过在各个目标之间进行协调权衡和折中处理的方式,调整权重转化为单目标优化问题。
定义对于二进制编码个体Xk的适应度函数为Fit(Xk)=δ(f(Xk)),其中,f(Xk)为优化问题的目标函数,δ(f(Xk))是适应度变换函数,将目标函数转化为适应度函数,这里要求适应度函数Fit(Xk)是以目标函数f(Xk)为变量的函数[7],本算例中,目标函数值越小的个体具有越大的适应度函数。
定义一个矩阵Done=[i,j,x,px,py]来记录导弹发射的历史数据,其中i,j,x表示已发射的导弹在模型中的行、列、模块位置描述矩阵,(px,py)表示导弹目标位置在相对于船体的坐标系中的横纵坐标矩阵。Done在每次发射选择完毕后更新发射记录,同时将上次发射位置的属性矩阵的对应位置0。
设当前对第N个发射任务进行弹药选取运算。nneed为某次所要发射的弹药类型。当对种群中的第k个个体,构建用于评估适应度的目标函数f(Xk)时,可以采用以下形式:
(3)
其中,D(k),M(k),S(k),jc(N)分别为距离、模块、弹药发射平衡性及路径交叉评估系数。
弹药的种类选择是共架发射空域协调问题中优先级最高的选取原则,由于在遗传算法中,初始化的种群是完全随机的,对类型不符合的几种进行的目标函数计算和适应度评估,对计算机来说是一种时间和性能的浪费。本算例对原始遗传算法加入“沉底”的改进,对非指定种类的个体的目标函数赋最大值,随着新一代群体的更迭,非所需种类的个体逐渐被淘汰。
考虑公共燃气排导结构的共架发射系统对弹药选择的条件制约,c(i,j)=nneed时的目标函数f(Xk)中,结合了评估系数D(k),M(k),S(k)和评估函数jc(N)。评估系数的选取原则如表1所示。

表1 评估系数选取原则表
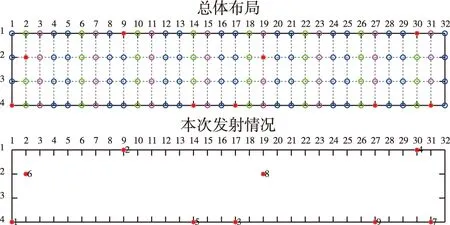
S(k)是用于调节发射平衡性的评估系数,s1>0,s3 M(k)是关于模块选取的评估系数,m0=1>m3>m2>m1>0。在选取弹药时,通常更青睐于模块之间的均匀选择,一方面可以方便于单个模块内部控制管理,另一方面也可以有效减少共架发射时的相互干扰。在本算例中,调取第N-1至N-4次的模块记录,通过常系数M的选取,尽量筛选与前几次发射模块不同的模块。 D(k)是用于评估弹药距离的系数。 iN-1,jN-1,xN-1表示上一次发射弹药的行位置、列位置和模块编号。 ik,jk,xk表示种群中第k个个体的行位置、列位置和模块编号。 将弹道投影到二维平面后,飞行弹道交叉的问题就变成了判断轨迹线段在二维坐标系下是否有交点,如图3。 图3 初始弹道二维坐标系 评估函数如下 (4) 其中,种群第k个个体若瞄准目标方位PN,依次与第N-1至N-3枚弹药的发射轨迹做交叉判断,若无交叉,Jk,i=0,若有交叉,按照与第N-1至N-3枚交叉的顺序,依次取值J1,J2,J3,其中,J1>J2>J3。 随着代数的逐渐增加,种群的个体逐渐收敛于局部最优解,这就使得算法的寻优能力下降。对评估系数引入自适应因子g。 其中fnmin、fnavg、fnmax分别代表第n代种群个体的最小值、均值和最大值。 通过对比选取结果的优劣,令: (5) (6) j′=j-k2·d2 (7) 当群体适应度趋向集中、多样性差时,g的值就会减小。当g小于某一阈值时,自适应改进的评估系数会动态变化,拉开优势个体与次优个体间的差异,保证最优解的突出。 当N=1时,即首个发射的导弹,其选取仅需考虑目标方向就近模块优先发射。 当船舱里的弹药储备量逐渐减少,或是弹药装备数量少且集中于同一模块时,对应染色体种群内个体的差异性就越来越小,不利于遗传算法选取最优解。针对这种特殊情况,需要增加对目标函数值作局部调整的模块,筛选出有潜力的个体。 种群个体的选择操作通过轮盘赌的方法进行,每个个体进入下一代的概率等于它的适应度值与整个种群中个体适应度值和的比例,适应度函数越大的个体越有可能保留下来。 交叉操纵是遗传算法中重要的一步,通过交叉操作可以得到新一代的个体,交叉是种群信息交换的重要途径。本算例采用单点交叉的方式,在个体染色体串中只随机设置一个交叉点,然后在该点相互交换两个配对个体的部分染色体。 对于二进制编码方式,变异操作在种群中随机选择个体,以一定的概率pm随机地改变染色体结构数据中的某个基因值以形成新的个体。类似于生物界,变异的概率一般取得较小。变异结果有好有坏,能防止算法陷入局部最优解。 算法的总体流程图如图4所示。当算法判定为不是第一枚弹药时,将进入遗传算法选择弹药流程。由于遗传算法模拟生物进化模型,需要人为设置最大迭代次数,每次迭代进行选择、交叉、变异,直到达到设定迭代次数,选取最优解作为本次选弹结果。 图4 算法流程图 假设执行某次发射任务的共架发射系统含16模块,128弹位,装备有A,B,C三种弹药。一次发射指令的下发是分别输入所需A,B,C弹药的数目和每个弹药的目标坐标。 本算例中算法的相关参数和评估系数选取如表2和表3所示: 表2 评估系数选取 表3 遗传算法参数选取 采用分散布局形式进行算例验证,其示意图如图5所示。 图5 128弹位共架发射系统的分散布局示意图 基于以上四项选取原则,建立了一套百分制的综合发射评价指标,用于评价发射次序决策的优劣,表4和图6分别为某次发射任务的要求及选取结果。 表4 选取要求和选取结果 图6 总体布局及发射情况示意图 设某次发射任务要求一次性作出128颗弹药的发射次序决策,本算例用Matlab随机生成128个位置坐标信息,分别采用评估系数固定的遗传算法和评估系数自适应改进的遗传算法进行发射次序决策,对比算法改进前后的决策效果,详细发射次序如图7a)和b)所示。 表5 算法改进前后决策效果对比 图7 发射次序 由实验数据可知,改进后的算法复杂度增加,牺牲了部分计算时间,但算法的寻优能力增强,决策结果的评分均值提高,方差显著减小,说明改进后的算法相对改进前有更好的效果。 本文总结了共架发射系统空域协调问题的约束条件并归纳得到四条主要选取原则,并在这一基础上提出了采用二进制编码遗传算法求解的新方法。该方法的编码方式有较强的拓展性,考虑系统规模进一步扩大时,也能有较好的适用性。针对不同情况下对选取条件的优先级需求的不同,可以通过更改适应度函数中各项的评估系数来调整,这是一种比较实用,易于实现的空域协调决策方法。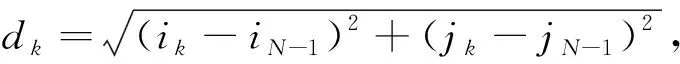

2.4 评估系数自适应改进


2.5 特殊情况的算例调整
2.6 选择、交叉与变异操作
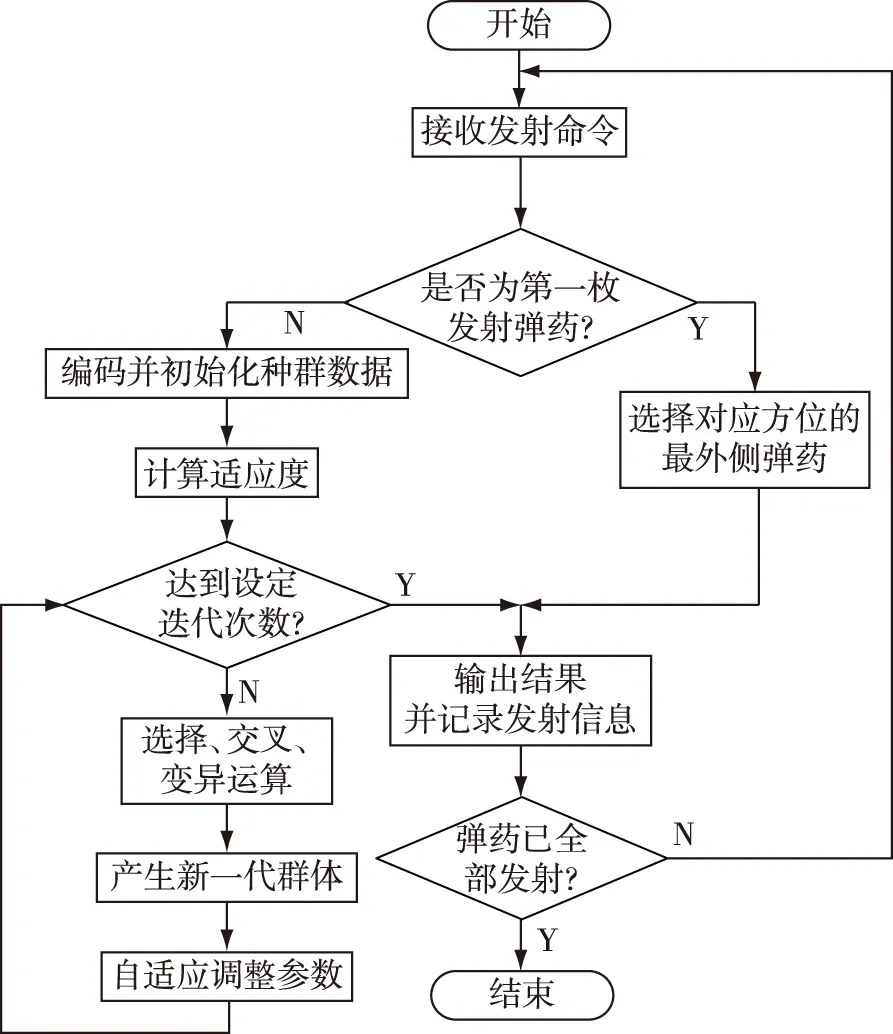
3 算例验证





4 结束语
