基于谱估计的方位时间序列匹配算法
2021-06-15郭昕钰张飞飞
郭昕钰,张飞飞,吕 收
(海军航空大学青岛校区,山东 青岛 266041)
20世纪70年代以来,随着军事作战理论的不断创新以及军事装备的不断发展,潜艇作为水下重要的武器平台,以高度的隐蔽性和机动性,成为难以捉摸的水下导弹发射场,更是成为战略核反击系统的重要平台,潜艇在未来海上作战中具有非常重要的战略作用。对潜探测技术是海上反潜作战的关键,伴随科学技术的飞速发展和军事强国海上作战能力的不断提升,为了及时侦测、打击、摧毁潜艇目标,世界海军强国竭力研发精准探测设备,并不断推进水下目标探测技术创新。纯方位目标运动分析只需要目标的方位序列信息,就可以估计出目标的距离、航向、航速等运动参数[1-2],从而一直被作为精确探测水下目标的重要研究手段之一。
纯方位目标运动分析作为一种无源探测定位方法,观察者在不需要向外发射信号的情况下,可利用目标自身的辐射声波,经过一系列严格的算法,完成对其定位,遂行军事作战任务。基于如此广泛的实用研究价值,学者对纯方位目标运动分析做了大量研究[3-9]。本文的主要工作是通过引入匹配场理论与谱估计理论来解决运动目标的运动参数估计难题。
首先,建立纯方位目标运动分析(Target Motion Analysis)的匹配场模型,依据匹配场模型获得拷贝场,选取合适的目标函数。其次,将目标函数引入相位中,转变为谱估计问题。本文运用子空间MUSIC算法和傅里叶变换法,对匹配场模型进行谱估计处理,设计仿真实验,比较两者的精确度及收敛时间等性能。
1 模型介绍
如图1所示,假设目标匀速直航,而观测平台(即本舰)进行一次机动。当目标进入被动声呐的观测区时,声呐将会记录下每一时刻目标的方位信息。目标的运动轨迹可由目标初始距离D0、初始方位F0、目标航速Vm以及航向Hm唯一确定。令初始时刻为t0(t0=0),观测平台在初始时刻的位置W0为坐标原点。y轴正方向为t0时刻由本舰指向目标的初始角度F0。令F0=0,ti时刻时,本舰的位置为Wi,此时的航向为Hwi,航速为Vwi,本舰指向目标的方位角为Fi。对本舰运动航向和航速的采样间隔为Δt。设本舰的总横位移和总纵位移分别为Jios和Jioc:
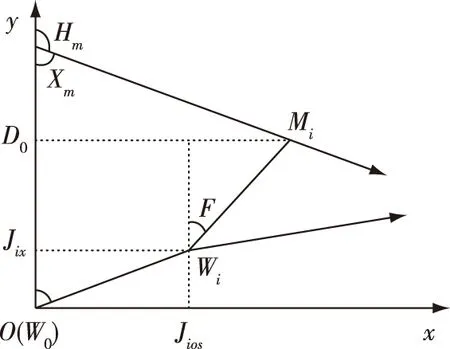
图1 观测平台和噪声目标之间的几何关系
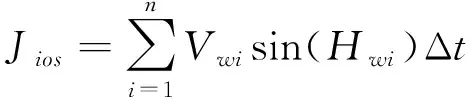
(1)
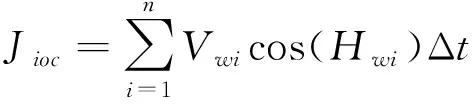
(2)
目标初始航向为Xm=180-Hm,则目标横向位移为VmsinXm×ti,目标纵向位移为VmcosXm×ti,则由图中所示几何关系可得
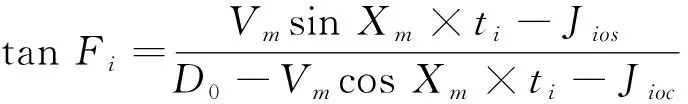
(3)
可由该式求解目标的航速、舷角等运动参数。
对于本舰的运动参数在这里不作讨论,但是本舰必须进行至少一次的适当机动,才能确保目标运动参数解的唯一性。
2 理论基础
2.1 纯方位目标运动的匹配场处理方法
匹配场处理技术的基本原理:依据已知的海洋环境噪声及声传播信道特性,利用数学模型计算得到拷贝场,将其与水听器阵实际接收到的声信号进行匹配处理,根据目标函数的大小判断匹配度,确定实际声源的具体信息,最后实现定位水下声源的目的。匹配场处理技术自提出以来,在水下声源定位以及海洋参数反演发挥着重要作用。
纯方位目标运动分析的匹配场方法是指在已知接收阵信息时,根据匹配场处理技术,建立模型,形成理论预测的目标方位场,也称拷贝场,将其与实际测量方位场进行谱估计处理,寻找最优匹配结果,与这一结果对应的目标运动要素就是希望得到的结果。这一处理过程如图2所示。其中F(n)copy为方位拷贝场,F(n)obs为方位实测场。
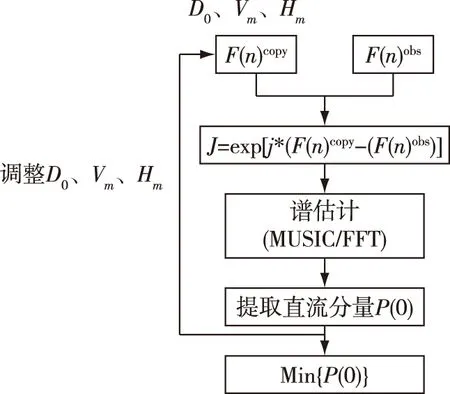
图2 匹配场处理流程
本文在目标函数的选取上,将ΔF(n)=F(n)copy-F(n)obs引入相位中,即将数值匹配转变为提取直流交流信号的问题,为谱估计方法提供了可能。
2.2 子空间MUSIC算法
MUSIC算法是基于子空间分解而产生的一种方法。根据子空间理论,N维样本空间可以分解为信号子空间和噪声子空间,令信号子空间的维数为M维,则噪声子空间的维数为N-M维。将子空间MUSIC算法用于纯方位目标运动分析中,将ΔF(n)引入相位中,即J=exp[j*(F(n)copy-F(n)obs)],使之成为目标函数,则将方位匹配问题转变为提取直流交流信号的问题。利用子空间MUSIC算法可提取直流成分,即最优匹配ΔF(n)=0。遍历搜索所有目标运动参数(即目标初始距离D0,目标航速Vm,目标初始航向Hm)取值区间的数值,由于最优匹配时,直流成分的信号最弱,即MUSIC算法提取出的直流成分的值最小,为找到最优匹配的值,则需要在所有直流成分中找到最小值,对应的目标参数取值区间中的距离D′0、航向H′m、航速V′m,即为希望得到的最优匹配值。
2.3 快速傅里叶变换原理
快速傅里叶变换是离散傅氏变换的快速算法,它是根据离散傅氏变换的奇、偶、虚、实等特性,对离散傅里叶变换的算法进行改进获得的[10]。
通过快速傅里叶变换,对目标函数进行频谱分析,提取其中频率为0时的能量即直流分量,同样比较直流分量大小,当直流分量最小时,对应的参数取值即为最优匹配值。
3 仿真实验与结果分析
在本文所做的仿真实验中,令初始时刻t0=0,初始时刻时,目标初始方位为0°,初始距离为D0=10 km,目标与观测平台在同一平面内运动,且目标保持等速直航(即目标的航速和航向保持不变),航速Vm为5 m/s,将目标航向Hm分别设置为135°和150°,观测平台的速度保持匀速3 m/s。初始时刻,观测平台的运动方向与y轴正方向夹角为30°,两分钟后,观测平台进行一次机动,速度保持不变,角度顺时针转向30°(即与y轴正方向夹角为60°),再进行等速直航。仿真实验中,采样率fs=2 Hz。
3.1 子空间MUSIC算法的仿真与结果分析
实验参数设计:目标与观测平台的初始距离搜索范围是6 km~14 km,步长为400 m;目标初始航向的搜索范围90°~180°,步长为5°;航速的搜索范围为1~10 m/s,步长为2 m/s。需要注意:由于观测平台在t=2 min时进行了一次机动,所以在没有进行机动之前(t<2 min时),该模型无解,因此,本文对t>3 min的仿真结果进行分析。
实验1:目标初始航向Hm=135°,噪声标准差std1=0.1;
实验2:目标初始航向Hm=150°,噪声标准差std1=0.1;
实验3:目标初始航向Hm=135°,噪声标准差std2=0.3;
实验4:目标初始航向Hm=150°,噪声标准差std2=0.3。
由图3~6可知,子空间MUSIC算法对航速不敏感,误差较大。对初始航向和初始距离的估计相对较好。从收敛性来看,子空间MUSIC算法收敛性较差,其结果不平稳,且具有较大起伏,不能准确而稳定地收敛到真值。可以得出:1)噪声干扰对子空间MUSIC算法结果具有一定影响;2)利用子空间MUSIC算法进行纯方位TMA处理时,针对不同目标初始航向,该算法对不同运动参数的敏感度不同,会出现相对误差过大的情况。

图3 实验1仿真结果(距离、航向、航速)

图4 实验2仿真结果(距离、航向、航速)
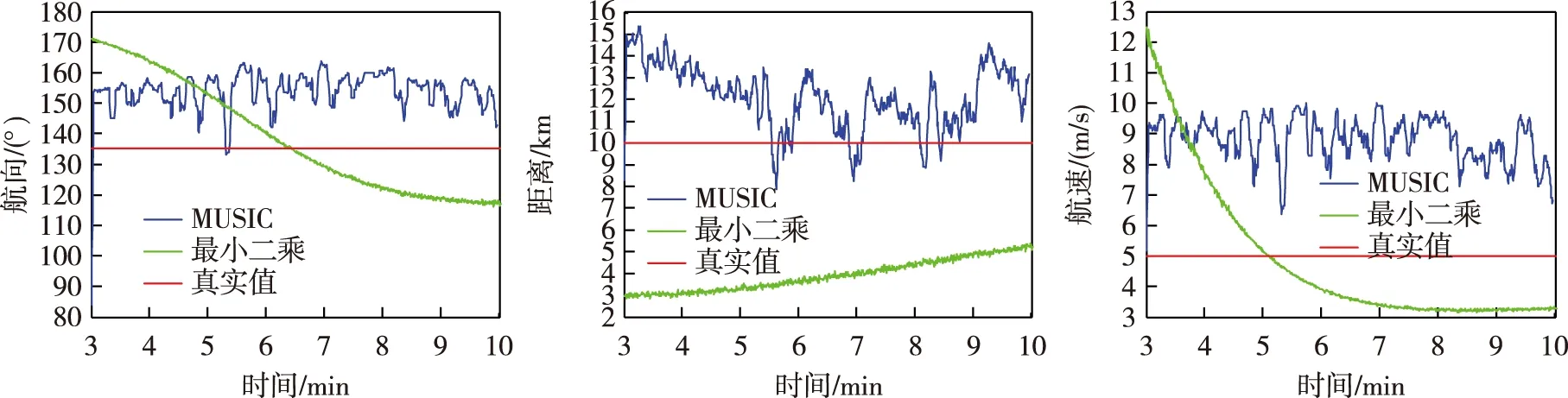
图5 实验3仿真结果(距离、航向、航速)

图6 实验4仿真结果(距离、航向、航速)
经分析,子空间MUSIC算法收敛性较差的问题与目标函数选取有关。图7表示所选取目标函数与目标参数空间中距离的关系。
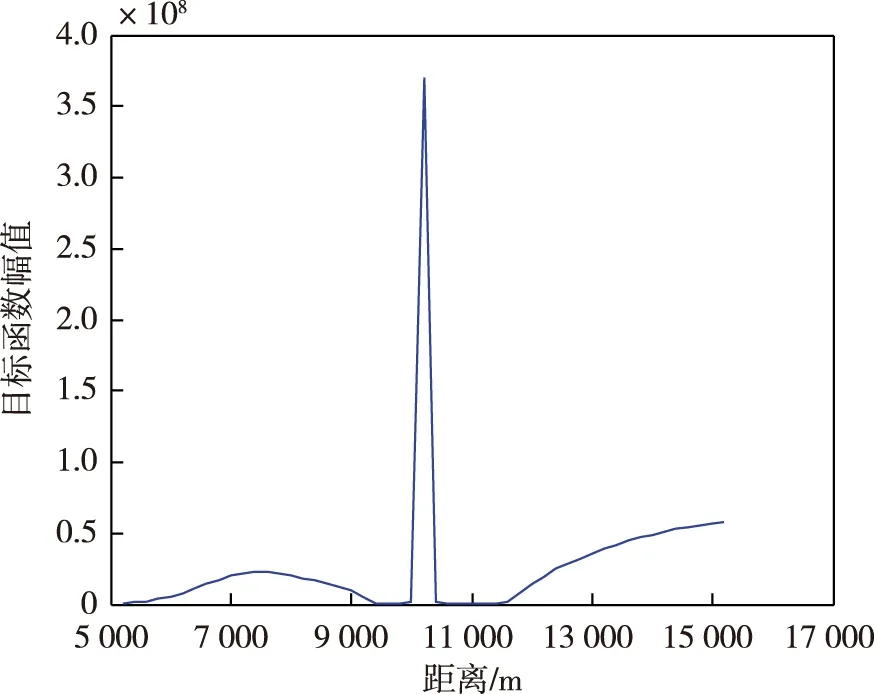
图7 目标函数与参数空间中距离的关系
从图中可以明显看出,当距离取到真值时,目标函数的幅值显著升高,形成一个非常尖锐的峰,这说明在利用子空间MUSIC算法估计目标运动要素时,需分辨率较高。由于背景噪声的干扰,实际真实值的位置会偏离理论值很小的范围。但由于计算机存储空间的限制,实际仿真实验中选取步长相对过大,不能准确搜索到极大值点,导致实际运算结果与真值差异较大且起伏明显。当计算机运算量满足要求时,子空间MUSIC算法有望获得较小的相对误差,从而得到较为准确的估计结果。
3.2 运用傅里叶变换进行谱估计的仿真与结果分析
针对3.1中提出的大步长误差过大且不稳定的问题,可以假设:在大步长的情况下,若目标函数的大小受运动参数取值变化的影响不显著,理论上应该获得更高精度的估计结果。由于傅里叶变换分辨率较低,目标函数随运动参数(图8中运动参数为距离)变化较缓,在真值附近很大范围内,目标函数都保持较大的幅值,因此,在大步长时,运用快速傅里叶变换进行谱估计处理更容易获得与真值更为接近的结果。为方便比较,设置同样参数的4组实验。
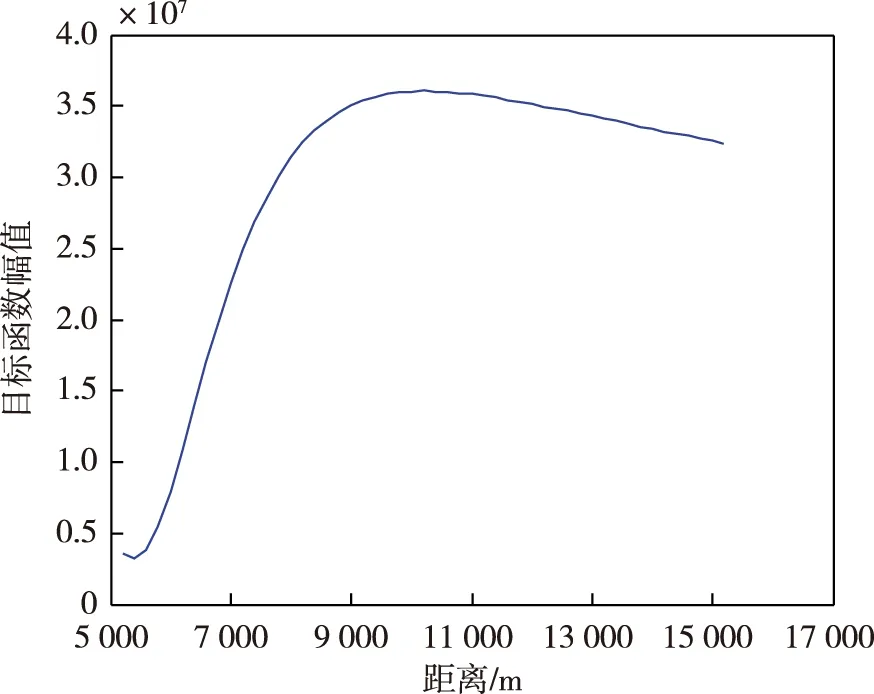
图8 目标函数与参数空间中距离的关系
实验5:目标初始航向Hm=135°,噪声标准差std1=0.1;
实验6:目标初始航向Hm=150°,噪声标准差std1=0.1;
实验7:目标初始航向Hm=135°,噪声标准差std2=0.3;
实验8:目标初始航向Hm=150°,噪声标准差std2=0.3。
由此可以得出结论,运用快速傅里叶变换方法进行纯方位TMA处理时,由于目标函数幅值随目标运动参数的变化缓慢,利用快速傅里叶变换方法对目标运动参数进行解算时,得到的结果更加稳定,收敛效果更加明显。在给定步长较大的情况下,利用快速傅里叶变换方法进行谱估计能得到更为准确的结果。
由图9和图10中可以看出,在小背景噪声(std1=0.1)时,快速傅里叶变换方法能够在很短的时间(4~5 min)内收敛到真值附近很小的范围,解算精度较高且收敛时间较短,在背景噪声较大(std1=0.3)时(图11和图12),快速傅里叶变换方法也能在6~7 min左右收敛,解算精度也较高。但目标函数变化较缓也存在其相应的缺点,正由于目标函数随运动参数变化较缓,使得目标函数在真值附近较大区域都有较大的幅值,使得匹配场处理结果不能准确找到真值,而是在真值附近存在一定的相对误差。
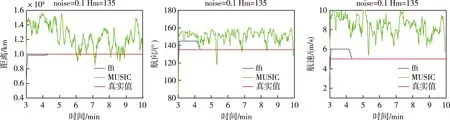
图9 实验5仿真结果(距离、航向、航速)
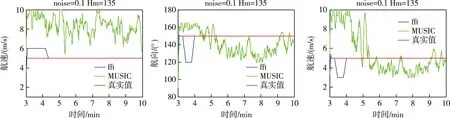
图10 实验6仿真结果(距离、航向、航速)
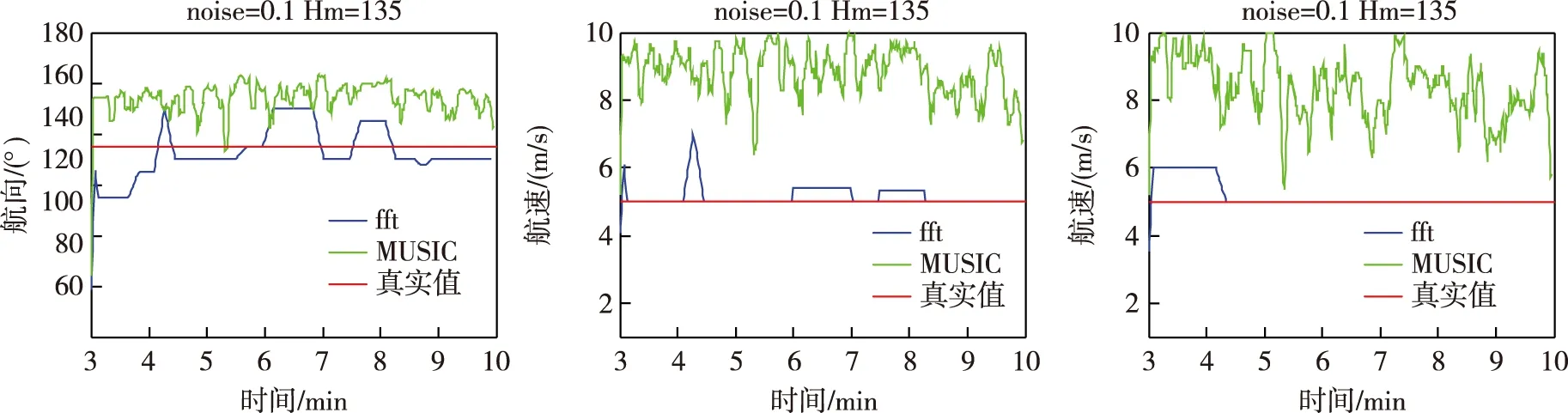
图11 实验7仿真结果(距离、航向、航速)
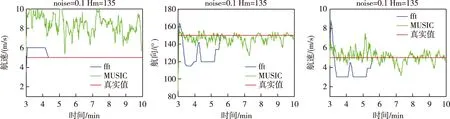
图12 实验8仿真结果(距离、航向、航速)
4 结束语
本文利用水声匹配场的思想建立了BTMA的匹配处理模型,将BTMA改建为谱估计问题,进一步引入信号处理领域的MUSIC谱估计和快速傅里叶变换形成功率谱估计目标运动参数。仿真结果表明:1)由于计算机存储空间的限制,子空间MUSIC算法仿真实验中的搜索步长较大,仿真结果在真值附近波动较大,不能准确而稳定地收敛到真值。因此,MUSIC算法在对纯方位TMA进行处理时稳定性不高,不建议使用。2)快速傅里叶变换方法在处理纯方位TMA时稳定性较高,精度也较高。当匹配值在真值附近较大范围时,目标函数的幅值都较大,且随运动参数的变化不明显。所以在采用大步长的情况下,快速傅里叶变换方法在进行纯方位目标运动分析时能得到更准确的结果。
