以试题命制撬动教材研究的实践与思考

刘雪明

【摘 要】高中数学教材是实现数学课程目标、发展学生数学学科核心素养的重要教学资源。然而受升学、考试等因素的影响，很多教师不太重视教材的研究，只把教材简单当做习题集来使用。为改变这一现象，在命制区域统考试题时，应有意从教材中选取素材、设计试题，以激发教师研究教材、使用教材的热情，充分发挥教材的价值。

【关键词】教学资源;教材研究;命制试题

【中图分类号】G633.6  【文献标识码】A  【文章编号】1671-8437（2021）10-0150-02

高中数学教材为“教”与“学”活动提供了学习主题、基本线索和具体内容，是实现数学课程目标、发展学生数学学科核心素养的重要教学资源。为了落实课程改革精神，促进教师的“教”和学生的“学”，教材编者在素材选取、栏目设计、活动方式、情境类型、思路引领、习题选择、图文表达形式等方面都进行了精心设计。然而，受升学、考试以及名校效应等因素的影响，很多教师过分采用名校的教辅资料，不太重视教材的研究，只把教材简单地当做习题集来使用，将课堂教学变成解题教学，甚至变成题型教学。为了使数学教学回归本质，实现数学学科的育人目标，激发教师和学生研究教材、使用教材的热情，充分发挥教材的价值，在命制区域统考试题时，应有意从教材中选取素材、设计试题，注重试题的基础性、综合性、应用性、创新性，力图通过区域评价来引导一线教师进行教材研究、课堂教学改进。

1   利用教材素材命制试题的实践

素材1：摩天轮是生活中常见的娱乐设施，许多学生都有坐摩天轮的经历。摩天轮还是反映周期运动的重要模型，是学习三角函数的很好素材。高中数学教材必修4的第一章基本初等函数（二）（即三角函数）、第三章三角恒等变换都以摩天轮为背景引出相应章节的学习内容。在学习角的概念、三角函数线、正弦型函数等知识时，又多次提到摩天轮。为激发学生的兴趣，让学生感到数学就在身边，数学是有用的、好玩的，可以摩天轮为背景命制试题[1]。

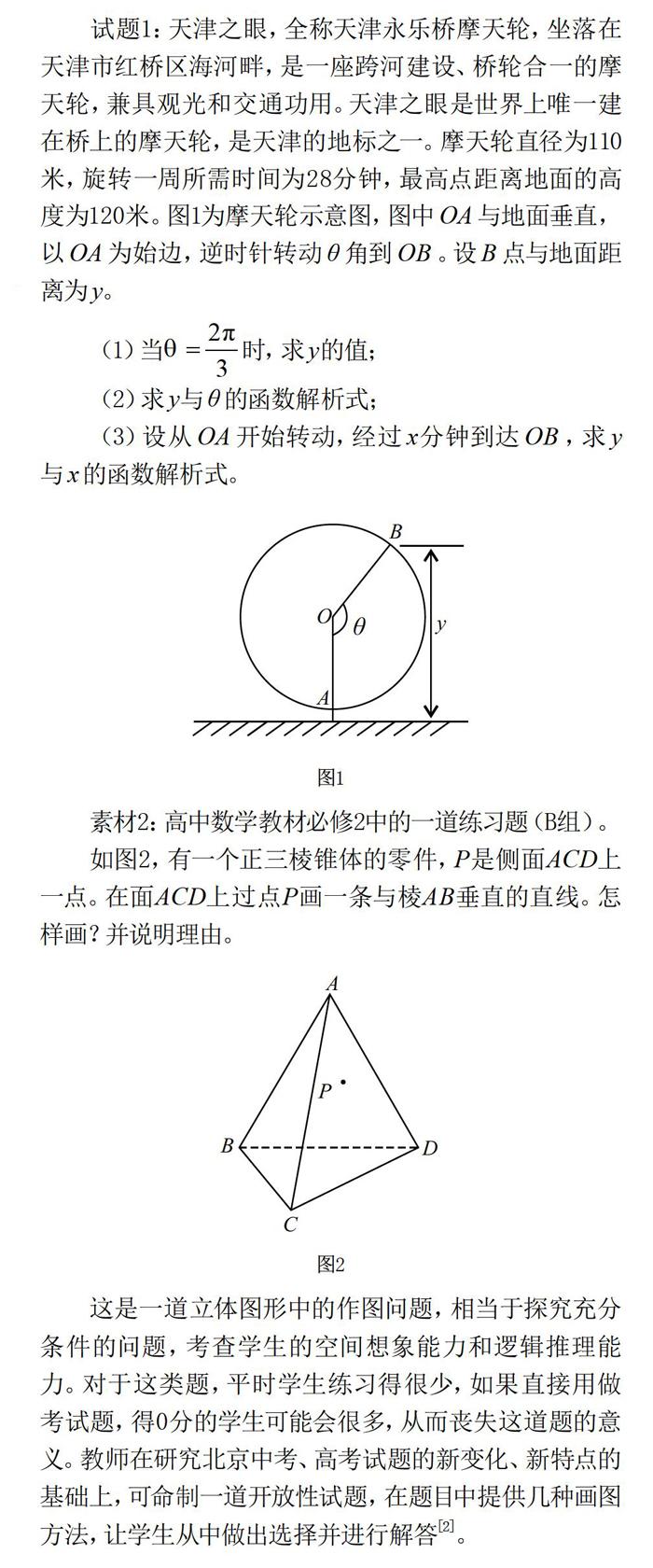
试题1：天津之眼，全称天津永乐桥摩天轮，坐落在天津市红桥区海河畔，是一座跨河建设、桥轮合一的摩天轮，兼具观光和交通功用。天津之眼是世界上唯一建在桥上的摩天轮，是天津的地标之一。摩天轮直径为110米，旋转一周所需时间为28分钟，最高点距离地面的高度为120米。图1为摩天轮示意图，图中 OA 与地面垂直，以 OA 为始边，逆时针转动 θ 角到 OB 。设 B 点与地面距离为 y。

（1）当时，求 y的值;

（2）求 y与 θ 的函数解析式;

（3）设从 OA 开始转动，经过 x分钟到达 OB ，求 y与 x 的函数解析式。

素材2：高中数学教材必修2中的一道练习题（B组）。

如图2，有一个正三棱锥体的零件，P是侧面ACD上一点。在面ACD上过点P画一条与棱AB垂直的直线。怎样画？并说明理由。

这是一道立体图形中的作图问题，相当于探究充分条件的问题，考查学生的空间想象能力和逻辑推理能力。对于这类题，平时学生练习得很少，如果直接用做考试题，得0分的学生可能会很多，从而丧失这道题的意义。教师在研究北京中考、高考试题的新变化、新特点的基础上，可命制一道开放性试题，在题目中提供几种画图方法，让学生从中做出选择并进行解答[2]。

试题2：如图2，有一个正三棱锥体的零件，P 是侧面ACD 上一点，欲在面 ACD 上过点 P 画一条与棱 AB 垂直的直线，怎么画？

为解决上述问题，甲、乙、丙三位学生给出了如下3种画法：

学生甲：过点 P 做 CD 的平行线 l ，则 l 与 AB 垂直。

学生乙：过点 P 做 CD 的垂线 l ，则 l 与 AB 垂直。

学生丙：连接 PC ，则 PC 与 AB 垂直。

从三位学生的回答中任意选择一个，判断该学生的画法是否正确，并说明理由。

分析：学生做出选择和判断后，问题就变成了结构良好的试题。如果选择甲，结论是肯定的，试题转化为学生熟悉的形式;如果选择乙、丙，结论是否定的，一般采用反证法进行证明（教材中有简单介绍）。在用反证法进行证明时发现“正三棱锥”不够严格（以 A 为顶点的三个角不能是直角），应该改为“正四面体”。

素材3：高中数学教材2-2中有段文字：如果在f'（x）=0 的根 x=x0 的左、右两侧， f'（x） 的符号不变，则f（x0） 不是极值。如对于函数f（x）=x3 有 f'（0）=0，但 x=0 不是极值点。这就是说， f'（x）=0的根不一定都是函数的极值点。由此可见，可导函数f（x）在点 x0 取得极值的充分必要条件是f'（x0）=0，且在 x0 左侧与右侧， f'（x） 的符号不同。很明显， f'（x0）=0是 x0 为极值点的必要条件，并非充分条件。

此段文字的目的，是以具体函数f（x）=x3 为例，说明f'（x0）=0与 x0 为极值点之间的关系，从而强调求函数极值的一般步骤中，判断 x0 左侧与右侧f'（x） 的符号异同的必要性。其实， f（x）=x3是个很重要的函数，可以说明f'（x）≥0 与f（x） 单调递增之间的关系，还可以加深对切线定义的全面理解[3]。

试题3：已知函数f（x）=x3+1 ，关于这个函数给出以下三个命题：

（1）函数f（x） 在定义域上是增函数;

（2）x=0是函数f（x） 的极值点;

（3）y=1是曲线 y=f（x） 的一条切线;

其中真命题的序号是_______。

2   思考与展望

作为命题者，为了在教材中发现有价值的素材，要全面通读、深入研究教材;为了保证试題的科学性，要对教材进行理性思考、科学论证;为了使试题符合学生的认知水平，要研究学生解决问题的思维过程与特征;为了保证试题有新意、有时代性，要研究高考的新政策、新变化，注意学科间的渗透和交叉，拓宽试题的情境。经过一段时间的实践，不仅可以积累大量优秀题目，命题者对各方面的素材也能保持高度的敏感性，专业素养得到提高。作为一线教师和学生，为了正确解答试题，取得理想成绩，要研究命题者的出题意图、考查内容、素材来源，提高对教材的重视程度和研究教材的自觉性。经过一段时间的实践，无论是命题者还是一线教师对教材的价值都会有更全面的认识，研究教材的自觉性也会增强，同时积累丰富的阅读教材、理解教材、使用教材的经验[4]。

《普通高中数学课程标准》（2017版）在基本理念、课程目标、课程结构、课程评价等方面都有比较大的变化，特别是凝练出了学科核心素养和学业质量标准。课程标准在命题建议中指出“要充分考虑命题对教学的积极引导作用”，“考查内容应围绕数学内容主线，聚焦学生对重要数学概念、定理、方法、思想的理解和应用，强调基础性、综合性;注重数学本质、通性通法，融入数学文化”，“应有一定数量的应用问题、开放性问题、探究性问题”。相应的，新版教材也有非常大的调整，研究教材、理解教材、使用教材是理解和落实新课程理念的重要抓手和有效途径，同时新教材也为课堂教学、考试评价提供了更新的素材，教材研究、试题命制永远在路上。

【参考文献】

[1]中华人民共和国教育部.普通高中数学课程标准（2017版）[M].北京：人民教育出版社，2018.

[2]普通高中课程标准实验教科书人教B版数学必修2[M].北京：人民教育出版社，2013.

[3]普通高中课程标准实验教科书人教B版数学必修4[M].北京：人民教育出版社，2013.

[4]普通高中课程标准实验教科书人教B版数学选修2-2[M].北京：人民教育出版社，2013.