基于离散傅里叶变换的直流微电网储能调控方法研究

李 明，刘国营，张国锋，张海玉，李小沛

（1.国网新疆电力有限公司电力科学研究院，新疆乌鲁木齐 830011；2.国网新疆电力有限公司吐鲁番供电公司，新疆 吐鲁番 838000）

储能结构是微电网中不可或缺的一部分，在微电网中承担电流沟通、平滑电荷、备用负荷的作用，能够减缓微电网在电力传输中的压力[1]。随着微电网构建规模的不断扩大，对于微电网的储能调控需求不断增强，为此，需不断调整直流微电网的电流流通方式，实现对其的调控操作[2]。

在文献[3]中，利用离散傅里叶变换对可再生能源的输出功率进行频谱分析，以优化能量储存分配，平滑其功率波动。对于独立微电网，考虑到储能设备的循环寿命，文献[4]通过分析微电网的负荷谱来优化混合储能配置。为提高有功配电网络的灵活性。文献[5]建立了一个同时考虑了电力需求边际和弹性需求边际机会约束的能量储存能力优化模型。

文中引入离散傅里叶变换方法分析微网产生的负荷功率，进而确定联络线功率，分析电池和超级电容功率，在判断不同功率的分配方式后，给出了最佳的调控方案。

1 直流微电网储能数据获取

离散傅里叶能够将时域信号转换到频域信号中，同时根据自身的数据调控性能调整不同的信息，加强内部转化能力，在获取数据后，将数据分离，并构建完整的数据流转通道，完成对数据的调整操作[6-8]。为此，文中利用离散傅里叶技术将直流微电网储能数据收集至中心区域中，并配合数据检测操作，结合处理后的电网运行异常值数据实施检测操作。采用离散傅里叶内部的转化功能提取主导信息的数据，集中加大对中心数据的管理力度，将离散傅里叶变换性能完美融合到检测手段中。构建电网数据网络拓扑结构，并设置一个完整子集，为主体空间提供一定的能源供应，将整合的数据收录至中性空间中，时刻准备进行数据数值检测[9-12]。建立的电网数据拓扑结构如图1 所示。

图1 电网数据拓扑结构

控制变换算法的运算数据量，避免因操作进度过激造成的数据丢失状况。构建变换算法公式如下：

式（1）中，P表示变换算法参数，u表示内部数值检测参数，v表示电网数据能源参数[13]。

研究分布式存储模式，不断整理存储空间，增加信息检测内容，促使检测结果的精准性更高，不断追踪检测结果数据。采用主从结构管理研究数据并进行节点数据访问操作，将访问的信息定时报告给区域电网系统中，时刻查找此时的数据存储状态，并利用不同阶段的数据信息构建中心数据处理空间系统。在构建的处理空间中开拓新兴的数据获取通道，并固定通道的流通方向，将所有的数据收集至该通道中。同时存储通道数据，将属于同一种类的数据集中分配至相同的集合中等待数据处理操作[14]。

管理此刻的直流微电网数据内容，并将该数据内容存储在数据获取中心中，实现对于直流微电网数据的获取操作[15]。

2 基于离散傅里叶变换的直流微电网储能数据处理

在实现数据获取后，利用离散傅里叶变换法实现电网储能数据处理。利用傅里叶变换，可以将时域信号转换成频域信号，通过分离、滤波和截取实现对信号的分解[16]。对日常微网负荷选取的样本数据进行采样分析，采样频率为f，采样点数为t。采用离散傅里叶变换进行净负荷功率微型智能电网数据处理过程中，采样结果与振幅、频率计算公式如下：

根据离散傅里叶变换公式的对称性，分析幅频特性，根据式（2）可知，分解频率取值为fs/T、2fs/T、3fs/T。为了能够使取值更加方便，设定分界点为a，根据分界点数值处理离散傅里叶变换的直流微电网储能数据。

采用联络线功率对直流分量和低频负荷波动进行补偿，其余由电池和超级电容补偿。在此基础上，根据补偿频率范围的划分，将幅值补偿频带外设为零，相应的幅值补偿频带保持不变，并在时域上进行傅里叶反变换，得到超级电容的补偿功率分配公式，如下：

其中，P0表示直流微电网分配处理得到的补偿功率，S0表示补偿功率的补偿范围。

3 直流微电网储能调控

根据得到的补偿功率数值进行直流微电网储能数据调控，分别设立分界点n1、n2。调控过程如图2所示。

图2 直流微电网储能调控

由图2 可知，分界点nl、n2 对于联络线的功率以及直流微电网储能调控的功率分配有着决定性的作用，这也代表着分界点直接影响着联络线的利用率。因此文中采用穷举法确定分界点，使分界点的选择得以优化。

分界点n1 负责判定联络线电源的分布方式，在确定分界点n1 后也可以很好地分析混合储能系统的分布方式，如果分界点n1 选择出现某种错误，就会产生某种功率波动。对并网微网而言，功率波动过大将影响到微网的并网效果，因此分界点n1 值的选择应满足联络线功率波动的要求。对于n1 值满足的能量波动需求结线，采用穷举法比较每条结线在n1 值上的利用率，以选择最大的分界点结线作为最终结果。

微电网通过联络线与大电网相连，联络线路承担了微网络和大网络的双向交互作用，这种技术不但可以向微网并网，也可以向大电网传输多余的电能。联络线路利用率，是指某一时期联络线路的实际发电量与其最大传输容量的比率，联络线路的利用率在一定程度上反映了配电网络资产的利用率。

电网的利用率计算公式如公式（4）所示。

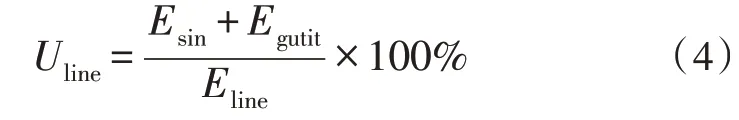
其中，Uline代表联络线利用率，Esin表示调度过程中大电网向微电网传输的电量，Egutit表示调度过程中微电网向大电网传输的电量，Eline表示额定功率下输送的电量。

分界点n2 对于电池和电容的分配功率会产生一定的影响，当分界点过多时，电池的充放电次数也会随之增加，电池的使用寿命会因此而降低，这对于微电网储能系统是十分不利的，而如果分界点过小，则电容配置效果很差，电容混合能源系统的价格也会随之增加，因此需要运用穷举法求解不同n2 值人群混合储能能力的优化模型，确定在不同边界点条件下的混合储能成本，并以成本最低的边界点及其相应的混合储能结构为优化结果。

4 实验与研究

为验证基于离散傅里叶变换的直流微电网储能调控方法的调控效果，进行对比实验。

设定分界点分别为52、51，选取传统的基于遗传算法的直流微电网储能调控方法和基于小波计算法直流微电网储能调控方法以及文中研究的基于离散傅里叶变换的直流微电网储能调控方法对同一直流微电网进行储能调控。直流微电网结构如图3所示。

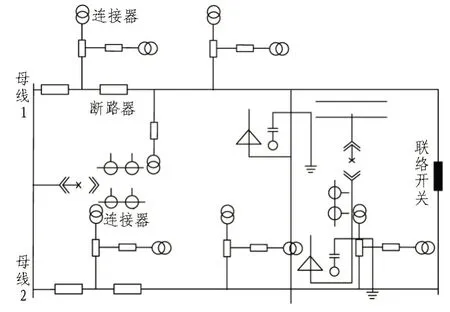
图3 直流微电网结构

设定实验参数如表1 所示。根据表1 参数进行实验，得到的实验结果如图4 所示。

表1 实验参数

根据图4 可知，文中研究的方法调控负荷功率远小于传统方法功率。文中方法对微网调整方法进行了研究，利用离散傅里叶变换对微网净负荷功率谱进行了分析，建立了两级混合储能优化模型，并分别对联络线进行了改进。最佳化的目的是提高混合能量的利用率，降低其储存成本。通过对联络线功率和混合储能边界点的求解，在满足接线功率波动要求的基础上优化了接线功率。对蓄电池和超级电容的截断点进行了优化，找到了混合储能容量的最佳配置方案，从而降低了储能成本。文中的研究方法通过离散傅里叶变换方法对数据进行逆变换，通过优化的方式得到分界点，改变电网的负荷功率，从而得到联络线，有效确保混合储能容量配置。离散傅里叶变换方法能够更好地分析调度模型，从而解决直流微电网内部的储能优化配置问题，在实际问题中，也可以根据具体实际状况，降低计算量。

图4 调控负荷功率对比

5 结束语

文中在传统直流微电网储能调控方法研究的基础上，提出了一种新式基于离散傅里叶变换的直流微电网储能调控方法，转化了不同的电网电流调控方式，同时配置了相关性较强的内部数据信息，更好地提升了数据操作能力，具有较高的调控性能。实验研究表明，文中直流微电网储能调控方法研究的调控效果明显优于传统直流微电网储能调控方法研究的调控效果。