红层滑坡滑带土蠕变力学特性及经验模型研究
2021-06-11魏良帅黄海峰
贾 逸,魏良帅,黄海峰
(1.中国地质科学院探矿工艺研究所,四川 成都 611734;2.中国地质调查局地质灾害防治技术中心,四川 成都 611734;3.四川成绵苍巴高速公路有限责任公司成都分公司,四川 成都 641400)
0 引 言
红层在我国西南地区广泛分布,孕育了大量滑坡体,威胁人类生命财产安全[1-2]。滑带是指在滑坡发育、发生过程中经历物理化学作用,力学性质大幅衰减的下滑界面[3]。当滑带土蠕变累积至某一程度,易在降雨、地震等外界因素的诱发下发生滑坡。因此,研究滑带土蠕变力学特性对边坡长期稳定性分析及灾害防治具有十分重要的意义[4]。对于滑带土蠕变的研究已有较多成果,赖小玲等[5]在传统Mesri蠕变经验模型的基础上,将基质吸力作为独立变量,建立考虑基质吸力的滑带土蠕变经验模型;Bhat等[6]采用扭剪蠕变仪研究滑带土在残余状态下的蠕变行为;Maio等[7]开展直剪蠕变试验,研究孔隙水含盐量对滑带土残余蠕变强度的影响;Wen等[8]研究发现含砾量与滑带土蠕变强度之间无直接关联;李梦姿[9]构建了滑带土非线性Burgers模型;黄海峰等[10]通过Log-Modified函数描述应变-时间关系,建立新的滑带土蠕变经验模型;蒋树等[11]引入非线性黏塑性损伤元件,改进传统Cvisc模型,对滑带土蠕变行为模拟取得良好成效;朱荣森[12]以黄土滑坡滑带土为研究对象,开展三轴压缩蠕变试验,得到蠕变力学性质与含水率和围压之间的规律。
土体蠕变本构模型以针对性较强的经验模型和适用性较强的元件模型为主。经验模型由于拟合参数无明确物理意义难以推广。为解决经验模型适用性弱的难题,本文在传统Mesri经验模型的基础上,保留原有双曲线方程描述应力-应变关系,引入分数阶微积分理论反映土体应变-时间关系,使经验模型参数物理意义更为明确,得到改进后的蠕变经验模型。利用该模型对西南地区某红层滑坡滑带土和相关文献中的黄土和高含盐细砂土蠕变数据进行辨识对比,证明本模型的可行性和适用性,可为土体蠕变经验模型构建及红层边坡长期稳定性分析提供参考。
1 滑带土蠕变试验
1.1 试样制备及试验仪器
试样取自西南地区某红层滑坡滑带,由于钻孔取样时不可避免有一定扰动,取原状土条件受限,故本文以重塑样进行固结不排水三轴压缩蠕变试验。土样密封运回试验室风干后将其碾散,过1 mm筛,通过击实法并以天然含水率12%制备直径39.1 mm、高度80 mm的圆柱体试样,最大允许差值在1%以内,符合GB/T 50123—2019《土工试验方法标准》的规定,用保鲜膜充分包裹,静置1 d使试样水分均匀。土样物理力学参数见表1。

表1 土样物理力学参数
试验仪器为CSS-2901TS土体三轴流变试验机。该试验机由轴向加载系统、围压加载系统和变形测量系统等组成,最大轴向荷载达10 kN,围压及孔隙水压力变化范围皆为0~2 MPa,轴向位移量测范围为0~20 mm。
1.2 试验方法
首先开展滑带土三轴不排水剪切试验,得到不排水剪切强度τf。由于滑带在滑坡体内所处位置较浅,实际围压较低,故将围压设置为100、200 kPa和300 kPa,应力水平D取为0.5、0.55、0.6、0.65、0.7和0.75,则每级偏应力对应为0.5τf、0.55τf、0.6τf、0.65τf、0.7τf和0.75τf。应力路径示意见图1(以围压100 kPa为例)。蠕变试验加载方案见表2。蠕变试验首先以0.2 kPa/min的速率将围压加载至预定值,接着固结土样,固结时间设定为4 h,之后再以0.05 mm/min的剪切速率施加剪切荷载,每0.2 mm的剪切位移记数1次。

表2 蠕变试验加载方案 kPa

图1 应力路径
2 试验成果
2.1 滑带土蠕变曲线
通过图1所示应力路径开展固结不排水三轴蠕变试验,得到分级加载蠕变曲线,见图2;通过Boltzmann线性叠加[13]处理图2,绘制分别加载蠕变曲线,见图3。图2、3中,将各级应力水平标识于曲线上。从图2可看出,分级加载蠕变曲线为“台阶式”攀爬的曲线,每一级“台阶”高于前一级。高围压下的应变量值总是大于低围压。从图3可看出,土样在加载瞬间首先表现出瞬弹性变形,紧接着是历时较短的衰减蠕变阶段,该阶段曲线斜率逐渐降低,蠕变速率递减,随后进入稳定蠕变阶段,此时蠕变速率基本保持平衡,应变量值基本保持恒定。土样轴向应变由瞬时应变和蠕变应变组成,蠕变应变包含衰减、稳定蠕变阶段。围压300 kPa时,第6级加载下稳定蠕变阶段的曲线斜率呈明显增大趋势,说明蠕变变形现象更为显著。对于同一滑带土,随着土体垂直压力的增加,围压不断增大,轴向应变值递增。

图2 分级加载蠕变

图3 分别加载蠕变
2.2 滑带土的等时偏应力-应变特性
从图3中择取1、11、21、31、41、51、61 h和71 h共8个时间节点的偏应力和应变值,绘制等时偏应力-应变曲线,见图4。从图4可以看出,滑带土等时偏应力-应变曲线近乎为一束曲线簇,其形态近似为双曲线,具有明显的非线性特征。蠕变时间为1 h的曲线与11、21、31、41、51、61 h和71 h这7条曲线组成的曲线簇明显分离,这说明土样在初始荷载下存在明显的弹性变形,第1级加载情况下尤为显著。分析可知,滑带土总应变由瞬时弹性应变和蠕变应变组成。

图4 等时偏应力-应变关系
3 蠕变经验模型
3.1 经验型蠕变模型的建立
滑带土总应变由瞬时应变和蠕变应变组成,暂不考虑瞬时应变,将滑带土蠕变应变ε2表示为
ε2=f1(k)f2(t)
(1)
式中,f1(k)、f2(t)分别为土样的应力-应变关系函数、应变-时间关系函数;k、t分别为函数f1(k)、f2(t)的自变量。
3.2 应力-应变关系
由于滑带土等时偏应力-应变曲线近似双曲线,参考传统Mesri经验模型[14]引入Kondner双曲线型偏应力-应变方程,即
(2)
式中,σ1、σ3分别为最大和最小主应力;a、b为双曲线方程参数。
对式(2)等号两侧同时求微分,得到初始切线模量Eu为
(3)
当ε→∞时,对式(2)取极限值即为最终偏应力差(σ1-σ3)ult,即
(4)
实际上,土样应变不可能无穷大,当外界荷载达到排水剪切强度τf时土样开始破坏。为了在Kondner双曲线中体现破坏点[εf,(σ1-σ3)f],其中,εf为破坏点对应的应变,(σ1-σ3)f为破坏偏应力。引入破坏比Rf[5],公式为
(5)
将式(3)、(5)代入式(2)得到应力-应变本构关系式,即
(6)
式中,D=(σ1-σ3)/(σ1-σ3)f。
3.3 应变-时间关系
蠕变经验模型中,应变-时间关系多通过双曲线函数、幂次函数和对数函数甚至生长函数等[10,15]多种形式进行描述,尽管能取得一定的拟合效果,但会导致应力-应变关系参数无实际物理意义,难以表征蠕变发展过程的内在性质,且由于其具有较强的针对性,无法进行推广,故本文引入分数微积分理论反映土样应变-时间关系。
分数阶微积分的核心在于其阶数为有理分数、无理数和复数,可表征与某一现象的整个发展历史有关的性质[16]。分数阶微积分物理意义清晰,结构简单,在非线性动力系统中优势显著。滑带土是一种非线性的地质材料,故引入应用较为广泛的Riemann-Liouville型分数阶微积分。依据该理论,函数f(t)在可积区间[0,t]的α阶Riemann-Liouville积分定义为
(7)
式中,Γ(α)为伽马函数,α为大于0的分数阶数;s为用于拉普拉斯变换的某一自变量。 函数f(t)的α阶微分相应地定义为
(8)
式中,n=[α]。Γ(α)定义为
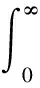
(9)
在滑带土蠕变发展过程中,土样蠕变应变一般用牛顿体本构方程描述,即
(10)

基于分数阶微积分理论,可将该本构关系其转化为
(11)
式中,ηα为分数阶黏滞系数。
当应力σ恒定时,依据Riemann-Liouville积分理论,对式(7)进行Riemann-Liouville分数阶积分得
(12)
式(12)即为土样应变-时间关系。取σ为200 kPa,ηα为5×105kPa·h,通过式(12)绘制不同α值的蠕变曲线,见图5。从图5可看出,当α增大时,曲线斜率不断增加,曲线逐渐远离时间轴,表现出明显的非线性特征;当α增至1时,表现出完全线性关系。

图5 不同α值的蠕变
3.4 经验型蠕变模型
将式(6)、(12)同时代入式(1)可得
(13)
瞬时弹性应变ε1服从Hooke定律,ε1=σ/Eu,由于式(13)未考虑瞬时应变,故将式(13)改为
(14)
由于D=(σ1-σ3)/(σ1-σ3)f,将其代入式(14)化简可得
(15)
式(15)即为本文所建蠕变经验模型。
4 模型验证及参数求解
传统经验模型皆是分别求解应力-应变关系和应变-时间关系参数,实际土体蠕变发展过程中变形同时受到应力和时间的影响,通过应力-应变-时间模型整体同时求解参数更为合理。本文建立的蠕变经验模型有Eu、Rf、ηα和α共4个参数,通过一般的非线性最小二乘算法求解即可。模型参数见表3。引用文献[14]中传统Mesri经验模型与所建模型进行对比,理论值与试验值对比曲线见图6。
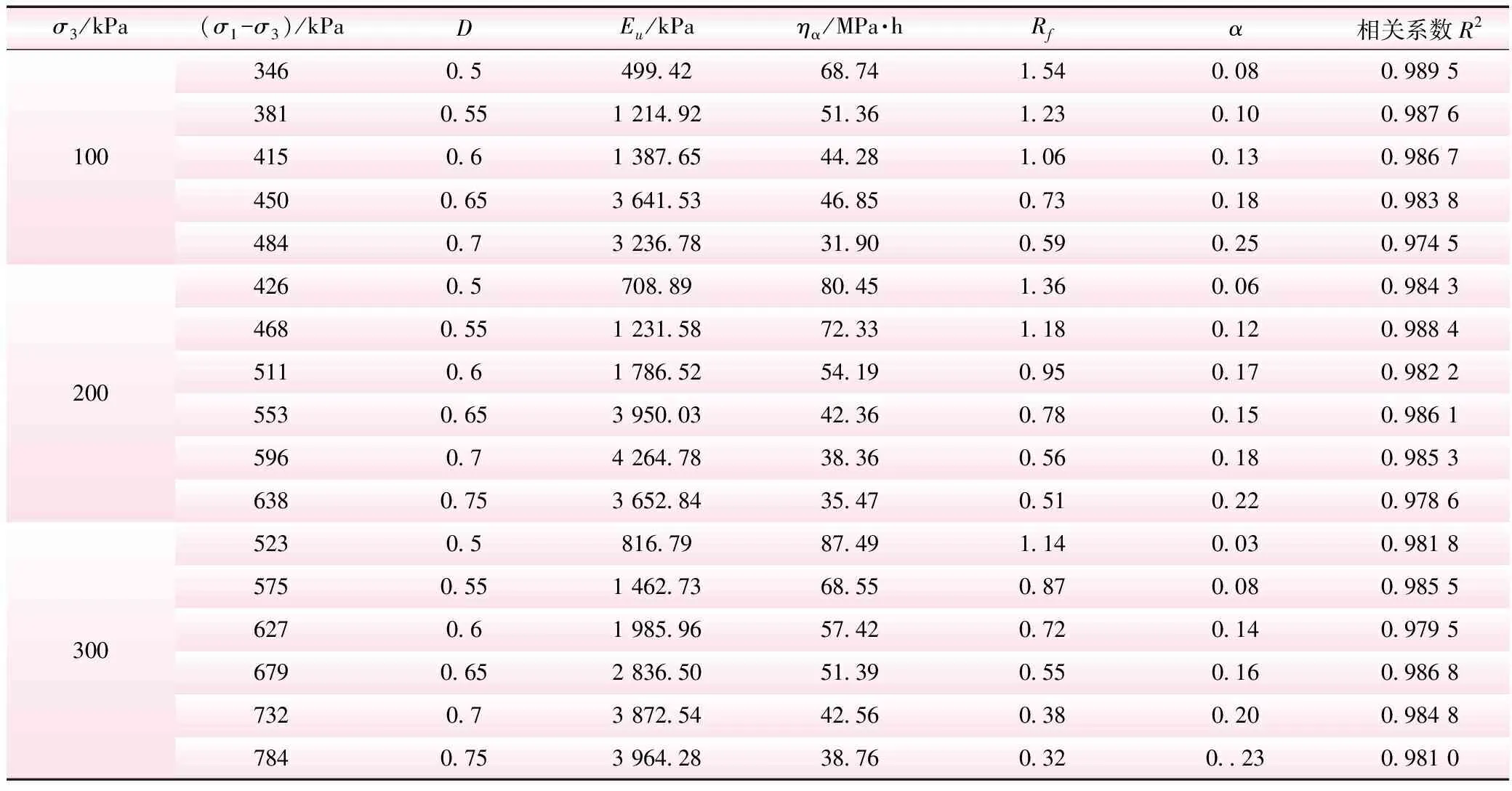
表3 模型参数
从图6可看出,引用经验模型对稳定蠕变阶段的拟合偏差较大,拟合精度相对较低,平均相关系数R2仅有0.947 6。而本文建立的模型对衰减蠕变阶段和稳定蠕变阶段的辨识更为精准,平均相关系数R2达到0.983 9。传统Mesri经验模型属于传统经验模型,具有很强的针对性,仅针对某一种土体,难以推广。而本文建立的模型在传统经验模型的基础上,通过分数阶微积分描述应变-时间关系,从而得到新的分数阶经验模型。该模型参数具有一定的物理意义,模型内涵较为丰富,可从某种意义上表征土体蠕变过程的内在性质,具有一定的推广价值。
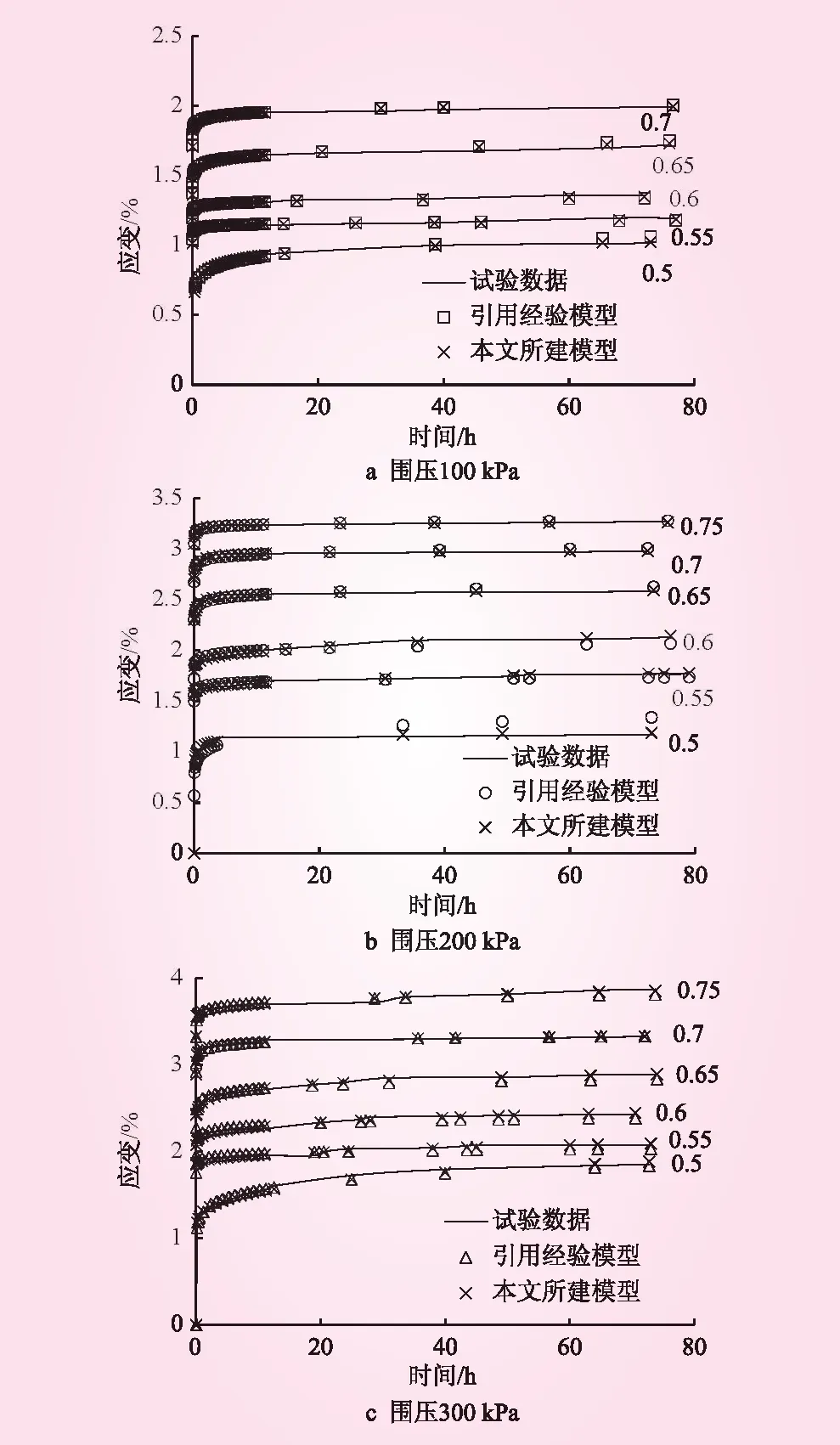
图6 理论值与试验值对比
为验证本文所建模型描述土体蠕变力学性质的适用性,引用文献[17-18]中黄土、高含盐细砂土的蠕变数据,利用本文所建模型进行模拟辨识,得到的理论值与试验值对比曲线见图7。从图7可看出,本文模型对黄土、高含盐细砂土蠕变曲线具有较强的辨识能力,平均相关系数R2分别为0.991 5和0.986 3,理论值和试验值吻合较好。由此证明,本文建立的经验模型能较好地描述土体蠕变力学行为,具有一定的适用性。

图7 理论值与试验值对比
由于元件模型的参数多具有明确物理意义,辨识不同种类、区域的土体蠕变时每个参数表现出不同的规律,故土体元件模型在蠕变模拟中应用更为广泛。经验模型一般仅针对某种土体,本文在传统Mesri经验模型的基础上,保留原有双曲线方程描述应力-应变关系,引入分数阶微积分理论反映土体应变-时间关系,使得改进后的经验模型具有一定的物理意义,突破传统经验模型拟合参数无意义的限制,从某种程度上能体现土体蠕变过程的内在性质,为蠕变经验模型的深入研究提供一种新思路。但是,经验模型如何借鉴元件模型的优点,通过一组或多组参数的差异反映土体性质的规律性差异,这是接下来研究的重点。
5 结 语
滑带土蠕变变形过程中,应变包含瞬时弹性应变和蠕变应变,其中蠕变应变表现出明显的非线性特征,滑带土等时应力-应变曲线近似双曲线。本文在传统经验模型的基础上,保留原有双曲线方程描述近似双曲线形态的应力-应变关系,引入分数阶微积分理论反映土体应变-时间关系,得到改进后的蠕变经验模型。利用所建模型对滑带土、黄土和高含盐细砂土蠕变数据进行辨识,理论曲线与试验曲线较为吻合,拟合精度较高,证明本文模型具有一定的可行性和适用性。
