基于强度双折减理论的粉土边坡稳定性研究
2021-06-11孙玉琢李明宝
孙玉琢,李明宝
(东北林业大学土木工程学院,黑龙江 哈尔滨 150040)
0 引 言
边坡稳定性分析的研究方法多为传统强度折减法,即采用相同的折减系数对边坡土体的强度指标黏聚力c和内摩擦角φ进行折减。随着边坡研究的不断深入,有学者提出了强度双折减的分析方法,认为土体的强度参数c、φ在土体破坏过程中的衰减进程是不同的。干湿循环对土体产生的力学特性的影响是不可逆的,是导致山体滑坡灾害的主要因素之一,降雨会导致地下水位的升高,而在旱季高温作用下水位将有所下降,土体经历过频繁的干燥蒸发以及降雨入渗引起地下水位波动,在此干湿循环因素的影响下土体必然产生形变、强度等物理力学性质的变化。Rayhani等[1]认为,干湿循环导致土体产生裂隙,由此导致强度衰减,并对此进行了试验验证,揭示的土体干湿循环机理变化对工程应用具有重要价值;邓志永[2]通过直剪试验分析了湖南某重塑粉质黏土的抗剪强度在干湿循环条件下的相关变化规律;孙德安等[3]研究了干湿循环作用下膨胀土的抗剪强度特性以及土水特征曲线和微观结构的变化规律。
关于重塑粉土在干湿循环条件下变化规律的相关研究并不是很多。经典强度折减法认为,c、φ具有相同的安全储备,以此为前提确定安全系数。Taylor在莫尔圆分析法中设定c、φ的安全系数不同,认为滑坡产生时,滑动面上的摩阻力首先发挥作用,然后黏聚力加以补充[4],这从一定程度上体现土体强度指标在衰减过程中是有差异的。唐芬等[5]提出了双折减系数法,该方法更符合边坡破坏是渐进过程的规律,为边坡稳定性研究提供新思路。袁维等[6]通过建立c、φ的配套折减原则,说明双安全储备系数的边坡整体安全系数方法是可取的。白冰等[7]从理论方面对比经典强度折减法与强度双折减所得安全系数的大小,建议采用双折减法研究边坡稳定性。陈力华等[8]通过算例分析了有限元方法中边坡失稳三种判据存在的差异,提出了拉剪强度同等折减的强度折减法。丁参军等[9]提出了边坡稳定性分析方法的趋势,指出高等本构模型将作为研究重点,同时要结合新的数学理论应用研究。
以上研究并未以粉土为研究对象,本文模拟粉土在干湿循环条件下强度指标的变化规律,研究c、φ各自的折减特性,通过室内直剪试验得到不同干湿循环次数后粉土的应力-应变曲线和强度参数变化规律,提出了干湿循环条件下土体强度公式,通过ANSYS有限元分析程序,对粉土边坡进行干湿循环状态下的稳定性进行研究,可供粉土边坡的稳定性分析参考。
1 试验用土及试验方案
1.1 重塑粉土的基本物理指标
粉土的工程性质特殊,其类型处于黏性土和砂性土之间,结构性及水理稳定性较差。在我国,将粉土定义为粒径大于0.075 mm颗粒质量不超过总质量的50%,且塑性指数Ip≤10的土。本文试验用土取自黑龙江某边坡,粉土的基本物理指标见表1。

表1 基本物理指标
1.2 干湿循环模拟
根据SL 237—1999《土工试验规程》规定,设置平行试验来提高试验结果的准确性。本次试验共3组,包含2组平行试验,每组制备共24个试样,每4个试样经历同样的循环次数,通过直接剪切试验绘制应力-应变关系图,得到重塑粉土的抗剪强度指标,取平行试验结果的平均值作为试验最终结果。
按照天然状态下,将重塑粉土配成含水率为20.5%的试验土样,闷料24 h以确保水分在土样中均匀分布。选用直径61.8 mm、厚20 mm的标准尺寸环刀,将闷料完成的粉土试样分层装入标准环刀内,控制试样密度为1.83 g/cm3。在制备完成的环刀土样下部垫一层滤纸,并一同放在透水石上,保证水可以入渗至环刀试样中且保留土颗粒不至于外渗。向装有环刀土样、滤纸和透水石的托盘中加水至环刀中间位置,严禁水没过环刀。试样的饱和过程采用浸水的方式,干燥的过程借助试验室烘箱完成,烘箱温度控制在35 ℃。参考时间控制法[10-13]进行干湿循环试验,通过测定试验过程中试样的质量变化,确定饱和与干燥时间。加湿过程初期测量的时间间隔为30 min,随着试样含水率临近饱和含水率28.23%,此时缩短测量试样的测量时间间隔,反复测量最终得到饱和时间。烘干过程所需时间的确定采用同样的测量方法。
试样浸泡12 h,含水率即可达到26%以上,已经很接近饱和含水率。试样在试验室烘箱35 ℃温度下烘干6 h,可使试样含水率大致达到天然含水率20.3%。依据上述试验方法所确定的试验加湿与干燥时间,进行系列干湿循环过程模拟。
1.3 直接剪切试验
采用SDJ-Ⅱ型三速电动等应变直剪仪,量力环系数C=1.910 kPa/0.01 mm,选用固结快剪的试验方法。试验时,每4个试样为1组,对试件分别施加50、100、200、400 kPa的四级垂直荷载,试样剪切采用电动马达驱动。试样以及传力装置安装调零之后,以0.8 mm/min的速率对试样进行剪切并进行周期性记录,对所得数据按照试验规定方法绘制应力-应变曲线,得到不同荷载下粉土的抗剪强度曲线。计算公式为
ΔL=20n-R
(1)
τ=CR
(2)
式中,ΔL为剪切位移;n为手轮转数;R为测力计百分表读数剪应力;τ为剪应力;C为量力环系数。
2 试验结果与分析
整理试验数据,得到不同循环次数下试样剪应力与剪切位移关系,见图1。从图1可知,不同垂直荷载下的剪切位移变化过程不同,相同垂直荷载作用下,曲线强度峰值随着循环次数的增加有所降低,说明干湿循环对粉土强度产生了劣化作用。不同干湿循环次数下所得到的强度指标黏聚力和内摩擦角分析结果见表2。随着干湿循环次数的增加,黏聚力和内摩擦角均有所降低,但两者的衰减进程并不相同。在前6次干湿循环中,黏聚力和内摩擦角的衰减幅度较大,循环至8次时强度指标到达稳定值。试验结果表明,干湿循环对粉土的黏聚力的影响比较明显,折减幅度达30%。随着干湿循环次数的增加,内摩擦角衰减的程度大致为12%。
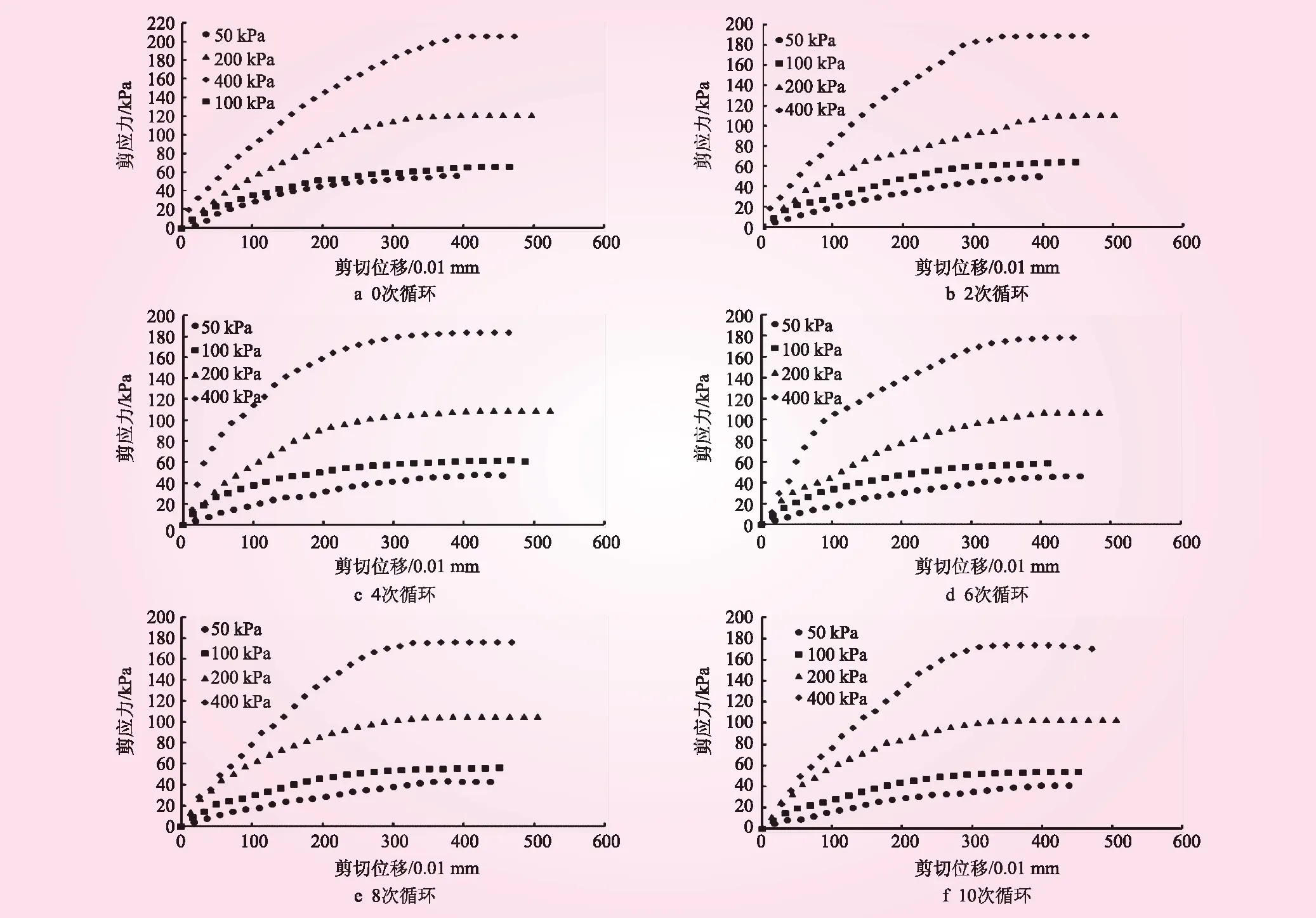
图1 试样剪应力与剪切位移关系
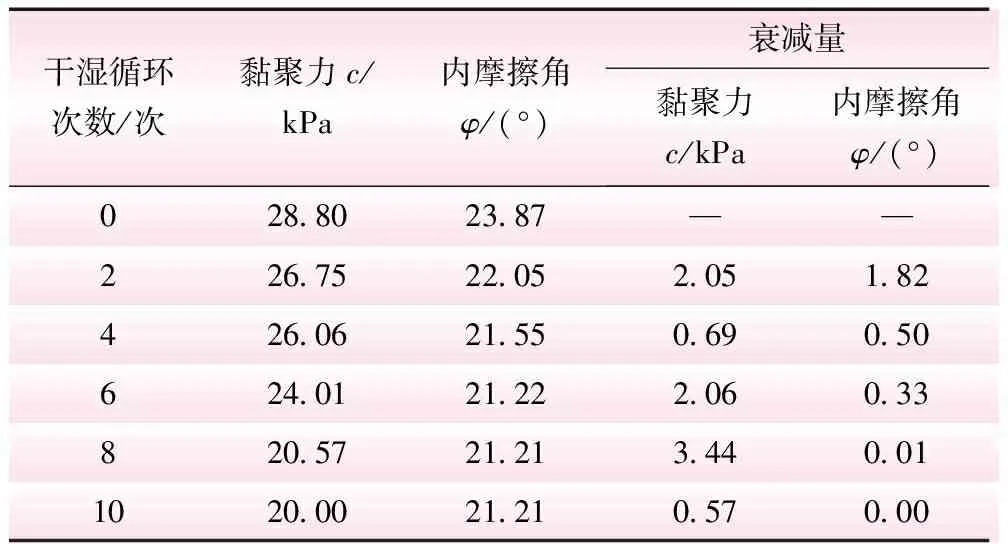
表2 粉土强度参数分析结果
3 双折减路径的确定
依据上述所得试验结果,基于Mohr-Coulomb强度准则,针对试验数据,采用幂函数形式对试验结果进行数据拟合,结果为
τ=c+σtanφ
(3)
φ=23.34n-0.05
(4)
c=29.88n-0.16
(5)
式中,n为干湿循环次数;τ为土体抗剪强度;σ为法向压应力。结合式(3)、(4)和(5)可得
τ=29.88n-0.16+σtan(23.34n-0.05)
(6)
虽然黏聚力与内摩擦角的衰减机制不同,但两者之间依然存在相应联系。本试验中粉土黏聚力与内摩擦角的折减路径可表达为
(7)
式中,Fφ为内摩擦角的折减系数;FC为黏聚力的折减系数。
对比传统强度单折减的计算方法,本文采用的双折减机制具有更明确的物理意义,更加符合土体在天然状态下强度衰减途径。为了验证本文所提出折减方式的正确性,运用有限元仿真程序进行验证。
4 粉土边坡稳定性分析
4.1 干湿循环机制下边坡稳定性分析
建立ANSYS边坡模型,将不同干湿循环次数下边坡土体强度指标编入程序中,得到相应的模拟结果进行边坡稳定性分析。不同循环次数下边坡坡顶X方向的位移云图见图2。从图2可知,干湿循环引起土体强度衰减,进而导致了边坡产生形变,产生最大位移的位置在坡顶,并随着边坡土体强度的进一步衰减,边坡土体向坡脚移动,坡脚形变随之增加。边坡模型在0、2、4、6、8、10次循环后,边坡坡顶在X方向的位移分别是57.99、52.74、48.82、42.57、37.35 mm和31.99 mm。从边坡位移的角度看出,随着循环次数的增加,边坡坡顶最大位移逐渐减小,并且变化幅度逐渐减弱,边坡稳定性逐渐降低。
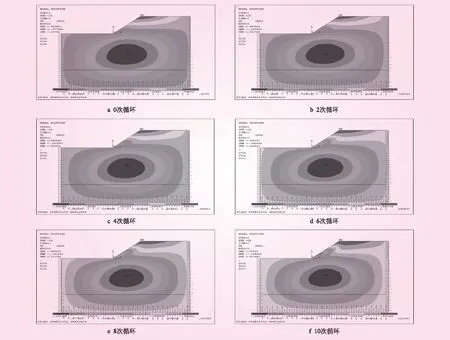
图2 不同循环次数下边坡坡顶X方向的位移云图
不同循环次数下的边坡塑性应变云图见图3。从图3可知,边坡失稳是一个渐进的过程,塑性区由坡脚产生,随着边坡土体进一步衰减,塑性区呈圆弧状由坡脚向坡顶逐渐扩展。未循环前,边坡的塑性应变为0.237,随着干湿循环次数的增加,边坡的塑性应变相应增加,直到第8次循环结束,边坡的塑性变形达到0.843,继续干湿循环至第10次结束,边坡模型的塑性应变值略有下降,为0.711。边坡模型的塑性变形量的增加使得边坡稳定性降低,边坡中的塑性区由坡脚逐渐向坡顶扩展,随着干湿循环次数的增加,圆弧状的塑性区到达坡顶,边坡破坏。
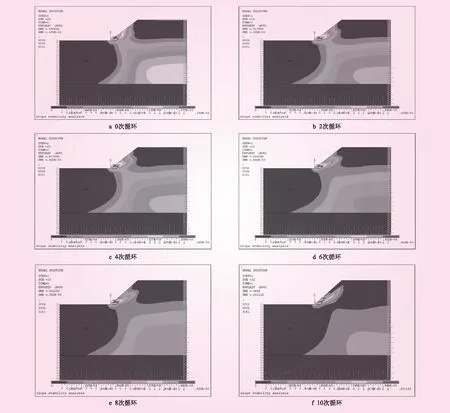
图3 不同循环次数下的边坡塑性应变云图
4.2 双折减路径方法与传统折减方法对比
通过对粉土进行室内试验,得到粉土在干湿循环条件下的折减机制,将该机制编入ANSYS有限元分析程序中,对粉土边坡进行模拟。边坡达到破坏时的坡顶位移云图与边坡的塑性应变云图见图4。从图4可知,边坡破坏时的破裂面呈圆弧状,塑性区由坡脚产生,坡顶土体向坡脚挤压,当塑性区贯通时边坡失稳形成滑坡。边坡稳定性计算结果表明,同步折减法的安全系数为1.39。按照本文提出的双折减路径所得的安全系数为1.35。通过对比,说明传统强度折减法高估了边坡的稳定性,强度双折减方法更为精确,采用双折减法更符合实际粉土强度衰减的情况。
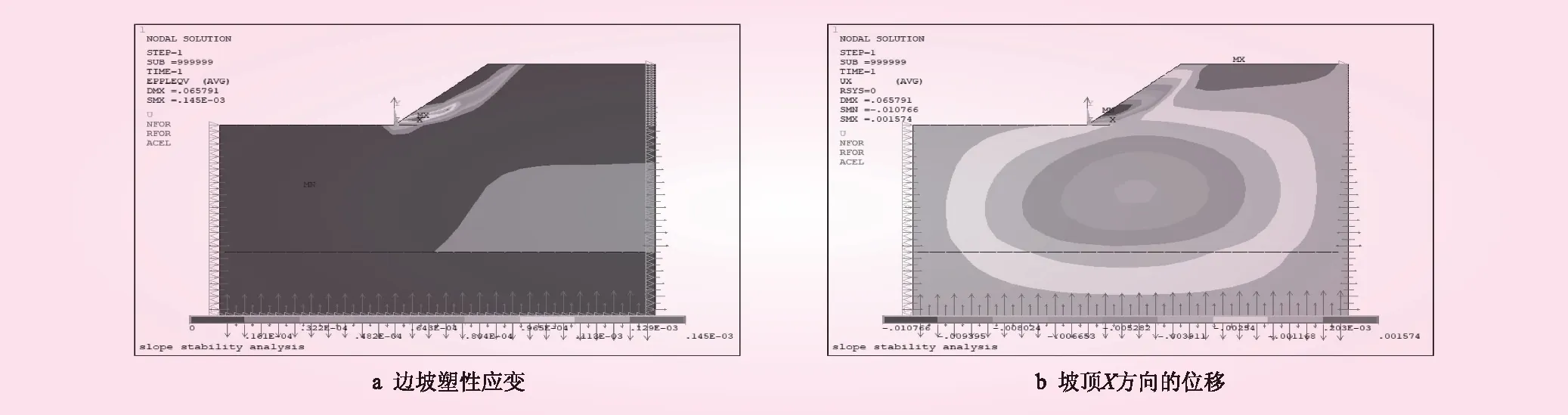
图4 边坡破坏时数值模拟云图
5 结 语
本文基于强度双折减理论,对粉土边坡稳定性进行了研究,得出以下结论:
(1)粉土的强度指标随着干湿循环次数的增加,各自衰减的速度并不相同。相比内摩擦角,黏聚力的衰减受干湿循环的影响更加明显,随着干湿循环次数的增加,黏聚力的衰减速度逐渐减慢,并趋于平稳。
(2)由于粉土强度指标各自的折减特性不同,通过干湿循环试验所得粉土强度指标的衰减特性具有实际物理意义,得出干湿循环条件下土体强度公式。采用有限元分析程序对粉土边坡进行干湿循环状态下的稳定性分析表明,随着循环次数的增加,边坡坡顶位移量逐渐减小,边坡塑性区由坡脚产生并逐渐向坡顶扩展。干湿循环次数的增加会导致粉土边坡稳定性的降低。
(3)干湿循环是导致土体强度衰减的重要因素,经过与传统强度折减法的对比可知,传统强度折减法在一定程度上高估了边坡的安全性,双折减法的折减机制更符合土体实际的劣化过程。
