低空接敌战术对机载雷达探测能力影响分析

常一哲，李战武，徐 安，徐宝伟，杨爱武，刘 帅

（1.空军工程大学航空工程学院，西安710038；2.解放军94638 部队，南昌330201；3.空军石家庄飞行学院理论训练系，石家庄050081；4.北部战区空军保障部，沈阳110066）

0 引言

随着机载雷达技术的发展，作战飞机对空中目标的探测能力有了极大的提升。在此背景下，在空战中如何避免目标被发现成为各国关注的重点。针对该问题，业界主要从技术和战术两方面进行研究。在技术层面上，利用作战飞机的隐身技术可以有效降低载机的被探测概率；在战术层面上，则可利用战术战法、自然环境等因素削弱目标对载机的探测能力，其中的典型战术就是利用目标机载雷达的多普勒盲区进行接敌。这种战术机理是在现有空战条件下，双方战斗机的机载雷达普遍采用脉冲多普勒（Pulse Doppler，PD）体制，依据目标运动的多普勒效应，在频域中完成杂波背景下的目标检测［1-4］。但是，载机与目标的相对运动变化会引起杂波多普勒谱的扩展，导致机载雷达在搜索低空、超低空目标时会出现多普勒盲区［5-6］，从而在理论上为载机的低空隐蔽接敌提供了支持。

对于目标处于低空飞行条件下的雷达探测能力问题，诸多专家学者进行了分析研究。文献［7］针对探测低空突防的巡航导弹问题，计算得到导弹在不同高度、不同杂波条件下突防时雷达的探测概率。文献［8］针对预警机在不同杂波条件下的探测能力进行了分析，计算得出了信噪比与噪声的关系。文献［9］考虑到目标的动态起伏性，建立了对应的探测概率计算模型，计算出了不同条件下的目标探测概率。在既有成果中，以空战为背景，探测对象为歼击机的研究较少，且对于空战战术战法研究的借鉴意义不足。

本文针对该问题，以空战为背景，分析研究了低空接敌这一战术对机载雷达探测能力的影响。首先对低空接敌的战术机理进行了简要介绍；之后针对该战术战法，建立对应的数学模型进行描述；其次给出了论文所提出的分析方法的具体流程；最后采用了具体算例进行仿真，验证了在不同作战环境、不同杂波条件下的低空接敌战术对机载雷达探测能力的影响。

1 模型建立

针对本文所研究的具体问题，从机载雷达探测概率、地杂波功率、目标回波功率、典型飞机RCS 等方面分别建立数学模型。

1.1 雷达发现概率模型

本文从机载雷达累计发现概率和单次发现概率两方面给出其模型。

1.1.1 累计发现概率模型

1.1.2 单次发现概率模型

本文的作战背景想定为载机采用低空接敌的战术对目标机载雷达探测概率的影响，因此，考虑到载机的RCS 分布特性，应采用Swerling IV 型起伏模型对目标机载雷达的探测能力进行描述［11］。基于此，给出雷达单次发现概率Pd模型如式（2）所示［12］：

式（3）中，VT为检测门限，可以通过Newton-Raphson方法中的递归公式近似得到。

1.2 综合信噪比模型

根据文献［10］，雷达接收机接收到的信噪比SNR 定义为：

式（4）中，Pr为被探测目标回波信号功率；Pn为接收机内部噪声功率。

而在杂波环境下，考虑到环境杂波对雷达作用能力的影响，其SNR 模型修正为SIR 模型，即为：

式（5）中，Pc为地杂波功率；I 为杂波改善因子。

1.2.1 被探测目标回波信号功率Pr模型

根据文献［13］，给出被探测目标回波信号功率Pr模型，如式（6）所示：

式（6）中，Pt为雷达发射功率，G 为天线增益，λ 为雷达工作波长，R 为雷达与目标间的距离，L 为雷达系统损耗，σ 为载机RCS，其模型在下文中建立。

1.2.2 地杂波功率Pc模型

根据文献［12］，给出地杂波功率Pc模型，如式所示：

式（7）中，σc为地杂波强度，其模型在后文建立。

1.2.3 雷达接收机内部噪声功率Pn模型

根据文献［12］，给出雷达接收机内部噪声功率Pn模型，如式（8）所示：

式（8）中，k 为波尔兹曼常数，Fn为接收机噪声系数，T0为系统噪声温度，Bn为接收机等效噪声带宽。

1.3 动态RCS 模型

由于各国战机的RCS 数据高度保密，因此，本文选取网络已公开的某型飞机RCS 数据进行分析。RCS 计算方法为MOM 法，电磁波为X 波段，频率10 GHz，极化方式为垂直极化，计算得到结果如图1所示［13］：

图1 某型飞机三维RCS 模型

根据雷达入射角度为360°×360°范围的载机RCS 数据，将载机的动态RCS 模型定义为关于雷达电磁波入射角度的函数，即：

式（9）中，φ 是雷达电磁波的入射方位角，φ 是雷达电磁波的入射俯仰角。

1.4 地杂波强度σc 模型

雷达接收到的地杂波主要是陆地表面对电磁波的散射形成的，其强度由雷达分辨单元面积和杂波后向散射系数共同决定。

首先给出地杂波强度σc的定义：

式（10）中，As为雷达分辨单元面积，其模型为：

式（11）中，c 为电磁波传播速度，为雷达发射脉冲宽度，θβ0.5为雷达波束俯仰半功率宽度。

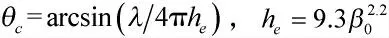
表1 地杂波Morchin 模型参数

2 分析流程

根据以上模型，可以给出低空接敌对机载雷达探测能力影响分析的具体流程，如图2 所示。

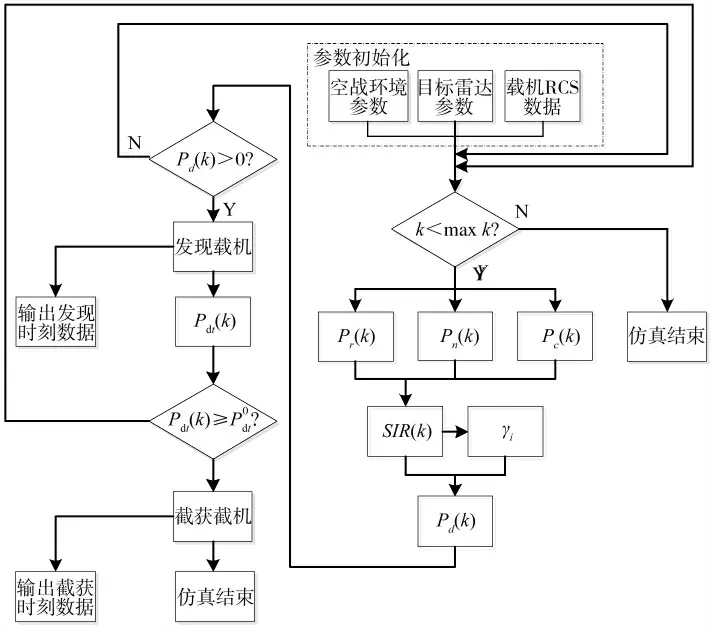
图2 低空接敌战术对机载雷达探测能力影响分析流程

3 仿真分析

为了充分验证本文所提方法的可行性，选取不同作战环境下的空战算例进行分析验证。在算例仿真中，选取目标发现载机和截获载机两个关键事件的相关信息作为低空突防效果分析的评判指标。

3.1 算例1

假设载机与目标在沙漠环境中遭遇，目标开启机载雷达进行搜索，仿真基本参数设置如表2所示。

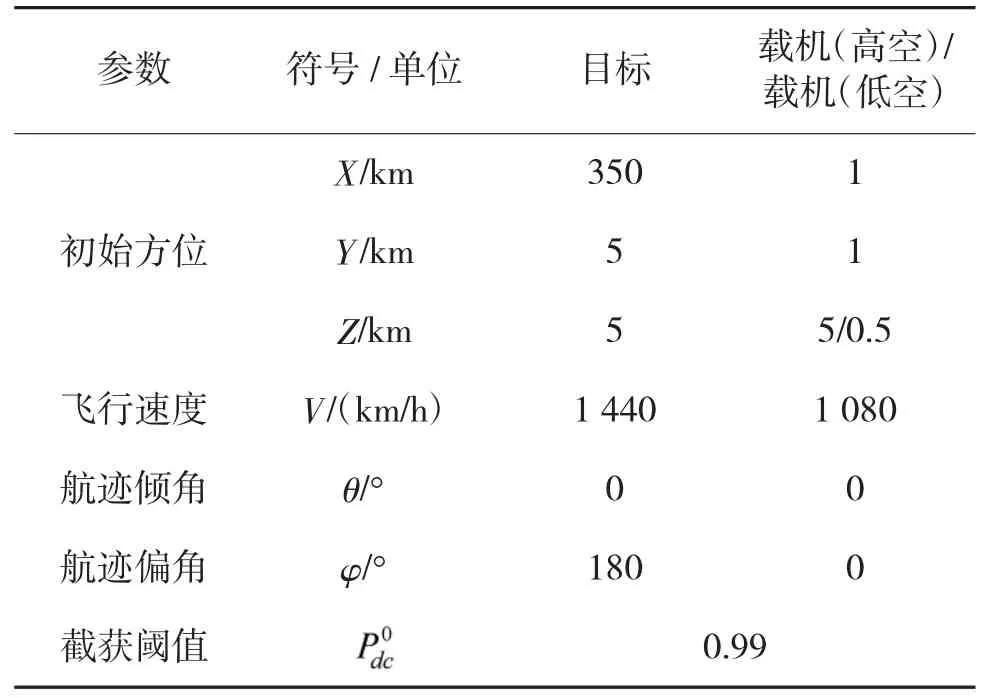
表2 基本参数设置

目标雷达参数设置如表3 所示。

表3 目标雷达参数设置

杂波参数设置如表4 所示。

表4 杂波参数设置

根据以上信息，得到载机与目标的运动初始态势，如图3 所示。

在此态势下，计算得到目标雷达对高空和低空下载机的发现和截获两个关键事件的时间和相对距离信息，如表5 所示。

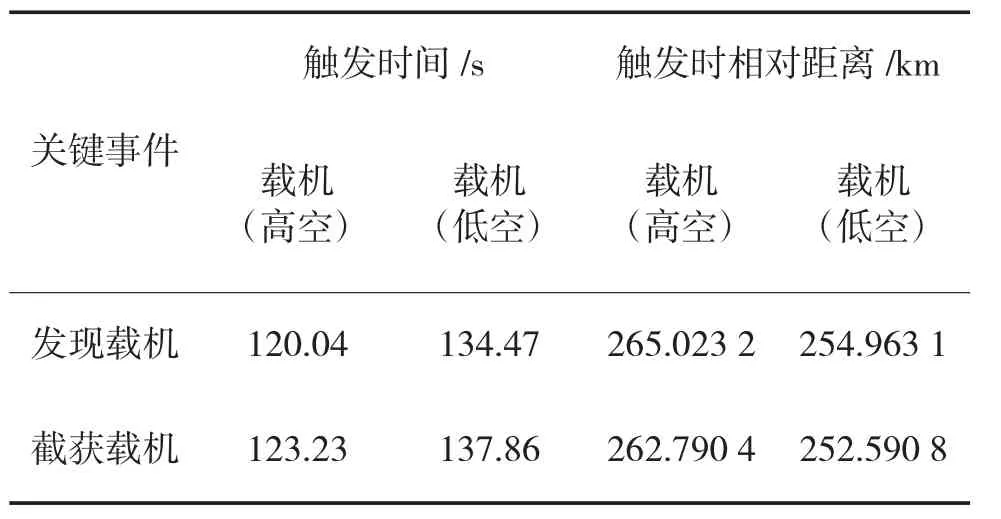
表5 关键事件相关信息统计

累计截获概率随时间变化的趋势如图4 所示。

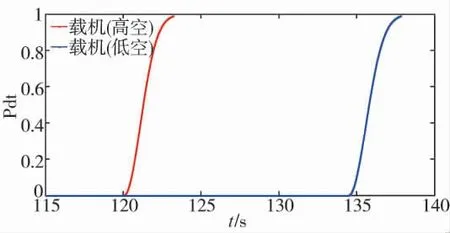
图4 载机处于不同条件下目标雷达的累计截获概率

从表5 和图4 可以看出，在不同飞行高度条件下，无论是对载机的发现还是截获，触发时间和触发相对近距离两项指标都发生了巨大变化。在低空时，目标机载雷达对载机的发现时间相比在高空时提前了14.43 s，发现距离缩减了10.060 1 km，而截获时间则对应提前了14.63 s，距离缩减了10.199 6 km。由此不难发现，采用低空接敌并借助地杂波的掩护，能够有效降低目标雷达的探测能力。

3.2 算例2

假设载机与目标在丘陵环境中遭遇，目标开启机载雷达进行搜索，仿真基本参数设置中载机的高度在高空和低空分别调整为2 km 和6 km，目标的飞行高度为5 km。由此得到载机与目标的运动态势，如图5 所示。

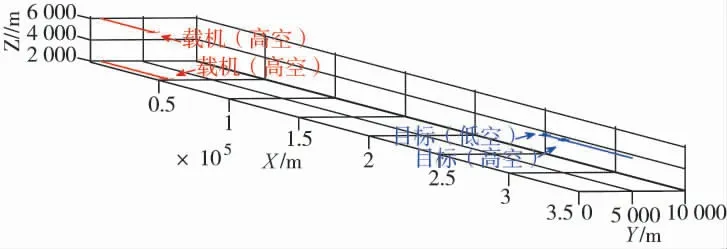
图5 载机与目标的运动初始态势

在此态势下，计算得到目标雷达对高空和低空下载机的发现和截获两个关键事件的时间和相对距离信息，如表6 所示。

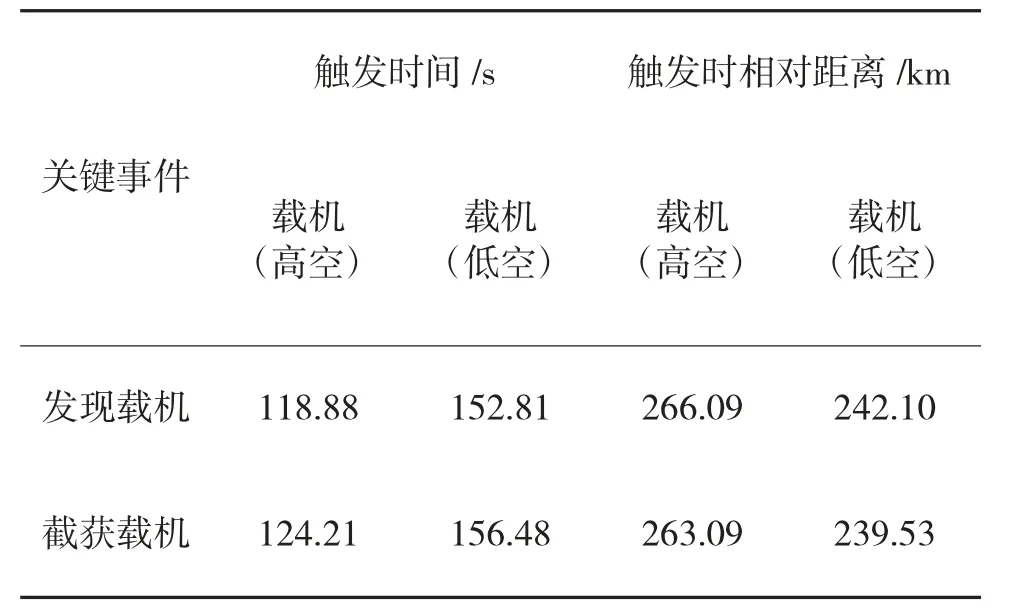
表6 关键事件相关信息统计

图6 载机处于不同条件下目标雷达的累计截获概率

累计截获概率随时间变化的趋势如图6 所示。

对表6 和图6 进行分析，可以发现在沙漠环境中地杂波同样对机载雷达的探测能力产生了巨大影响。在载机处于低空相比于处于高空的条件下，目标机载雷达的发现时间由118.88 s 推延至152.81 s，延迟了33.93 s；发现距离则由266.09 km 缩短至242.10 km，缩短了23.99 km；截获时间则由124.21 s推延至156.48 s，延迟了32.27 s；截获距离则由263.09 km 缩短至239.53 km，缩短了23.56 km。通过该算例可以看出，地杂波能够有效降低机载雷达的搜索跟踪能力。

以上两个仿真算例的结果表明，在不同的环境下，低空接敌战术对目标雷达探测能力的影响程度不同。但是在任意一种环境下，该战术都能够依托地杂波的掩护在一定程度上削弱机载雷达的探测能力。因此，也证明了在空战中，低空接敌的战术是降低目标雷达探测能力的有效手段。

4 结论

本文针对低空接敌战术对机载雷达探测能力的影响问题进行了分析研究。首先依据脉冲多普勒雷达的体制，从定性的角度探讨了该战术战法的机理；其次从雷达、杂波、RCS 等几个方面分别建立了数学模型；之后以流程图的形式给出了分析流程的具体描述；最后针对两种不同环境下的空战场景，通过仿真验证了低空接敌战术在不同环境下对机载雷达探测能力的影响程度。

通过本文的研究可以看出，低空接敌战术能够有效降低机载雷达的探测能力，为空战战术战法的研究奠定了理论基础。