基于粒子群算法的装备预防性维修策略研究
2021-06-11王永虎焦敬义于博文
王永虎,焦敬义,于博文
(1.武警工程大学研究生管理大队,西安 710086;2.武警工程大学装备管理与保障学院,西安 710086;3.武警宁夏总队参谋部,银川 750001)
0 引言
随着实战化军事训练的持续深入推进,装备使用强度、使用时长和环境应力较以往有了明显增强,装备损耗、需求和维修矛盾日益凸显。因此,针对新形势下实战化军事训练实际,加强对装备维修保障的科学预测和定量分析,提高装备维修精确化,发挥装备最大使用效益十分必要。
目前,国内学者在立足我国装备维修管理实际的基础上,吸收改进国外先进维修理念,在维修策略研究方面取得了一些成果。高萍[1]在综合考虑复杂设备特点及其维修方式的基础上,建立了复杂设备功能单元重要度评估指标体系,以可用度和维修费用为约束条件建立了计划维修周期模型,为维修方式决策提供了可靠依据。王刚等[2]利用信息系统收集的动态信息,考虑舰船电子装备维修保障过程中的决策指标,提出了一种动态维修决策的优化模型。王亮[3]以某型坦克分系统为研究单元,以可用度为约束条件、费用最小为目标建立优化模型,利用遗传算法和蒙特卡洛方法,得出了最佳预防维修周期。喻刚等[4]将RCM 方法应用于装备维修中,通过分析故障模式的影响,确定装备维修内容,研究制定维修策略。赵英俊等[5]以装备监测周期为约束、以维修费用率最小为目标函数,研究建立防空反导装备维修决策优化模型。金保平等[6]考虑了多维修模式的港机维修策略,基于粒子群算法得到了港机装备有限运行时间内的维修模型。肖雨等[7]着眼保障任务成功,研究了以成功概率最大为目标的装备维修策略模型。王强等[8]针对战时装备受到使用退化与随机冲击的共同作用发生竞争失效的问题,提出了基于状态的预防性维修策略。王谦等[9]在考虑不完全预防性维修的基础上,把厂家和用户的预防性维修进行组合,以保修费用为研究对象,建立降低保修费决策模型。
分析当前维修策略研究方向可以发现,在实战化军事训练背景下,如何有效解决高强度使用造成的装备损耗严重和保持较高装备完好率之间的矛盾相关研究较少。结合任务实际,提出加大预防性维修力度,通过建立数学模型,科学预测装备在服役期内的最优预防性维修次数和时间间隔,提高装备保障效能。
1 模型描述
装备维修方式主要有事后维修、预防性维修、状态维修、改善维修等,由于军队装备具有军事属性,对装备可靠度要求较高,必须时刻保持较高完好率,因此,在维修保障方面应重点考虑预防性维修方式,以保持装备具备较高的完好率。
预防性维修是为了防止装备性能、精度劣化或降低,按事先规定的计划和相应的技术要求所进行的维修活动。随着装备技术性能的不断提高,以及军队人装结合实战化训练的不断推进,军队对装备的依赖度与日俱增。同时由于大部分装备的高技术性、精密性以及复杂性,使得装备维修的时间消耗越来越长、经费投入越来越高,因此,提高预防性维修能力对于军队具有军事和经济双重效益。
构建装备维修模型,通常将装备生命周期划分为若干段,引入役龄回退因子对装备服役时间进行修正。综合考虑装备可靠性和经济性等约束条件来优化维修模型,得到装备在有效时间内的最优预防性维修次数和维修时间间隔,可有效提高装备完好率,节约装备维修成本。
2 模型假设条件
2.1 装备故障率分析
在建立装备预防性维修策略优化模型前,首先需要通过可靠性分析和寿命检验理论得出装备故障率分布函数。可靠性其数量指标就是可靠度,记为R(t),相对应的是不可靠度,即产品的寿命分布函数,记为F(t)。则:

t 时刻单位时间内的故障概率记为f(t),则:

根据可靠性、寿命分布函数和寿命分布密度函数的定义,则:

同时,装备的失效分布类型在可靠性理论中是一个重要的研究问题。常见的装备失效分布一般服从指数分布、正态分布、伽马分布、对数正态分布、威布尔分布和极值分布等[10],因某一局部失效而导致全局停止运行的元件、部件、器件、设备等的寿命都可以看作服从威布尔分布,机械中的疲劳强度、疲劳寿命、磨损寿命、腐蚀寿命大多服从威布尔分布[11]。因此,本文采用威布尔分布建立装备可靠性模型。威布尔分布的失效概率密度函数为:

式中,m 为形状参数;η 为尺度参数。
由式(4)和式(5)可得

则可靠度函数为:
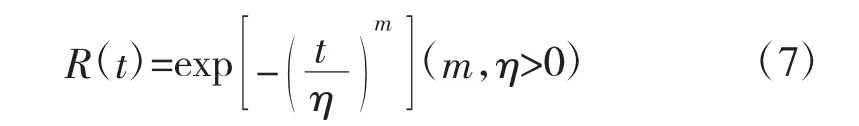
失效率函数为:
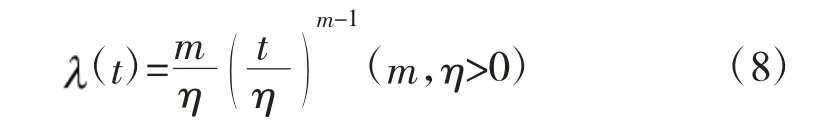
2.2 装备役龄分析
预防性维修可视为不完全维修。预防性维修后,装备的状态或役龄都会发生变化,在此引入役龄回退因子αi修正装备役龄。修正后的装备役龄εi为:

由于受到装备预防性维修成本、(零)部件使用年限、维修时间间隔等因素影响,役龄回退因子是动态变化的,其中预防性维修成本是影响役龄回退因子的主要因素。可用下式表示:

式中,Cpmi为第i 次预防性维修费用,Cpr为装备购置成本,a,b 为调整参数。
2.3 预防性维修模型
假设在装备使用寿命[0,T]区间内,预防性维修次数为n,预防性维修时间间隔为Δti。装备预防性维修的总成本C,主要由预防性维修期间的故障小修成本Ccm和预防性维修成本Cpm两部分组成。假设在第i 个预防性维修期周期内发生意外故障的次数为φi,则:

假设小修的平均成本为Cmin,则装备维修间隔期内的最小维修成本Ccm为:
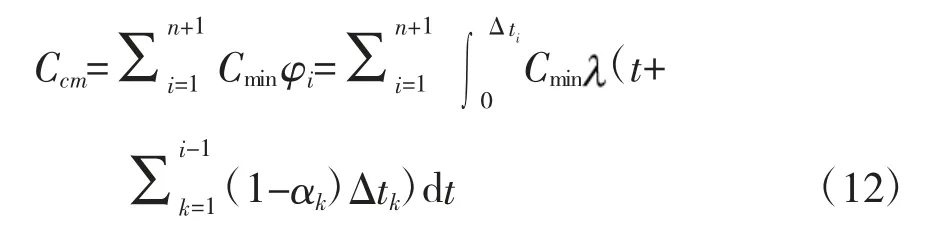
综上所述,装备的综合预防性维修策略优化模型为:
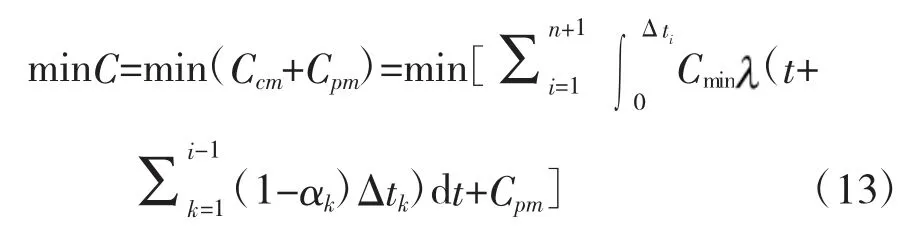
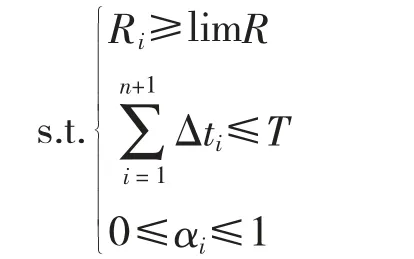
2.4 可靠性模型
装备服役期内,科学地实施预防性维修可有效降低故障发生次数,但过多的预防性维修会导致总维修成本增加,而维修活动不足会提升故障率,增加装备故障维修成本。因此,应科学合理地安排预防性维修的开始时间、时间间隔和次数,使得装备总维修成本最小,可靠性最高。
由式(9)的推导公式,求得R(t):

由于预防性维修后,装备可靠性在不断变化,所以可求得平均可靠性R(t):
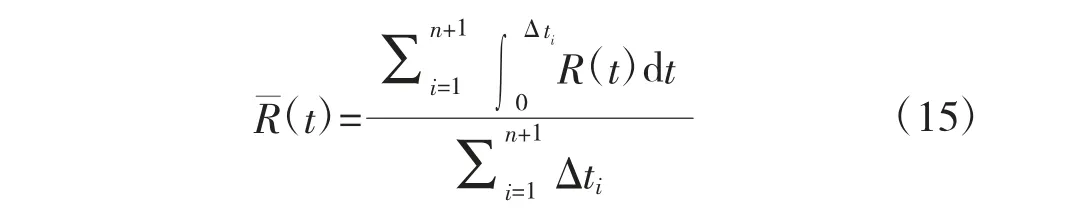
因此,装备的可靠性优化模型为:
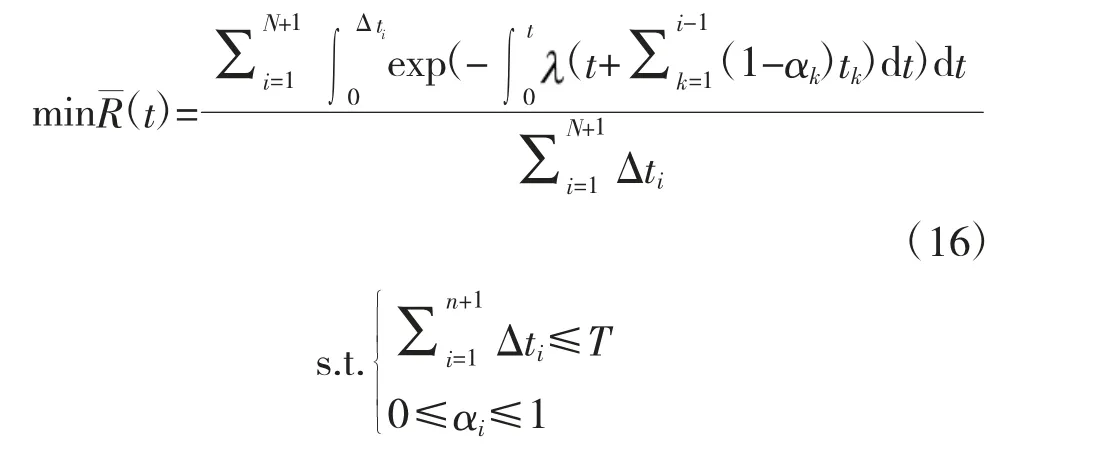
3 基于多目标粒子群算法的模型求解
粒子群优化算法[12](Partical Swarm Optimization,PSO)又称粒子群算法,是由Eberhart 博士和Kennedy 博士于1995 年提出的,它是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法。由于粒子群优化算法具有搜索效率高、通用性好、容易与传统优化方法结合等优点,因此,将粒子群优化算法应用于解决多目标优化问题上具有很大的优势[13]。目前,多目标粒子群优化算法也已成功用于函数优化、神经网络训练、模式分类、模糊系统控制以及其他的应用领域[14]。
粒子群优化(PSO),是基于群体智能协作理论的优化算法,通常用来解决非线性连续函数优化及多目标优化等问题。利用PSO 算法求解的基本思路是,随机产生多个粒子,每个粒子代表研究问题的一个可行解,通过对比取优不断更新粒子适应值,最终求得进化后种群的最优解集。
优化算法的实现步骤如下:
1)初始化参数。设置种群粒子数S=50,随机产生50 个初始解xi(t)和初始速度vi(t)。
2)计算每个粒子的适应度。当前每个粒子的位置和适应值记为pi,种群中最优粒子的位置和适应值记为pg。
3)利用算法,计算每个粒子替换种群最优值的概率。
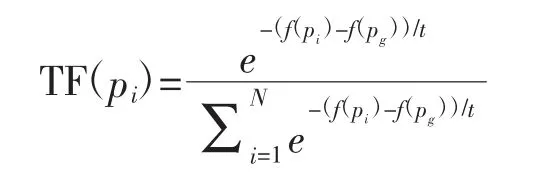
4)更新每个粒子的位置和速度。

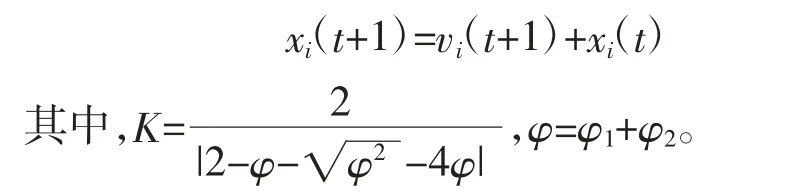
5)将每个粒子适应值与个体极值进行比较,取优更新为个体极值pi和种群极值pg。
6)停止准则判断。最大迭代次数设置为100次,若满足判定条件,则算法停止并输出最优解,否则转到步骤3)。
4 算例分析
为了验证所提模型的可行性和实用性,以某现役装备为维修对象进行算例分析。根据该装备维修数据统计,相关模型数据如表1 所示。

表1 装备维修数据统计
现以预防性维修次数n=5 为例,说明多目标粒子群算法的求解过程。图1 为通过MATLAB 求解得到的随机初代种群。
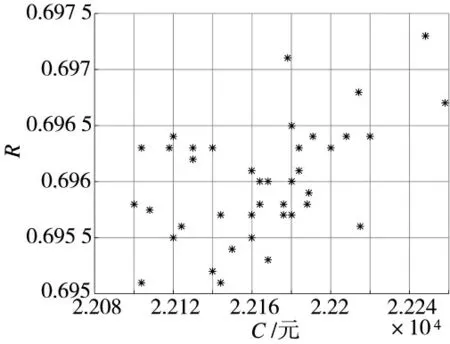
图1 n=5 时的随机初代种群分布
图1 中横轴表示装备的维修成本C(元),纵轴表示对应的装备平均可靠性R。由图1 可知:粒子群初代种群在R-C 平面上分布广泛,只有局部分布密度较小,保证了多样性,从另一方面也说明了初代种群的合理性。

图2 n=5 迭代100 次的最优解

图3 n=5 时的全局最优解
图2 是粒子群迭代100 次的最优解R-C 分布图,图3 为粒子群迭代100 次的全局最优解R-C 分布图。通过对图2 和图3 的比较,可以总结出:全局最优解比迭代100 次的最优解点分布更为优化,并且最优解较多,因此,将全局最优解作为优化结果是最佳选择。

图4 全局最优解整体分布
图4 是装备维修次数n 在[1,10]间的全局最优解的R-C 分布图,从图4 中可得出:当装备维修次数固定时,装备平均可靠性随着维修成本的增加而增高。当n=10 时,装备的R=0.987,可靠性已经很高,所以本文只研究n 在[1,10]的全局最优解。图5为得到的最终的优化结果。

图5 最终优化结果

图6 最终优化结果对比
由于n 在区间[1,2]时,都是较差的维修计划,所以可在后面的分析中排除。图5 显示的是n 在[3,10]之间的维修计划,当维修计划在这个区间时,随着装备维修次数增加,维修间隔时间缩短,而装备的可靠性R 和维修成本C 都有增加。
由图4 可知,当装备维修次数n 在[1,10]之间,维修成本C 的值一直在20 000 元以上,所以C值的改变对结论影响不大。为使结论更加全面且有说服力,可将维修成本C 和服役时间区间T 固定,维修间隔的最小时间Δti取5 h;或将维修成本C 和维修间隔的最小时间Δti固定,服役时间区间T 取[0,1 000]。这样能够得到3 组模型数据,就可以在图5 中进行3 组数据的对比分析,如图6 所示。
分析图6 中的数据可知:C、T 固定,Δti=5 时,由于维修间隔的最小时间缩短,随着维修次数的增加,维修成本上升且可靠性下降;C、Δti固定,T 取[0,1 000]时,由于服役时间区间T 最大值的减小,当维修次数较少时,相同维修成本下的可靠性稍微提高,但是随着维修次数的增加,维修成本上升且可靠性下降。
若决策者以装备维修成本C 为优化目标时,就可选择C 最小的点A(20 545,0.562 1)为最优维修计划,此时,装备的维修成本最低,即C=20 545 元,图7 为图5 的局部放大图。
若决策者需要装备的平均可靠性R>0.8,则可选择图8 中的点B(24 435,0.818 85)为最优维修计划,由于图8 是图5 的局部放大图,所以可知此时装备的维修次数n=7,装备的维修成本为24 435元,可靠性为0.818 85。
若决策者需要装备的可靠性R>0.87 且C<27 000,可选择图9 中的点C(26 061,0.876)为最优维修计划,由于图9 是图5 的局部放大图,所以可知此时装备的维修次数n=8,装备的维修成本为26 061 元,可靠性为0.876。
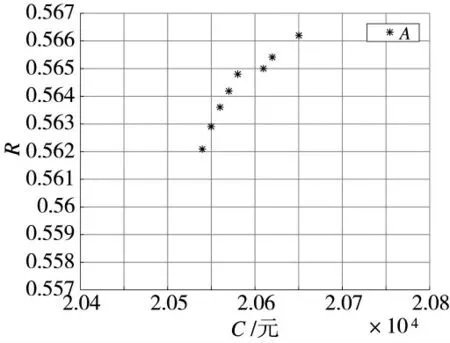
图7 C 的最小点A
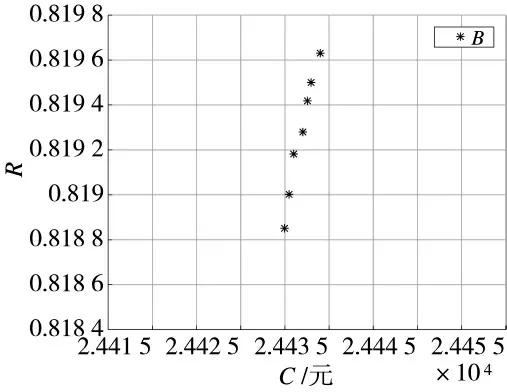
图8 R>0.81 的最优点B

图9 R>0.87 且C<27 000 的最优点C
综上所述,使用多目标粒子群算法求得最终的全局最优解理论上都是最优的维修计划,每种维修计划都在R 和C 之间取了最合理的折衷,决策者可根据实际需求灵活选择不同的维修计划,装备的R和C 都会有所不同。
在装备实际的使用过程中,主要可以分为两个不同的阶段:平时和战时(包括演习)。部队平时训练时,装备人员时常注重保养,所以武器装备的维修成本C 相对较低,就可选择C 最小的点A(20 545,0.562 1)为最优维修计划,使得装备的维修成本最低,即C=20 545 元;部队有演习任务或者处于战时,就会对装备的平均可靠性提出很高的要求,可选择R>0.8,那么图8 中的点B(24 435,0.818 85)为最优维修计划,可靠性高达0.818 85。
5 结论
实战化背景下,传统的维修保障方式已无法满足新的训练形势需要,必须立足实际加大预防性维修力度,来实现装备在高强度训练条件下能够保持较高的战备完好率。本文以预防性维修成本最低为目标函数,以可靠性为约束条件,建立了预防性维修策略综合优化模型,并以某现役装备为例,利用粒子群算法,求解出该装备在服役期内的最佳预防性维修次数和时间间隔,表明了该预防性维修策略优化模型的可行性和实用性,在实际维修保障中有一定的参考价值。
