基于时间序列神经网络的新冠肺炎疫情预测

吴琦琦，黄志甲，周 恒，卞梦园，寇遵丽，张金星

(安徽工业大学建筑工程学院，安徽马鞍山243032)

新冠肺炎是由严重急性呼吸综合征冠状病毒2(SARS-CoV-2)引起的一种传染性疾病。2019 年12 月下旬在武汉首次报道，截至2021 年3 月底，全球累计新冠肺炎确诊病例约12 254 万例，累计死亡病例约270万例，分布在220个国家和地区。新冠肺炎主要通过飞沫、接触、间接接触以及气溶胶等方式传播，临床表现主要为发热、乏力、干咳、呼吸困难和疲倦等症状，严重可导致死亡。新冠病毒传播速度快，给各国家医疗系统带来了巨大挑战。在传染病防控过程中，根据实时监测数据，构建预测模型预知新冠肺炎病例数、预测疾病流行趋势具有重要意义。国内外学者利用权威机构疫情公开数据展开研究，并建立各种不同的预测模型对疫情发展趋势进行预测，这对卫生医疗系统设备的合理调控进行了有效指导。目前，用于新冠肺炎疫情预测的模型和方法较多，主要包括回归模型、传播动力学模型、人工神经网络模型、时间序列模型等。回归模型用于预测某一时刻的值，但在预测早于这一时刻的效果有限；人工神经网络模型具有灵活的非线性函数映射能力，但不能应用于包含线性和非线性的时间序列结构；传播动力学模型依托疫情暴发早期数据可科学预测疫情流行趋势，但由于暴发初期疫情数据的有限性与不完整性，单独应用并开展科学预测仍存在限制；时间序列模型的数据准备和操作执行较简便易行，通常被用来预测传染病的短期波动，但对于罕见且严重程度高的疾病不能很好地模拟，因此同神经网络方法相结合的组合模型被开发。由时间序列预测原理可知，新冠肺炎疫情的发展与时间变化存在一定的相关性，新冠肺炎日累计确诊病例数和日累计死亡病例数是反映疫情变化发展的重要指标。因此，建立基于时间序列的反向传播(back propagation,BP)神经网络模型，使用MATLAB软件进行学习与训练，对2020年2月12日至4月15日全国、武汉市和北京市新冠肺炎日累计确诊病例数和日累计死亡病例数进行预测，以期进一步掌握新冠肺炎疫情发展规律，为政府防控新冠疫情提供参考。

1 研究方法

图1 BP神经网络模型Fig.1 BP neural network model

1.1 BP神经网络

BP 神经网络是将误差进行反向传播训练的多层前馈神经网络，如图1 所示，其由输入层、隐藏层和输出层构成。BP 神经网络的学习过程由信号正向传播和误差反向传播组成。正向传播过程中，输入参数由输入层传递到隐藏层，经由隐藏层处理，传向输出层。若输出层的实际输出值达不到期望值，则进行误差信号反向传播。误差反向传播是将输出误差以某种形式由隐藏层向输入层传播，并沿途调整各层间的权值与阈值，使误差沿梯度下降。通过反复上述过程，直到输出误差降低到可接受的程度或达到设定的训练次数为止，其流程如图2。

1.2 时间序列神经网络

时间序列预测是指按照一定的时间顺序，对历史数据进行整理和分析，找到符合数据变化规律的函数，根据该函数预测下一阶段的数据，掌握事物的未来发展趋势。各种事物发展变化是非线性的，同时受多种因素变化影响，因此很难找到描述事物发展变化规律的函数。神经网络具有高强度的自我学习能力，能以任何精度逼近非线性函数，为寻找事物发展规律提供了有效的解决办法。

2 时间序列神经网络预测模型的建立

图2 BP神经网络流程图Fig.2 Flow chart of BP neural network

采用MATLAB 编程建立、训练、测试时间序列神经网络模型，分析不同结构参数网络模型的性能，选择合理的网络结构，实现对历史数据的学习与训练。

2.1 时间序列模型

设有一时间序列X(i)，i=1，2，…，N，其中N为观测点个数，则该时间序列模型可描述为

式中：F[]∙为非线性作用函数；t为模型的阶数。

建立时间序列模型是为寻找函数，若网络中间层神经元的特性函数具有任意阶导数，中间层可根据需要任意设置神经元个数，则3层BP网络模型可任意精度逼近任何连续函数。因此，只要选取合理的神经网络结构参数，使用神经网络即可精确地反演出复杂的非线性函数。

2.2 时间序列神经网络模型

2.2.1 样本集的生成

对于时间序列神经网络预测通常是根据已有的样本数据建模并对其进行训练，就单个时间序列X(i)，i=1，2，3，…，N，假定用前t个点数据预测第t+1个点数据，该模型输入向量是前t个点，则输出向量是第t+1个点的数值。对于时间序列X(i),i=1，2，3，…，N，则可生成N-t个样本，如表1。

表1 时间序列神经网络样本的构造方法Tab.1 Construction method of time series neural network samples

根据表1所示的时间序列神经网络构造方法，文中设置输入节点数为3，即用前3个监测数据预测下一位数据，则输出节点数为1。为提高模型预测的精确度，需对模型的输入向量和输出向量进行数据预处理。将数据处理在[0，1]范围能减小每个样本数据之间较大的误差，此处采用最大最小归一化法，如

式中：X为输入变量；X，X为输入变量中的最大值和最小值；X′为归一化后的输出变量。

2.2.2 神经网络结构参数的设置

隐含层节点数影响神经网络预测模型的精度，节点过多会出现过度拟合现象，节点过少会导致模型不准确。根据相关经验公式，使用试凑法确定隐含层的节点数；根据样本训练不同隐含层节点时造成的误差结果，选取最小误差时对应的隐含层数；建立时间序列神经网络模型，其公式如下

式中：l为隐含层的节点数；m和p分别为输入层、输出层的节点数；a为1到10之间的调整常数。

通过试凑法可知，隐含层节点数在3～12之间，当选取隐含层节点数7时，样本的模型误差最小。因此当输入层的节点数为3个、输出节点数为1个、隐含层节点数为7个时，模型的预测效果较好。对于隐含层神经元的传输函数采用S型正切函数tansig，输出层神经元的传输函数选取purelin函数，取误差指标10，设置最大训练循环次数为1 000。

2.2.3 模型评价指标的选取

采用平均绝对误差(E)和均方根误差(E)为模型预测性能评价指标，评价时间序列神经网络预测模型的预测效果，两种指标定义式如下：

式中：n 为预测次数；ŷ，y分别为第i个样本的预测值和实际值。

3 结果分析

3.1 数据集

数据来源于国家卫生健康委员会官网提供的每日疫情通报(http://www.nhc.gov.cn/xcs/yqtb/list_gzbd.shtml)，北京市卫生健康委员会官网提供的每日疫情通报(http://wjw.beijing.gov.cn/wjwh/ztzl/xxgzbd/gzbdyqtb/index.html)，武汉市卫生健康委员会官网提供的每日疫情通报(http://wjw.wuhan.gov.cn/gsgg/index.shtml)。

3.2 时间序列神经网络预测模型的验证

为验证时间序列神经网络预测模型的有效性，以武汉市2020年1月20日到2020年3月17日的新冠肺炎现存累计确诊病例数为数据来源，以2020年2月26日之前的数据为训练数据，采用时间序列神经网络预测模型预测2020年2月27—29日3 d的现存累计确诊病例数，将其与文献[22]中多项式函数模型、指数函数模型、双曲函数模型、幂函数模型、支持向量机非线性组合动态传播率模型和BP神经网络模型6种预测模型现存累计确诊病例数的预测值和实际值进行对比，结果如表2。

表2 不同预测模型的现存累计确诊病例数的预测值Tab.2 Prediction value of existing cumulative number of confirmed cases of different predictive models

由表2 可知，相较于其他6 种模型，时间序列神经网络模型预测的现存累计确诊病例数更接近实际值。为直观检验各模型的预测精度，将各模型的预测值与实际值据代入式(4)，(5)，得到各模型的平均绝对误差(E)和均方根误差(E)，结果如表3。由表3可看出：相对于其他6个预测模型，时间序列神经网络模型预测现存累计确诊病例数的E和E最小，分别为36.27和80.03；BP神经网络模型的E和E分别为167.55，322.73；支持向量机非线性组合动态传播率模型的E和E分别为137.25，349.09；其他模型的E和E均高于以上3种预测模型。由此表明，时间序列神经网络模型的预测精度最高，BP神经网络模型和支持向量机非线性组合动态传播率模型的预测精度相差不大，两者预测精度次之。

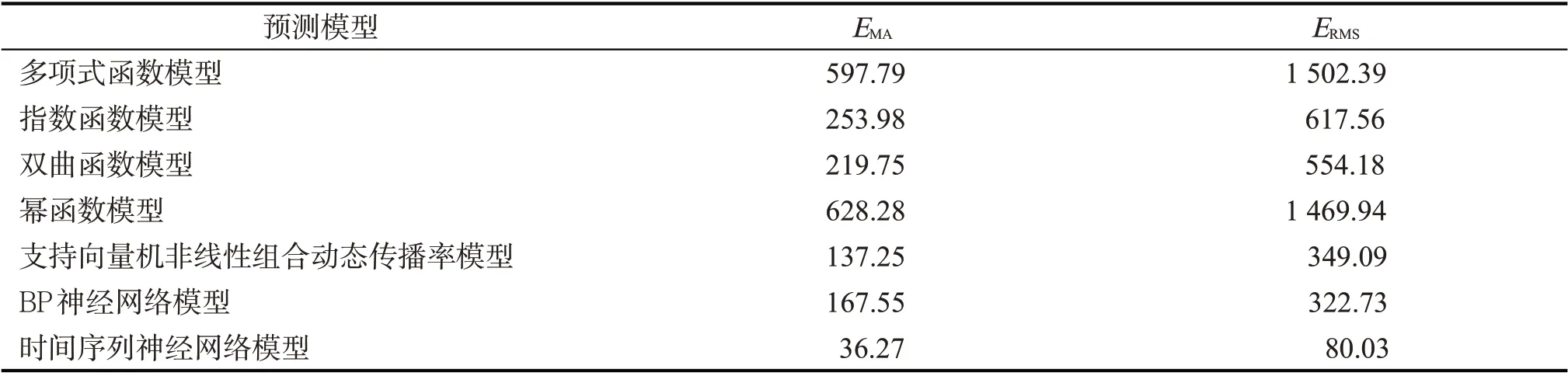
表3 不同预测模型的平均绝对误差和均方根误差Tab.3 Mean absolute error and root mean square error of different predictive models

3.3 时间序列神经网络预测模型的预测结果分析

利用时间序列神经网络预测模型对2020年2月12日—2020年4月15日全国、武汉市和北京市的新冠病毒肺炎日累计确诊病例数和日累计死亡病例进行预测，并分别对全国、湖北省武汉市和北京市的日累计确诊病例数和日累计死亡病例数的相对误差进行分析，结果如图3，4。预测初始点为2020年2月12日，以该点为图3，4的时间轴原点。

图3 日累计确诊病例数与相对误差的仿真结果Fig.3 Simulation results of daily cumulative number of confirmed cases and relative error

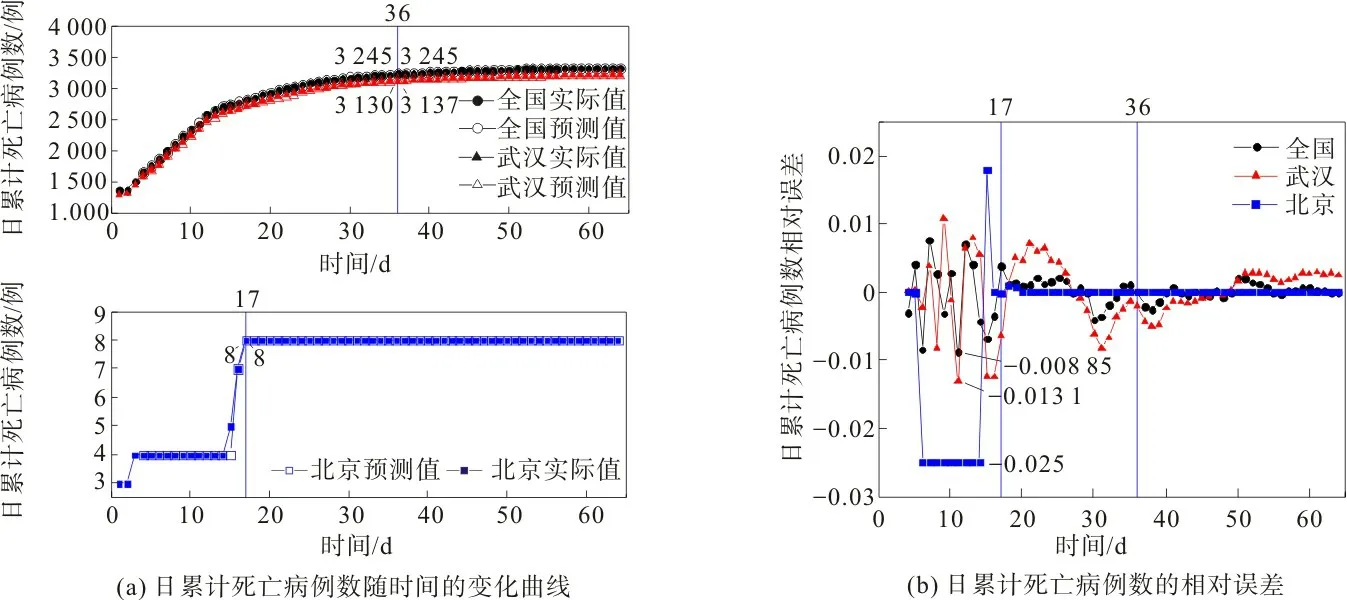
图4 日累计死亡病例数与相对误差的仿真结果Fig.4 Simulation results of daily cumulative number of death cases and relative error

由图3(a)可知：3月6日后全国、武汉市和北京市的日累计确诊病例数逐渐趋于平稳，日累计确诊病例数分别为80 651，67 666，415例；3月6日全国的日累计确诊病例数实际值和预测值分别为80 651，80 598例，武汉市的日累计确诊病例数实际值和预测值分别为67 666，67 630例，北京市的日累计确诊病例数实际值和预测值分别为415，415例，预测值与实际值十分接近。由图3(b)可知：时间序列神经网络预测模型的预测值和实际值的相对误差较小，绝对值基本上小于2.0%，全国、武汉市和北京市的日累计确诊病例数的最大相对误差分别为0.47%，-0.57%和-1.96%；时间序列神经网络预测模型的相对误差在3月6日前波动较大，3月6日后波动较小，这与日累计确诊病例数的变化相一致。日累计确诊病例数与相对误差的仿真结果表明时间序列神经网络预测模型准确性高。

由图4(a)可知：3月18日后全国和武汉市的日累计死亡病例数逐渐趋于平稳，日累计确诊病例数分别为3 245，3 130例；2月28日后北京市的日累计死亡病例数逐渐趋于平稳，日累计死亡病例数为8例；3月18日全国日累计死亡病例数实际值和预测值均为3 245 例，武汉市的日累计死亡病例数实际值和预测值分别为3 130，3 137例；2月28日北京市的日累计死亡病例数实际值和预测值均为8例。由图4(b)可知：时间序列神经网络预测模型的预测值和实际值的相对误差较小，绝对值基本上小于2.5%，全国、武汉市和北京市的日累计死亡病例数的最大相对误差分别为-0.89%，-1.31%和-2.50%；全国和武汉市的时间序列神经网络预测模型的相对误差在3月18日前波动较大，3月18日后波动较小，北京市的时间序列神经网络预测模型的相对误差在2月28日前波动较大，2月28日后波动较小，这与其日累计死亡病例数的变化相一致。日累计死亡病例数与相对误差仿真结果表明时间序列神经网络预测模型准确性高。

为进一步检验模型的精确性，将全国、武汉市和北京市的时间序列神经网络预测模型的最后5个预测数据和实际监测数据进行对比，结果如表4。从表4可看出，时间序列神经网络预测模型的日累计确诊病例数和日累计死亡病例数的预测值与实际值均很接近，表明时间序列神经网络预测模型准确性高。

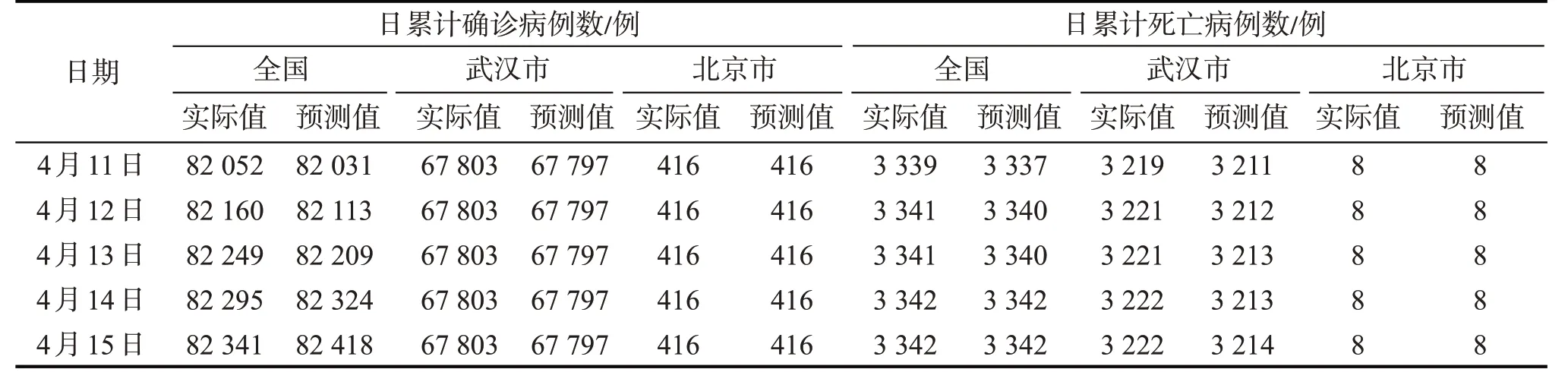
表4 测试结果与实际值对比Tab.4 Comparison between test results and actual values

4 结论

使用MATLAB 软件对历史数据进行学习与训练，建立新冠肺炎病例时间序列神经网络预测模型，对2020年1月20日到2020年3月17日武汉市现存累计确诊病例数进行预测，将其预测结果与其他6种预测模型进行比较，验证模型的有效性；利用建立的时间序列神经网络预测模型对2020年2月12日至4月15日全国、武汉市和北京市日累计确诊病例数和日累计死亡病例数进行预测，得到以下主要结论：

1)与多项式函数模型、指数函数模型、双曲函数模型、幂函数模型、支持向量机非线性组合动态传播率模型和BP神经网络模型等6种预测模型相比，采用时间序列神经网络预测模型预测的现存累计确诊病例数更接近实际值，其平均绝对误差和均方根误差最小，预测精度最高。

2)采用时间序列神经网络预测模型对全国、武汉市和北京市日累计确诊病例数和日累计死亡病例数的预测结果表明：日累计确诊病例数和日累计死亡病例数随时间变化逐渐趋于平稳，预测值与实际值接近；日累计确诊病例数和日累计死亡病例数最大相对误差绝对值分别为2.0%和2.5%，时间序列神经网络预测模型准确性高。