LCL型并网逆变器大小信号模型比较与分析

李建文， 李戎， 吴滨源， 孙伟

(1.华北电力大学 新能源电力系统国家重点实验室，河北 保定 071003；2.国网河北省电力有限公司保定供电分公司，河北 保定 071000)

0 引 言

能源枯竭，环境危机，光伏分布式发电系统发展迅猛，逆变电路中采用脉宽调制(pulse width modulation, PWM)控制不可避免的带来了丰富的开关谐波，需选取合适的滤波器，LCL型滤波器凭借体积小、成本低的优点逐渐成为并网逆变器电路的应用首选[1-3]，但其频率响应存在谐振尖峰，威胁到并网电流质量及系统稳定性[4-5]。围绕着并网逆变器带来的系统稳定性问题国内外已展开了丰富的研究，建模过程作为分析问题的第一步关乎到结论的正确与否，因而模型的正确性和精度就显得尤为重要。理想模型应兼顾正确性和复杂度，使其既能正确反映电路性能且具有高的精度，又不至过于复杂，利于实际工程应用[6]。目前的论文研究在建模上大体可分为大信号模型与小信号模型两种。

大信号模型通过对开关器件在一个运行周期内取平均得到，其在整个定义的范围内有效；小信号模型围绕着某一特定工作点使用泰勒级数展开得到，获得的线性模型只在特定工作点微小变化范围内有效[7-8]。并网逆变器系统利用小信号建模考虑的因素更加全面：锁相环(phase-locked-loop，PLL)作为典型的反馈控制电路能够实现对频率的快速跟随[9]，但在交流源电压受扰动后会输出角Δθ，使得系统坐标系与控制坐标系不再重合，为提高系统稳定性文献[10-15]从不同方面展开研究，文献[15]指出PLL带宽会影响系统稳定性，进而利用相角补偿的方法增加系统的相位裕度，解决PLL带宽过高引起的系统稳定性问题。

现有文献围绕着对LCL型并网逆变器参数的整定、通过不同方法提高系统稳定性及加入反馈控制后提高模型的准确性和控制性能的一致性已展开了丰富的研究，这其中既有利用大信号模型分析方法[16-19]也有利用小信号模型[20-22]分析方法，本文着重分析两种模型各自适用性。分别在大、小信号模型下对并网逆变器系统建模，在电路拓扑中加入并网电流和电容电流反馈控制环节，小信号模型在此基础上再加入PLL控制环节。改变参数探究对系统稳定性的影响，通过建模过程和得出的结论比较二者异同，总结各自适用性，讨论多逆变器并网时，通过牺牲模型的精确度、简化控制系统的设计、降低模型阶数而采用大信号模型是否可取。最后在MATLAB/Simulink中搭建实际并网模型，验证模型分析稳定性得到的结论及大信号模型在多逆变器并网时的适用性。

1 典型控制下LCL型并网逆变器大、小信号模型

1.1 大信号模型

分布式电源经逆变电路将直流转换成三相交流电，通过LCL型滤波器抑制并网电流中的开关谐波，将电能馈送至用户及系统中。图1给出了LCL型并网逆变器的电路拓扑。

图1 LCL型并网逆变器拓扑结构Fig.1 Topology of LCL-filter-based grid-connected inverter

LCL型并网逆变器由逆变侧电感L1、逆变侧电阻RL1、滤波电容C1、滤波电容寄生电阻RC1、网侧电感L2和网侧电阻RL2构成。Vdc为直流侧电压，ug为电网电压，uPCC为公共耦合点处电压，uC为滤波电容电压，uinv为逆变器输出电压。iL1、iC1和ig分别为逆变侧电感电流、滤波电容电流和并网电流。

逆变器输出端为时变交流量，利用大信号模型建模时为简化控制系统设计，便于调节并网逆变器的有功和无功功率，并在应用PI调节器对并网电流基波分量调节时不产生静态误差，通过坐标变换将abc坐标系下的变量转移至d-q坐标系下。由此产生的模型可视作是一双输入双输出(MIMO)系统，所得传递函数为2×2的矩阵，其副对角线上的元素代表d-q轴间的交叉耦合项。

为抑制LCL型并网逆变器的谐振尖峰，控制侧选取基于电容电流反馈的有源阻尼法，并利用PI控制实现负载和电网电流参考值的快速跟随，其控制框图如图2所示[19]。

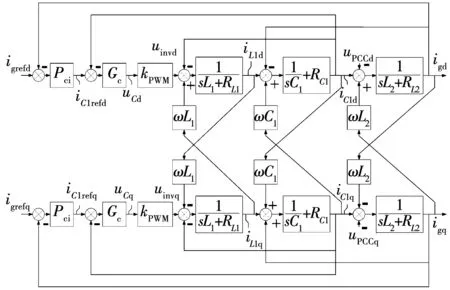
图2 典型控制环节下LCL型逆变器传递函数Fig.2 Circuit transfer function of LCL-filter-based grid-connected inverter under typical control

其中，Pci为PI控制器，Gc为电容电流反馈比例控制器，kPWM为逆变器PWM调制等效增益，取kPWM=1。

将公共耦合点电压作为输入，并网电流作为输出，所得传递矩阵包含d-q轴的自导纳和交叉耦合导纳，即

(1)

化简传递流程图，得到大信号模型下逆变器的输出导纳表达式为

(2)

式中：E为单位矩阵；Gc=diag(kc,kc)，kc为比例系数；Pci=diag(Gi,Gi)，Gi=kpi+kii/s。

1.2 小信号模型

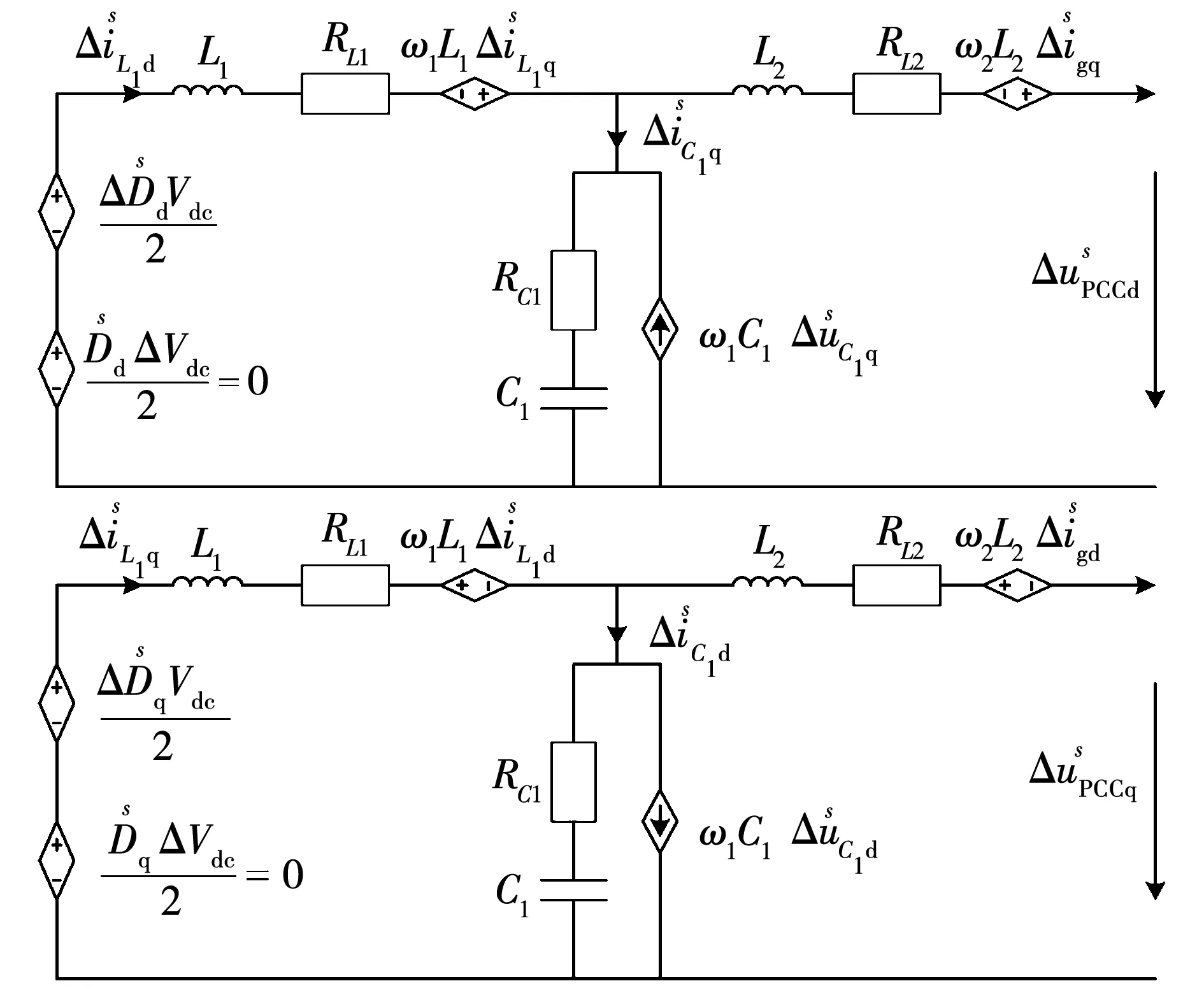
图3 d-q坐标系下小信号电路模型Fig.3 Small-signal modeling under d-q coordinate system

闭环控制中加入PLL环节，其具有监测系统频率与实现相位快速跟随的功能使得所建模型更为精确。根据图3得到的传递函数由于d-q轴间存在耦合，形式相对复杂，化简得到考虑PLL的控制环节的传递函数如图4所示[15]。

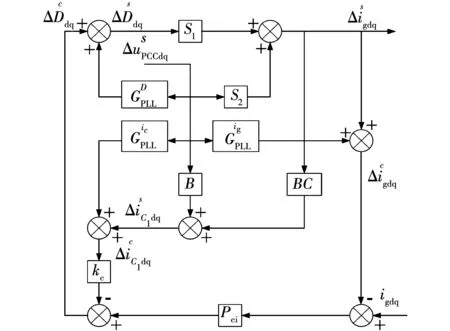
图4 LCL型逆变器小信号模型Fig.4 Small-signal modeling of LCL-filter-based grid-connected inverter

同样将公共耦合点电压作为输入，并网电流作为输出，化简传递函数框图得到逆变器输出导纳为

(3)

2 大、小信号模型适用性分析

2.1 两种模型分析参数变化对系统稳定性的影响

2.1.1 大信号模型

根据式(2)得到逆变器输出导纳Yout_da的Bode图，定性分析LCL参数、有源阻尼系数及电流调节器参数对逆变器输出导纳Yout_da的影响，结论归纳见表1。

表1 大信号模型分析参数变化对系统稳定性影响的结果

2.1.2 小信号模型

定义电网阻抗Zg与LCL型并网逆变器输出导纳Yout_xiao的乘积为回率矩阵L，根据L的特征函数曲线判断系统稳定性[15]，研究和单位圆相交截止频率fc下的相角裕度，求取系统的稳定范围和裕度。结论归纳见表2。

观察表1和表2发现，大、小信号模型在分析参数变化对系统稳定性影响时得到的结论具有一致性：应用小信号模型分析逆变器侧电感L1时认为其参数变化对系统稳定性影响很小，与大信号模型分析结果相吻合；滤波电容C1、网侧电感L2参数增大使得系统趋于不稳定，与大信号模型分析结果相吻合；有源阻尼系数kc增大，Nyquist曲线向内收缩，相角裕度增大，表明系统愈加稳定，与大信号模型分析结果相吻合。

表2 小信号模型分析参数变化对系统稳定性影响的结果

2.2 两种模型特性比较

为更直观的挖掘二者适用性，表3给出一组并网逆变器参数。

表3 并网逆变器参数

根据式(2)和式(3)，绘制两种模型下输出导纳Yout的Bode图，如图5所示。

观察图5发现，大信号模型在低频段内Ydd、Ydq、Yqd和Yqq呈负导纳，小信号模型在低频段内幅值增益约等于1，证明小信号模型较大信号模型在低频域具有更好的跟踪效果；高频段内由于LCL型逆变器的特性，二者在4.1 kHz均出现一谐振尖峰，大信号模型在此处幅值较小，小信号模型对谐振点反应敏感，幅值较高；电网工频50 Hz处小信号模型会出现尖峰，大信号模型未出现。

2.3 适用性分析

2.1节运用两种模型在分析参数变化对系统稳定性影响时得出的结论是一致的。但应该指出，大信号模型未考虑电力电子器件非线性特性、PLL环节使得模型更为简单，输出导纳阶数较低。小信号模型考虑电力电子器件在PWM控制下的线性运行点、加入PLL比例积分环节使得阶数较高，总结两种模型的异同如表4所示。

表4 大小信号模型的比较

当前光伏装机容量连年上升，其在电网渗透率越来越高，配电网中多逆变器并网已是一种趋势，然而逆变器间的交互常引发谐振失稳，需进一步对系统建模找到谐振点并加以治理[23-24]，考虑到实际工况中不同厂家生产的并网逆变器参数不尽相同，且小信号模型下输出导纳表达式(3)较大信号模型式(2)高出3阶，在分析多逆变器并网系统时若继续采用小信号模型势必会增加分析工作量、增大建模难度。而此时模型的精确度已是次要考量因素，即相较于逆变器内部参数变化对系统稳定性的影响，更关注逆变器之间和逆变器与电网阻抗间交互影响造成的系统不稳定的点。大信号模型凭借简化控制系统设计，更易推导得出传递函数表达式，为进一步分析系统谐振点提供了便利。

图6给出两种模型下相同参数的两台逆变器并联后系统输出导纳YoutBode图，对比发现二者均在3.75 kHz处出现谐振尖峰，证明了在分析多逆变器并网时采用大信号模型可以有效确定并网系统的谐振点。

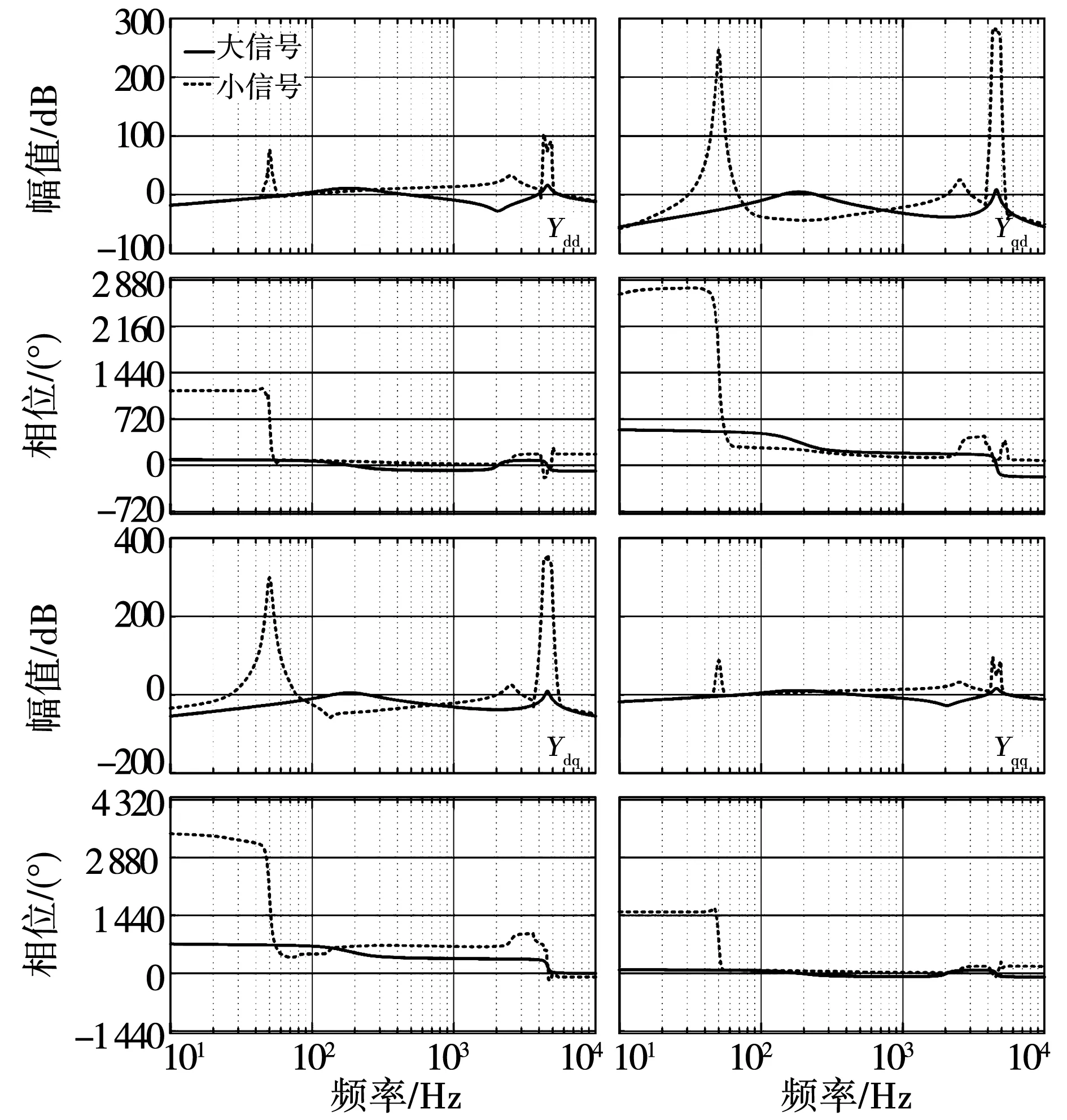
图6 两个逆变器并网时两种模型输出导纳Yout对比图Fig.6 Comparison diagram of output admittance Yout between the two model when two inverters are connected to the grid

3 仿真验证

第2节中分别在大、小信号模型下讨论了LCL型滤波器参数及控制参数变化对系统稳定性的影响，进而就一台逆变器并网系统及两台逆变器并网系统给出了应用大、小信号模型输出导纳对比图。为了验证理论分析的正确性，在MATLAB/Simulink中搭建系统具体模型，并网逆变器参数见表3，图7(a)给出了此时并网电流波形及FFT分析。

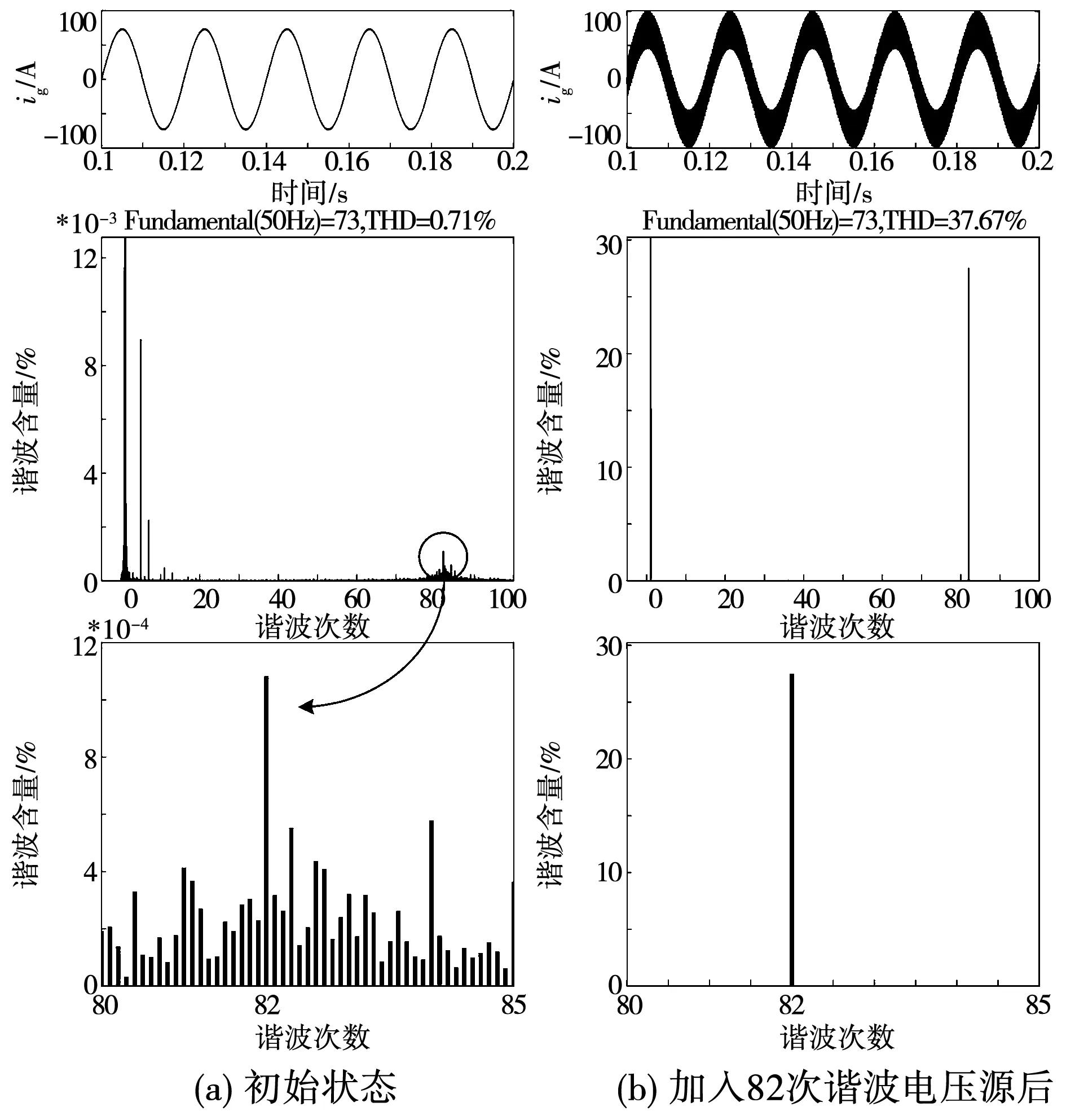
图7 典型参数下并网电流波形及FFT分析Fig.7 Grid-connected current waveform and Fourier analysis result under typical parameters

观察图7(a)发现，并网逆变器系统存在82次谐波，图5给出的两种模型下输出导纳对比图均在4.1 kHz处出现谐振尖峰，与其结果相吻合。现在控制回路加入谐波电压源，幅值为并网点电压额定值的5%，频率为4.1 kHz。加入背景谐波后并网电流波形及FFT分析如图7(b)所示。

观察图7(b)发现，除基波电流外，在谐振点4.1 kHz(82 pu) 处电流被明显放大，并网电流波形产生严重畸变，已不满足并网要求。验证了2.2节应用大、小信号模型输出导纳Bode图确定并网系统谐振点的有效性。

3.1 参数变化对系统稳定性的影响

改变滤波器参数、有源阻尼系数及PLL参数，观察并网电流波形，验证各项参数对系统稳定性的影响与实验结果是否一致。

1)改变滤波电容参数。

分别减小、增大滤波电容参数，取C1=7.5、12.0 μF，观察并网电流波形及FFT分析，并在控制回路加入谐波电压源，幅值为并网点电压额定值的5%，频率为相应参数下并网逆变器系统谐振频率，对比不同参数下并网电流波形畸变程度及谐波放大程度，得到图7～图9。

图8 滤波电容C1=8 μF时并网电流波形及FFT分析Fig.8 Grid-connected current waveform and Fourier analysis result when filter capacitor C1=8 μF

图9 滤波电容C1=12 μF时并网电流波形及FFT分析Fig.9 Grid-connected current waveform and Fourier analysis result when filter capacitor C1=12 μF

观察图7～图9发现，随着滤波电容C1增大，谐波含量基本未变，谐振峰值向低频方向移动，控制回路加入谐波源后谐振峰值均得到有效放大，且放大程度及谐波含量接近，与2.1节应用大、小信号模型得到的结论相吻合。

2)改变有源阻尼系数。

分别减小、增大有源阻尼系数，取kc=0.8、1.5，观察并网电流波形及FFT分析，并在控制回路加入谐波电压源，幅值为并网点电压额定值的5%，频率为相应参数下并网逆变器系统谐振频率，对比不同参数下并网电流波形畸变程度及谐波放大程度，得到图7、图10和图11。

图10 有源阻尼系数kc=0.8时并网电流波形及FFT分析Fig.10 Grid-connected current waveform and Fourier analysis result when active damping coefficient kc=0.8

观察图7、图10和图11发现，随着有源阻尼系数kc增大，谐波含量逐渐减少，谐振峰值未变，控制回路加入谐波源后谐振峰值均得到有效放大，但放大程度及谐波含量逐渐降低，与2.1节大小信号模型得出的结论相吻合。

图11 有源阻尼系数kc=1.5时并网电流波形及FFT分析Fig.11 Grid-connected current waveform and Fourier analysis result when active damping coefficient kc=1.5

3)增大PLL参数，观察并网电流波形及FFT分析，得到图12。

观察图12发现，PLL带宽增大后谐波含量增加；更重要的是，电流大幅偏离额定电流igref，与2.1节应用小信号模型得到的结论相吻合。但请注意，一定范围内增大PLL系数系统并网电流并未振荡失稳，只是其电流幅值大幅偏离额定值。

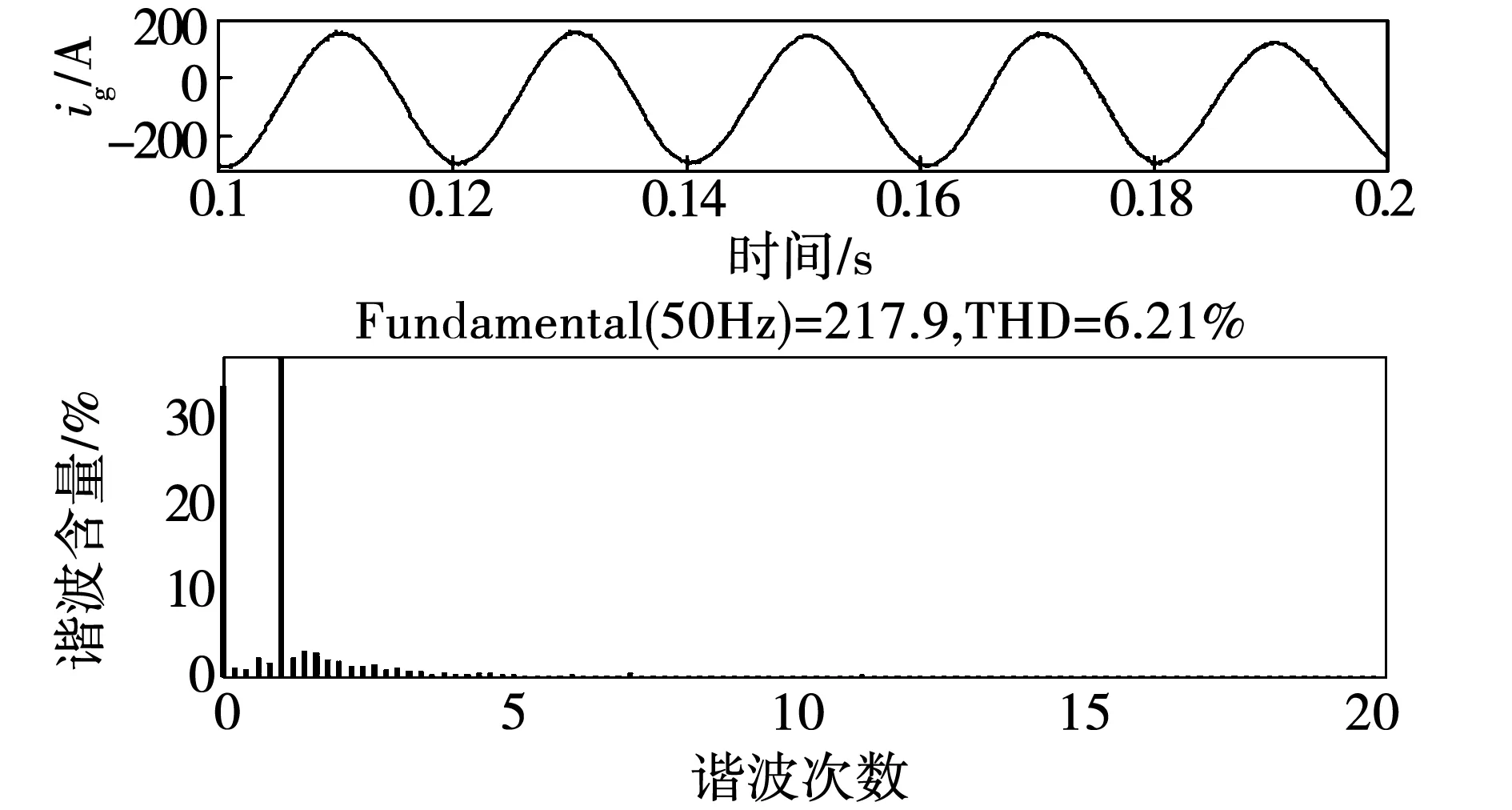
图12 增大PLL参数后的并网电流波形及FFT分析Fig.12 Grid-connected current waveform and Fourier analysis result after increasing PLL parameters

3.2 多逆变器并网谐振失稳验证

图6给出的2个逆变器并网时输出导纳对比图均在3.75 kHz处出现谐振尖峰，现搭建2个相同参数的LCL型逆变器，并在控制回路加入谐波电压源，幅值为并网点电压额定值的5%，频率为3.75 kHz，观察并网电流波形及FFT分析如图13所示。

观察图13发现，并网逆变器系统存在75次谐波，与图6给出的结果相吻合。控制回路加入谐波源后谐振峰值得到有效放大并网电流波形产生严重畸变，已不满足并网要求。验证了2.3节应用大、小信号模型输出导纳Bode图确定多逆变器并网系统谐振点的有效性。

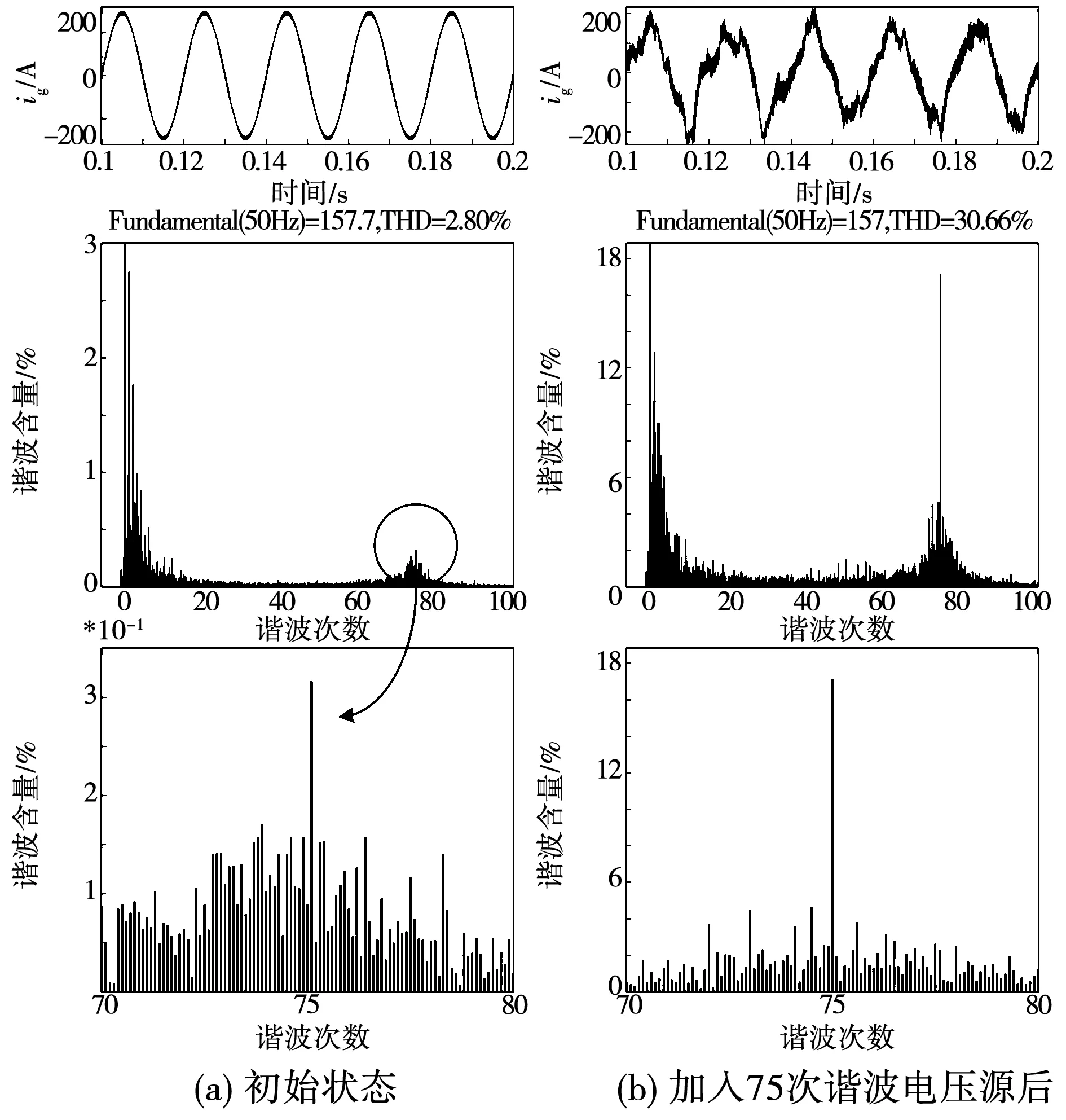
图13 两台相同参数的LCL型逆变器并网后的电流波形及FFT分析Fig.13 Grid-connected current waveform and Fourier analysis result after connecting two LCL-filter-based grid-connected inverter with same parameters in parallel

4 应用拓展

弱电网背景下，并网逆变器控制侧取滤波电容电压进行跟踪实现对有功、无功的控制被证明较传统电流型控制具有更好的运行特性，稳定程度更高[25]。现给出这一电压型控制逆变器的控制框图，应用大信号模型确定其并网谐振点。

电压型控制逆变器控制框图如图14所示，采用电压电流双闭环控制方式，电压外环给定值由功率给定环节计算得到，电流内环为逆变器侧电感电流iL1反馈的有源阻尼控制。由于功率环时间常数远大于电压环时间常数，因此可认为电压环电压参考信号恒定。图14中：U*(s)为电压参考信号；Gu(s)和Gi(s)分别为电压环PI调节器和电流环PI调节器传递函数；Lg为电网等效电感。设置参数如表5所示。

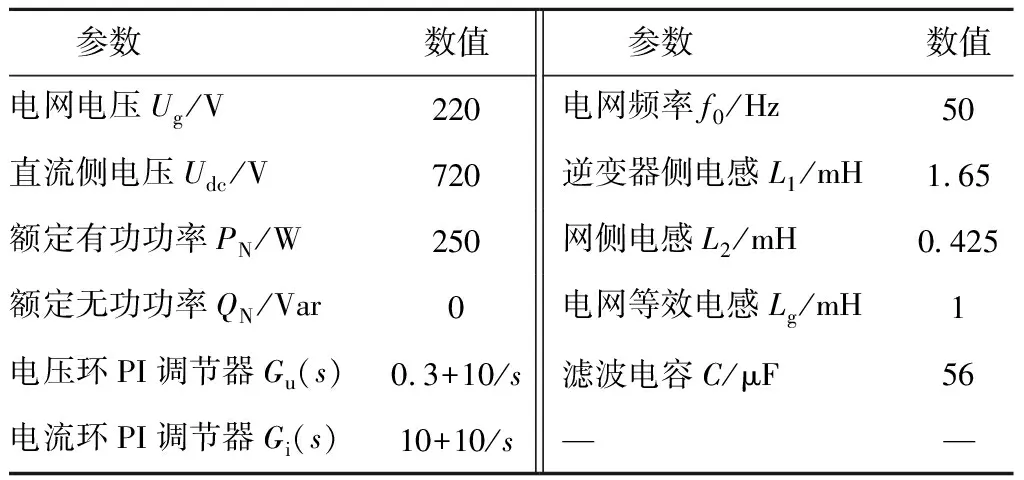
表5 电压型控制逆变器并网参数设置

根据图14对电压型控制逆变器进行戴维南等效，如图15所示，其中，Us和Zo1分别为电压型控制逆变器的等效电压源和等效输出阻抗，ZL2=sL2，Zg=sLg。

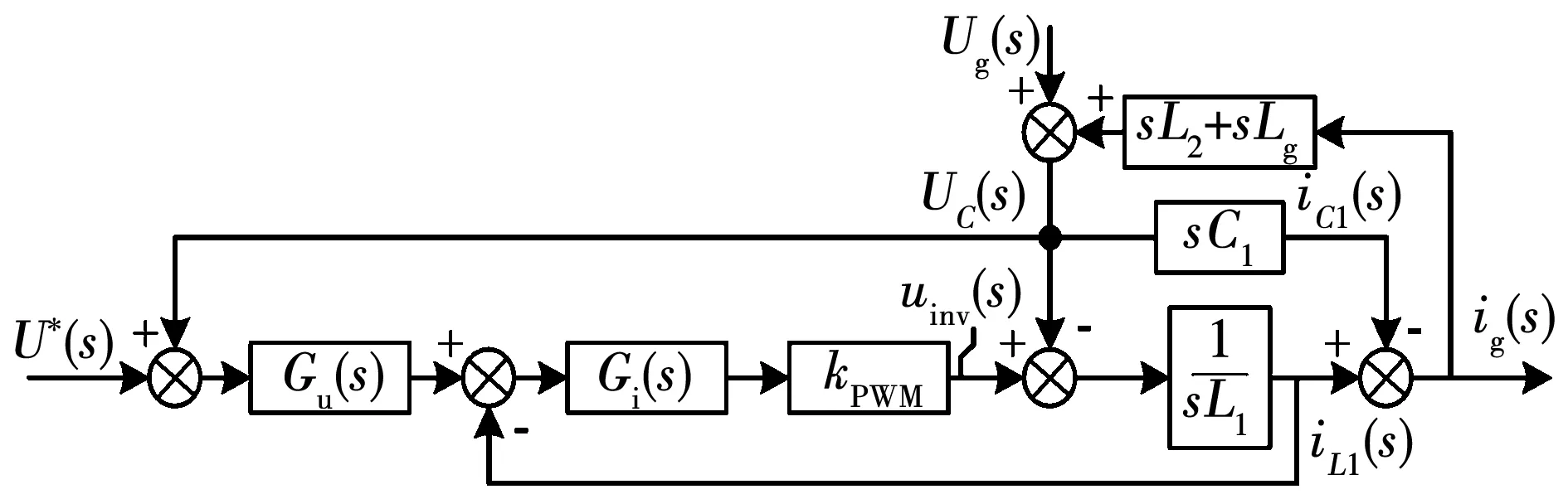
图14 电压型控制逆变器控制框图Fig.14 Control block diagram of voltage-controlled inverter

图15 电压型控制逆变器戴维南等效电路Fig.15 Thevenin equivalent circuit of voltage-controlled inverter

结合图14和图15推导得到Us和Zo1的表达式分别为：

G1U*;

(4)

(5)

由图15推导得出电压型控制逆变器并网电流的表达式为

ig(s)=Φ1(s)U*-Φg(s)Ug。

(6)

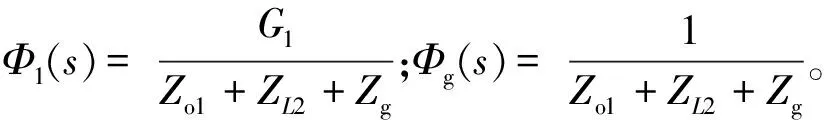
由式(6)可知，并网电流ig(s)由两部分组成，其中：Φ1(s)表示逆变器自身对ig(s)产生的影响；Φg(s)表示逆变器与电网交互对ig(s)产生的影响。根据式(6)绘制电压型控制逆变器并网电流ig(s)的Bode图如图16所示。

图16 电压型控制逆变器并网电流ig(s)Bode图Fig.16 Bode diagram of voltage-controlled inverter grid-connected current ig(s)

观察图16发现，电压型控制逆变器在244 Hz处存在谐振尖峰，为验证应用大信号模型确定的这一谐振点，在MATLAB/Simulink中搭建实际并网模型，并在控制回路加入5次谐波电压源，幅值为并网点电压额定值的5%，观察并网电流波形及FFT分析如图17所示。

图17 电压型控制逆变器并网电流波形及FFT分析Fig.17 Grid-connected current waveform and Fourier analysis of voltage-controlled inverter

观察图17 (a)和(b)发现，控制回路加入5次谐波电压源后谐波含量大大增加，且5次谐波被放大，波形畸变明显，已不满足并网电流标准，验证利用大信号模型确定不同控制类型逆变器并网谐振点的有效性。

5 结 论

对LCL型并网逆变器在大、小信号下建模，分析参数变化对系统稳定性影响，进而比较两种模型异同，分析其适用性，得到如下结论：

1)两种模型在分析参数变化对系统稳定性影响时得出的结论具有一致性：逆变侧电感参数对系统稳定性影响不大。滤波电容增大，谐振频率降低，截止频率下相角裕度减小，系统趋于不稳定。网侧电感增大，谐振频率降低，谐振幅值降低，系统稳定性降低。有源阻尼系数增大，系统稳定性得到改善。电网阻抗愈大，系统稳定性变差。小信号模型下加入PLL控制环节，增大PLL带宽，系统稳定性变差。

2)二者建模难度，模型精确度不同。小信号模型考虑电力电子器件在PWM控制下的线性运行点、PLL的动态控制环节，使得模型更精确的同时也更复杂，体现在小信号模型在低频域内跟踪效果更好，对谐振频率更敏感，同时输出导纳阶数更高。

3)二者适用性不同。分析单逆变器并网系统稳定性时采用小信号模型考虑因素更全面，模型精确度更高，而在新能源发电系统渗透率越来越高的今天，应对用电负荷变化随时需要灵活控制并网台数，多逆变器之间及逆变器与电网阻抗间均存在交互影响，有必要对系统建模并分析其频率响应特性，找到不稳定点，在不改变原有电路拓扑的基础上改进控制算法对谐振尖峰加以治理。考虑到各个逆变器的参数不尽相同，若采用小信号模型会增加建模难度，模型阶数的升高意味着其结构也更为复杂，而应用大信号模型能够简化控制系统设计，找到系统谐振点并加以治理，以满足并网要求。

本文着重对两种模型各自的特性及适用性进行论述，下一步可针对多逆变器并网带来的系统稳定性问题展开研究，以此证明在对高阶复杂系统建模时应用大信号模型确定系统谐波谐振点的有效性。