一种120°坐标系下的快速SVPWM过调制算法

王健， 章玮

(浙江大学 电气工程学院，杭州 310027)

0 引 言

空间矢量脉宽调制(space vector pulse width modulation，SVPWM)具有电压利用率高、开关谐波含量低且易于数字实现等优点，被广泛应用于交流电机调速领域[1-2]。通过过调制技术可以进一步提高直流母线电压利用率，进而提高电机的转速和输出转矩，增强电机运行性能[3]。

比较主流的双模式过调制算法由Holtz最早提出，该算法将过调制区域分为过调制I区和过调制II区并在不同区域采用不同改进策略[4]。文献[5]就最小相位误差、最小幅值误差和最小分量误差3种典型改进策略进行了比较分析，提出了一种电压谐波含量最小的线性化过调制方法，然而分段的处理使得算法变得更加复杂。文献[6-7]针对无电解电容永磁同步电机驱动系统改进了双模式过调制算法，减小了电压和电流的畸变。对于非典型拓扑结构下过调制算法的研究也是一个热门方向，如发生缺相故障[8]或者多电平逆变器的过调制算法[9-10]。

相较于传统的SVPWM算法，文献[11-12]提出了一种基于120°坐标系的快速SVPWM算法，明显地减少了计算量。文献[13]在此基础上提出一种分段非线性拟合的过调制算法，对文献中调整后的参考电压矢量进行非线性拟合，减少了计算量但有一定精度误差。文献[14]提出了120°坐标系下最小幅值误差过调制算法，调整后的参考电压矢量的幅值与调整前相差最小，计算简单且易于实现但谐波含量较高且非线性关系明显。

针对以上问题，本文引入120°坐标系SVPWM算法，根据最小相位误差原理利用三相上桥臂开通时间判断调整参考电压矢量的幅值和相位，并推导120°坐标系下的算法表达式，统一整个调制区域的计算流程，大大减少过调制算法的计算时间，同时具有优秀的谐波抑制效果。最后，通过实验对本文所提算法进行验证。

1 120°坐标系SVPWM算法

在三相逆变器中，三相的输出电压波形分别对应三相桥臂的开关状态，因此可以直接利用三相桥臂的开关状态合成参考电压矢量[10-11]。图1是参考电压矢量合成示意图，Ua、Ub和Uc为三相桥臂电压矢量，空间上互差120°，Uref为参考电压矢量。

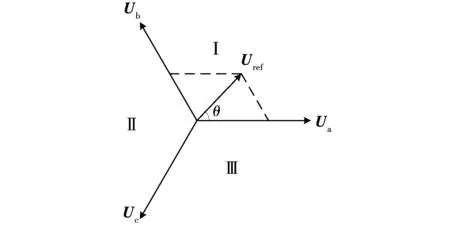
图1 120°坐标系矢量合成示意图Fig.1 Schematic diagram of 120° coordinate system vector synthesis

对于图1中的参考电压矢量Uref，根据伏秒平衡原理，有

TsUref=TaUa+TbUb+TcUc。

(1)

其中：Ts为三相桥臂开关周期；Ta、Tb和Tc为三相电压的作用时间。选取Ua和Ub构建120°坐标系，将Uc分解到Ua和Ub轴上，代入得

TsUref=(Ta-Tc)Ua+(Tb-Tc)Ub。

(2)

令Tx=(Ta-Tc)、Ty=(Tb-Tc)，式(2)可以表示为

TsUref=TxUa+TyUb。

(3)

根据正弦定理解式(3)得：

(4)

其中：Udc为直流母线电压；Uref为矢量Uref的幅值；Ua和Ub为矢量Ua和Ub的幅值，Uα和Uβ为Uref在α-β坐标系上分量的幅值。

令Ta、Tb、Tc中最小的一个为0，可得

[TaTbTc]=

(5)

由此得到了三相电压的作用时间，其中Tc、Ta和Tb各为0时分别对应图1中的Ⅰ、Ⅱ和Ⅲ区。

对于确定的Ta、Tb和Tc，零矢量的作用时间为

T0=Ts-max{Ta,Tb,Tc}。

(6)

在三相逆变桥采用七段式SVPWM时三相桥臂的开关作用时间为：

(7)

2 120°坐标系下过调制算法

分析SVPWM算法的调制范围，在Ua和Ub构成的120°区域I，根据式(5)，得Ta=Tx、Tb=Ty、Tc=0，当Ta≤Ts、Tb≤Ts时，根据式(4)，Uα和Uβ满足：

(8)

同理，可以得到区域II和区域III的调制范围内，Uα和Uβ满足：

(9)

(10)

式(8)、式(9)、式(10)其等式构成一个正六边形，正六边形的内部为参考电压可调制区域，如图2所示。

图2 120°坐标系逆变器可调制区域Fig.2 Modulation area of 120° coordinate system inverter

当参考电压矢量的幅值为0.577Udc时，其轨迹为极限六边形的内切圆，内切圆里面的区域为线性调制区，超过内切圆的区域为过调制区域。

当参考电压矢量的幅值为0.667Udc时，其轨迹为极限六边形的外接圆，处于极限六边形的内切圆和外接圆之间的区域为过调制I区，此时参考电压矢量的轨迹一部分在可调制区域，另一部分在极限六边形外，如图3中虚线部分。结合最小相位误差原则，对于可调制区域内的部分，即控制角θ1内的区域保持输出不变，而超出极限六边形的部分限制其输出在可调制区域的边界上，调整后参考电压的输出轨迹如图3中加粗部分。

图3 过调制I区调制策略Fig.3 Modulation strategy of overmodulation region Ⅰ

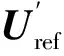
TsUref=TaUa+TbUb。

(11)

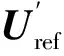
(12)

对比式(11)和式(12)可以得到

(13)

根据式(13)得到调整后的Ub的作用时间，另外几种过调制I区情况与上述相同，不再赘述。

当参考电压矢量的幅值大于0.667Udc时，为过调制II区，其轨迹全部处于极限六边形的外接圆以外，如图4中虚线部分。此时过调制I区的调制策略无法进一步增加逆变器输出电压幅值，为了输出电压最大能到达方波，改进策略为在一定角度内输出电压矢量保持在基本电压矢量，在其他角度区间与过调制I区策略一致，如图4中加粗部分。

图4 过调制II区调制策略Fig.4 Modulation strategy of overmodulation region Ⅱ

在可调制区域OADG边界上添加辅助正三角形ADH和IDG，处于辅助正三角形内部的轨迹按照过调制Ⅰ区的策略处理，外部的轨迹改为保持在基本电压矢量处，保持角为θ2，根据几何关系可知直线IG和AH的Uα和Uβ满足如下：

(14)

根据式(5)可等效为：

(15)

同时，由式(5)可知直线ID和HD的方程为：

(16)

由式(15)和式(16)可以将过调制Ⅱ区分为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ五个区域，处于Ⅰ、Ⅲ、Ⅴ区域的参考电压矢量保持输出为基本电压矢量，处于Ⅱ、Ⅳ区域内调制策略与过调制I区相同，输出被限制在极限六边形的边界上，根据式(17)可以得到调整后的三相作用时间。

(17)

图5 Ta和Tb计算流程图Fig.5 Ta and Tb calculation flowchart

通过这样逻辑判断不需要计算复杂的控制角和保持角，也不需要大量内存占用，计算量很小，配合120°坐标系SVPWM算法可达到最快的运行速度。

为了得到120°坐标系下的参考电压幅值和输出电压基波幅值的关系，定义输出电压调制比M和参考电压调制比M1分别为：

(18)

其中F1为输出电压的基波幅值。

对输出电压进行傅里叶分析，可以得到过调制Ⅰ区和过调制Ⅱ区的基波幅值为：

(19)

(20)

其中θ1和θ2分别为过调制I区和过调制II区的控制角和保持角，根据几何关系可以求得。

结合式(18)，得到调制比M与M1的关系如图6所示。

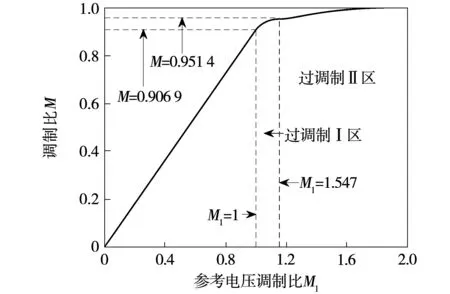
图6 调制比M与M1的关系Fig.6 Relationship between M and M1

从图6中可以看到线性调制区M与M1呈线性关系，过调制区域M与M1呈非线性关系，对于闭环系统，可依靠反馈环节，调节输出电压满足负载需求。

定义谐波畸变率(total harmonic distortion，THD)为

(21)

根据面积等效原理[3]，可以得到过调制I区和过调制II区的输出电压幅值分别为：

(22)

(23)

结合式(21)给出THD与调制比M的关系如图7。

图7 THD与调制比M的关系Fig.7 Relationship between THD and M

从图7中可以看出，由于采用最小相位误差过调制算法，在整个过调制Ⅰ区保持很低的谐波含量，在过调制Ⅱ区逐步增加直到最大，在整个过调制区域THD曲线呈凹陷状，具有优秀的谐波抑制效果。

3 实验验证

为了验证以上提出的过调制算法，搭建了带阻感负载的三相逆变器系统，实验平台以STM32F302R8控制器为核心，主频为72 MHz，开关器件为MOSFET，开关频率为10 kHz，直流母线电压为48 V，负载为三相星型联结的阻感负载R=10 Ω、L=8 mH，通过DL750示波器记录实验波形。实验平台如图8所示。

图8 实验平台Fig.8 Experiment platform

图9为不同调制比下相电压的调制波形。

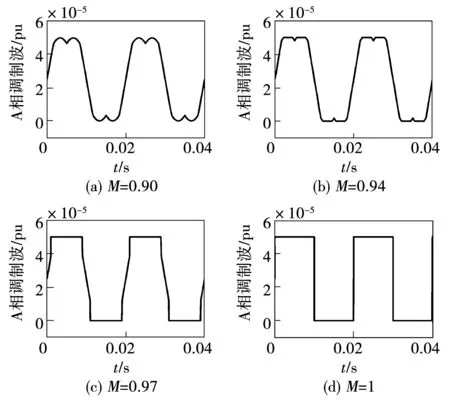
图9 不同调制比下A相调制波形Fig.9 Phase A modulation waveforms at different modulation index

明显看出调制波波形在线性调制区域为标准的马鞍波，进入过调制Ⅰ区，开始出现削顶现象，过调制Ⅱ区，削顶现象到达极限变为类似于梯形波，极限状态下调制波波形也变为了方波。

输出频率为50 Hz、调制比M分别为0.9、0.94、0.97和1的电压，输出线电压Uab和相电流Ia波形如图10所示。

图10 不同调制比下Uab和Ia的波形Fig.10 Waveforms of Uab and Ia under different modulation ratios

可以看出随着调制比逐渐增大，输出线电压斩波的占空比逐步增大直到方波，同时输出相电流的谐波含量也逐步增加，波形发生畸变。

对线电压进行5 kHz滤波，并进行傅里叶分析(fast fourier transform，FFT)后，可得到各次谐波的幅值。其基波幅值和THD值随调制比的变化规律如图11所示,其结果与理论推导基本一致。

图11 基波幅值和THD实验结果Fig. 11 Fundamental amplitude and THD experimental results

为了对120°坐标系和传统六扇区下不同调制区域的计算速度进行比较，图12记录了通过控制器通用输入输出端口(general-purpose input/output ports，GPIO)跳变观测到的程序运行时间，GPIO输出为高电平为算法运行时间。

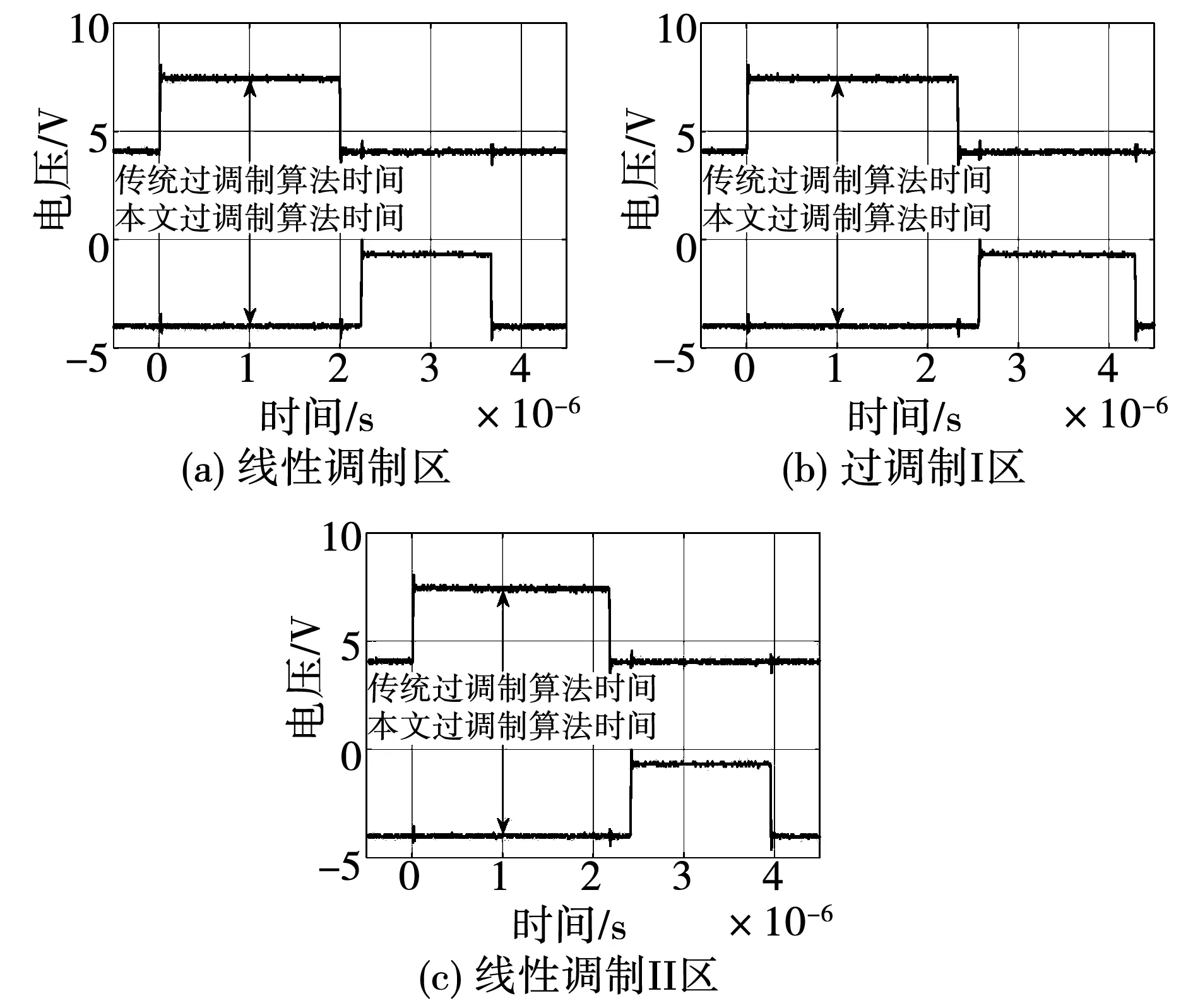
图12 算法时间对比Fig.12 Algorithm time comparison

测得不同调制区域算法运行时间如表1所示。

表1 不同调制区域的运行时间

可以看出，120°坐标系下过调制算法相较于传统六扇区过调制算法，不管是在线性调制区还是在过调制Ⅰ区和过调制Ⅱ区，计算速度都有明显提升，分别节省了27.5%、26.1%和29.6%。

4 结 论

本文结合最小相位误差原则对120°坐标系下的过调制算法展开了研究，推导了过调制I区和过调制II区统一求解模型。算法基于逻辑判断，无需计算控制角和保持角，计算量小。通过实验验证了SVPWM过调制算法的正确性，同时对输出性能进行了测试，结果与理论上基本一致。最后测试新旧算法的计算耗时，结果显示，120°坐标系下的SVPWM过调制算法在全调制区域的运行速度相较于传统六扇区下的算法有明显提升，在保证提高母线电压利用率的同时有更快的运算速度，节省了芯片的计算资源，在一些低成本控制芯片中有很好的工程应用价值。