钢板组合梁桥混凝土桥面板精细化空间分析
2021-06-10屈计划
屈计划
(安徽省交通规划设计研究总院股份有限公司;公路交通节能环保技术交通运输行业研发中心,安徽 合肥 230088)
0 引 言
钢板组合梁桥结构一般设计为“工”字型钢梁,桥面板采用纵横向分块预制,架设后采用湿接缝连成整体,钢梁与桥面板间采用剪力钉连接形成组合受力结构[1,2],钢梁工厂加工,桥面板预制场预制,钢梁与桥面板现场拼接。该种结构形式充分发挥了钢梁与混凝土两种材料的优势,具有结构受力明确、施工方便、节约工期、便于工业化、标准化应用等优点[3,4],代表着工业化技术发展的新方向,提升了公路桥梁的品质,为推动公路建设转型升级,提质增效起到了一定的引领作用。
本文以标准跨径35 m钢板组合梁桥为研究对象,桥梁按35 m简支梁设计,标准宽度14 m,横向布置2片钢梁,间距7.5 m,钢梁采用“工”字型,梁高1.8 m,下翼缘宽1.0 m,上翼缘宽0.5 m,钢梁顶面桥面板采用变厚布置,横向跨中厚度26 cm,钢梁顶面厚度40 cm,桥面板横向分4块预制,于横向跨中及钢梁顶面设置3道现浇湿接缝。两片钢梁间横向每间隔5 m设置一道小横梁,高度0.6 m。钢纵梁及小横梁顶面均设置剪力钉,通过现浇湿接缝与预制桥面板连成整体。该结构形式整体受力方面,桥面板作为结构上翼缘承担压力,钢梁承担拉力。局部受力方面,桥面板为纵向支承间距5 m,横向支承间距7.5 m的双向受力板。以下分析该双向受力混凝土板的空间受力、小横梁支承刚度、桥面板剪力滞效应等结构空间受力性能及影响因素,为桥梁设计提供参考。
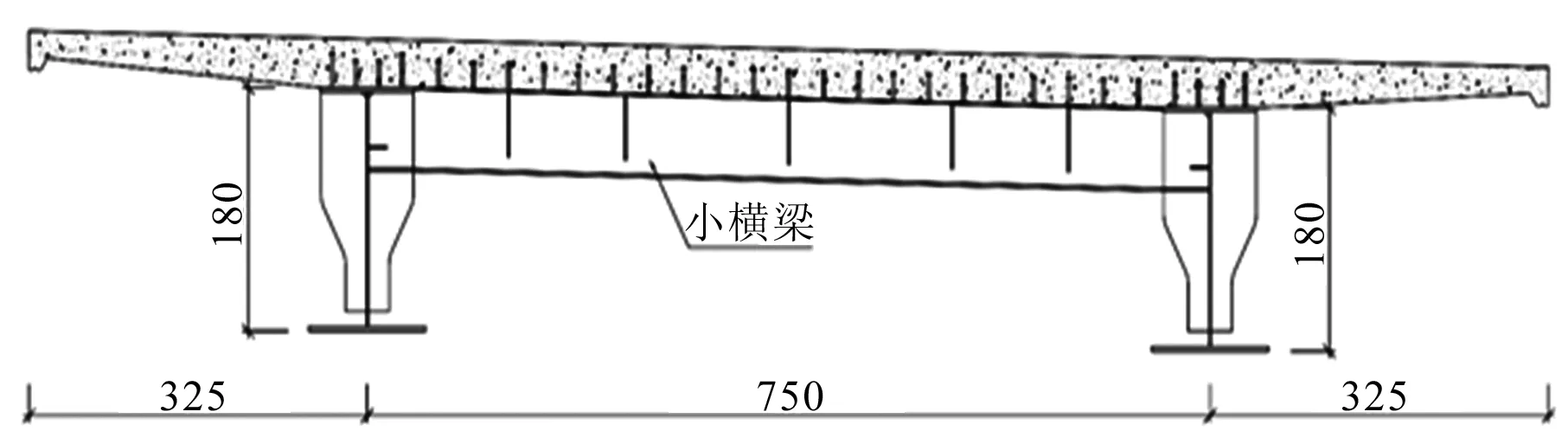
图1 钢板组合梁桥标准横断面(单位:cm)
1 精细化分析模型
模型采用空间网格梁单元模拟[5],横断面上将每道主纵梁及小横梁均离散为单个单元,为重点考虑桥面板受力,桥面板每0.5 m宽度离散为一个单元,单元刚度即为所代表宽度的截面刚度,纵桥向钢梁每2 m离散为一个单元,桥面板每0.5 m离散为一个单元。钢梁重量按实际结构重量设置,桥面板考虑纵、横两方向刚度,重量仅考虑纵梁重量,横梁重量设置为0。钢梁与桥面板间采用刚性连接模拟剪力钉作用。为考虑小横梁支承刚度影响,小横梁高度按0~1.8 m设置(每0.2 m设置为一级),0 m高度即代表该钢板组合梁无小横梁支承,桥面板为横向受力的单向板,小横梁高度1.8 m时与主梁等高。该精细化空间网格梁模型将复杂的桥梁结构离散为多块梁单元受力,每一个节点离散成十字交叉的正交梁格,以十字交叉的纵横划分梁的刚度等代结构刚度,正交梁格之间形成“网”,桥梁整体结构即表达为离散的网格结构,用以进行精细化分析。常规单梁或空间梁模型不能考虑小横梁支承刚度影响,不能考虑桥面板的双向受力模式且不能充分考虑桥面板剪力滞效应,本精细化模型充分考虑了钢纵梁、支承小横梁、剪力钉、桥面板等结构构件的模拟,尤其桥面板网格划分较细,适用于桥面板的精细化空间分析。而桥面板的受力、结构安全及耐久性能直接影响到钢板组合梁桥的全寿命周期使用性能,本模型可以充分考虑钢板组合梁桥结构受力的关键控制因素。
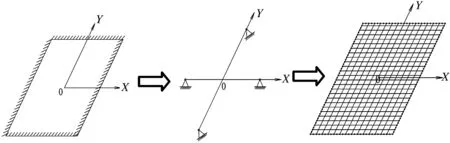
图2 精细化空间网格模型演变示意图
2 桥面双向板受力分析
图3显示了小横梁不同高度条件结构自重作用下混凝土板纵、横两个方向的弯矩。可以看出,混凝土桥面板为双向板受力模式[6],单块板中部跨中纵横向均为正弯矩,单块板钢纵梁及小横梁顶面支承处为负弯矩(支点纵桥向表现为正弯矩,该数值为简支梁纵向整体受力与双向板局部受力叠加,纵桥向简支组合梁桥面板整体表现为负弯矩,上缘受压,实际混凝土板支承处纵桥向局部受力为负弯矩,随着小横梁高度的增加,该正弯矩数值的减少即为局部受力负弯矩的增加)。

图3 双向板纵横向弯矩(单位:kN·m)
由弯矩变化可知,双向板跨中受力主要表现为纵桥向,各种横梁高度条件下,纵桥向跨中弯矩明显大于横桥向弯矩,而板支承位置(即纵横梁钢梁顶面)支点弯矩明显表现出双向受力模式,纵横向支点弯矩均较大。桥面板荷载作用下开裂主要表现为合成主弯矩作用下的裂缝,桥面板按双向板受力模式,跨中部位主弯矩主要沿纵桥向,随着荷载增加,下缘裂缝主要表现为跨中横向裂缝。支点位置下缘主弯矩垂直于对角线方向,上缘弯矩沿对角线方向,随着荷载增加,下缘裂缝主要表现为沿对角线方向,上缘裂缝主要表现为垂直对角线方向。因此随着荷载增加,整块板下缘裂缝发展即表现为由板中部横向裂缝向角点位置扩散发展,上缘裂缝发展主要表现为沿四角垂直对角线方向。
3 小横梁支承刚度影响分析
由图3 可知,随着小横梁高度由0 m变化至1.8 m,双向板纵桥向跨中正弯矩及支点负弯矩均增加(支点负弯矩增加表现为整体受力与局部受力综合正弯矩的减少)。横桥向跨中弯矩和支点弯矩均相应减少,说明随着小横梁高度增加,纵桥向支承刚度增加,纵桥向受力逐步增大,横桥向受力逐步减小,结构受力逐步由横梁高度为0 m时的横向受力单向板模式趋近于小横梁高度为1.8 m时的双向板受力模式。同时可以看出,当小横梁高度由0 m增加至0.6 m时,顺桥向弯矩增加了28%,横桥向弯矩减少了50%;而随着小横梁高度由0.6 m增加至1.8 m,顺桥向弯矩仅增加了8%,横桥向弯矩仅减少了20%。结果说明,桥面板按照双向板受力模式设计,随着小横梁刚度增加,顺桥向受力逐步增大,但当小横梁高度增大到一定程度后结构受力趋于稳定,继续增加小横梁高度将会导致结构用钢量大幅增加,但对结构受力无明显改善作用。所以,结构设计时综合考虑桥面板受力及经济性能,选取小横梁高度为0.6 m。
4 桥面板剪力滞效应分析
小横梁高度按0.6 m计算,纵桥向全桥跨中及1/4跨位置处桥面板各板元轴力横向变化规律如图4所示。

图4 纵桥向不同位置桥面板横向轴压力变化图(单位:kN)
可以看出,桥面板各板元横桥向受力表现出了较大的不均匀性,钢梁顶面桥面板受有较大的压力,由钢梁顶面沿横桥向向跨中及悬臂端部逐渐减小,纵桥向跨中位置减小了24%,纵桥向1/4位置减小了40%,剪力滞效应明显[7]。同时,纵桥向跨中与1/4跨位置减小的幅度差别较大,桥面板剪力滞效应沿纵桥向不同位置表现出了数值的明显不同。
5 结束语
本文建立了钢板组合梁桥精细化空间网格模型分析了混凝土桥面板双向空间受力、小横梁支承刚度影响及桥面板剪力滞效应。精细化模型能够较好的模拟组合结构的各种边界条件及空间受力,混凝土桥面板明显表现为双向板受力特性,中部跨中受力主要表现为纵向弯矩,钢纵梁及小横梁支承处支点受力主要表现为纵、横向双向弯矩,随着荷载增加,双向板跨中裂缝主要沿横桥向,支点下缘位置裂缝主要沿对角线方向发展,支点上缘位置裂缝主要垂直于对角线方向发展。随着小横梁支承高度由0 m逐渐增加到1.8 m,桥面板由横向受力单向板逐步转化为双向受力板,且纵向受力逐渐增加,横向受力逐渐减小,但小横梁支承刚度增加到一定程度后结构受力将趋于稳定,所以结构设计时选取了小横梁高度为0.6 m。沿纵桥向不同位置桥面板横断面上表现出了明显的剪力滞效应,钢梁顶面桥面板轴力最大,向悬臂端部及横向跨中逐步减小,且不同位置剪力滞效应明显不同。本文提供了一种钢板组合梁桥混凝土桥面板精细化计算分析方法,计算结果可为类似桥梁设计提供参考。
