基于高增益观测器的挖掘机工作装置滑模控制
2021-06-10徐国胜於祖庆陆念力吕广明
徐国胜, 於祖庆, 陆念力, 吕广明
(哈尔滨工业大学 机电工程学院,黑龙江 哈尔滨 150001)
挖掘机自动控制一直是工程领域研究的热点。文献[1-4]采用滑模变结构或其与模糊逻辑、自适应理论的结合,调节挖掘机输入转矩,使关节转角跟踪规划值,仿真结果证明了算法有效性。挖掘机工作装置由单活塞杆液压缸驱动,相较于电机驱动的机械臂,由于液压缸系统的非线性,采用关节转矩作为输入,控制不直接且控制精度低,使关节转角实际轨迹与规划轨迹存在很大误差,进而使铲斗斗尖在工作空间不能有效跟踪规划路径。为此,文献[5]分析了某机械臂系统液压伺服驱动空间与关节空间关系,以关节转矩为纽带,建立输入伺服电流与输出关节转角间的数学模型,从而将控制器设计转移到伺服驱动空间。
针对液压伺服系统的控制,阻抗滑模控制[6]、高阶滑模控制[7]、非连续投射[8-9]、及其与滑模控制的结合[10]、反馈线性化滑模控制[11-13],被广泛应用并取得较好的仿真试验效果。然而上述控制方式需要采集活塞杆位移、速度或加速度,以及液压缸两腔压力信号,增加了控制成本。为降低传感器使用数量,观测器被引入至控制器的设计,用来对状态变量或干扰进行观测[14-19]。文献[14]基于投射法对干扰进行观测,文献[15]基于低通滤波对速度观测,文献[16]基于扩张观测器对状态变量及干扰观测,并采用反演法设计液压系统控制器。相较于上述观测器,高增益观测器能够对控制所需的所有状态信息进行有效估计,且设计更为简单,容易实现。文献[17]构造了基于高增益状态观测器的电液系统无源控制器,仿真与试验验证了控制输出活塞杆位移对目标位移信号优良的跟随性能。文献[18]设计了基于高增益观测器的积分滑模控制器,并采用奇异摄动理论证明了闭环系统的稳定性。文献[19]针对电液系统构造了基于高增益观测器的反演控制器,仿真与试验效果较好。
本文通过计算挖掘机关节空间与驱动空间的位移、速度与力之间的关系,得到控制输入伺服阀电压与关节转角之间的关系。采用基于高增益观测器的滑模控制理论,对驱动空间电液系统进行轨迹控制。并采用奇异摄动方法,将观测器状态观测误差与系统控制误差分别作为快变子系统变量与慢变子系统变量,基于李雅普诺夫函数,证明闭环系统稳定。相较于文献[18],本文采用文献[20]中高增益观测器的设计方法,只需调节观测器带宽参数,不需整定其他增益参数,因而观测器设计更加简便;在滑模控制中,采用滑模面函数代替符号函数,消除了抖振且对闭环系统稳定性有重要作用;在液压系统中引入匹配不确定项与非匹配不确定项,通过定义新的状态变量,对非匹配不确定项补偿。仿真结果表明本文设计的基于高增益观测器的滑模控制器效果较好,且对匹配与非匹配不确定项有良好的鲁棒性。
1 挖掘机规划轨迹生成
1.1 挖掘机驱动空间与关节空间关系
图1为挖掘机工作装置模型,采用D-H方法建立了系统坐标。

图1 挖掘机工作装置模型Fig.1 Coordinate frames of the excavator
则挖掘机关节空间关节转角与驱动空间液压缸活塞杆长度之间的关系:
(1)
式中:∠CO1O2、∠AO1x1、∠O1O2B、∠DO2O3、∠GO3O2、 ∠HO3O4、∠EGO2、∠O2GO3与杆长lO1C、lO1A、lO2D、lO2B、lGE、lGF、lO3G、lO3H、lFG、lFH为常量,代入本文研究对象柳工某型液压挖掘样机参数,得到关节转角与对应液压缸活塞杆长度曲线如图2所示。
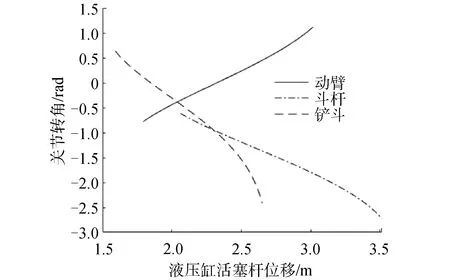
图2 液压挖掘机活塞杆位移与对应转角关系Fig.2 The relationship between piston rod displacement and corresponding rotation angle
由虚功原理,关节转矩与驱动力关系表示为:
(2)

(3)
式中:φ2=θ2+∠CO1O2+∠AO1x1,φ3=θ3+∠O1O2B+∠DO2O3,φ2=θ4+∠EO3O2+∠HO3O4。由式(1),θ4与lEF之间机构连接关系导致雅克比矩阵J中J3项表达复杂,在误差可控条件下,采用θ4与lEH的雅克比关系代替(或直接由图2曲线函数拟合后求导得到对应各关节转角的雅克比项)。
1.2 挖掘机驱动空间轨迹规划
挖掘机不考虑回转时,其铲斗末端轨迹在基坐标系O0x0y0z0(图1)中表示为:
(4)
式中:a1为动臂铰接点水平长度,a2为动臂杆长,a3为斗杆杆长,a4为铲斗杆长,c234=cos(θ2+θ3+θ4),s234=sin(θ2+θ3+θ4)等。以挖掘机整平作业为例,实际中要求铲斗相对设定直线轨迹以固定的切削角进行工作。如图3所示,θd为固定切削角,θb为铲斗齿尖与销轴的连线与切削板的夹角,则铲斗位姿角φ表示为:

图3 挖掘机整平作业铲斗位姿Fig.3 The bucket posture of the excavator during straight-line motion
φ=θ2+θ3+θ4=θd+θb-π
(5)
即φ为固定值。
采用速度规划曲线[21]
(6)
在水平作业面,以切削角θb=π/6进行整平作业(铲斗斗尖从机身远端移动至近端),由几何关系式:
(7)
得到研究对象挖掘机动臂、斗杆与铲斗关节空间角度规划曲线及相应液压缸杆轨迹规划曲线,结果如图4所示。

图4 挖掘机作业面为水平面时的规划曲线Fig.4 Excavator planning curves with horizontal working surface
2 阀控非对称液压缸数学模型
根据文献[22],对挖掘机进行电液比例改造,图5为改造后斗杆阀控非对称液压缸结构框图。PS与PT分别为液压泵供油压力与回油压力,UV为电磁阀阀芯位移,xp=lBD为斗杆活塞杆长度,QA与QB分别表示流入非对称缸无杆腔的流量与流出有杆腔的流量,PA、AA与VA分别表示无杆腔压力,活塞面积与容积。PB、AB与VB则表示有杆腔压力,活塞面积与容积。

图5 斗杆液压系统Fig.5 The schematic of the stick cylinder system
斗杆液压缸力平衡方程为:
(8)
式中:m为活塞杆及腔内液体等效质量;c为活塞杆粘性阻尼系数;k为活塞杆刚度系数。FBD为式(2)中对应于斗杆的驱动力分量。挖掘机在水平作业面按照规划速度整平作业,考虑自重影响不计斗尖阻力时,FBD理论计算结果如图6。

图6 FBD的理论值Fig.6 Nominal value of FBD
斗杆阀控非对称液压缸在不考虑泄露因素条件下的流量连续性方程为:
(9)
式中:VA=VA0+AAxp为无杆腔容积,VB=VB0-ABxp有杆腔容积,VA0与VB0为各腔初始容积,β为液压油液弹性模量。阀的节流方程:
(10)
式中h1与h2为流量增益系数。根据比例伺服阀特性曲线,流量QA和QB与伺服阀输入电压Vin的关系可线性化表示为[23]:
(11)

(12)

3 基于观测器的滑模变结构控制
3.1 滑模高增益状态观测器设计
以斗杆液压缸活塞杆轨迹控制为例,挖掘机在水平作业面整平作业时,采用规划速度曲线得到的斗杆液压缸活塞杆规划轨迹如图4(b)点划线所示。为了降低控制成本,减少传感器使用数量,仅使用位移传感器测量活塞杆实际长度,采用高增益观测器对其他控制状态变量进行观测。为对非匹配不确定项d1(t)补偿,定义状态变量:
(13)
则式(12)转换为:
(14)

(15)

(16)

3.2 滑模控制器设计
根据滑模变结构理论定义滑模面:
(17)
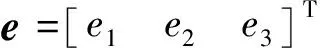
(18)
设计控制输入u为:
(19)

(20)
3.3 闭环系统稳定性


(21)

(22)
则状态变量η与s可表示为奇异摄动标准形式:

(23)
式中:η为快变子系统状态变量;s为慢变子系统状态变量,且


(24)
定义李雅普诺夫函数:
(25)
则有:
(26)
易知V指数收敛,且在有限时间内V=0⟹s=0,
(27)
因为Ae为Hurwitz,则跟踪误差e有限时间指数收敛。将式(23)时间尺度变换为τ=t/ε,则系统变换为:
(28)
当ε→0,式(28)表示为:
(29)
因为A是Hurwitz,存在正定矩阵Pη使得:
ATPη+PηA=-I
(30)
定义李雅普诺夫函数为:
Vη=ηTPηη
(31)
则其对时间尺度τ的微分:
(32)

3.4 仿真

d(t)=(-89.1t4+1142.16t3-4 805.82t2+
7 149.8t+157.09)/160+100cos(2t)+
100sin(5t)/160
(33)

3 574.90t2-157.09t+20 816.56)/160


图7 κ=100时ε对观测误差的影响Fig.7 The state estimation errors of high-gain observer with κ=100
由图7易知,在不考虑系统噪声环境下,ε值越小,对非匹配不确定项与匹配不确定项补偿效果越好,观测误差越小。由图8和图9,κ值越大,闭环系统收敛越快。

图8 ε=0.001不同κ值的轨迹跟踪效果Fig.8 The tracking performance of the HOSMC with ε=0.001

图9 ε=0.001时不同κ值的轨迹跟踪误差Fig.9 The tracking error of the HOSMC with ε=0.001
4 结论
1)通过建立挖掘机关节空间与驱动空间关系,以液压缸杆规划曲线为跟踪目标,伺服阀输入电压为控制输入,使控制方式更加直接,易于实践。
2)以斗杆活塞杆轨迹控制为例,采用高增益观测器减少了传感器使用数量,降低了控制成本。观测器只需设计增益带宽ε,设计参数少,方法更为简便。在滑模控制中,通过对输入切换项的符号函数采用滑模面函数代替,消除了抖振。闭环系统通过奇异摄动理论验证了稳定性,跟踪误差有限时间收敛。
3)对于式(12)型的一类系统,通过定义新的状态变量,采用基于高增益观测器的滑模控制时,可选择较小的带宽参数ε与较大的κ值,满足控制需要。对于挖掘机其他液压缸的控制,在进行流量分配后,可类似斗杆液压缸系统进行分析控制。
