西学东渐与三角函数表在中国的传入与调适*

李亮

明清之际，西洋传教士来华及西学东渐，给中国带来了大量的西方科学技术和思想，是近代中外文化交流的一个重要方面。然而，由于中西科学知识体系的不同，使得早期的交流与融合面临着诸多困难。尤其对于中国历算家来说，当时传入的西学知识中，最难接受的便是三角学。一方面，是因为中国古代数学缺乏一般角的概念，以及球面三角学等知识，即“未有予立算数以尽勾股之变者”。(1)《自然辩证法通讯》杂志社编：《科学精英：求解斯芬克斯之谜的人们》，北京：世界图书出版公司北京公司，2015年，第512页。清代历算家梅文鼎(1633—1721)曾指出传统《授时历》中存有弧矢割圆之术，其精华“剖析浑体，于无勾股中寻出勾股”，大体与西方球面直角三角学有着类似的功能。不过，有研究认为这与球面三角法依然有着根本上的区别。(2)郭书春主编：《中国科学技术史·数学卷》，北京：科学出版社，2010年，第 419页。而这种差异也有着思想上的根源，如李约瑟就认为“中国人的数学思想与实践一贯是代数学的，而不是几何学的”。(3)[英]李约瑟：《中国与西方的科学与社会》，载潘吉星主编：《李约瑟文集》，沈阳：辽宁科学技术出版社，1986年，第71页。

另一方面，中国传统数学也缺乏与三角学相对应的计算表格。清代数学家安清翘(1756—1829)就曾指出“古勾股、弧矢之术，于理已尽，于法亦无不足，所少者未曾立表耳”，而当时很多著作因不能立表布算，导致这些书“既不能布算，是无用之书也”(4)[清]安清翘：《一线表用》，《数学五书》本。。虽然中国传统数学已有勾股术和弧矢术，然而与勾股、弧矢相关的三角函数表却是自明末由西方引入的。

在明末，徐光启就曾强调三角函数表的重要性，并将其命名为“大测表”(后改称“八线表”)，认为“其数之多，其用之广，于测量百法中皆为第一，故名大测”(5)[明]徐光启：《崇祯历书·割圆八线表》，韩国首尔大学奎章阁图书馆藏。。清末数学家徐有壬(1800—1860)也称其“万算皆从此出，表之用大矣”(6)[清]徐有壬：《务民义斋算学·造各表简法》，清光绪九年刊本。。

最早系统介绍三角函数和三角函数表的中文专著是德国耶稣会士邓玉函(Johann Schreck，1576—1630)的《大测》，该书以德国数学家毕的斯克斯(Bartholomeo Pitiscus, 1516—1613)《三角法》的1612 年版本作为底本，并且参照了比利时数学家斯蒂文(Simon Stevin，1548—1620)的著作《数学记录》，将西方三角学知识总结成“六宗”“三要”“二简法”“四根法”。(7)董杰、陈建平：《中国第一部三角学译著<大测>的底本与版本研究》，载《中国科技史杂志》2017年第2期，第173—185页。不过，在《大测》出版之前，一些零散的三角学知识就已陆续传入中国，其中就包括一份名为《同文算指别编》的著作。书中记载的八位数据弦表，则是近代西方三角学和三角函数表传入中国之首。这份弦表主要用于黄道坐标、赤道坐标和地平坐标之间的换算，以及日出入时刻和晨昏时刻的推算等。只因该书当时并未出版，所以一直未引起学界的关注。

另外，虽然三角函数表在天文、航海和大地测量等领域有着广泛的运用，但由于中西知识体系之间的隔阂，导致明末对三角函数表的编算和使用存有不小的争议。甚至入清之后，有些争议还一直存在。本文从三角函数表传入和调适的角度，对《同文算指别编》进行介绍，分析和考证其内容来源，并且对明末清初中国引入和会通西方三角函数表过程中，引起的问题以及引发的争议进行分析和讨论。

一、《同文算指别编》及其弦表

《同文算指》是意大利耶稣会士利玛窦(RicciMatthieu，1552—1610)和李之藻(1565—1630)合作编译的一部影响甚大的数学译著。数学史家钱宝琮曾指出：“《同文算指》书在西学东渐史中与徐光启所译之《几何原本》六卷皆为极重要之著述，而所收成效尤在《几何原本》之上”(8)钱宝琮：《浙江畴人著述记》，载《钱宝琮科学史论文选集》，北京：科学出版社，1983年，第307页。。该书分为《前编》《通编》和《别编》三部分，前两部分于1614年左右出版，据李之藻《同文算指前编》序记载“荟辑所闻,厘为三种：《前编》举要,则思已过半；《通编》稍演其例,以通俚俗,间取《九章》补缀,而卒不出原书之范围；《别编》则测圜诸术,存之以俟同志”(9)[明]李之藻：《<同文算指前编>序》，载《中国科学技术典籍通汇·数学》卷4，开封：河南教育出版社，1993年，第79页。。其中，《前编》介绍了自然数、小数的笔算加减乘除四则运算的方法；《通编》叙述了分数、比例、级数求和、盈不足、方程、开带以平方等算法，为全书的核心。(10)邹振环：《<同文算指>的译述及其意义》，载《上海科技翻译》1990年第2期，第45页。这些内容被认为是根据利玛窦的老师克拉维斯(Christopher Clavius，1537—1612)在1583年出版的《实用算术概论》(EpitomeArithmeticaePracticae)一书编译(11)钱宝琮：《中国数学史》，北京：科学出版社，1964年，第236页。，此外，还参考了中国数学家程大位的《算法统宗》(12)[日]武田楠雄：《<同文算指>の成立》，载《科学史研究》，1954(30)，第7—14页。和周述学的《神道大编历宗算会》(13)潘亦宁：《中西数学会通的尝试——以<同文算指>(1614年)的编纂为例》，载《自然科学史研究》2006年第3期，第215—226页。等书。

《同文算指》出版时只包含《前编》二卷和《通编》八卷，《别编》并未一同刊印，因此不广为人知。以至于早期的学者甚至怀疑《同文算指别编》就是《圜容较义》，只因其刻本单行，故不称别编。(14)钱宝琮：《浙江畴人著述记》，载《钱宝琮科学史论文选集》，北京：科学出版社，1983年，第285页。后来，数学史家李俨发现了法国国家图书馆所藏《同文算指别编》抄本(馆藏号为Chinois 4862，后称《别编》),并于1935年由王重民赴巴黎整理敦煌史料工作期间，代为复制回国。(15)当年摄制的照片目前保存于中国科学院自然科学史研究所“李俨图书馆”(馆藏号：善子530.9915/302)。近年来，这些照片又被重新处理和整理，收录于《中国科学技术典籍通汇·数学》卷4。《别编》抄本署名“西海，利玛窦授；浙西，李之藻演”(16)[明]利玛窦、李之藻：《同文算指别编》，法国国家图书馆藏抄本。，内容只有“截圜弦算”一节(图1)。全书开篇介绍了西方三百六十度“平度”制，以及“弦”“弧”和“全数”等概念，并给出了“弧”和“弦”之间的六种用法。(17)即“有以弧度分求正弦数者；有以弧度分求余弦数者；有以正弦数求弧度分者；有以余弦数求余弧度分者；有以弧度分求弦倒数者；有以弦倒数求弧度分者”。

图1 《同文算指别编》首页(左)和封面(右)(法国国家图书馆藏)

从内容来看，书中有多处删改和润色的痕迹，可能属于当时编译用的一个“工作本”。其主体内容是一份弦表，但该书并没有完整抄录弦表全部内容，只是给出了表格首尾两页，且每页也只示范性地列出了首尾几行的数据。不过，在弦表首尾两页之间预留了足够的空白页，显然是为了以后补充所用(图2)。(18)中国科学院自然科学史研究所藏该书照片算表页有王重民标注的“原书此处有白纸数十页。重民记”字样。

图2 《同文算指别编》中的弦表

除了表格之外，该书还详细介绍了如何使用该表进行十种不同的天文计算，包括：

(1)推黄道度离赤道法。

(2)以北极度推日出入时所离卯酉中地平度法。

(3)以日出入时所离卯酉中之平度推此极出地度法。

(4)推每日太阳最高度法。

(5)推半昼分法。

(6)以时刻推太阳离地平度法。

(7)以太阳离地度分推时刻法。

(8)推朦胧景时刻法。

(9)以各宿距黄道度求距赤道度法。

(10)以黄道经度求所值赤道经度法。(19)[明]利玛窦、李之藻：《同文算指别编》，法国国家图书馆藏抄本。

从中可以看出，这些计算主要涉及黄道坐标、赤道坐标和地平坐标之间的换算，以及与之相关的日出入时刻和晨昏时刻的推算等问题，属于球面三角学知识。并且每个问题都是首先介绍计算步骤，然后以 “假如”(即算例)的形式给出具体推算方法。

此外，各问题之后所附算例，不但前后关联，也非常具有针对性。例如，这些“假如”都是以“金牛二度”为例，有的算例在计算时还需要调用前一算例中的相关结果。地理纬度则统一以“京师北极出地四十度”为例，时间也一致采用“万历庚子(1600)”。而且还以此对恒星位置进行了岁差修正，如文中提到“假如大角经度原离白羊一百七十度二十分，今于万历庚子测之，加岁差二十七度四十七分”。(20)[明]利玛窦、李之藻：《同文算指别编》，法国国家图书馆藏抄本。

总体而言，该书在内容上除了仅对“弧度”“正弦”“余弦”和“弦倒数”(21)“弦倒数”即现代三角学中的“矢”，《崇祯历书·大测》记载“倒弦者，余弦与全数之较，本名矢”。等概念做了简单说明外，并没有系统地介绍三角学的理论知识，以及给出算表的编算方法。而是以问题的形式来介绍，如何通过弦表直接进行相关天文计算，可以说是一本极具实用性和操作性的三角学小册子。

《别编》全书主体内容都是介绍如何使用正弦和余弦表进行天文学中的球面三角计算。由于是首次将西方的三角算表介绍到中国，为了让读者能够熟悉算表的结构和使用方法，该书还在弦表之前，对其编排方式和用法做了详细介绍，其内容如下：

后列横表每二副，搃作一副。观而置右副居上，左幅居下，相联定算。首层所排〇、一、二、三顺行至八十九，皆正弧度，末层所列自八十九逆数至一、〇皆余弧度，相交对。其每幅右行所顺列自〇、一、二、三以至六十为正弧度之细分，左行所倒列自六十至三、二、一、〇为余弧度之细分，亦相交对。其中间自第二层至三十一层所列，皆本度本分之弦也。(22)[明]利玛窦、李之藻：《同文算指别编》，法国国家图书馆藏抄本。

中国传统数学和天文算表一般很少在表前给出专门的解释性文字，这份弦表由于译自西方著作，其排列方式和用法也都符合西方的习惯，所以书中对其编排结构逐一做了说明。

其中，还使用了此前中国传统算表中较少使用的“副”“层”和“行”等术语。“副”大致相当于一页，即表的每部分都由上下两幅组成，右副居上，为〇到三十分即各度前三十分的数据，左幅居下，为后半部分的数据。“层”表示算表的各个横行，表中每副共有三十三层，首层和末层分别顺行和逆行列出从〇至八十九各个度数，中间的三十一层为对应的〇至三十或者三十至六十分的正弦和余弦数值。

这份弦表将正弦和余弦数值置于一份表中，利用对称结构，使其数据能够被共享，以节约表格篇幅。从不同方向读取表格，可以分别实现正弦和余弦的读数操作。这种如今看起来司空见惯的表格形式，在西方算表传入中国之前却是显得非常“另类”。这种利用表格数据的对称性，从正反两个不同方向读取表格的西方算表形式，也被称之为“旋转对称”(Rotational Symmetry)结构。(23)Li Liang,“Tables with ‘European’ Layout in China: A Case Study in Tabular Layout Transmission”,International Journal for the History of the Exact and Natural Sciences in Islamic Civilisation,issue 13,2014:pp.83-101.这种结构对此后中国数学和天文算表产生了深远的影响，不仅在清代的各种算表中被广泛运用，甚至在《明史·历志》中还被用于改编《回回历法》等内容。(24)Li Liang,“Arabic Astronomical Tables in China: Tabular Layout and its Implications for the Transmission and Use of the Huihui Lifa”，East Asian Science, Technology,and Medicine,No.44，2016:pp.21-68.

该表的另一特点是使用了八位数据，以“一〇〇〇〇〇〇〇”(即一千万)为全数(即圆半径)，书中提到“其径即环半径，割谓一千万分，谓全数。凡数弥析弥精，更衍之，当不止此。然析至千万见大凡矣，故名全数也”(25)[明]利玛窦、李之藻：《同文算指别编》，法国国家图书馆藏抄本。。弦表全数即半径越大，算表的位数越多，数据也就越精确，该书采用一千万为半径，认为千万分最为常见，这也是当时西方弦表最为常用的标准之一。

二、弦表的发展及《别编》来源

在西方传统中，古希腊、印度和阿拉伯科学家很早就利用三角学知识，构建出不同的算表以辅助计算。尤其是通过运用三角学和球面三角法知识，用以解决天文、航海和大地测量等领域的各种问题。与其他古代文明注重几何模型不同，中国传统天文学主要利用代数方法解决三角学上的问题，所以对三角函数表的需求并不十分迫切，相对西方的发展也比较滞后。

公元6世纪时，一些印度天文学和数学书籍随着佛经一起传入中国，其中就包括印度弧度度量法及球面三角法等。《开元占经》(718)所载《九执历》就记载有一份当时传入的正弦表。(26)田淼：《西方数学知识在中国的传播——中国数学家对三角函数概念及公式的研究》，载《中国数学的西化历程》，济南：山东教育出版社，2005年，第278—325页。此外，天文学家僧一行(683—727)在其编修的大衍历(724)中，也构造有一张晷影差分表, 被认为是最早的正切函数表。(27)刘金沂、赵澄秋：《唐代一行编成世界上最早的正切函数表》，载《自然科学史研究》1986 年第4期，第298—309页。不过这些著作虽然将类似于三角学的计算表格化，但并不是严格意义上的三角函数表，且未能引起中国数学家和天文学家的重视，也没有产生显著的影响。16世纪末，随着西学东渐和明末历法改革的推进，西方三角学知识依托于天文学再次传入中国，对中国数学和天文等科学的发展产生了深远影响。

西方弦表起源于古希腊，不过严格意义上的现代弦表15世纪之后才正式出现。古希腊数学家希帕恰斯(Hipparchus, 约前190—前120)最早给出了计算指定圆弧所对应弦长的方法, 之后经过托勒密(Claudius Ptolemy，约100—170)的发展，编算成半径为60，间隔为半度的弦表，并收入其《至大论》(Almagest)第一卷中。

托勒密之后的相当长时间内，弦表并没有得到重视和发展，直到德国天文学家雷乔蒙塔努斯(Iohannes Regiomontanus，又名 Johannes Müller，1436—1476)于1463年左右编写了一份共计三十页，半径为60000，间隔为1角分的弦表。(28)不过，直到1490年该表才在其著作Tabulæ Directionum Profectionumque中出版。Johannes Regiomontanus,Tabulæ Directionum Profectionumque,Augsburg: Erhard Ratdolt, 1490.为了提高精度，雷乔蒙塔努斯于1465年又将弦表的半径增加至6000000。随后，为了计算方便，他又对弦表进行了改进，在1468年完成了半径为10000000(八位)的弦表(29)Folkerts, Menso, Regiomontanus als Mathematiker, Centaurus,1977(3-4):pp.214-245.，这项工作也奠定了以后弦表的基本形式。

在相当长时间里，西方编撰的各类弦表都是直接或间接来自雷乔蒙塔努斯。例如，德国学者阿皮安(Peter Apian，1495—1552)就将雷乔蒙塔努斯弦表的半径简化到100000(六位)。(30)Peter Apian, Introductio Geographica, Ingolstadt,1533.此外，哥白尼(Nicolaus Copernicus，1473—1543)也在其基础上，完成了一份共计三十六页，间隔为1角分的八位弦表。(31)Nicolas Copernicus,De lateribus et angulis triangulorum, tum planorum rectilineorum, tum sphaericorum, libellus eruditissimus & utilissimus.Wittemberg: Johannes Lufft, 1542.同时，哥白尼在其《天体运行论》中也给出了一份进行简化的，间隔为10角分的五位弦表。(32)Nicolas Copernicus，De revolutionibus orbium coelestium.Nuremberg:Johannes Petreius, 1543.

哥白尼的门徒雷蒂库斯(Georg Joachim Rheticus，1514—1574)则将弦表计算推向了极致，他一生中最主要的工作除了帮助哥白尼出版《天体运行论》，就是进行三角算表的编算。因其将毕生精力都投入算表的编算中(33)雷蒂库斯不但出版了最早的正割表，还首次使三角算表的编排间隔达到一角分以下。，雷蒂库斯也被认为是“二十世纪之前最伟大的数学算表编算者”(34)Archibald R C, Rheticus, with special reference to his Opus Palatinum,Mathematics of Computation,1949,3(28):pp.552-561.。他认为当时造成观测误差的主要原因，已经不再是仪器的精密与否，而是三角算表中不断累计的误差所致，于是立志编算间隔为10角秒的十一位弦表。然而，这项工作一直到他死后，才由他的门徒瓦伦廷(Valentinus Otho，1550—1603)继续完成。雷蒂库斯甚至还试图编算一份间隔为10角秒，半径为十六位的弦表，但这一目标直到1613年才由皮提斯卡斯(Bartholomaeus Pitiscus，1561—1613)实现。

《别编》八位弦表由利玛窦传入中国，由于利玛窦介绍至中国的《几何原本》《测量法义》《圜容较义》等西方著作，都是直接或间接源自克拉维斯。(35)克拉维斯被利玛窦称为丁先生，徐光启在“刻《几何原本》序”中说：“利先生从少年时，论道之暇，留意艺学，且此业在彼中所谓师传曹习者，其师丁氏，又绝代名家也。”并且《同文算指》前编和通编的主要内容亦是源自克拉维斯(36)《几何原本》《测量法义》《圜容较义》《同文算指》前编和通编的主要内容分别来自克拉维斯的Euclidis elementorum libri XV(1574);Geometria practica(1604);In sphaeram Ioannis de Sacro Bosco commentaries(1570);Epitome arithmeticae practicae(1583)。，所以可以推断，这份弦表很可能来源也相似。当时，在西方出版八位弦表著作的数学家屈指可数，克拉维斯便是其中一位。克拉维斯多部著作中都有与《别编》弦表非常相似的算表(图3)。(37)例如，克拉维斯的著作Astrolabium(1593); Theodosii Tripolitae Sphaericorum libri tres(1558);Opera Mathematica(1612) 和Tabulœ Sinuum, Tangentium Et Secantium, Ad partes radij 10,000,000(1607)。此外，克拉维斯也指出，其弦表也是在雷乔蒙塔努斯的基础上修订而成。

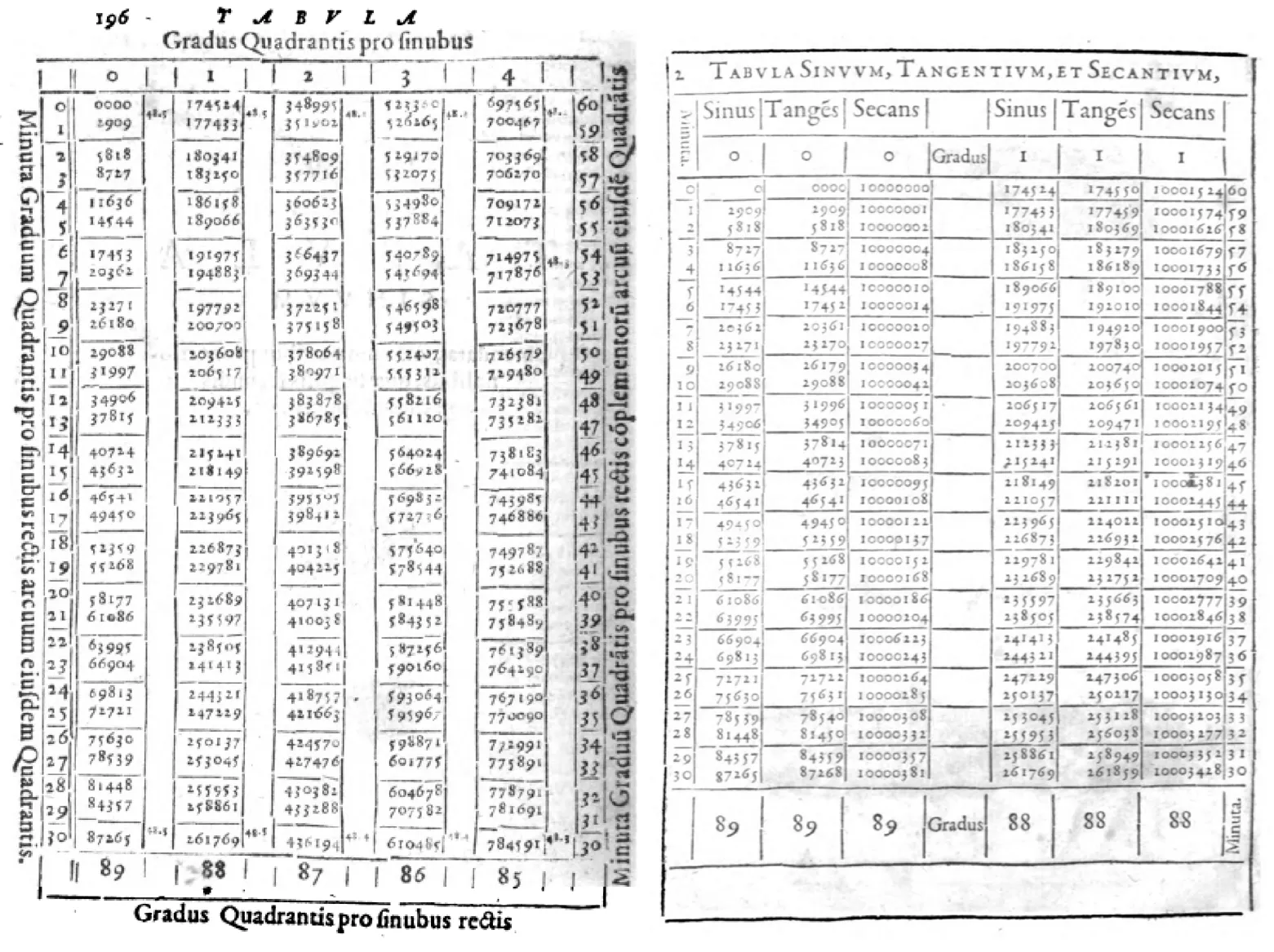
图3 克拉维斯著作中的弦表(38)左图源自Astrolabium，右图源自Tabulœ Sinuum, Tangentium Et Secantium, Ad partes radij 10,000,000。

在克拉维斯的各种著作中，与《别编》在内容和性质上最为接近的是1607年出版的一本手册(39)该书全名为Tabulœ Sinuum, Tangentium Et Secantium, Ad partes radij 10,000,000.& ad scrupula prima Quadrantis, Et ad earum praxin breuis introductio, ex pleniore Tractatu。大意为《半径为一千万的正弦、正切和正割及其简要使用手册》。，名为“TabulœSinuum,TangentiumEtSecantium,Adpartesradij10,000,000”。(40)该书原书包括“Typographus Ad lectorem”(序言)、“Definitions”(定义)、“Observationes”(惯例)、“Exposition partium tabulae”(表的一些解释)、“Usus tabularum in sinibus”(正弦表的使用)和“Usus tabularum in tangentibus & secantibus”(正切和正割表的使用)。其中“Definitions”部分简要介绍了“Chorda”(弦)、“Sinvs rectus”(正弦)、“Sinus versus”(倒弦)、“Complementum sinus versi”(倒余弦)、“Complementum arcus”(余弧)、“Sinus complementi”(余弦)、“Sinus totus”(半径，即全数)、“Tangens”(正切)、“Secans”(正割)。“Exposition partium tabulae”部分则与《同文算指别编》一样介绍了表的编排结构和查表方法。该书与《别编》不同之处，一方面只是《别编》还介绍有弦表在天文计算中的运用，并且给出了具体算例；另一方面，《别编》并没有和弦表一起给出切线和割线的算表。因此，与《同文算指》的前编和通编一样，《别编》很明显也不是单一的直译克拉维斯的某部著作，其天文计算部分应该参照了其他相关著作，而算例应该是根据中国京师的位置和万历年间的天象重新编算而成。

至于《别编》为何没有最终出版，可能与利玛窦于1610年去世有关。李之藻与利玛窦于1601年相识(41)李之藻于1601年，在利玛窦留居北京不久，便去拜访，他曾在《职方外纪序》中提到：“万历辛丑(1601)，利氏来宾，余从僚友数辈访之。”参见[明]李之藻：《天学初函 编器 下》，黄曙辉点校，上海：上海交通大学出版社，2013年，第1352页。，从其学习西方天文﹑数学﹑地理等知识。因为聪颖勤奋，李之藻很快地掌握了这些新知识，利玛窦在其《札记》中也提到“他(李之藻)掌握了丁先生(Father Clavius，即克拉维斯)所写的几何学教科书的大部分内容”(42)[意]利玛窦、[法]金尼阁著：《利玛窦中国札记》，何高济等译，北京：中华书局，1983年，第432页。。不久两人以“耳受手书”的方式(43)李之藻在《浑盖通宪图说自序》中记载有：“昔从京师识利先生，欧罗巴人也，示我平仪。……得未曾有，耳受手书，颇亦镜其大凡。”合作完成了《浑盖通宪图说》(44)《浑盖通宪图说》于1605年开始编译，1607年刻印出版。(1607)和《圜容较义》(1608)两书(45)利玛窦在1608年8月2 日给罗马耶稣会总会长阿桂委瓦神父的信中提到“跟我学习数学已经好久了，今年再印刷《浑盖通宪图说》, 是我恩师丁先生神父的Astrolabio 的节译本, 由我口授而他笔录”，“现在他已回到北京, 准备印刷丁先生恩师的《同文算指》 (Arithmetica Practica) 及《论钟表》(De Horologiis)两书”。参见[意]利玛窦著：《利玛窦书信集》，罗渔译，台北：光启出版社，1986年，第366页。。随后，两人又开始了《同文算指》的编译。李之藻在《同文算指》序中说也提到“往游金台，遇西儒利玛窦先生”，利玛窦与其“精言天道，旁及算指”，李之藻因“喜其便于日用”，随即决定翻译此书。与此同时，利玛窦也不断写信要求罗马教廷给他寄送最新的数学书籍。

1610年，利玛窦过世，次年李之藻亦因其父去世而回家乡守丧，《同文算指》的出版事宜一再拖延。虽然《前编》和《通编》几年后陆续出版，但由于《别编》只有“截圜弦算”一节，属于尚未完工的著作，书中介绍的平面三角学知识，与后面举例的球面三角学内容，在体例上也不太一致。因此，利玛窦去世后，李之藻可能难以独自继续完成该书，最终只留下了这部“半成品”。

三、三角函数表在中国的引入和调适

《别编》作为最早将西方弦表及其使用方法介绍至中国的著作，因并未出版，所以在当时影响比较有限。中国最早正式出版的一批三角学著作主要有邓玉函的《大测》《割圆八线表》和罗雅谷(Giacomo Rho，1593—1638)的《测量全义》。这些著作大约完成于1631年左右，皆属于《崇祯历书》的一部分。(46)崇祯四年(1631)正月二十八日徐光启在第一次进呈的书中正式提交了《大测》二卷、《割圆八线表》六卷和《通率表》二卷等。《测量全义》十卷则属于崇祯四年八月初一日第二次进呈的书目之一。然而，由于中西知识体系之间的差异，其出版过程也并不顺利，在使用习惯以及编算方法等方面都面临着不小的争议。

《崇祯历书》中保留有两份早期的三角函数表，一份为《割圆八线表》中间隔为1角分的六位算表，另一份为《测量全义》卷3中的“割圆八线小表”(间隔为15角分的五位算表)。这里的“小表”是相对“大表”和“中表”而言(47)如《治历缘起》曾提到有《黃道升度立成中表》四卷，今已不得见。，其区别在于“大表之全数或八位或九位、十位，今小表止全数六位，以便推算”(48)[明]徐光启：《崇祯历书·割圆八线表》，韩国首尔大学奎章阁图书馆藏明刊本。，即不同位数的表格用于满足不同精度需求的计算。

据《治历缘起》记载，崇祯三年(1630)主持历法改革的历局已完成 “书表稿草一十九卷”，其中就包括《测圆八线立成长表》四卷和《通率立成表》一卷等。不过，崇祯四年(1631)正式进呈崇祯皇帝时，书目中包括有《割圆八线表》六卷和《通率表》二卷。(49)[明]徐光启：《崇祯历书·治历缘起》，美国哥伦比亚大学藏明刊本。然而，《崇祯历书》正式刊印时却仅有《割圆八线表》一卷。可见，当时编算的《长表》等最终都并未付梓。

另据《学历小辩》记载，最初编修《大测》时“有《立成》，有《通率》，都为一十六卷，八十余万言”(50)[明]徐光启：《学历小辩》，日本国立公文书馆藏本。,可见其内容之多，工作量之巨大。《大测》中亦提到使用算表可以“不劳余力，不费晷刻”，但是同时 “为之者劳，用之者逸”(51)[明]徐光启：《崇祯历书·大测》，韩国首尔大学奎章阁图书馆藏明刊本。。此外，徐光启也指出，诸表的编算“此则今之愈繁，乃后之愈简，以臣等之甚难，开诸臣之甚易，何足畏哉？”(52)[明]徐光启：《崇祯历书·治历缘起》，美国哥伦比亚大学藏明刊本。表明了这些算表的编算工作在当时虽然艰巨，但编成后便可以一劳永逸，使用极为便捷。

三角八线表的使用也大大促进了明末历法改革的进程，以及《崇祯历书》的编修工作。崇祯二年(1629)，徐光启在改历之初就提到“如旧用测圆术，求距度一率，即须展转乘除，穷日之力。而臣等翻译原文二万一千六百率，又改从大统加减演算为三万六千率，用之，推步展卷即得”。他还指出“新法立成其种以百计，一种之率大者以万计，傥用其旧术，当聚数十人推算二三百年乃可竣事，将何以应诏称任使乎”(53)[明]徐光启：《学历小辩》，日本国立公文书馆藏本。。因此，在徐光启看来，倘若使用传统的弧矢割圆术进行推算，动辄上万格的篇幅，几乎无法在短期内完成。

由于三角八线表 “推步展卷即得”的特点，使其不仅得到历局的追捧，甚至一些反对西法的传统历算家也不排斥将其作为一种工具来使用。例如，徐光启曾批评魏文魁 “尤用周三径一，开方求矢之法”，认为他固执地坚持中国传统弧矢割圆术。魏文魁则答复：“弧矢割圆三乘之误，贵局定有良见著为书，何如使魏收入《历元》以传后世？”(54)[明]徐光启：《学历小辩》，日本国立公文书馆藏本。可见，即便魏文魁这样的保守派，也希望徐光启能将西方三角之法公诸于世。当然，徐光启自然不愿与其分享这一利器，只是略带嘲讽的回应他：“老而好学，诚往昔之美谈。然求人之术，乃当以排抵为羔雁耶？”并指出历局编译的算表多达八十余万言，如果“以入《历元》得无本末不相称耶？此书为用甚大，故名《大测》，自当孤行于世，待知者用之”。(55)[明]徐光启：《学历小辩》，日本国立公文书馆藏本。

图4 《崇祯历书·通率表》朱补遗抄本(日本天理大学藏)

从《崇祯历书》最终的出版情况看，其三角八线表还是放弃了传统百进制，选择全盘接受西法的六十进制。一方面，可能是这样的转换，无疑加大了推算的工作量，且使用不便。另一方面，可能是徐光启等人在修历中意识到“会通”的难处，中国的勾股术和以三角为基础的西方割圆八线法并不完全相容。如祝平一就认为，放弃周天度而统一使用平度360度，正是历局策略调整之一。这样会使以往《大统历》所使用的各类立成表形同废物，以迫使传统历法的支持者放弃中法，从而接受西法。(59)祝平一：《三角函数表与明末的中西历法之争——科学的物质文化试探》(上)、(下)，载《大陆杂志》1999年5月：第41—48页；1999年6月，第9—18页。

其实，关于三角函数表的编算到底采用六十进制还是百进制，至清代还一直存有争议。例如，清初历算家薛凤祚(1599—1680)在其《天学会通》(60)《天学会通》原题名《历学会通》，部分内容收入《四库全书》后避讳改名。中就编撰有百进制的三角函数，认为“今有较正会通之役，复患中法太脱略，而旧法又以六成十不能相入，乃取而通之，自诸书以及八线皆取六数通以十数”(61)[清]薛凤祚：《历学会通·中法四线引》，益都薛氏遗书本。。梅文鼎对其采用百进制，以此与传统《授时历》保持一致的做法，给予了充分肯定，认为“是书亦称其以西法六十分通为百分，从授时之法，实为便用”。(62)李亮、石云里：《薛凤祚西洋历学对黄宗羲的影响——兼论<四库全书>本<天学会通>》，载马来平主编《中西文化会通的先驱“全国首届薛凤祚学术思想研讨会”论文集)》，济南：齐鲁书社，2011年，第218—230页。然而，清代数学家江永(1681—1762)对此却提出了不同看法，指出“薛仪甫(即薛凤祚)著《天学会通》改六十分为百分，则当先改八线表，而余诸表皆不可用，亦觉更张多事”(63)[清]江永：《数学》卷1，《丛书集成初编》本。。他认为薛凤祚虽然将三角函数表转为百进制，这却给其他各种六十进制表的使用带来了极大不便，明显多此一举。

结语

16世纪，随着新航路的开辟，欧洲传教士络绎东来，开启了中西文化交流的序幕，西方近代科学随之不断传入中国。当近代科学与中国传统科学接触后，尤其在天文与数学等领域产生了较为深远的影响。诚如梁启超所言:“自明徐光启以后,士大夫渐好治天文算学”，而“其于西来法,食而能化,足见民族器量焉”(64)粱启超：《清代学术概论》，上海：复旦大学出版社，1985年，第47页。。不过，这种对外来知识的吸收与融合并非一蹴而就。

由于中西科学知识体系的不同，在当时传入的西学知识中，人们最难以接受的便是三角学。其根源在于中国人的数学思想与实践一贯是代数学的，而不是几何学的。想要用三角学取代传统代数计算方法，就需要人们在概念和工具等多个层面产生思想上的转变。

虽然，一些西方三角学知识在隋唐时期就已经随着佛经从印度传入中国，但并没有产生任何影响。真正意义上的三角学知识及其算表，则是自明末以后通过耶稣会士传入中国。据李俨先生统计，自三角学被引入中国至19世纪末，中国共出版了102部三角学著作，其中关于平面三角学的有39部，球面三角学37部，三角函数表26种。(65)李俨：《三角术和三角函数表的东来》，载《中算史论丛》第3集，北京：科学出版社，1955年，第191页。这些变化可以说，带来了一场数理知识的革命。

《同文算指别编》是最早将西方弦表和三角学知识传入中国的著作，全书内容虽然只有 “截圜弦算”一节，但较为全面地介绍了“弦”“弧”和“全数”等概念，以及“弧”和“弦”的六种用法。书中还通过算例介绍有如何通过弦表进行天文学上的球面三角计算，是一本极具实用性和操作性的三角学手册。本文研究发现，《别编》中的弦表与利玛窦传入的其他西学著作相似，同样也是参照了克拉维斯的著作。不过，《别编》在算例等内容上，因地制宜地做了适当改编，地理纬度选用“京师北极出地四十度”，时间则采用了“万历庚子(1600)”。

此外，由于《别编》属于尚未完成的著作，该书最终并未出版，在当时影响比较有限。到了崇祯改历期间，随着《崇祯历书》的纂修，西方三角学知识通过《大测》《割圆八线表》和《测量全义》等书系统地传入中国。三角八线表的引入和使用，在很大程度上促进了历法改革的进程，许多天文算表得以借此迅速地编算完成。

在改历之初，为了符合中国传统百进制的习惯，在算表编算方面，历局曾计划在翻译西方六十进制表格基础上，另制一份百进制算表，并且通过《通率表》对两种不同的进制单位进行转换计算。然后，由于工作量巨大，且使用不便，历局最后不得不放弃中国传统，转为与西方传统保持一致。此外，做出这样的决定也可能是历局的一项策略，希望以此迫使中法的支持者接受西法。

入清之后，关于三角函数表进制的争论仍旧在延续，这也反映了其传入和会通经历了一个较长的调适过程。在三角函数表受到普遍重视之后，人们也不再仅仅满足于了解其用法，还关注起其不同的构造方法，并且在此基础上亦有所创新。(66)董杰、陈建平：《中国第一部三角学译著<大测>的底本与版本研究》，载《中国科技史杂志》2017年第2期，第51—63页。通过明清之际三角函数表在中国的使用，反映了在欧洲科学知识传入过程中，如何通过消化与吸收近代科学的思维方式、概念，以及工具和方法，逐步不断地调适，以实现对旧有科学范式的改造。

致谢：法国国家图书馆藏《同文算指别编》抄本的调查和整理，起始于作者2012年在巴黎第七大学博士后工作期间参与的HNT(History of Numerical Tables)项目。作者感谢林力娜(Karine Chemla)教授提供《别编》的馆藏信息和线索，以及在2013年5月法国布列塔尼HNT项目Workshop期间帮助获得Christopher Clavius的部分拉丁文著作。