磁致伸缩位移传感器反射波电压特性与阻尼参数优化
2021-06-09张耀松任雷浩
孙 英 张耀松 陈 铮 任雷浩 郑 岩
(1.河北工业大学省部共建电工装备可靠性与智能化国家重点实验室,天津 300130;2.河北工业大学河北省电磁场与电器可靠性重点实验室,天津 300130; 3.中国人民解放军95939部队,沧州 061022)
0 引言
磁致伸缩材料中的铁镓合金在低磁场下能够产生较大的磁致伸缩应变,同时具有应力灵敏度高、抗拉能力强、材料成本较低和易于制备等优点[1-3],因此广泛应用于传感器、换能器、制动器、机器人等领域[4-12]。
磁致伸缩位移传感器以线圈为检测装置,其输出量为电压信号。文献[13]构建了螺旋磁场作用下磁致伸缩位移传感器的输出电压模型。文献[14]对应力波在波导丝中的衰减特性进行研究,提出衰减系数测试方法。文献[15]研究发现,波导丝的磁致伸缩是影响魏德曼效应的重要因素。文献[16]在文献[15]的基础上,基于魏德曼效应得到了含有磁致伸缩系数的输出电压模型,建立了磁致伸缩与输出电压的函数关系。以上研究主要集中在构建输出电压模型和扭转波衰减特性等方面。在提高磁致伸缩位移传感器稳定性和测量准确性、降低干扰信号,尤其是反射波信号对输出电压有效信号的影响等方面研究较少。
在提高传感器精度方面,文献[17]设计了一种移动线圈式传感器结构,提高了检测电压幅值和测量精度,同时传感器信噪比也得到了提高。文献[18]通过调整传统Fe-Ga磁致伸缩位移传感器驱动脉冲电流输入端位置,降低了驱动脉冲电流噪声,提高了输出电压信噪比,同时减小了位移测量误差。在反射波信号影响有效信号提取方面,文献[19]在传统磁致伸缩位移传感器结构基础上,提出一种基于无阻尼扭转波干涉的位移测量方法,增大了检测信号的输出幅值,降低了反射波对测量精度的影响,提高了检测线圈输出的电压幅值、信噪比和位移分辨率。文献[20-21]对传感器检测信号滤波电路进行了改进,提高了传感器的信噪比。以上研究主要通过优化磁致伸缩位移传感器滤波电路和改进测量方法,来提高位移传感器的稳定性和测量准确性。而关于反射波信号会对传感器造成干扰,从而影响传感器工作稳定性和测量准确性方面的研究却鲜有报道。
本文基于材料力学分析波导丝所受摩擦力对应力波传播的影响,阐述阻尼与波导丝之间的摩擦力来源及其与阻尼参数之间的关系,进而推导不同阻尼直径、长度和邵氏硬度等参数下的磁致伸缩位移传感器反射波电压模型。基于该模型得到阻尼参数与反射波电压之间的关系,通过对该模型的分析计算确定阻尼参数的最优范围,通过实验对不同阻尼参数作用下的反射波电压幅值变化进行对比。
1 基本结构与工作原理
磁致伸缩位移传感器基本结构如图1所示。
当位移传感器工作时,脉冲驱动电流产生的环形激励磁场与活动永磁体产生的轴向偏置磁场叠加形成螺旋磁场。由魏德曼效应可知,在螺旋磁场的作用下,波导丝会发生形变产生扭转应力波,应力波以一定的速度向波导丝两端进行传播。当扭转应力波传播到检测线圈时,由于磁致伸缩的逆效应,扭转波信号将会导致波导丝内部的磁通发生改变,被检测线圈检测。根据法拉第电磁感应定律,检测电压可表示为
(1)
式中N——检测线圈匝数
S——检测线圈单匝面积
φ——穿过线圈磁通量
B——磁感应强度t——时间
2 阻尼对传感器反射波电压的影响分析
2.1 反射波信号的产生
由图2可知,当脉冲电流产生的环形激励磁场传播到永磁体处时,将与永磁体产生的轴向磁场相叠加产生螺旋磁场。此时波导丝会产生扭转应力波,该应力波由永磁体处向波导丝两端传播,当应力波传播到固定端时,应力波会在两端都发生反射,发生反射后被检测线圈检测到形成反射波。由于传感器左右两端产生的反射波信号的过程相同,本文重点分析右端产生的反射及其造成的反射波电压。
图3为传感器有效信号与右侧所产生的反射波信号的波形图。从图3可以看出,当反射波信号幅值大于所设置的阈值电压时,反射波信号会被识别为有效信号造成误检测,影响磁致伸缩位移传感器工作的稳定性和测量准确性。
2.2 阻尼作用下传感器反射波电压模型
在磁致伸缩位移传感器中,螺旋磁场由激励磁场与偏置磁场两部分叠加而成,波导丝在螺旋磁场作用下产生应力波,螺旋磁场作用下磁致伸缩位移传感器的输出电压e1表达式为[13]
(2)
式中Hi(R)——波导丝表面处的激励磁场强度
Hm——偏置磁场强度
φm——波导丝中的轴向磁通量
λ——波导丝角应变引起的磁场变化率
L——波导丝长度
r——波导丝半径
μr——波导丝相对磁导率
E——波导丝弹性模量
ν——泊松比ρ——密度
Ia——波导丝截面极惯性矩
传感器量程不大时,可以忽略应力波在波导丝中的自然衰减[22],应力波从永磁体处产生并在波导丝中传播。当没有阻尼作用时,传感器输出电压在波导丝上各个位置相同均为e1;当阻尼作用在波导丝上时,应力波在阻尼作用下会发生衰减,导致传感器的输出电压减小。
设经过阻尼后的输出电压减小量为Δe,不考虑固定端的反射衰减,根据反射波的产生机理可知,传播到检测线圈得到传感器反射波电压e2,可表示为
e2=e1-2Δe
(3)
根据电磁感应定律,阻尼作用下传感器输出电压减小量Δe可表示为
(4)
当检测线圈开路时,线圈中不存在感应电流,线圈自身不会产生磁场,线圈中磁感应强度B的变化来源于波导丝在机械应力作用下的磁感应强度变化,则检测线圈中磁感应强度B可表示为[13]
(5)
式中 dφ/dx——波导丝角应变
将波导丝等效为圆截面直杆,则波导丝角应变dφ/dx与其扭矩T的关系可表示为[23]
(6)
磁致伸缩位移传感器中阻尼通常采用橡胶等粘弹性材料,阻尼对应力波具有衰减作用,该作用来源于波导丝在扭转形变时与阻尼材料发生的摩擦。
由于摩擦作用发生在波导丝与阻尼的接触面,利用微元法对波导丝表面的受力情况进行分析,如图4所示。
由于波导丝直接穿过阻尼,根据粘弹性阻尼材料的回弹作用,波导丝表面质元会受到弹性压力P和摩擦力FΔf的作用,两参数之间的关系可表示为
FΔf=-μkP
(7)
式中μk——阻尼与波导丝之间的摩擦因数
式(7)中的负号表示摩擦力FΔf的方向与波导丝的扭转方向相反。由式(7)可知,摩擦力FΔf和阻尼及波导丝之间的弹性压力P密切相关,而阻尼参数的变化会影响弹性压力,进而导致摩擦力的改变。
阻尼与波导丝之间的弹性压力P是由于波导丝穿过阻尼使阻尼发生形变所产生的。根据橡胶阻尼形变压力计算公式[24]可知弹性压力P是关于变量高度h的连续函数,其表达式为
(8)
其中
S1=2πrld/(2πRld)=r/RG=0.117e0.03Y
式中ld——阻尼长度
d——阻尼直径
H——阻尼受到压缩变化后的等效直径
Eah——阻尼表观弹性模量
i——阻尼几何形状影响系数
S1——阻尼承载面积与自由面积之比,即波导丝和阻尼作用部分面积与阻尼表面积之比
R——阻尼半径
G——阻尼切变模量
Y——阻尼材料邵氏硬度
从式(8)可以看出,弹性压力与阻尼长度、直径和邵氏硬度等参数密切相关。
波导丝表面质元在摩擦力FΔf作用下扭矩TΔf可表示为
TΔf=-FΔfr
(9)
根据合力矩定律,处于该阻尼作用下的波导丝的扭矩为各质元所受分力矩之和,由于摩擦力FΔf作用于波导丝表面,阻尼作用下波导丝的合扭矩Tf可通过曲面积分表示为
(10)
将式(8)、(9)代入式(10)可得到合扭矩Tf为
(11)
将式(6)中扭矩T替换为阻尼作用下波导丝的合扭矩Tf,然后将式(11)、(6)、(5)代入式(4)可得到阻尼作用下传感器输出电压减小量Δe为
(12)
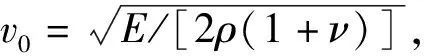
(13)
将式(13)代入式(12)得到
(14)
将式(14)、(2)代入式(3)得到阻尼作用下反射波电压e2表达式为
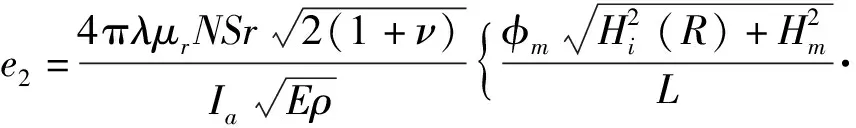
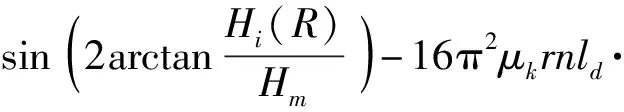
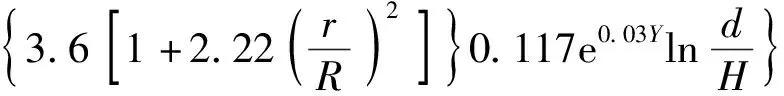
(15)
对比式(15)与式(2)可以发现,相比于传感器有效信号输出电压e1,在阻尼作用下传感器反射波电压e2中含有阻尼参数A,其表达式为
(16)
该式中,包含波导丝之间的摩擦因数μk、波导丝半径r、阻尼半径R、阻尼长度ld、比例系数n、邵氏硬度Y等参数。
当确定了磁场、波导丝材料、检测线圈结构以及阻尼与波导丝之间的摩擦因数后,磁致伸缩位移传感器反射波电压主要取决于阻尼长度、直径及邵氏硬度等参数。分析阻尼参数对反射波电压的影响,并通过实验进行验证,选取合适的阻尼,使得反射波电压远远小于输出电压有效信号,最大程度上降低反射波信号对有效信号提取造成的影响。
3 反射波电压计算
利用式(15)计算传感器反射波电压。波导丝选用性能较好的Fe-Ga波导丝,由文献[13]可知,偏置磁场与脉冲激励磁场相同时能够产生较大的输出电压。因此,本文选择偏置磁场和激励磁场均为5 kA/m,两磁场作用能够产生磁场强度为7 kA/m的螺旋磁场,此时磁致伸缩位移传感器可以产生较大的有效信号。其他计算参数[13]如表1所示。
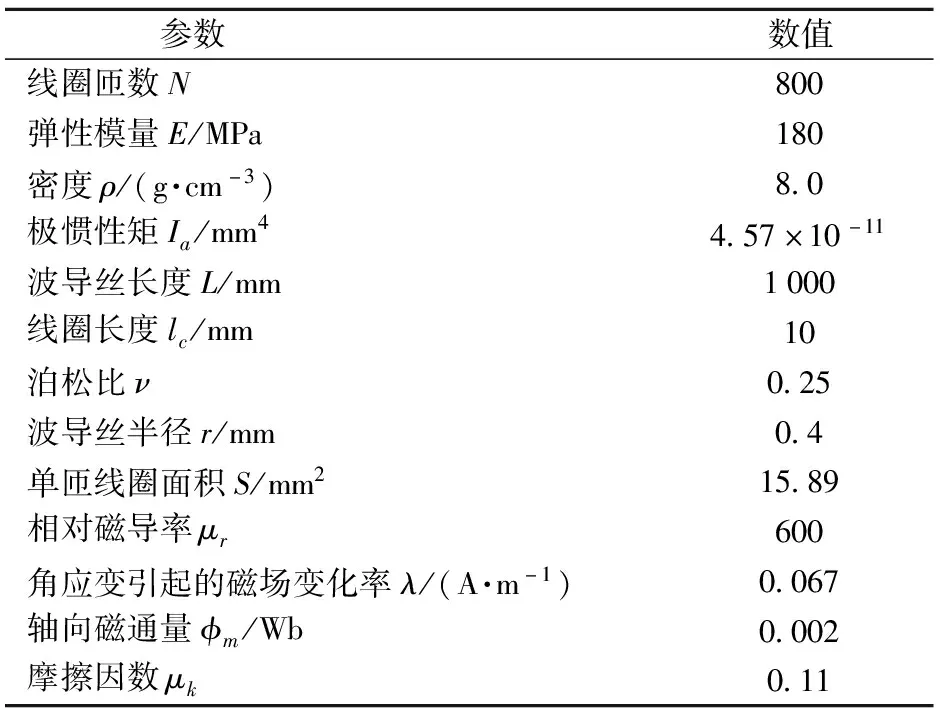
表1 计算参数
由式(15)可知,阻尼参数中阻尼长度、直径和邵氏硬度等参数都会对反射波电压幅值造成影响。从式(16)可以看出,在阻尼参数A表达式中,阻尼长度、直径及邵氏硬度三者分别与阻尼参数A呈正比关系。经过分析计算发现阻尼直径从10 mm变为5 mm时ln(d/H)的值变化了0.03,说明阻尼直径的变化对阻尼参数A的影响很小,因此本文选择与塑料套管的内径相同、直径为10 mm的阻尼,进而分析该直径下阻尼长度和邵氏硬度的变化对反射波电压幅值的影响。
3.1 阻尼长度与反射波电压的关系
邵氏硬度为25、30、35下阻尼长度与反射波电压之间的关系如图5所示。
由图5可看出,在邵氏硬度为25、30、35时,随着阻尼长度的增加反射波电压幅值的变化情况基本相同,均随着阻尼长度的增加逐渐减小。当阻尼长度超过4 mm后,反射波电压幅值下降幅度增大。当反射波电压为零时,邵氏硬度为25所对应的阻尼长度为16.6 mm;邵氏硬度为30所对应的阻尼长度为15.2 mm;邵氏硬度为35所对应的阻尼长度为14.2 mm。
3.2 阻尼邵氏硬度与反射波电压的关系
选取了阻尼长度分别为5、10、15、20 mm的阻尼,分析了各个长度下阻尼邵氏硬度与反射波输出电压之间的关系,如图6所示。
由图6可看出,在阻尼长度为5、10、15、20 mm的情况下,随着阻尼邵氏硬度的增加反射波电压幅值变化趋势基本相同,均随着邵氏硬度的增加反射波电压幅值逐渐减小,并且随着长度的增大,反射波电压幅值的变化幅度增大。还可以看出,当反射波电压为零时,长度为5 mm的阻尼邵氏硬度为78;长度为10 mm的阻尼邵氏硬度为58;长度为15 mm的阻尼邵氏硬度为33;长度为20 mm的阻尼邵氏硬度为12。
由图5、6可得,阻尼长度和邵氏硬度的变化都对反射波电压的幅值产生影响,阻尼长度和邵氏硬度的增大,均会使反射波电压幅值降低。分析反射波信号产生的原因及阻尼参数与反射波电压之间的关系,可以根据实际情况选择最佳的阻尼参数,使其能够大大降低反射波电压幅值。反射波电压幅值越小,反射波电压对有效信号提取的影响就越小。
4 实验与结果分析
4.1 实验平台搭建
实验测试平台[9]如图7所示。实验选用直径为0.8 mm、长度为1 m的铁镓丝,并将其固定在内径为10 mm、外径为12 mm的铁氟龙塑料管内,铁镓丝末端采用橡胶阻尼固定,然后再将其放入内径为13 mm、外径为15 mm、壁厚为2.5 mm的316L的不锈钢探杆中。实验中使用的电源为稳压电源,能够为后续信号调理电路提供稳定的工作电压。信号发生器采用TFG6092A型,脉冲频率设定为1 000 Hz,宽度为7 μs,高电平为5 V。检测线圈采用直径0.06 mm的铜漆包线绕制而成,其长度为10 mm,平均半径为2 mm,匝数为800匝。检测线圈套在波导丝的头部用于接收信号,信号显示采用DPO3014型四通道示波器,显示输出的电压信号。
4.2 阻尼长度对反射波电压的影响
实验对半径为10 mm和邵氏硬度分别为25、30、35的阻尼进行研究,分析不同阻尼长度作用下的传感器反射波电压变化情况,如图8所示。
从图8可以看出,在3种不同阻尼邵氏硬度下,反射波电压幅值均随着阻尼长度的增大而逐渐减小,其变化趋势基本相同。邵氏硬度越大,反射波降为零所需要的阻尼长度越短。邵氏硬度为25、阻尼长度为16 mm时反射波电压幅值降低为零;邵氏硬度为30、阻尼长度为14.8 mm时,反射波电压幅值降低为零;邵氏硬度为35、阻尼长度为13.7 mm时反射波电压幅值降低为零。
4.3 邵氏硬度对反射波电压的影响
实验对半径为10 mm和长度分别为5、10、15、20 mm的阻尼进行研究,记录了不同邵氏硬度的阻尼作用下反射波电压幅值的变化情况,如图9所示。
从图9可以看出,在不同阻尼长度下,反射波电压幅值随着邵氏硬度的增大而逐渐减小,且阻尼长度越长,反射波幅值随阻尼邵氏硬度的增大变化的幅度也越大。阻尼长度越长,使得反射波电压幅值降为零所需的邵氏硬度越小。阻尼长度为5 mm、邵氏硬度为74时反射波电压幅值降为零;长度为10 mm的阻尼在邵氏硬度为56时反射波电压降为零;阻尼长度为15 mm、邵氏硬度为31时反射波电压幅值降为零;阻尼长度为20 mm、邵氏硬度为10时反射波电压降为零。反射波电压幅值越小,反射波电压对有效信号提取的影响越低。
实验发现,当阻尼长度小于5 mm时,其对应的邵氏硬度大于80,此时阻尼类似于固定端,在阻尼作用处会有新的反射波干扰出现。因此在对阻尼进行选择时,应避免阻尼长度过短和邵氏硬度过大。
4.4 阻尼实验误差分析
从图5、8和图6、9可以看出阻尼长度和邵氏硬度变化对反射波电压的影响,实验分析与理论计算中的反射波电压幅值变化情况基本相同。实验结果与理论计算对比如表2所示。当反射波电压幅值为零时,阻尼长度与邵氏硬度存在一些误差,实验数据比理论计算值均偏小。阻尼长度和邵氏硬度变化的误差主要是由扭转应力波在波导丝中传播时衰减以及应力波在末端经过反射产生的衰减造成。
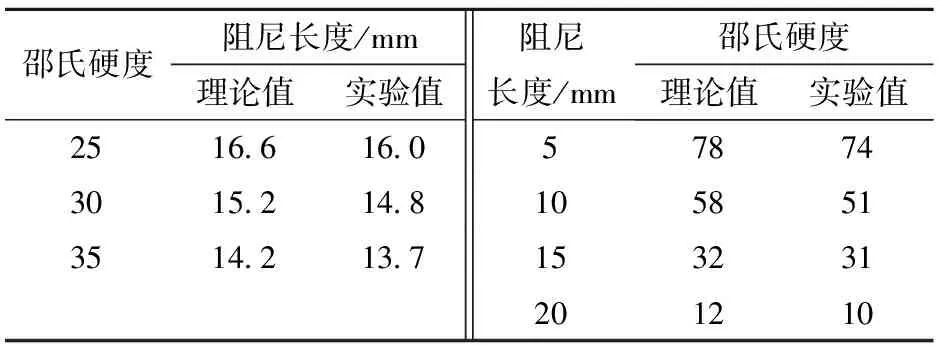
表2 理论结果与实验结果对比
4.5 阻尼参数选择
在实际情况下由于电磁干扰等噪声信号的存在,一般电压在5 mV以下都不在提取范围[14]。从理论计算与实验分析中发现,为使反射波电压幅值降为5 mV以下,在阻尼直径为10 mm的情况下,阻尼长度和邵氏硬度的取值可以为:长度5 mm、邵氏硬度75;长度10 mm、邵氏硬度50;长度15 mm、邵氏硬度30;长度20 mm、邵氏硬度15等。
考虑到阻尼长度对位移传感器量程的影响,在能够使得反射波电压不影响有效信号的情况下,阻尼长度应越短越好。当阻尼长度小于5 mm时,此时邵氏硬度较大,会有新的干扰产生。因此给出了阻尼长度取值范围为5~10 mm,邵氏硬度取值范围为50~75。
利用实验室所搭建的平台对不同阻尼参数作用下反射波电压幅值变化进行比较,得到的输出电压波形如图10所示。从图10可以看出,在无阻尼时反射波电压幅值约为75 mV;在直径为10 mm时,长度10mm和邵氏硬度20、长度15 mm和邵氏硬度20、长度10 mm和邵氏硬度40、长度10 mm和邵氏硬度50的阻尼作用下反射波电压幅值分别约为50、37、18、4 mV;在所选最优阻尼(直径10 mm、长度10 mm、邵氏硬度50)作用下有效信号电压约为100 mV并保持不变,反射波电压幅值从75 mV降至4 mV左右,约为原来的1/15,远小于传感器有效电压信号,不会对传感器造成干扰。
5 结论
(1)基于磁致伸缩位移传感器输出电压模型及阻尼对应力波的吸收衰减作用,构建了阻尼作用下磁致伸缩位移传感器反射波电压模型,获得阻尼参数与反射波电压之间的关系。通过理论分析与实验验证发现,阻尼参数对反射波电压幅值有很大影响,随着阻尼长度和邵氏硬度的增加,反射波电压幅值逐渐减小。
(2)考虑到阻尼长度对传感器量程影响及阻尼长度较短、邵氏硬度较大带来的干扰等因素,确定了阻尼长度取值范围为5~10 mm、邵氏硬度取值范围为50~75,通过实验对不同阻尼参数作用下的反射波电压幅值变化进行比较。在长度为10 mm、直径10 mm和邵氏硬度为50的最优阻尼作用下反射波电压幅值从75 mV降至4 mV左右,对反射波电压起到了很好的抑制作用,基本消除了反射波对有效信号提取造成的影响,提高了传感器的稳定性与测量准确性。
