核心素养视域下《分数的意义》教学例谈

向子龙 谭健

如何帮助学生深入理解分数的由来及意义，正确把握分数的本质呢？笔者以谭健老师执教的人教版数学五年级下册《分数的意义》为例，谈核心素养视域下如何引导学生触摸分数概念的本质。

一、渗透史料，回归概念本质

课始，教师利用微课展示分数的发展史，引导学生了解分数产生的背景和过程。随后，教师展示“分数的产生”情境图。第一幅图表现了古人度量物体长度时遇到的困惑——剩下的不足一段怎么记录。这个情境形象地揭示了在测量物体时，由于得不到整数的结果，而产生了把一个单位等分成若干份再测量的需要。另一幅图给出了两个小朋友分一个西红柿、一块月饼和一包饼干的情境，通过分的实例，使学生初步感悟：利用分数可以解决整数除法除不尽的问题，即从数学内部发展的角度，揭示了分数的来源。教师通过展示、分析“测量”与“分物体”的实例，唤起学生的已有经验，使学生感悟分数是适应客观需要而产生的、源于生活的数，分数可以表示一个具体的量，并潜移默化地使学生了解相关数学史。这样教学，能使学生在数学文化背景下开展思维活动，获得素养提升。

二、自主探究，深化概念理解

“单位‘1”和“分数单位”是理解分数的意义的两个关键概念。

1.多元表征，理解单位“1”

传统的《分数的意义》教学，教师往往会先提出“生活中哪些物体可以用1来表示”“自然数1除了可以表示一个物体，还能表示什么”等问题，再指出“自然数1除了可以表示1个物体，还可以表示许多物体组成的一个整体”，进而揭示单位“1”。这样的教学仅仅停留在“告诉”的层面，其教学过程本质上是接受式的。那么，如何引导学生更好地认识单位“1”呢？

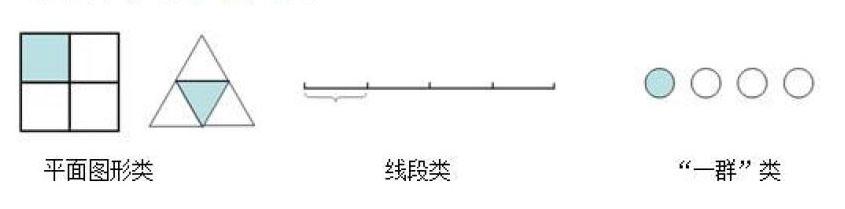
教学中，教师首先引导学生利用手中的小纸片，通过折一折、画一画、涂一涂等方法表示[14]。学生独立思考后，在小组内交流，再全班汇报展示，形成三类成果（如下图）。

教师首先以“平面图形类”和“线段类”成果为例，引导学生思考“为什么不同的图形都可以表示[14]”，并归纳得出“把一个图形平均分成4份，这样的1份可以用[14]来表示”。第三类图能不能用[14]表示呢？这个问题引发了学生的思辨。学生讨论得出：把4个圆形看成一个整体，把这个整体平均分成4份，其中的1份也可以用[14]来表示;用这幅图表示[14]，与之前用一个图形表示[14]的区别在于要分的总数不同。教师顺势引导：“如果有更多的圆，怎么表示[14]，你能画一画吗？”学生形成如下作品。

教师追问：“为什么数量不同，却都能表示[14]？”师生共同归纳得出：第一幅图是4个圆的[14]，第二幅图是8个圆的[14]，第三幅图是12个圆的[14]，这里的[14]所表示的圆的个数不同，是因为整体的数量不同。

接下来的教学中，教师围绕[14]的多元表征，揭示单位“1”。

师（白板呈现图）：你能在每一幅图上表示出它的[14]吗？

生1：把4根香蕉看作一个整体，1根香蕉是这个整体的[14]。

生2：把8 个面包看作一个整体，平均分成4份，每份的2个面包是这个整体的[14]。

师：同学们在表示[14]的过程中，有什么发现？

生3：都是把物体平均分成4份，表示这样的1份。

生4：我发现有的是把1个图形平均分，有的是把1把香蕉、8个面包平均分。

师：一个图形称为一个物体，那么4根香蕉、8个面包是由许多单个物体组成的，我们称作一些物体。不论是一个物体，还是一些物体，都可以看作一个整体。一个整体可以用自然数1来表示，我们通常把它叫作单位“1”。对于这个整体，你还能想出其他的例子吗？动脑筋创造几个分数。

谭老师跳出传统教学方式，为学生创设实践性问题情境，提供充分的感性材料，使学生在动手操作、独立思考、观察讨论、合作交流等自主探究的过程中理解分数的意义，培养了学生分析、比较、概括等逻辑思维能力。以上设计，让学生对一个整体的概念有了正确的理解，拓展了学生对“[14]”和单位“1”的认识。

2.充分体验，理解分数单位

教师用白板呈现教科书第46页做一做：把一堆糖块，平均分成2 份、3份、4份……组织学生小组合作完成。学生用小塑料方块表示糖块，动手分一分，并把结果填在“探究卡”上。在汇报环节，教师首先引导学生说明[12]、[23]、[34]分别表示什么意思，接着说一说这些分数的分子和分母分别表示什么意思，然后师生通过交流，总结得出：把单位“1”平均分成若干份，表示这样一份的数就是分数的分数单位。如，[23]的分数单位是[13]。最后，教师带领学生利用磁吸小圆片找分数单位，发现所有分数单位的共同特点是表示“几分之一”。

分数具有多重意义，这意味着教师必须不断激发学生的已有经验，由浅入深、分步扩展，帮助学生主动建构新的分数经验。学生在解决问题的过程中，经历了多次的比较、概括，清晰地认识了分数单位就是分数的计数单位，分子就是计数单位的个数，水到渠成地理解了分数单位的内涵。

三、巩固应用，拓展概念认知

在完善了学生对分数概念和内涵的认知后，教师设计有梯度的练习，引导学生灵活运用知识，解决有关分数的实际问题。

首先，教师用白板設计了“配对游戏”，引导学生通过观察，把分数与相应的图片配对。游戏设计不仅调动了学生的学习兴趣，而且让学生在“拿”的过程中，巩固了对分数意义的理解。其次，教师结合教科书习题，设计了“猜谜语”“动手折一折”的练习，引导学生经历猜想、操作、验证的过程，体会分数的内涵，感受数学与生活的紧密联系。最后，教师设计闯关练习，引导学生在纠错中积累正确表征分数的活动经验。

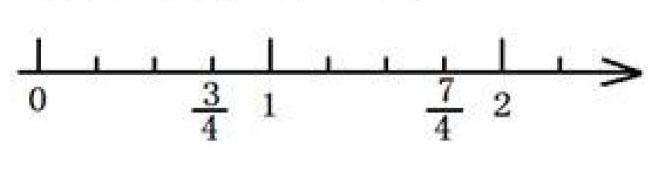
闯关：在下面的数轴上，[34]和[74]之间，只有3个分数。请判断对错并说明理由。

判断为正确的学生反映出其缺乏分数的数感，他们只是把数轴上[34]和[74]之间能看到的、已经标记出来的3个刻度线作为可以找到的分数。此时教师没有揭晓答案，而是提名判断为错的学生上台演示[34]和1之间可以有[78]、[1316]……这样的分数。教师通过进一步地说理，让学生明白“无论哪两个分数之间，都存在无数个分数”，使学生感悟分数的奇妙特征。

（作者单位：向子龙，恩施州巴东县教育教学研究室;谭健，恩施州巴东县大支坪镇中心小学）

助理编辑  刘佳