再探椭圆“虚渐近线”的一个性质

内蒙古巴彦淖尔市第一中学(015000) 杨松松 王东伟

定义[1]把直线y=称为椭圆的虚渐近线.

文献[2]给出如下性质:

性质1如图1,设M是椭圆= 1(a > b >0,b ̸=c) 上任意一点,过点M作椭圆两虚渐近线的垂线,垂足为G、H,分别与另一条渐近线相交于P、Q点,则为定值.

图1

笔者受到文献[2]的启发,对以上性质进行了再探究,于是得出:

命题1如图2,已知M为平面直角坐标系xOy内一点,直线l1,l2的斜率分别为k1,k2(其中,k1̸=k2,且k1,k2至多有一个为零),过点M分别作l1,l2的垂线,垂足分别为G、H,若直线MG与l2交于点P,直线MH与l1交于点Q,则为定值.

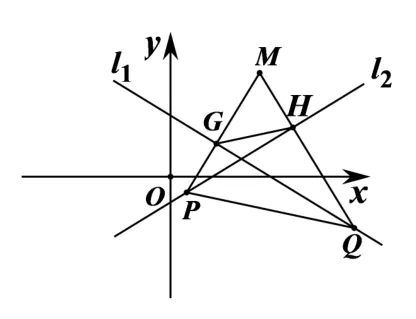
图2

证明设k2̸= 0,由MH⊥l2得kMH · k2=−1,于是kMH=由到角公式得:|tan ∠MQG|=于是

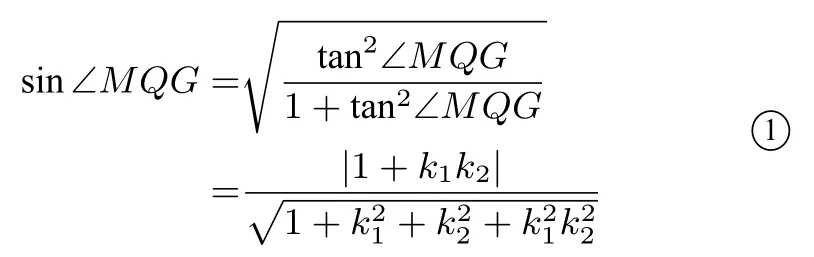
由MG⊥QG,MH⊥PH得∠MQG=∠MPH,于是

在Rt∆MQG和Rt∆MPH中,

由①②③④及∠GMH=∠PMQ可得

令M为椭圆= 1 上一点,取l1:y=l2:y=因此k1==即为性质1 的结论,因此性质1 是命题1 的特例.

在命题1 的条件下,若直线l1,l2的倾斜角分别为α,β,则由⑤得:

命题2已知M为平面直角坐标系xOy内一点,直线l1,l2的倾斜角分别为α,β(其中,α ̸=β,且|α−β|̸=),过点M分别作l1,l2的垂线,垂足分别为G,H,若直线MG与l2交于点P,直线MH与l1交于点Q,则=cos2(α−β).