一道质检导数压轴题的探究

福建省福清华侨中学 (350300) 王 莺

福建省福清三山中学 (350318) 林永光

试题再现：已知f(x)=ex，g(x)=x+alnx.

(1)讨论g(x)的单调性；

本文拟从试题的命题立意、试题溯源、解法探析、试题延伸等方面对该试题进行研讨.

1 命题立意

本题考查直线与曲线相切，利用导数研究函数的单调性、极值与最值、不等式的证明，考查逻辑思维能力、运算求解能力、转化化归能力，体现了逻辑推理、数学运算等核心素养.试题较难.

2 试题溯源

曲线的公切线问题，在高考中也曾出现过，如2016年全国卷Ⅱ理科数学第16题：若直线y=kx+b是曲线y=lnx+2的切线，也是曲线y=ln(x+1)的切线，则b=.

两道试题不同之处在于，上面这道真题中两个切点横坐标均可具体求出，篇首试题中x1,x2均无法求出来，且消元后的表达式较为复杂.

3 解法探析

求解两曲线的公切线问题，通常采用的“先分后合”的方法，通过假设两个切点，分别算出切线方程，再由斜率及y轴上的截距相等，得到关于两个切点横坐标的方程组，消元，求解出某个切点横坐标，问题得解.

求解本题难点有两个.其一：得到方程组之后，消元后的式子较为复杂，难以继续下去；其二：x2的取值范围与x1相关联，变量x1,x2相互纠缠在一起，令学生望而生畏.

命题组给出(2)的求解思路如下.

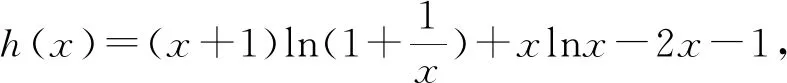
解法一将x1表示为x2的函数，通过研究h(x)的单调性、最值，对x1的取值进行限定，解题过程中用到了“虚设零点”这一方法，整个过程构思巧妙.但对于大部分学生，较难想到用x2来表示x1，更难想到通过限定x1的取值，以确定x2的下界.解法二较常规，通过消元，将问题转化为研究h(x)零点的范围，学生容易想到，但由于h(x)的形式较为复杂，大部分学生未必有能力对h(x)进行求导.

事实上，解法二中求解h(x)零点x2的范围，除了直接求导之外，常见的还可以将h(x)一分为二，通过研究两个函数的交点位置，定出x2的范围.遵循这样的思路，笔者得到了如下解法.

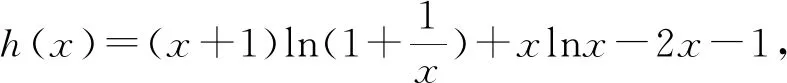
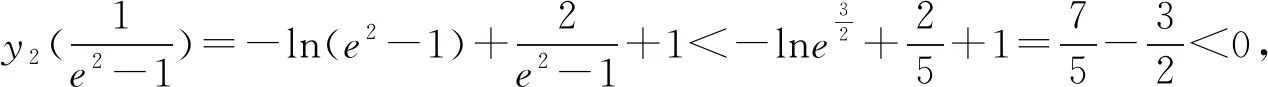
4 试题延伸

图1

5 教学感悟

我们常说，教学应以学生为主体，那么如何在教学中体现学生的主体地位？笔者认为教师最基本应该做到“设身处地”——站在学生的视角去思考问题.在教学中，教师要时刻进行如下评估：所创设的问题是否在学生的最近发展区，让学生能够跳一跳摘到“桃子”？所采用的的方法是否是学生熟悉的，让学生能够结合自己的认知对新知识进行建构？对解法是否进行了优化，以帮助学生更好的理解掌握？是否引导学生对解题过程进行归纳总结，以助力学生解题质量的提升？如果答案都是肯定的，那么，学生学习之“慧根”将会得到很好的启迪，解题活动之“道术”将会得到很好的展现.