一道四边形面积最大值问题的探究
2021-06-07江苏省无锡市第六高级中学214000
江苏省无锡市第六高级中学 (214000) 谢 吉
本文拟通过对一道四边形面积最大值问题的深入研究,旨在帮助同学们拓宽处理此类问题的常用解题思维,巩固所学数学知识、方法在解题中的灵活运用能力;同时也指出教材例、习题的典型性可进一步挖掘,以及强化变式训练的重要性.
考题呈现(2020届西安高级中学高三模拟题)在平面四边形ABCD中,AB=BC,∠ABC=60°,CD=2,AD=4,则四边形ABCD的面积的最大值为.
试题分析:本题符合新课标“注重在知识网络的交汇点处设计试题,对数学基础知识的考查达到必要的深度”的高考理念,主要考查学生对相关数学知识的灵活、综合运用能力,提升考生的数学核心素养.本题亮点体现在两个方面:一是考查学生的数形结合能力以及推理论证能力;二是如何巧妙借助“消元”技巧,或转化思想加以灵活分析,培养学生分析问题、解决问题的能力.
解法探究:因为AB=BC,∠ABC=60°,所以△ABC是等边三角形.如图1所示,为了便于进行分析、叙述,先画出对应的图形,并设等边△ABC的边长为x.

图1

评注:此解法的关键是借助“设元”技巧,先根据解三角形知识构建等量关系,再根据同角三角函数中的平方关系实施“消元”变形,进而转化为二次方程的“根”的存在性问题.
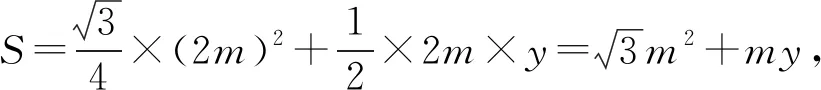
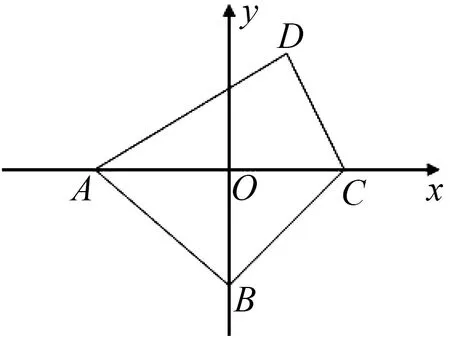
图2
评注:上述解题思路可概括为,先根据图形的特殊性,适当建立平面直角坐标系;再通过设出相关点的坐标,构建等量关系,并活用“消元”技巧获得关于“m2”的一元二次方程;最后根据二次方程有实数根,构建不等式加以灵活求解.
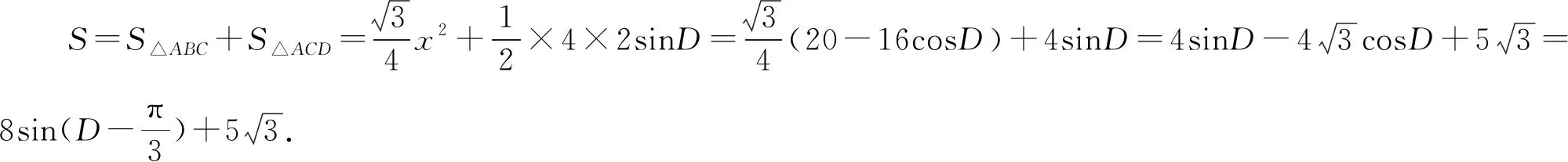


考题探源:本题源于北师大版教材必修五第55页例3(具体展示如下),所以该题“源于教材,高于教材”设计较好.
如图3所示,已知⊙O的半径是1,点C在直径AB的延长线上,BC=1,点P是⊙O上半圆上的一个动点,以PC为边作等边三角形PCD,且点D与圆心分别在PC的两侧.(1)若∠POB=θ,试将四边形OPDC的面积y表示成θ的函数;(2)求四边形面积的最大值.
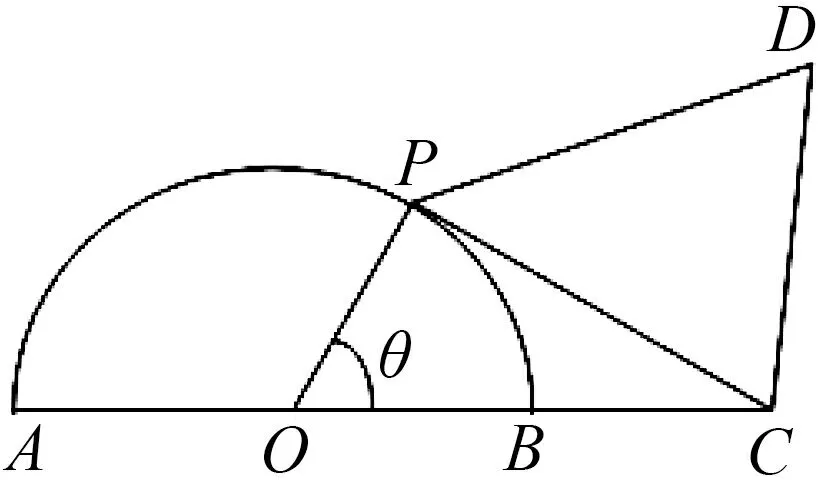
图3
变式训练(原创)如图4,已知平面四边形ABCD,连接AC,其中∠ACB=60°,且AB⊥BC,AD=1,CD=2,则四边形ABCD的面积的最大值是.

图4
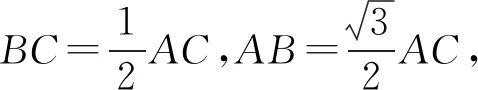
综上可见,求解四边形面积最大值时,从数学思想方法看,需关注“数形结合思想”、“转化与化归思想”的综合运用;从解题技巧看,需关注“设元”、“消元”技巧的灵活运用;从求最值角度看,需利用函数的单调性、基本不等式、三角函数的性质等灵活求解.一言以蔽之,此类问题有利于强化解三角形与其他知识在解题中的综合运用能力,有利于优化学生的认知结构,培养学生的探究精神以及创新意识.
