对2020年全国Ⅰ卷导数压轴题的错解探源*

江西省南昌县莲塘第一中学 (330200) 李树森 李艺璇

2020年全国高考数学Ⅰ卷理科21题函数与导数压轴题，该试题重视数学本质，突出理性思维和对关键能力的考查．此题是一道以不等式恒成立为背景，具有高度的迷惑性、解题具有一定创新性的试题，本文从此题的第2问的一个典型的错误探究其错误的根源，并从多视角探究其解法.

1 试题呈现

例1 已知函数f(x)=ex+ax2-x.

(1)当a=1时，讨论f(x)的单调性；

本题以不等式恒成立问题为背景，考查利用导数研究函数的单调性，极值，求参数取值范围等导数中的热点问题,突出对数学抽象、数学运算、逻辑推理等核心素养的考查.对于已知恒成立问题求参数的取值范围，是常考题型.初看本题第2问的不等式是在区间的端点取等号，很多学生容易和所谓的“端点效应”相联系而导致错误，本题除了在端点取等号同时又在区间的某点处取等号，因此学生解答此题盲目套用模型解题. 本题常用的解题策略是分离参数法，但是运算量大，让一部分考生望而却步.若在不等式的构造上做出理性分析，便可得到更简洁的解题方法.该题体现了对数学核心素养以及化归与转化思想的考查，是一道具有选拔功能的好题.

2 错解探源

这是一种很常见的错误解法，笔者将通过以下两个案例帮助探究此类问题何时适用“端点效应”，以及“端点效应”在该题当中失效的根本原因.

案例1 (2017年全国Ⅱ卷文科21题节选)设函数f(x)=(1-x2)ex，当x≥0时，f(x)≤ax+1，求a的取值范围.

解析：由f(x)≤ax+1得(1-x2)ex-ax-1≤0，设g(x)=(1-x2)ex-ax-1，注意到g(0)=0，g′(x)=(1-2x-x2)ex-a，g″(x)=(-x2-4x-1)·ex<0，则g′(x)在[0,+∞)上为减函数，g′(0)=1-a≤0，则a≥1，当x≥0，g′(x)≤0，即g(x)在[0,+∞)上为减函数，所以g(x)≤g(0)=0

当a<1时，则存在x0∈(0,+∞)，使得g′(x)=0，又因为g′(x)在[0,+∞)上为减函数，所以当x∈(0,x0)时，g′(x)>0，即g(x)在(0,x0)上为增函数，所以当x∈(0,x0)，则有g(x)>g(0)=0与条件相矛盾，所以a≥1.

案例2 (2010年全国Ⅰ卷理科21题节选)f(x)=ex-1-x-ax2，当x≥0时f(x)≥0，求a的取值范围.

上述两个案例的共同特征是：对于任意的x∈[m,+∞)不等式f(x)≥0恒成立，且f(m)=0，当f(n-1)(m)=0，则需要满足f(n)(m)≥0，利用f(n)(m)≥0求出的参数的范围为不等式成立的一个必要条件，但若并且n阶导函数为单调增函数，此范围刚好也满足了其充分性，只需要说明其范围的补集并不符合条件.所以，确实存在一些问题符合所谓的“端点效应”，通过该方法问题在一定程度上得以简化，但同时也会固化思维，而更容易犯错.我们不妨利用上述方法求出的参数范围，将其作为不等式成立的必要条件，以此缩小讨论的范围.

3 正解探究

视角1 分离参数法，将不等式的恒成立问题转化为最值问题处理.

视角2 将原函数适度变形为指数型函数与多项式函数的乘积形式，通过分类讨论求出函数最值.

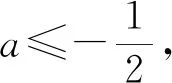
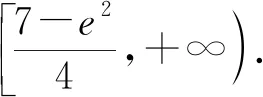
视角3 寻求不等式成立的必要条件，缩小讨论范围，运用充分条件确定参数的范围.

视角4 借助图像的直观性，将不等式的取等条件转换为两曲线的相切的切点来处理，探讨临界状态值，对参数分类讨论，从而确定参数的范围.

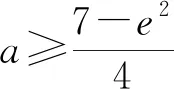
导数压轴试题中的恒成立问题是常考内容，在掌握上述常见四种视角的基础上，要辨别问题类型的本质，解决导数综合问题善于对函数的结构形式进行变式，构造恰当的函数，并借助函数图象直观性，将不等式问题巧妙转化，找到临界位置，善于运用相关结论，掌握解题技巧．通过典型的试题，针对性的训练，逐步提高对此类问题的解决能力．