整体建构以问促教 彰显勾股之美

广东省东莞市企石中学(523500) 武模伟

章建跃博士在数学核心素养的解读中指出: 从数学知识发生发展过程的合理性、学生思维过程的合理性上加强思考,这是落实数学学科核心素养的关键点,要把如何抽象数学对象、如何发现和提出数学问题作为教学的关键任务,以实现学生从“知其然”到“知其所以然”,再到“何以知其所以然”的跨越[1].基于此,笔者将教学内容进行问题化设计,让教学过程具有渐进性、知识结构具有完整性,在学生思维的最近发展区设计环环相扣的问题.

1 内容和内容解析

勾股定理指出了直角三角形三边之间的数量关系,这就搭建了几何图形和数量关系之间的一座桥梁.勾股定理不仅在平面几何中是重要的定理,而且在三角学、解析几何学、微积分中都是理论的基础,对现代数学的发展也产生了重而深远的影响,没有勾股定理,就难以建立起整个数学的大厦.因此,确定本节课的教学内容为勾股定理的探究、证明及简单应用.由此,在直角三角形中,已知任意两边长,就可以求出第三边长.

2 学情分析

学生在学习勾股定理之前已经学习了三角形的相关知识,对几何知识和代数知识有一定的认识,初步掌握了探究图形性质的一般方法.但是学生在自主探索图形性质并运用符号语言证明性质的能力较差,探索意识薄弱,缺乏严谨的逻辑推理能力.尤其是本节课中用到的无字证明推导出勾股定理的方法学生平时接触甚少,因此在教学中需要引导学生自主证明,提高学生的推理能力和分析能力.

3 教学目标

(1)经历探索,验证勾股定理的过程,掌握勾股定理,进一步了解等面积法的应用.

(2)通过不同证明方法的探究,进一步发展空间观念和推理能力,体会数形结合的数学思想.

(3)借助勾股定理丰富的文化背景,培养学生的人文底蕴和科学精神的核心素养.

4 教学重点、难点

重点: 探索并证明勾股定理,利用割补法求面积.

难点: 借助拼图和网格的方式,利用等面积法证明勾股定理,并结合方程思想尝试从不同角度理解、证明勾股定理.

5 教学过程

环节1: 建构三角形的边、角特征

问题1: 前面我们学习了三角形的相关知识,并从相关要素,边、角的角度去研究三角形的性质.对于特殊的三角形,如等腰三角形、等边三角形的边角特征也进行了系统的学习.下面请同学们回答以下几个问题.

(1)如图1,当为ΔABC一般的三角形时,则a、b、c之间有怎样的数量关系?

图1

(2)如图2,等腰三角形两个底角相等,则b、c之间有怎样的数量关系?

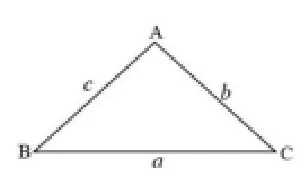
图2

(3)如图3,等边三角形三个角相等,则a、b、c之间有怎样的数量关系?

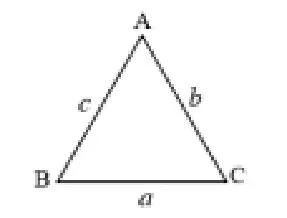
图3

追问1: 直角三角形的角有什么性质?

追问2: 类比等腰三角形、等边三角形的学习过程,对于直角三角形的性质,你认为接下来应该研究什么呢?

教学分析: 从单元整体教学出发,先是复习三角形的相关知识,建构等腰三角形、等边三角形的边角特征.经过探究角的数量关系可以决定三角形的形的特征,由形的特征转化可得到边的数量关系,把形和数密切地联系起来.教师通过提出启发性的问题让学生明确本节课的学习任务.

环节2: 在网格中探究等腰直角三角形的三边关系

看似平淡无奇的现象有时却隐含着深刻的道理.相传2500 多年前,古希腊数学家毕达哥拉斯在朋友家做客时,发现朋友家用地砖铺成的地面图案,就存在这个图形.他通过探究图中三个正方形的面积关系,从而发现了直角三角形的三边满足某种数量关系.

问题2: 请观察地砖图4,我们发现,两个等腰直角三角形可以拼成一个小正方形,而4 个等腰直角三角形可以拼成一个大正方形.若三个正方形分别记为A、B、C,那么它们的面积有什么关系呢?

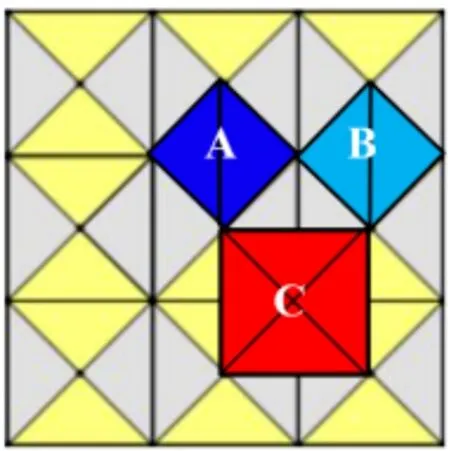
图4

追问: 观察图5,由这三个正方形A、B、C的边长构成的等腰直角三角形的三条边之间有怎样的特殊关系呢?

图5

教学分析: 通过设置问题串,层层递进,再现毕达哥拉斯发现勾股定理的过程.在观察地砖图的过程中发现数形关系图,从数学的角度,先研究图形的面积关系再转化到研究边之间的关系.教师引导学生归纳出“等腰直角三角形两直角边的平方和等于斜边的平方”.但可能会有学生提出不一样的看法,如归纳出“等腰直角三角形的直角边平方和的两倍等于斜边的平方”.

环节3: 在网格中探究一般直角三角形的三边关系

问题3: 那么对于一般的直角三角形,它的三边之间是否也满足这种关系呢? 下面各小组进行探究,在图6 中,请分别以这个直角三角形的各边长为边向三角形外画正方形A、B、C.图中每个小方格的面积均为1.

图6

追问1: 请在画出的图7 中计算,三个正方形的面积分别为多少?

图7

追问2: 三个正方形的面积之间满足怎样的数量关系?

追问3: 通过前面探究活动所得的结果,猜一猜直角三角形的三边之间应该有什么关系?

教学分析: 由于正方形A、B的边长通过数格子可以直接计算,因此较易得到其面积.关键是怎样求出正方形C的面积,学生在小学时已经学习了估算法和拼图法,利用这两种方法可以猜出正方形C的面积.然而数学最讲究逻辑的严谨性和结论的准确无误,一就是一,二就是二,因此启发学生需要寻求新的方法计算其精确值,于是割补法的出现就显得顺其自然了.在此过程中渗透从特殊到一般的数学思想,为学生提供参与数学活动的时间和空间,发挥学生的主体作用,培养学生的类比迁移能力及探索问题的能力,使学生在相互欣赏、争辩、互助中得到提高.在网格背景下,通过观察分析三个正方形的面积关系归纳得出一般直角三角形的三边关系,为形成猜想提供了典型特例,猜想的形成变得水到渠成.

环节4: 证明勾股定理

问题4: 我们猜想: 如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2.那么在去掉格点的情况下,怎么计算正方形的面积呢?

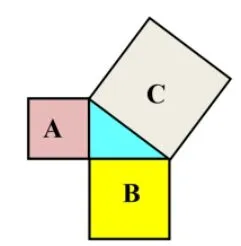
图8

追问1: 在图9 中,四个直角三角形为什么全等,你能证明吗?

图9

追问2: 除了图9 的“补法”,你还有其他的方法吗?

追问3: 根据“补”法,可以等到等式c2=(a+b)2−4×

在图10 中,根据“割”法,可以等到等式c2=(b −a)2,分别整理这两个等式,你能得到什么结论?

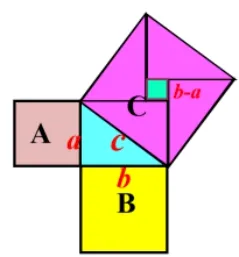
图10

教学分析: 在网格中,学生学会了割补法求正方形C的面积,那么去掉网格,也可以用同样的方法计算.正方形C的面积有两种表示方法,一种是边长的平方即c2;一种是用含a、b的式子表示,根据等面积法即可得到一个等式,化简整理之后有a2+b2=c2.猜想是逼近结论关键的一步,以命题的形式出现,使学生认识到一个命题只有经过证明是正确的才能成为定理.在探索的过程中,经历了正方形的边长由具体数到一般字母的表示过程,体现了从特殊到一般的数学思想方法.追问怎样证明两个直角三角形全等,让学生发现根据“角角边”可以证明全等.而这是“一线三等角”的全等模型,利用同样的方法可以证明任意两个直角三角形都是全等的.通过追问全等,又让本节课的学习上升了一个高度,实现了数学原理教学的深度学习.

环节5: 归纳勾股定理

通过割补法证明了猜想是正确的,因此我们把它叫做定理.在我国古代,古人把较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”,因此称此定理为勾股定理.

问题5: 勾股定理: 如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2.根据文字语言、图形语言,你可以写出它的符号语言吗?

追问: 你能说出勾股定理的几何意义吗?

教学分析: 向学生讲述勾股定理的由来,一方面增强了本节课的趣味性, 另一方面又让学生理解数学来源于生活.经历演绎推理的探究过程,让学生学会根据图形归纳出勾股定理的文字语言,又要求其说出勾股定理的符号语言.通过理解勾股定理的几何意义,让学生再次回顾探究勾股定理的起点是研究正方形的面积关系.

环节6: 勾股定理的数学文化史

问题6: 我国古代研究勾股定理的成就有哪些呢? 请看小视频.

图11

图12

教材分析: 通过对赵爽弦图的介绍,让学生了解我国古代数学家对勾股定理的发现以及证明作出的贡献,增强名族自豪感,激发学生的爱国热情.

环节7: 勾股定理的简单应用

练习: 图中所有的三角形都是直角三角形,四边形都是正方形,已知S1= 1,S2= 3,S3= 2,S4= 4,求S5,S6,S7的值.

图13

图14

教学分析: 结合勾股定理的发现过程,设置与之相关的习题,巩固定理的学习过程.通过把一个正方形的面积分成若干个小正方形的面积的和,如果不断地分下去,就可以得到一棵美丽的勾股树.

环节8: 课堂小结

问题7: (1)本节课我们学习了什么内容?

(2)本节课证明勾股定理的基本思路和方法是什么?

(3)我们经历了怎样的学习过程从而掌握了勾股定理?

设计意图: 通过小结突出本节课的重点,让学生对所学知识的结构有一个清晰的认识,形成良好的认知结构,学会一些解决问题的思想方法,体会数学的应用价值.让学生有机会体会和认识一些数学本源性问题,使学生理解数学知识的本质.

6 教学思考与感悟

6.1 构建逻辑连贯的数学知识结构,凸显整体思想

章建跃博士说过“日常教学,概念一个个地教,定理一个个地学,容易迷失在局部,见木不见林.长此以往就会导致坐井观天、思路狭窄、思维呆板,局限于一招一式的雕虫小技而不能自拔.把握好整体性,对内容的系统结构了如指掌,心中有一张‘联络图’,才能把准教学的大方向,才能教学有的放矢.也只有这样,才能使学生学到结构化、联系紧密的、迁移能力强的知识[2].”基于单元整体教学出发,笔者先是复习三角形的相关知识,建构等腰三角形、等边三角形的边、角特征.经过探究角的数量关系可以决定三角形的形的特征,由形的特征转化可得到边的数量关系,它把形和数密切联系了起来.当三角形的一个角等于90°时,得到一个直角三角形,直角三角形角的特征是两个锐角互余,提问直角三角形的三边之间有怎样的数量关系,利用启发性问题开启了探索直角三角形三边关系之旅.

6.2 创设具有深度思维的问题串

问题是教学的起点,也是教学的主线,除此之外,问题本身还具有激发学生求知欲和探究欲的功能.“好”问题能增强学生的学习热情和欲望,引发他们深层次的思考,引导他们探究学习,自主建构知识体系,从而促使学生在解决问题的过程中不断积累数学学习方法[3].由毕达哥拉斯的发现引入,从探究等腰直角三角形入手, 发现三个正方形的面积关系,根据正方形的面积计算公式得到三个正方形围成的等腰直角三角形的三边满足关系式: 两条直角边的平方和等于斜边的平方.接着提出问题: 一般的直角三角形三边之间是否也满足这种关系呢? 在网格中,以直角三角形的三边长为边向三角形的外部画出三个正方形,并计算出三个正方形的面积,由面积关系进一步推导直角三角形三边关系.于是猜想: 任意一个直角三角形,两直角边长分别为a、b,斜边长为c的直角三角形,三边之间满足a2+b2=c2.在网格背景下,通过观察和分析等腰直角三角形及一般的直角三角形三边关系,为形成猜想提供了典型特例,于是猜想的形成变得水到渠成.如果没有格点,那么如何证明呢? 巧妙过渡到猜想一般直角三角形的结论也成立,从而实现由特殊到一般的飞跃,有效引导学生经历定理的发现,猜想和验证的全过程.割补法证明以及如何想到割补法是学生思维的难点,教学中,教师通过问题铺垫,借助网格三角形以及网格的隐藏与再现,巧妙化解难点,有效促进学生思维的发展.

6.3 数学史有效融入课堂教学

数学大师吴文俊先生曾说,数学教育与数学史是分不开的.《义务教育数学课程标准(2011年版)》强调:“数学文化作为教材的组成部分,应渗透在整套教材中,使学生体会数学在人类发展历史中的作用,激发学生学习数学的兴趣[4].”笔者在录制的微课小视频中,先是介绍了我国古代赵爽证明勾股定理的方法,接着梳理了我国古代数学家研究勾股定理的许多杰出成果.利用绘制时间轴的形式介绍了我国从公元前21 世纪大禹治水→公元前1100年→公元前6、7 世纪→公元前3 世纪→公元250年→2002年在北京召开国际数学大会,大会的会徽就是赵爽弦图.通过介绍勾股定理的相关历史和文化,让学生对勾股定理产生浓厚的兴趣,激发学生热爱祖国的思想感情,培养民族自豪感.