改进均衡分布适配的滚动轴承寿命阶段识别

吴昊年　陈仁祥　胡小林　张霞　张焱　唐林林

摘要： 针对不同工况下训练样本与测试样本分布差异导致滚动轴承寿命阶段无法被有效识别的问题，提出改进均衡分布适配的滚动轴承寿命阶段识别方法。采用无重复均匀随机抽样对源域类间样本进行多次均匀随机抽样，得到源域多样本训练集，以减小源域内部样本选择对目标域预测标签的影响;在再生核希尔伯特空间上利用平衡因子μ动态调节边缘分布和条件分布所占权值，并通过迭代的方式不断优化目标域伪标签以减小两域的最大均值差异;利用源域多样本数据集各自的映射矩阵构造多个分类器，经过一致性判别得到目标域样本最终识别结果。在两组滚动轴承寿命阶段数据集上进行实验验证，证明了所提方法的可行性和有效性。

关键词： 故障诊断; 滚动轴承; 寿命阶段识别; 条件概率分布; 边缘分布

中图分类号： TH165⁺.3; TH133.33; TN911.7    文献标志码： A    文章编号： 1004-4523（2021）01-0194-08

DOI：10.16385/j.cnki.issn.1004-4523.2021.01.022

引 言

滚动轴承作为旋转机械关键零部件之一，对其寿命阶段识别可以监测其性能衰退过程，有效防止重大安全事故的发生。为准确识别滚动轴承寿命阶段，国内外已开展了相关研究。如：Yu等^[1]提出多域特征融合和降维学习的滚动轴承退化状态识别方法;陈仁祥等^[2]提出基于振动敏感时频特征的航天轴承寿命状态识别方法;王冰等^[3]提出了基于模糊聚类的退化状态识别方法。以上方法对同种工况下滚动轴承寿命阶段识别效果明显。但在不同工况下，可获得的训练样本数目有限，且训练数据与测试数据不满足独立同分布条件，降低了传统机器学习寿命识别模型的泛化能力，甚至使得模型不适用。

近年来，迁移学习以其跨领域、跨任务学习的优势在各领域得到了广泛应用^[4?5]。在机械研究领域，解决寿命阶段识别问题时，往往借鉴故障诊断方法。沈飞等^[6]将奇异值分解与迁移学习用于不同工况下的电机轴承故障的识别;段礼祥等^[7]将迁移成分分析应用于不同工况下的齿轮箱故障诊断;康守强等^[8]利用多核半监督迁移成分分析方法解决了变工况下滚动轴承故障诊断问题。上述方法关注于最小化域之间的边缘分布差异以达到较好的适配效果。然而在实际工程中，外在摩擦力、温度、工况条件等因素的变化，使得采集到的标记数据和目标域轴承寿命阶段数据分布特性差异较大，将两种概率分布的重要性同等对待，往往导致对滚动轴承寿命阶段识别效果不佳。Wang等^[9]针对实际应用中边缘分布适配和条件分布适配并不是同等重要的问题，提出了均衡分布适配方法（Balanced Distribution Adaptation， BDA），通过平衡因子适配两域分布取得了不错效果。然而BDA方法构建的单一弱分类器具有局限性，无法较好完成不同工况条件下寿命阶段样本的识别任务。

为解决上述问题，本文提出改进均衡分布适配的滚动轴承寿命阶段识别方法。首先，通过无重复均匀随机抽样，对源域类间样本进行多次等量隨机抽样得到源域多样本训练集，分别在目标域上预测其伪标签，避免了源域样本的选择对目标域预测标签的影响;随后，将源域多样本训练集与目标域测试样本集共同映射到再生核希尔伯特空间中，利用平衡因子μ动态调节边缘分布和条件分布所占权值，适配轴承不同寿命阶段数据两域分布差异;最后，通过多个分类器识别目标域寿命阶段数据，经一致性判别获得最终识别结果。在两组滚动轴承寿命阶段数据集上进行验证，证明了本文方法能有效识别不同寿命阶段样本，提高了识别准确率。

2.2 改进均衡分布适配的滚动轴承寿命阶段识别流程

根据上文论述，为实现改进均衡分布适配的滚动轴承寿命阶段识别，其实现流程图如图1所示。该算法实现主要包括：

1）样本特征提取。由于单域特征评估效果不足，本文提取多域特征构建高维特征集。包括16维时域特征和12维频域特征，8维db3小波3层小波包能量特征，8维db3小波3层小波包相对能量特征，8维db3小波3层小波包能量谱熵以及振动信号幅值谱熵、倒谱熵、自相关谱熵和奇异值谱熵等共56维特征。

2）源域多样本训练集与目标域训练集构建。对于源域标记数据，采用无重复均匀随机抽样从M种寿命阶段样本中抽取n个，得到一个源域单样本训练集，训练集大小为M×n。重复上述过程k次，得到源域多样本训练集。其中k个单样本训练集，每个待识别阶段均为M。对于目标域未标记数据，从中每次每类抽取等量样本构建测试集，待识别阶段为M种。

3）同一标记空间重构。将源域多样本训练集与目标域测试集共同映射至?空间中，k个源域单样本训练集各自为待识别目标域数据集赋予伪标签。通过平衡因子μ动态调节两域分布，执行两域类内、类间知识迁移不断优化伪标签。

4）输出识别结果。构造多个分类器分别识别重构后目标域寿命阶段特征，通过一致性判别方法输出最终识别结果。由于KNN分类器具有计算简单，易于实现，无需参数估计和训练的优点。本文选择KNN分类器用于伪标签的预测和最终结果的分类。

3 全寿命周期数据实验验证

3.1 实验设备及参数设置

实验采用PRONOSTIA实验台采集的IEEE PHM2012 Data Challenge^[11]加速寿命实验振动信号数据进行实验验证和分析。此数据采样频率为25.6 kHz，采样间隔为10 s，每个样本采样时间为0.1 s。PRONOSTIA实验平台如图2所示。

该数据集包含多个工况条件下的全寿命周期实验数据，选择3种工况条件下的滚动轴承全寿命周期振动信号数据，数据工况信息如表1所示。

滚动轴承从全新装配到完全失效的整个寿命周期共经历3种寿命阶段：磨合期、有效工作期和衰退期。实验设置3种工况条件下数据样本集：1）工况A为1650 r/min，4200 N数据样本集;2）工况B为1500 r/min，5000 N数据样本集;3）工况C为1800 r/min，4000 N数据样本集。为了更好地完成寿命阶段识别实验，利用文献[12]的方法划分不同工况的3种寿命阶段时，截取阶段明显的寿命阶段样本，把不明确样本进行了少量剔除。具体每个寿命阶段样本数分布如表2所示。

3.2 改进均衡分布适配方法实验分析

本实验主要验证不同工况下源域少标记且目标域完全没有标记时，改进均衡分布适配方法对异分布寿命阶段数据识别效果。训练样本采用无重复随机抽样从B工况3个寿命阶段中各抽取10，20和30个，获得3个寿命阶段共30，60，90个为一个源域样本集（为使实验符合实际工程中训练数据获取困难的情况，抽取的源域单样本数量占整个B工况源域样本数量的2.4%，4.8%，7.2%），抽取1000次得到1000个源域多样本数据集。

设置A工况与C工况样本为测试样本，数量分别为30，60，90。提取56维特征构建高维特征集，对此轴承数据进行不同工况下寿命阶段识别结果如表3所示。

从表3中可以看出，本方法在不同工况下滚动轴承寿命识别上表现良好。随着训练样本数量的增多，识别率也呈缓慢增加的趋势。不同转速与负载的工况下平均识别率在90%左右，样本数量在60左右已经能达到很好的效果。

为验证改进均衡适配算法较原方法识别精度明显提高。选择B工况训练60个样本，A工况测试60个样本，将整个寿命阶段样本作为源域单样本BDA，无重复均匀随机抽样得到改进均衡分布适配方法进行实验对比。为直观对比结果将源域多样本数据集得到的诊断结果直接求平均值，称为源域多样本平均。对比结果如图3所示。

由图3可知，由于目标域没有标签，只能通过源域数据直接预测其伪标签，所以源域内部样本的选择直接影响识别结果。而单分类器识别能力有限，样本数量对源域单样本识别影响不大。而本文方法反映了识别率与训练样本数目呈正相关的规律，凭借改进均衡分布适配方法动态调节两域分布重要性的优势，更好地最小化了域间分布差异，提升了识别率，平均达到92.29%;与源域多样本平均对比可得，随着不同源域样本在各自分类器上预测目标域伪标签，样本数量与准确率呈正相关规律;且多分类器集成后使最终识别精度大大提升。

3.3 改进均衡分布适配的迭代次数N与μ的选择

改进均衡分布适配方法涉及两个主要参数：1）迭代次数N;2）平衡因子μ。文献[9]对这两个参数的选择方法已经进行了讨论。N值的设置不宜过大，选择适当的值既可以节约运算时间又能保证识别的准确率。经过交叉验证实验，本文取N=20。平衡因子μ決定了边缘分布和条件分布哪个应该被优先考虑，其取值直接决定识别精度，图4详细展示了平衡因子适配效果（以B工况到A工况的迁移为例）。

根据图4（a）可知，B工况样本边缘概率分布与A工况相差较小，并不是影响适配的主因。故针对本组数据，条件分布的重要性要高于边缘分布，应设置μ>0.5，适配结果如图4（b）所示。结合图4（d）验证得知μ值在0.5?0.7之间时，识别率均达到90%以上，在0.6时取得最优值，识别准确率达到97.78%。最终分类结果通过t?SNE可视化为图4（c），其中M，S和D分别代表3种寿命阶段，test代表测试样本。所提识别方法明显区分了3种寿命阶段样本。

3.4 与传统机器学习降维方法对比

为了验证改进均衡分布适配方法降维后可以很好地保留数据样本本身属性，将本文方法与传统降维方法进行对比。结合文献[13?14]，本实验中SVM均采用高斯核函数，宽度为1;PCA与KPCA均采用径向基核函数，核参数γ=15，BDA采用迭代次数N=20，正则化参数λ=0.01，平衡因子μ=0.6。

由图5可以看出，训练样本与测试样本维数从1增加到11附近时，本文方法与KPCA，PCA结合SVM的3种方法的准确率不断提高。当维数超过11后，传统机器学习方法的识别率不高且伴随波动，而改进BDA方法的准确率总体保持平稳并略有提高，均明显高于KPCA和PCA两种方法。

造成这样的原因是PCA、KPCA作为传统机器学习的降维方法，它们在降维过程中不需要领域知识，忽略了领域间的差异。通过将两域中的所有样本映射到一个子空间来进行全局特征变换，没有考虑寿命阶段类别的内部关联性。这种全局特征变换方式，只能在一般超平面上学习两域异分布数据（超平面是松散的），导致其无法类内相关联，各寿命阶段样本内部不具关联性。

3.5 与其他迁移学习算法对比

为验证不同工况下，均衡分布适配在迁移上的优势，将改进均衡分布适配方法与迁移成分分析方法^[10]（Transfer Component Analysis，TCA）、联合分布适配方法^[15]（Joint Distribution Adaptation，JDA）、测地线流式核方法^[16]（Geodesic Flow Kernel，GFK）等迁移学习方法对比。源域仍采用工况B的训练集，目标域采用工况A和C的测试集，对比结果如表4所示。

由表4可见， TCA通过适配边缘分布，将全局域特征进行变换，不能很好处理不同寿命阶段间数据的区分性。JDA虽然考虑到两种分布对数据样本的影响，却没有根据具体数据衡量两种分布各自的重要性，泛化能力较差。GFK将原始特征变换到流形空间，最近距离的选择高度依赖于流形核的构建，对复杂分布适应性较弱。本文方法通过自适应的适配两域权值，有效地解决了不同工况下滚动轴承寿命阶段识别的问题，平均识别精度达到91.85%。特别是在BDA方法中，当μ=0时，BDA方法退化为TCA;当μ=0.5时，BDA退化为JDA。这两种算法都可以看作是BDA的特殊情况。

4 角接触球轴承实验验证

4.1 角接触球轴承寿命状态识别

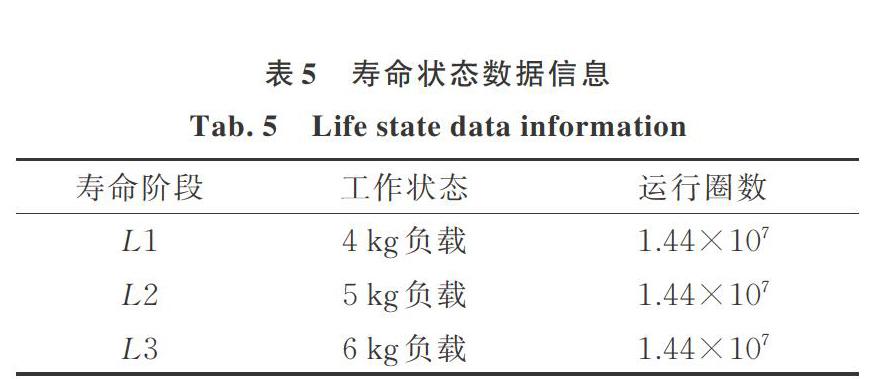
为验证本文构建的模型在不同型号轴承上的效果，现采用自测C36018型角接触球轴承，节径15 mm，包含7个滚动体，接触角度15°。在相同转速、不同负载下运行相同圈数，分别以L1，L2和L3表示 ，在运行圈数和转速相同的条件下，负载越大，寿命损耗越多，故3种不同负载对应3个不同寿命阶段，实际寿命损耗为L1<L2<L3。具体寿命状态信息如表5所示。

采用不同工况条件对处于不同寿命阶段的滚动轴承进行振动信号采集，采集时运行转速分别为500，1000和1500 r/min，加载负荷均为1 kg，采样频率均为25.6 kHz，采样长度均为102400，每种寿命阶段采样2次，对每种工况下各寿命阶段数据以2048为分析点数。1 kg载荷、500 r/min转速记为D工况，以1 kg载荷、1000 r/min转速的采集工况数据记为E工况，以1 kg载荷、1500 r/min记为F工况，各工况L1，L2和L3壽命阶段样本各100个。

设置D工况数据为源域数据，F、E工况数据为目标域数据。从源域每类样本中分别抽取1，2，3个即训练样本3，6，9个（所占比例为整个源域寿命阶段样本数的1%，2%，3%）。目标域每类样本中抽取10，20，30和40个，测试样本数分别为30，60，90和120个构成测试样本集。源域多样本数为100个。采用本文方法对角接触球轴承不同工况下滚动轴承寿命识别，设置μ=0.3，N=20，识别结果如表6所示。

从表6可以看出，本文方法在角接触球轴承不同工况下寿命阶段识别上表现良好。很好地适应了目标域数据完全无标记的适配问题，针对不同工况下分布差异较大的数据，平均识别精度最高可达95.67%。

4.2 与其他迁移学习算法对比

改进均衡分布适配方法与TCA，JDA和GFK等迁移学习方法对比。选择源域3样本为训练集（所占比例为整个源域寿命阶段样本数的1%），目标域60（所占比例为整个目标域寿命阶段样本数60%）样本为测试集对比识别结果，得到如表7所示。

本节实验利用不同工况下角接触球轴承的数据证明了改进均衡分布适配方法的可行性。无论是在与传统机器学习还是迁移学习方法的对比中都具有明显的优势。实验结果表明改进均衡分布适配方法很好的完成了滚动轴承寿命阶段识别的任务，识别准确率达到94%左右。

5 结 论

1）改进均衡分布适配方法，采用无重复均匀随机抽样对源域类间样本进行多次均匀随机抽样得到多个训练样本，充分发掘了类间样本的潜在信息，减少了迭代造成的误差，更好地为无标记的目标域空间提供了可适配的伪标签;

2）在再生核希尔伯特空间，调节平衡因子μ以适配两域边缘分布与条件分布所占权值，伴随定量随机抽样提高了数据类内紧凑性和类间区分性，大大提升了滚动轴承寿命阶段识别的精确率;

3）改进均衡分布适配方法与其他领域适应性方法对比识别结果。说明源域与目标域的边缘概率与条件概率在适配过程中各自的重要性不能被同等看待。改进均衡分布适配方法对不同工况下滚动轴承寿命阶段的识别效果更佳。

参考文献：

[1]        Yu H， Li H R， Tian Z K， et al. Rolling bearing degradation state identification based on LPP optimized by GA[J]. International Journal of Rotating Machinery， 2016， 2016：9281098.

[2]        陈仁祥， 黄 鑫， 杨黎霞，等. 加噪样本扩展深度稀疏自编码神经网络的滚动轴承寿命阶段识别[J]. 振动工程学报， 2017， 30（5）：874-882.

CHEN Renxiang， Huang Xin， Yang Lixia， et al. Bearing life state recognition using deep sparse auto-encoder neural network with noise adding sample expansion[J].Journal of Vibration Engineering， 2017， 30 （5）： 874-882.

[3]        王 冰， 王 微， 胡 雄，等. 基于GG模糊聚类的退化状态识别方法[J]. 仪器仪表学报， 2018，39（3）： 21-28.

WANG Bing， Wang Wei， Hu Xiong， et al. Degradation condition recognition method based on Gath-Geva fuzzy clustening[J]. Chinese Journal of Scientific Instrument， 2018，39（3）： 21-28.

[4]        Pan S J， Yang Q. A Survey on transfer learning[J]. IEEE Transactions on Knowledge & Data Engineering， 2010， 22（10）：1345-1359.

[5]        庄福振，罗 平，何 清，等.迁移学习研究进展[J].软件学报，2015， 26（1）：26-39.

Zhuang Fuzhen， Luo Ping， He Qing， et al. Research progress of migration learning[J]. Journal of Software， 2015， 26 （1）： 26-39.

[6]        沈 飞， 陈 超， 严如强. 奇异值分解与迁移学习在电机故障诊断中的应用[J]. 振动工程学报， 2017， 30（1）：118-126.

SHEN Fei， CHEN Chao， YAN Ruqiang. Application of singular value decomposition and transfer learning in motor fault diagnosis[J].Journal of Vibration Engineering， 2017， 30 （1）： 118-126.

[7]        段禮祥， 谢骏遥，王 凯，等. 基于不同工况下辅助数据集的齿轮箱故障诊断[J]. 振动与冲击， 2017， 36（10）：104-108.

DUAN Lixiang， XIE Junyao， WANG Kai， et al. Gearbox fault diagnosis based on auxiliary data sets under different working conditions[J]. Journal of Vibration and Shock， 2017， 36 （10）： 104-108.

[8]        康守强， 胡明武， 王玉静，等. 基于特征迁移学习的变工况下滚动轴承故障诊断方法[J]. 中国电机工程学报， 2019，39（3）： 764-772.

KANG Shouqiang， HU Mingwu， WANG Yujing， et al. Fault diagnosis method of rolling bearing under variable conditions based on feature transfer learning [J]. Proceedings of the CSEE， 2019，39（3）：764-772.

[9]        Wang J， Chen Y， Hao S， et al. Balanced distribution adaptation for transfer learning[C].IEEE International Conference on Data Mining， 2017.

[10]      Pan S J， Tsang I W， Kwok J T， et al. Domain adaptation via transfer component analysis.[J]. IEEE Transactions on Neural Networks， 2011， 22（2）：199-210.

[11]      Li X， Lu W F， Zhai L， et al. Predictive modeling for life cycle reliability analysis and machine health condition prediction in remanufacturing[M]. London： Springer， 2014.

[12]      阙子俊， 金晓航， 孙 毅. 基于UKF的轴承剩余寿命预测方法研究[J]. 仪器仪表学报， 2016， 37（9）：2036-2043.

Que Zijun， JIN Xiaohang， SUN Yi. Remaining useful life prediction for bearings with the unscented Kalman filter-based approach[J]. Chinese Journal of Scientific Instrument， 2016， 37 （9）： 2036-2043.

[13]      Guo S， Deng F， Jie C， et al. Sensor multi-fault diagnosis with improved support vector machines[J]. IEEE Transactions on Automation Science & Engineering， 2017， 14（2）：1053-1063.

[14]      Deng X， Tian X， Chen S， et al. Deep learning based nonlinear principal component analysis for industrial process fault detection[C]. International Joint Conference on Neural Networks （IJCNN 2017）. IEEE， 2017.

[15]      Long M， Wang J， Ding G， et al. Transfer feature learning with joint distribution adaptation[C]. IEEE International Conference on Computer Vision， Sydney， NSW， 2013： 2200-2207.

[16]      Gong B， Shi Y， Sha F， et al. Geodesic flow kernel for unsupervised domain adaptation[C].IEEE Conference on Computer Vision & Pattern Recognition， 2015.

Abstract： In view of the problem that the distribution differences between training samples and test samples under different working conditions cannot effectively identify the life stage of rolling bearings， an improved method for identifying the life stage of rolling bearings based on balanced distribution is proposed. Firstly， non-repetitive uniform random sampling is used to conduct multiple uniform random sampling of inter-class samples in source domain， the training set of multi-sample in source domain is obtained to reduce the influence of sample selection in source domain on target domain prediction label. Furthermore， the weights of edge distribution and conditional distribution are dynamically adjusted in reproducing kernel Hilbert space by using equilibrium factorμ，  the weights of edge distribution and conditional distribution are continuously optimized by iteration. In order to reduce the maximum mean difference between the two domains， pseudo-labels in the target domain are transformed into pseudo-labels. Finally， multiple classifiers are constructed by using the mapping matrices of the source domain data sets， the final recognition results of the target domain samples are obtained by consistency discrimination. Experiments on two sets of data sets of rolling bearing life stages show that the proposed method is feasible and effective.

Key words： fault diagnosis; rolling bearing; life state identification; conditional probability distribution; marginal distribution

作者簡介： 吴昊年（1993-），男，硕士。电话：（023）62539903;E-mail：296018167@qq.com

通讯作者： 陈仁祥（1983-），男，博士，教授，博士生导师。电话：（023）62539903;E-mail：manlou.yue@126.com