非经典阻尼分布参数系统复振型叠加方法
2021-06-06陈华霆谭平
陈华霆 谭平


摘要: 附加减震装置的一维桿或剪切梁模型属于非连续的非经典阻尼分布参数系统。对于它的动力分析,通常是建立分段的运动方程,然后利用各段动力反应的实振型叠加形式和连续条件进行动力计算。这是一种实模态综合方法,尽管它可以求得近似的动力反应,但反映不出阻尼对整体系统动力特性的影响。为了考虑附加减震装置引起的阻尼和刚度非连续性,基于广义函数理论,建立了整体系统的无量纲化运动方程,利用Laplace变换推导了振型函数和特征值方程,并给出了振型函数的正交条件,最终导出了适用于非经典阻尼分布参数系统的复振型叠加方法。由于特征值方程为复杂的超越方程,为了同时求出多个自振频率,建议了一种基于柯西积分定理的等效多项式方法。这种方法将自振频率转变成了线性代数方程组的求解,更简便、实用。最后以基底隔震分布参数系统为例,展示了复振型叠加法的应用,同时对隔震结构设计得出了有益的结论。给出的复振型叠加法是传统的经典阻尼连续系统实振型叠加法的推广,具有一定理论意义和应用价值。
关键词: 线性振动; 非经典阻尼; 分布参数系统; 动力分析; 复振型叠加方法
中图分类号: O321; TU311.3 文献标志码: A 文章编号: 1004-4523(2021)01-0048-12
DOI:10.16385/j.cnki.issn.1004-4523.2021.01.006
引 言
对于线性振动系统,通常采用振型叠加法进行动力分析。由于系统振动一般是低阶振型起主导作用,因此,振型叠加法可以仅取前若干阶振型参与计算,从而很大程度地降低计算量。按照阻尼分布的特点,可将线性系统分为经典阻尼系统和非经典阻尼系统。前者可采用传统的振型叠加法进行动力分析,这种方法基于无阻尼振型,通常也称为实振型叠加法。若系统中附加了额外阻尼,则阻尼矩阵就不满足无阻尼振型解耦的Caughey条件[1?2],而成为非经典阻尼矩阵。这时,就需要采用复振型叠加法。这种方法首先由Traill?Nash[3]和Foss[4]提出,而后经过许多学者[5?8]的研究得以不断完善。目前,在减震控制结构中已有较好的应用[9?12]。
当前,复振型叠加法的研究主要集中在有限自由度离散系统,而实际结构都是具有连续分布特性的无限自由度体系,将结构离散为有限自由度进行求解只能获得结构真实动力行为的近似解。同时,对某些特殊结构,如桥梁、烟囱、拱坝等,采用分布参数模型(偏微分方程)来描述其动力行为更为合理[13?14]。此外,基于分布参数模型更容易发现、解释一些物理现象,如波的传播。在分布参数模型中,一维杆或剪切梁模型是最简单的模型,但在实践中是一个很好的力学模型。例如,可以用来研究多层框架结构的动力特性[15]。另外,这类模型还可以安装阻尼装置用来研究振动控制问题,如Skinner等[16]用剪切梁模型研究了隔震结构的动力特点,深海开采系统中钻杆的振动控制、地震作用下桥梁的纵向减震问题也可以采用一维杆或剪切梁模型来描述其动力行为[17?18]。由于一维杆和剪切梁模型具有相同的运动方程,本文统一用一维杆来表述。
关于无阻尼一维杆的振动问题可详见文献[13?14,19?21]。附加阻尼装置的一维杆属于非经典阻尼系统。对于该系统的动力分析,目前仅限于几种特殊情况。如Singh等[22]给出了解析的含黏滞阻尼边界(黏滞阻尼器布置在杆端)的一维杆特征值方程和振型函数;Hull[23]研究了这种模型在集中荷载作用下的振型叠加法;Cortés等[24?25]将上述黏滞阻尼边界考虑为黏弹性边界推导了特征值方程和频响函数的解析表达式;Yüksel等[26?27]进一步研究了黏滞阻尼边界位于杆内部(黏滞阻尼器一端固定,另一端与杆内部一点相连)的情况。此外,对于这类非经典阻尼分布参数系统的动力分析,尚不能像离散系统那样基于复振型正交条件建立复振型叠加法,其关键问题在于附加阻尼装置的杆,沿轴线方向阻尼和刚度属性发生突变,属于非连续系统。这种非连续系统动力分析的经典方法是将整个杆在非连续点位置划分为若干段,对每一段分别建立运动方程,然后利用在非连续点位置位移或内力的连续条件和边界条件进行求解。文献[22?27]就是利用这种方法推导出的特征值方程和振型函数,但基于这种分段的振型函数建立正交关系就不是那么容易了。为了考虑阻尼装置引起的刚度和阻尼非连续性,本文采用广义函数理论对整个系统建立一个运动方程[28?32],从而求出的振型函数只有一个表达式。
为了方便公式推导,本文只考虑布置一个阻尼装置,这也很容易推广到多个阻尼装置的情况。本文首先基于广义函数理论,建立无量纲化的非连续杆系统的运动方程;然后,利用Laplace变换,推导在齐次边界条件下特征值方程和振型函数的解析表达式,并建立振型函数正交关系,推导杆在单位脉冲荷载、一般荷载、简谐荷载和支座激励作用的复振型叠加法表达式;同时,对于特征值方程的求解,本文采用一种基于柯西积分定理的等效多项式方法;最后,利用数值算例验证本文建议方法的有效性。
1 运动方程
非連续杆模型如图1所示,由AB和BC两段组成,总长为l,单位长度的质量、横截面面积、弹性模量分别为m,A,E。在x0位置,两段之间由弹簧和阻尼元件连接,其刚度系数、阻尼系数分别为k,c。整个杆在B点力学属性发生突变,属于非连续系统。传统的分析方法是分别对AB和BC段建立运动方程,即
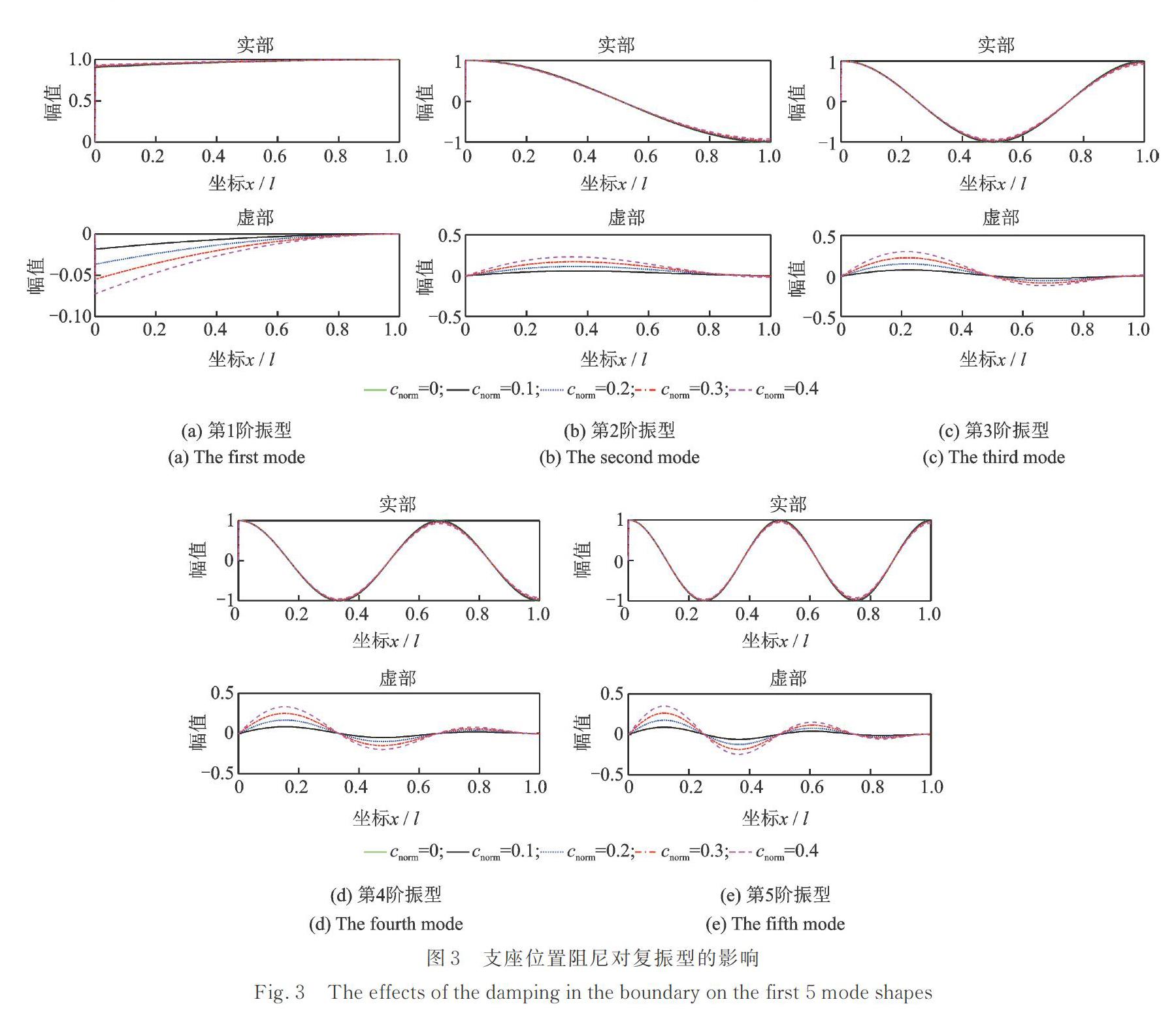
支座阻尼对复振型的影响如图3所示,其中实部曲线中绿色实线表示无阻尼实振型,其他4条曲线分别对应于cnorm=0.1,0.2,0.3,0.4,阻尼越大相应的虚部的幅值也越大。可以看出:复振型函数在支座位置处均有突变;阻尼对复振型实部基本没有影响,主要影响复振型的虚部,而虚部主要与空间质点的振动相位有关;同时,若不考虑阻尼,其振动形状与复振型实部的形态更为接近。
自由端位移、支座反力的频响函数幅值如图4?5所示,很明显在结构第1阶自振频率附近,随着阻尼的增大结构的响应是降低的,但随着输入频率的增大,阻尼的耗能效果降低,并出现增大结构响应的现象。这说明阻尼的耗能效果是受输入频率的影响,只有在较低的频率范围内才具有降低结构响应的作用;高频输入下,增加阻尼对结构不利。
图6?7给出了在3种输入频率下(ω=1.94,13.98和27.46 rad/s,分别对应于不考虑阻尼影响的隔震结构前3阶自振频率)离散质点系模型的响应,其中单元数目n取20,40,80和100四种情况。图中纵坐标表示离散质点系模型响应与本文建议的分布参数模型之比,横坐标表示隔震支座阻尼大小。在离散质点系模型频率响应计算中,忽略了阻尼的非经典特性,即采用强迫解耦方法,这也是实际中常用的方法。可以看出,在支座阻尼较小时,单元数目对响应影响较大,特别是高频输入下。此外,随着支座阻尼的增大,强迫解耦方法的误差越来越大,并且明显受输入频率的影响。如当ω=1.94 rad/s时,与精确值相比,强迫解耦方法计算出的支座反力随着支座阻尼的增大不断降低,而当ω=13.98 rad/s时,强迫解耦方法计算出的支座反力不断增大而后趋于稳定。显然,强迫解耦方法的适用性非常受限。在输入频率ω=1.94 rad/s时,若支座阻尼在0.15以内,支座反力精度可达到95%;而高频输入下,同样精度的适用阻尼变得非常小。
7 结 论
对于含阻尼装置的非连续杆模型,本文基于广义函数建立了无量纲化的运动方程,利用分离变量研究了这种非连续杆系统的复振型叠加方法。文中推导出了在齐次边界条件下的特征值方程,其为超越方程,为了求出一定数量的解,介绍了一种等效多项式方法,该方法比常用的基于Newton迭代的方法简单、有效。非连续的振型函数满足正交条件,可以用来解耦运动方程,给出了结构在单位脉冲荷载、一般荷载、简谐荷载和支座激励下的动力响应表达式,并且其与标准的单自由度运动方程相联系,便于实际应用。最后,利用一基底隔震系统对本文建议的复振型叠加法进行了有效性验证,其结果对隔震结构的设计具有一定的指导意义。
参考文献:
[1] Caughey A K. Classical normal modes in damped linear dynamic systems[J]. Journal of Applied Mechanics, ASME, 1960, 27(2): 269-271.
[2] Caughey A K, OKelly M E J. Classical normal modes in damped linear dynamic systems[J]. Journal of Applied Mechanics ASME, 1965, 32(3): 583-588.
[3] Traill-Nash R W. An analysis of the response of a damped dynamical system subjected to impress forces[R]. Australian Department of Supply, Aeronautical Research Laboratory Report, 1950, SM.151.
[4] Foss K A. Co-ordinates which uncouple the linear dynamic systems[J]. Journal of Applied Mechanics, Transactions of the ASME, 1958, 24:361-364.
[5] Traill-Nash R W. Modal methods in the dynamics of systems with non-classical damping [J]. Earthquake Engineering and Structural Dynamics, 1981, 9:153-169.
[6] Veletsos A S, Ventura C E. Modal analysis of non-classically damped linear systems[J]. Earthquake Engineering and Structural Dynamics, 1986, 14(2):217-243.
[7] Igusa T, Kiureghian A D, Sackman J L. Modal decomposition method for stationary response of non-classically damped systems[J]. Earthquake Engineering and Structural Dynamics, 1984,12(1):121-136.
[8] 陳华霆,谭 平,彭凌云,等.复振型叠加法截断误差及改进[J].振动工程学报, 2017, 30(4):556-563.
Chen H, Tan P, Peng L, et al. Truncation error and improvement of complex modal superposition approach[J]. Journal of Vibration Engineering, 2017,30(4):556-563.
[9] 周锡元,董 娣,苏幼坡.非正交阻尼线性振动系统的复振型地震响应叠加分析方法[J].土木工程学报,2003,36(5):30-36.
Zhou X, Dong D, Su Y. New method for linear systems with non-classical damping under ground motion [J]. China Civil Engineering Journal, 2003, 36(5): 30-36.
[10] Zhou X, Yu R, Dong D. Complex mode superposition algorithm for seismic responses of non-classically damped linear MDOF system[J]. Journal of Earthquake Engineering, 2004, 8(4):597-641.
[11] 周锡元,马东辉,俞瑞芳.工程结构中的阻尼与复振型地震响应的完全平方组合[J].土木工程学报,2005,38(1):31-39.
Zhou X, Ma D, Yu R. Damping in structures and complete quadratic combination (CCQC) of complex mode seismic responses[J]. China Civil Engineering Journal, 2005, 38(1): 31-39.
[12] 周锡元,俞瑞芳.非比例阻尼线性体系基于规范反应谱的CCQC法[J].工程力学,2006,23 (2):10-17.
Zhou X, Yu R. CCQC method for seismic response of non-classically damped linear system based on code response spectra?[J]. Engineering Mechanics, 2006, 23 (2):10-17.
[13] Clough R W, Penzien J. Dynamic of Structures[M]. 3rd ed. Berkeley, Califomia, USA: Computers and Structures Inc., 1995: 365-424.
[14] Chopra A K. Dynamics of Structures: Theory and Applications to Earthquake Engineering?[M]. 4th ed. USA: Prentice Hall, 2012: 698-724.
[15] 沈聚敏,周锡元,高小旺,等.抗震工程学[M].第2版.北京:中国建筑工业出版社, 2015:106-116.
Shen J, Zhou X, Gao X, et al. Aseismic Engineering[M]. 2nd ed. Beijing: China Architecture and Building Press, 2015: 106-116.
[16] Skinner R I, Robison W H, McVerry G H. An Introduction to Seismic Isolation[M]. Baffins Lane, Chichester, England: John Wiley & Sons Ltd., 1993:119-159.
[17] Aso K, Kan K, Doki H, et al. Effects of vibration absorbers on the longitudinal vibration of a pipe string in the deep sea―Part 1: In case of mining cobalt crust[J]. International Journal of Offshore and Polar Engineering, 1992,2(4):309-317.
[18] Feng Q, Shinozuka M. Control of seismic response of bridge structures using variable dampers[J]. Journal of Intelligent Material Systems and Structures, 1993,4: 117-122.
[19] 廖振鹏.工程波动理论导论[M].第2版.北京:科学出版社, 2002:67-81.
Liao Z P. Introduction to Wave Motion Theories in Engineering[M]. 2nd ed. Beijing: Science Press, 2002:67-81.
[20] Graff K F. Wave Motion in Elastic Solids[M]. New York: Dover Publications Inc., 1991:75-133.
[21] Kinsler L E, Frey A R, Coppens A B, et al. Fundamentals of Acoustics?[M]. 4th ed. New York: John Wiley & Sons Inc., 2000:68-86.
[22] Singh R, Lyons W M, Prater G. Complex eigensolution for longitudinally vibration bars with a viscously damped boundary[J]. Journal of Sound and Vibration, 1989, 133(2): 364-367.
[23] Hull A J. A closed form solution of a longitudinal bar with a viscous boundary condition[J]. Journal of Sound and Vibration, 1994, 169(1): 19-28.
[24] Cortés F, Elejabarrieta M J. Longitudinal vibration of a damped rod. Part I: Complex natural frequencies and mode shapes?[J]. International Journal of Mechanical Science, 2006,48(9): 969-975.
[25] Cortés F, Elejabarrieta M J. Forced response of a viscoelastically damped rod using the superposition of modal contribution functions?[J]. Journal of Sound and Vibration, 2008,315(1-2): 58-64.
[26] Yüksel S, Gürg?ze M. Continuous and discrete models for longitudinally vibrating elastic rods viscously damped in-span[J]. Journal of Sound and Vibration, 2002, 257(5): 996-1006.
[27] Yüksel S, Dalli U. Longitudinally vibrating elastic rods with locally and non-locally reacting viscous dampers [J]. Shock and Vibration, 2005, 12(2): 109-118.
[28] Yavari A, Sarkani S, Moyer E M Jr. On the applications of generalized functions to beam bending problems[J]. International Journal of Solids and Structures, 2000,37(40): 5675-5705.
[29] Zemanian A H. Distribution Theory and Transform Analysis[M]. New York: McGraw-Hill, 1965.
[30] Kanwal R P. Generalized Functions Theory and Applications[M]. New York: Academic Press, 1983.
[31] Schwarz L. Théorie des Distributions[M]. Paris: Hermann, 1966.
[32] Wang J, Qiao P. Vibration of beams with arbitrary discontinuities and boundary conditions?[J]. Journal of Sound and Vibration, 2007, 308(1-2):12-27.
[33] Jackson D. Non-essential singularities of functions of several complex variables[J]. The Annals of Mathematics, 1916, 17(4): 172-179.
[34] Jackson D. Roots and singular points of semi-analytic functions?[J]. The Annals of Mathematics, 1917, 19(2): 142-151.
[35] Luck R, Stevens J W. Explicit solutions for transcendental equations?[J]. SIAM Review, 2002, 44(2): 227-233.
[36] Boyd J P. Solving Transcendental Equations: The Chebyshev Polynomial Proxy and Other Numerical Rootfinders, Perturbation Series, and Oracles[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2014.
[37] Luck R, Zdaniuk G J, Cho H. An efficient method to find solutions for transcendental equations with several roots[J]. International Journal of Engineering Mathematics, 2015: 523043.
Abstract: One-dimensional bar or shear-type beam with additional energy dissipation devices is a distributed-parameter system with non-classical damping. For its dynamic analysis, the conventional way is to construct an equation of motion for each segment and obtain the dynamic response by using the real mode superposition method and the continuous condition. In essence, this method is a component mode synthesis based on undamped modes of substructure. Even though approximated dynamic responses can be estimated, it cannot consider the effect of damping on the dynamic behavior. To consider the discontinuity of damping and stiffness resulting from the additional damper, utilizing the generalized function theory, one non-dimensional equation of motion for the whole system is constructed in this paper. Then, using the Laplace integral transformation, the eigen function (complex mode) and eigenvalue equation are derived. Finally, the complex mode superposition method for distributed-parameter systems with non-classical damping is developed based on the derived orthogonality condition of eigen functions. In addition, the eigenvalue equation is a very complex transcendental equation, in order to get several natural frequencies, an equivalent polynomial method based on the Cauchy integral theorem is proposed, in which the eigenvalue equation is transformed into a set of linear equations such that their solutions can be obtained more easily. In the last section of this paper, the application of the proposed method is illustrated in a base-isolated shear-type beam and some useful information for the design of base-isolated structures is provided. To summarize, the complex mode superposition method is an extension of the conventional real mode superposition method for classically damped continuous and distributed-parameter systems, which is meaningful and valuable in the theory and application.
Key words: linear vibration; non-classical damping; distributed-parameter systems; dynamic analysis; complex mode superposition method
作者简介: 陈华霆(1988-),男,讲师。电话:(020)86395053;E-mail: huntingchen@foxmail.com
通讯作者: 谭 平(1973-),男,研究员,博士生导师。电话:(020)86395007;E-mail: ptan@foxmail.com
