高速列车盘形制动系统热机耦合特性分析

王东伟 ，吴 霄 ，项载毓 ，莫继良

（1. 中国核动力研究设计院核反应堆系统设计技术重点实验室，四川 成都 610213；2. 西南交通大学摩擦学研究所，四川 成都 610031）

随着我国高速列车运行速度的不断增大，列车在不同运行工况下的制动性能优劣程度已经成为了影响高速列车发展的首要问题[1]. 在列车制动过程中，制动盘和制动片在快速高压下发生剧烈的摩擦作用，释放出大量热能，对摩擦表面造成周期性热冲击并形成热斑，且由于热机耦合的作用，制动热对系统振动噪声和疲劳损伤均有重要的影响[2]. 因此，研究高速列车制动系统在热机耦合状态下的摩擦副表面温度场和应力分布特征，对探索新型制动盘表面的耐磨与抗疲劳途径，改善制动尖叫噪声，改进制动盘的使用寿命有重要的意义[3].

考虑到1∶1高速列车制动试验的复杂性和长周期等特点，大量研究者采用数值模拟的手段对制动过程进行模拟，以揭示制动系统的热机耦合动态特性[4-9]：刘静娟等[4]探讨了不同结构的筋板对制动盘散热性能的影响，得到了有利于改善制动盘散热性能的筋板分布结构；石晓玲等[5]建立了带裂纹的制动盘网格，并探讨了热机耦合作用下单条裂纹和多条裂纹的扩展规律；杨智勇等[6]充分考虑材料热传导的瞬态过程和材料高温下塑性变形的特性，进而进行弹塑性热机耦合求解，验证盘面局部热斑产生原因；周素霞等[7]建立制动盘无内热源的三维温度场分布的数学计算模型，对不同制动状态下的盘面温度和制动应力进行对比分析，为高速列车复合材料制动盘的热疲劳性能评价提供依据.

以上研究对认识高速列车制动系统热机耦合行为有重要意义，但是所建立的有限元模型往往过于简化（通常由盘和片组成），没有具体体现出制动系统的结构及制动力具体加载行为. 此外，热机耦合分析通常关注制动盘温度场和应力场的分布行为，对摩擦片的温度和应力分布以及热机耦合对制动器的接触行为和振动噪声特性所产生的影响并没有展开系统的研究. 因此有必要对不同结构的制动器热机耦合特性进行研究，探讨制动器结构和温度、振动三者之间的动态关系，从而为高铁制动器的选材和结构设计提供理论依据.

为此，本研究建立起高速列车盘式制动器有限元模型，采用热机直接耦合法研究制动过程中界面温度特征和动力学特性，重点探讨制动摩擦片表面径向和轴向的温度分布及弹性变形行为，并对有/无热机耦合状态下的系统动力学行为进行对比分析.研究结果为改善制动界面温度分布和制动闸片减振降噪的结构设计提供重要理论依据.

1 制动系统热机耦合分析理论

1.1 制动系统有限元模型

图1（a）为高速列车盘形制动系统三维有限元模型，模型主要包括制动盘、盘毂、背板、闸片、闸片托、制动夹钳和螺栓. 有限元模型的约束情况如图1（b）所示，考虑到制动盘与盘毂通过螺栓实现连接，在模型中二者设置为Tie约束. 约束制动盘内圈所有方向的平动自由度，保留制动盘在Y轴转动方向自由度；设置制动夹钳和闸片托之间形成Hinge连接，使夹钳在加载过程中实现力的传递；在夹钳后孔处定义耦合参考点，并对其分别施加沿Y轴方向的制动载荷，本研究中制动力F= 12 kN；闸片托与闸片背板之间、闸片背板和闸片之间均采用Tie约束，闸片与制动盘之间采用面—面接触.

图1 列车制动系统有限元模型和边界条件Fig. 1 Finite element model of the high speed train disc brake system and its boundary conditions

制动过程中随着摩擦界面温度的升高，制动盘和闸片的材料特性均随温度变化表现为非线性特性. 本研究采用的制动摩擦副材料参数与文献[10]一致. 采用四面体与六面体网格实现对制动系统模型的网格划分，具体部件网格特性见表1.

表1 有限元模型网格特征Tab. 1 Mesh characteristics of the finite element model

1.2 制动热分析方程及边界条件

高速列车在制动过程中，大部分的动能通过制动盘和闸片的摩擦作用转换成为热能，并在摩擦界面不断聚集，导致界面温度升高. 同时，由于暴露在空气之中，摩擦产生的热量不断以热传导、热辐射和热对流的方式与外界进行热交换，因此在模型计算过程中，需要对摩擦副热交换的过程进行定义[11].

1.2.1制动盘和闸片间的热传导分析

由于制动盘和闸片之间存在温度差，必然导致二者之间发生热量转移，可以把热传导的过程当作平壁导热过程进行求解，满足傅里叶定律，如式（1）.

式中：qT为热传导换热量；T1为摩擦面表面温度差；k为材料的热传导系数；A为导热面积.

1.2.2摩擦副与空气热对流分析

假设环境温度为20 ℃，则摩擦副由于温升将会对环境进行热量对流，符合牛顿冷却公式，如式（2）.

式中：qC为热对流换热量；Ta、Tg分别为空气和固体表面温度；λ为对流换热系数.

1.2.3 摩擦副辐射散热分析

热辐射是摩擦副向外发射能量的过程，可采用史蒂芬-玻尔兹曼方程来计算，如式（3）.

式中：qR为辐射散热量；ε为摩擦副材料的辐射率；σ为史蒂芬-玻尔兹曼常数；AF为辐射面面积;T4为辐 射面温度；T0为空气绝对温度.

2 制动系统热机耦合特性分析

2.1 闸片界面总体温度变化分析

首先对摩擦片的进出摩擦区域进行定义，如图2所示.

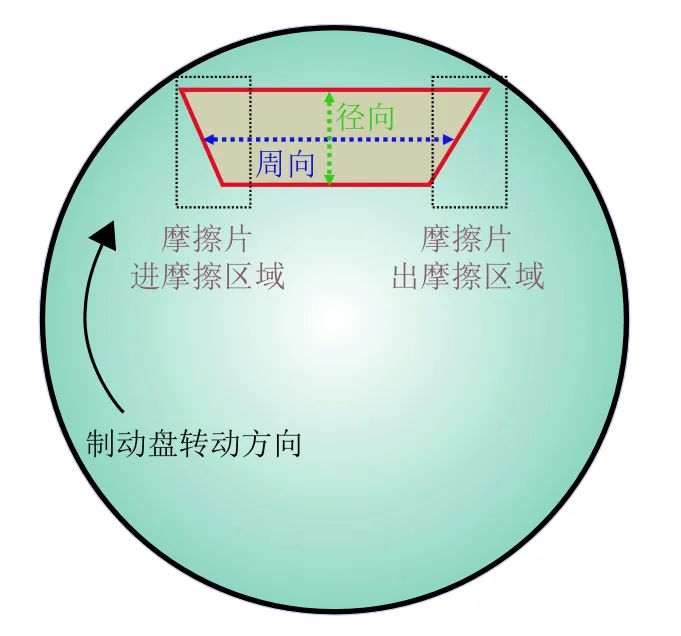
图2 摩擦片进出摩擦区域示意Fig. 2 Schematic of the in and out friction zone of pad

对制动器模型在热机耦合作用下制动盘闸片两侧的表面温度分布进行分析，结果如图3（a）所示.闸片温度在制动过程呈现出明显的不对称性，在制动摩擦的前期阶段，闸片进摩擦区域（摩擦片上首先进入与制动盘摩擦接触的区域）成为主要的高温区.这是由于制动过程中摩擦力引起的旋转压紧效应使得闸片进摩擦区域成为主要应力集中区域，因此温度迅速升高[12]. 随着制动过程的进行，制动盘和闸片均发生了不同程度的热翘曲变形，如图3（b）所示，尤其是当制动盘热变形开始挤压闸片中部时，摩擦片表面的最大应力集中区域逐渐发生了转移，闸片中部和出摩擦区域（摩擦片上首先离开与制动盘摩擦接触的区域）的温度逐渐升高. 当制动过程进一步进行时，此时闸片开始呈现出局部高温闪温现象，这是由于当制动进行到稳定阶段时，制动系统保持一定的振动模态接触方式进行运动，形成局部高温. 这也可以解释闸片中局部热斑的形成原因，因此摩擦衬片表面温度处于动态变化过程.

2.2 闸片表面周向温度和径向温度变化分析

2.2.1 闸片表面周向温度分布

为了进一步说明热机耦合作用下闸片表面温度分布特性，本部分对制动闸片表面3个区域（外径区、中间区、内径区）的周向温度分布进行分析，分别选取闸片3个区域的等间距周向排布节点（Nw1～Nw9，Nz1～Nz9，Nn1～Nn9），计算制动过程中节点周向温度分布情况，结果如图4. 由图4可知：可见在闸片的3个区域均出现了明显的热量集中的现象，在闸片外径区域，其进摩擦区域和出摩擦区域均形成了明显的高温区，节点Nw1、Nw3、Nw7和Nw9的温度均明显大于其他节点（图4（a））. 相比之下，在闸片中部区域，闸片靠近出摩擦区域成为高温集中区，节点Nz3温度在制动过程中明显高于其他节点温度（图4（b））；相反的是，在闸片内径区域，闸片靠近进摩擦区域成为高温集中区，节点Nn7温度在制动过程中出现显著增大（图4（c））.

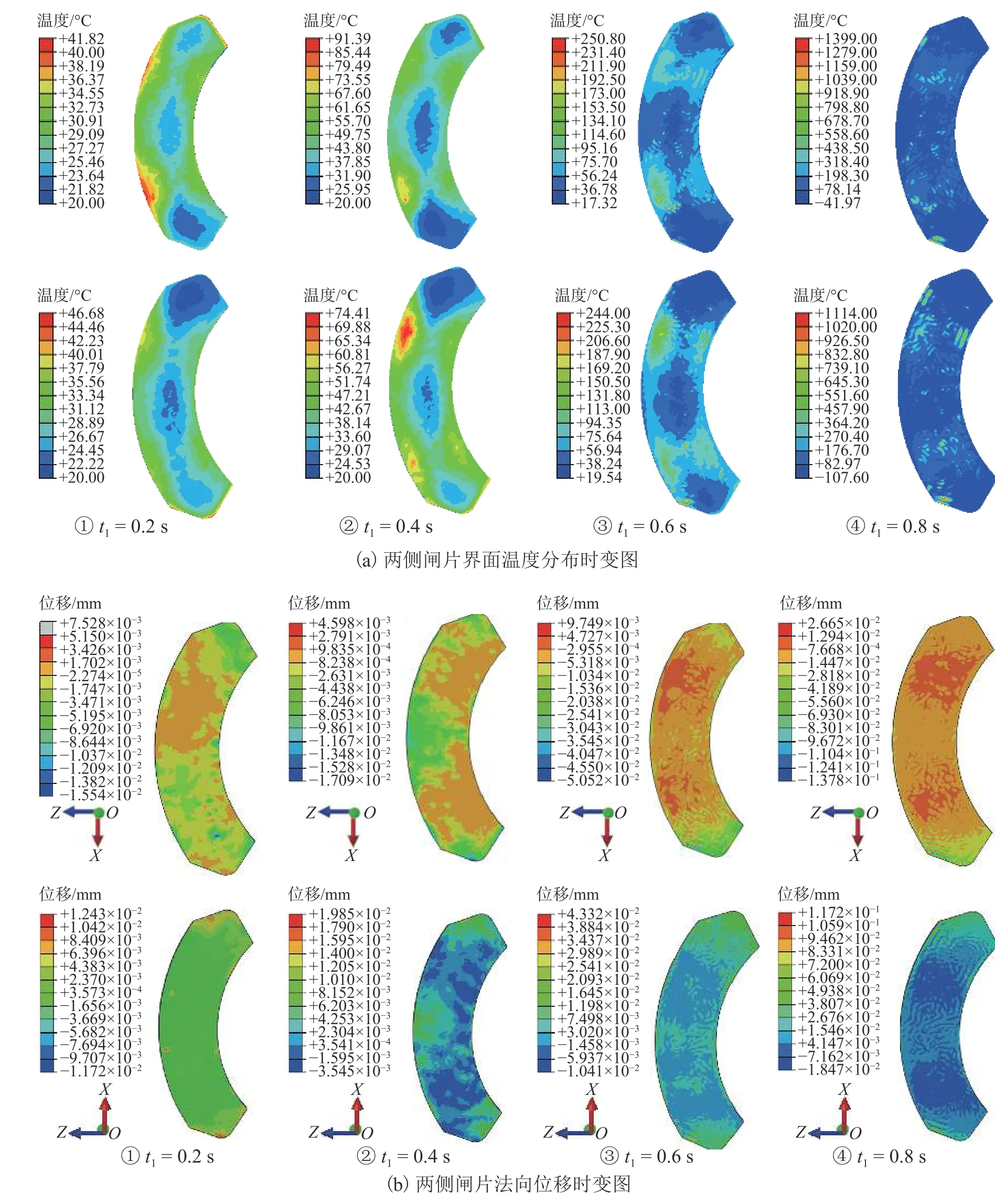
图3 两侧闸片界面温度分布与弹性变形时变图Fig. 3 Temperature distribution and normal displacement graphs of the pads in both sides

以上结果表明，制动闸片在不同的区域，周向温度分布差异显著，这主要是由于在制动摩擦过程中制动盘和闸片发生不同程度弹性翘曲变形，导致闸片和制动盘之间存在局部接触行为. 此外，可见闸片外侧周向温度明显高于中部和内侧，这是由于闸片外侧区域线速度明显高于中部和内侧区域，因此增大了摩擦副之间的发热量与热传导行为，故外侧区域周向温度更高[13]. 此外，内径区域由于接触应力更小，因此边缘区域的对流散热和热辐射效应更加明显，这进一步降低了边缘区域的温度.

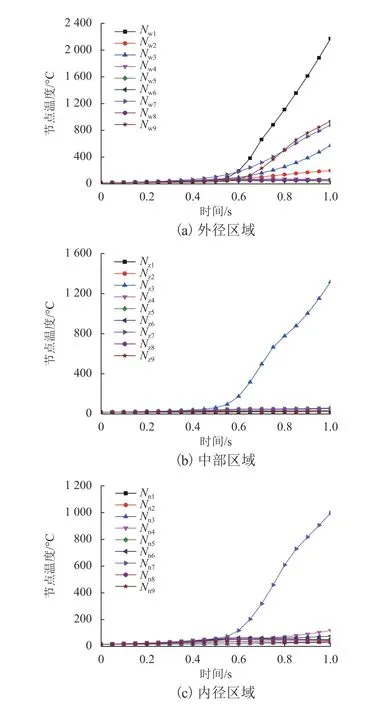
图4 闸片不同区域温度周向分布情况Fig. 4 Temperature distribution of the brake pad in circle direction

2.2.2 闸片表面径向温度分布

进一步探讨闸片表面径向温度分布特性，选取闸片表面3个区域（进摩擦区、中间区、出摩擦区）进行分析，定义径向等间距排布节点为（Nc1～Nc7，Nm1～Nm7，Nj1～Nj7），结果如图5所示. 由图5可知：闸片温度在径向区域存在明显的梯度； 在闸片出摩擦区域，闸片外径温度分布呈现制动初期上升缓慢、中后期迅速上升的趋势，节点Nc6和Nc7的温度明显高于其他节点（图5（a））；相比之下，在闸片的中间区和出摩擦区，闸片内径处呈现出明显的高温集中现象，节点Nm1、Nj1温度明显高于其他节点（图5（b）和图5（c）），这是由于摩擦副的接触状态随制动过程发生变化，从而导致闸片不同区域的径向温度分布也呈现出一定的区别.

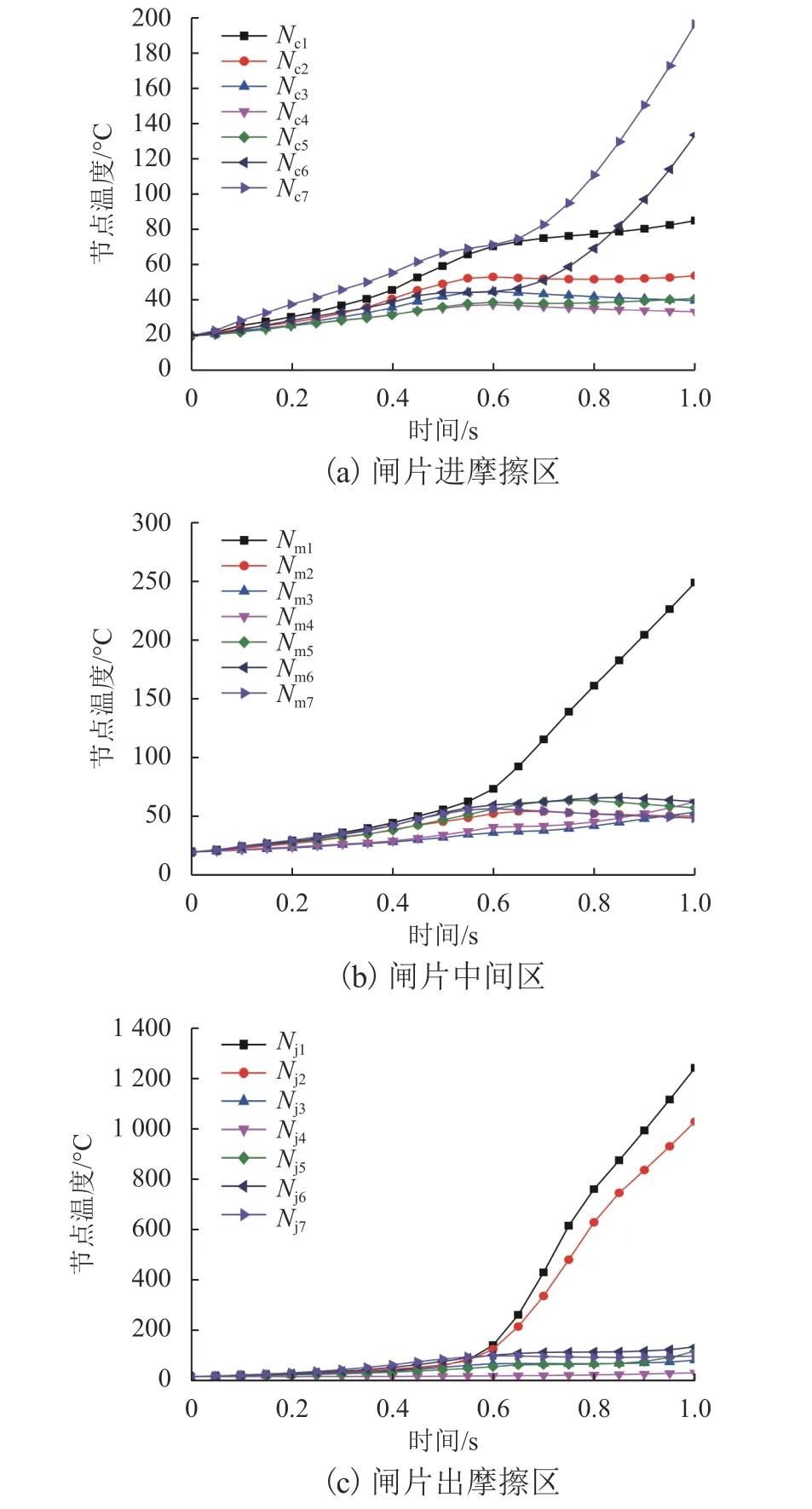
图5 闸片不同区域温度径向分布情况Fig. 5 Temperature distribution of the brake pad in radial direction

2.3 闸片表面弹性变形分析

2.3.1 闸片整体热变形分析

对热机耦合状态下闸片的整体热弹性变形行为进行分析，结果如图6所示. 由图6可见：闸片在制动前期阶段发生了明显的弹性波动，闸片的法向和切向位移均出现了较高幅度的振荡，且闸片在法向的形变相比于切向变形更加剧烈；随着制动的进行，由于制动界面整体温度升高，摩擦系数以及材料特性均发生了一定的变化，系统振动减弱，因此闸片在两个方向上的振荡程度明显减弱，但是依然可见闸片的变形量呈逐渐增大的趋势，位移形变量达到0.006 mm，这是由于界面温度在制动过程中始终处于增大的状态，相应的热弹性变形也呈现类似的趋势.

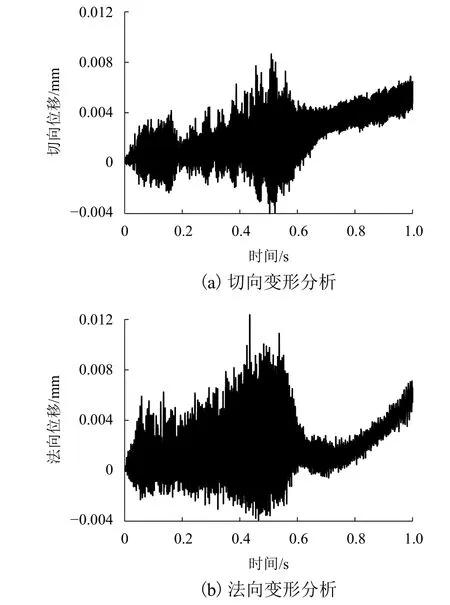
图6 闸片在法向和切向热弹性变形行为Fig. 6 Deformation of the brake pad in both the tangential and normal directions

2.3.2 闸片表面周向弹性变形分析

为探究闸片接触表面的热弹性变形行为，对闸片与制动盘接触表面上节点（中间区域Nz1～Nz9）的法向位移进行分析. 首先分析热弹性变形的周向分布特性，如图7所示. 由图7可以看出：随着制动的进行，热变形主要发生在闸片的头部和尾部上（出摩擦区和进摩擦区），其中闸片在出摩擦区的变形量（35 μm）明显大于进摩擦区处（25 μm），这是由于制动盘在进出摩擦区的热翘曲量不同，且翘曲量在初期增加较慢、中后期增长迅速，这是受摩擦片进摩擦区初期升温慢、中后期升温迅速所影响的； 此外，闸片的中部呈现出明显的“凹陷”的现象，即随着制动的进行，闸片中部区域没有出现明显的热弹性变形，这是由于热翘曲变形使得闸片和制动盘在中部区域没有形成良好的接触，导致对流换热明显，界面温度升高较少，因此中间区域没有形成明显的热弹性变形. 以上结果也与图4所示的结果一致，即周向高温区主要集中在闸片的两侧，而中间区域没有形成高温区.

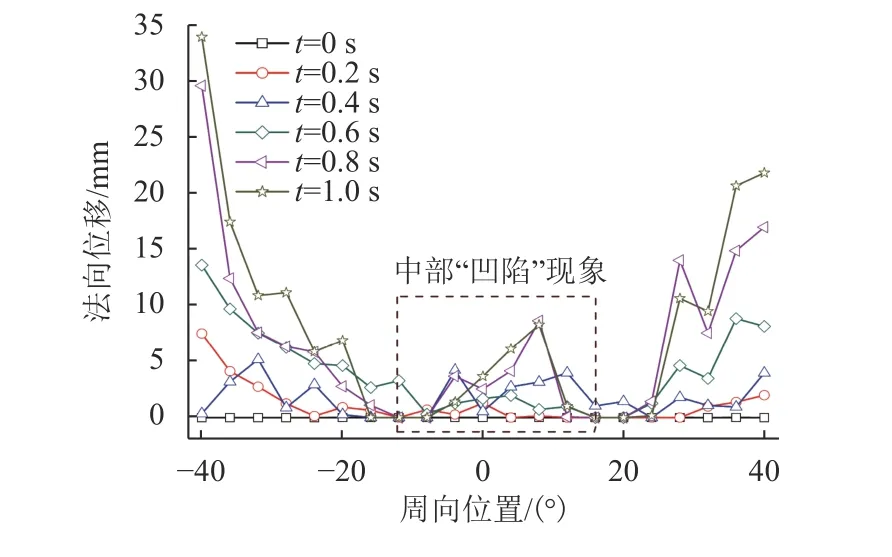
图7 闸片弹性变形周向分布Fig. 7 Elastic deformation of the pad in circular direction

2.3.3 闸片表面径向弹性变形分析

进一步地，求解闸片弹性变形法向分布的时变特性（中间区域Nm1～Nm7），如图8所示. 由图8可见：闸片法向位移在制动初期阶段呈现出锯齿状，该形状的波动来源于制动界面接触压力变化和温度变化效应的影响，正好对应初始阶段制动系统处于高频振荡的状态；随时间不断增长，法向位移呈现逐渐增大的趋势，尤其是在节点Nm3（近闸片外径处），其法向位移显著增加至0.02 mm，这也是受制动盘总体热翘曲的影响，使得局部区域变形严重.

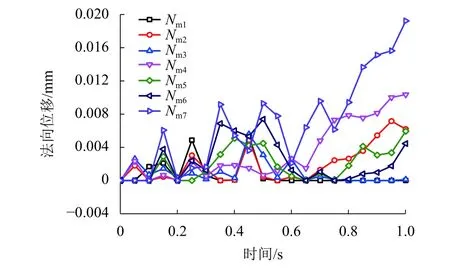
图8 闸片弹性变形径向分布Fig. 8 Elastic deformation of the pad in radial direction

2.4 制动系统动力学行为分析

2.4.1 系统振动信号分析

为了进一步说明热机耦合作用对制动系统动力学行为的影响，研究对比分析在有/无热机耦合作用下的制动系统振动信号，结果如图9（a）、（b）所示.由图9（a）、（b）可见：当忽略热机耦合作用时，系统振动信号和界面摩擦力信号呈现出较为连续的波动，这说明制动系统发生了持续的自激振动，并可能产生尖叫噪声；相反的是，当热机耦合作用存在时，制动系统仅在制动的一定阶段内出现了明显的自激振动，而随着制动摩擦的进行，系统的振动强度逐步降低，系统趋于稳定. 这是由于界面摩擦系数随着温度的升高逐渐降低[14]，从而降低了系统的振动倾向.值得注意的是，在系统考虑热机耦合时，其自激振动阶段的振动强度相比于无热机耦合状态下更大，这是由于温度升高导致摩擦副之间的接触刚度发生变化，在一定接触刚度状态下系统有可能出现强度更大的振动现象.

进一步对两种状态下的振动信号进行FFT（快速傅里叶变换）分析，结果如图9（c）所示. 由图9（c）可见：系统的振动主频并不会因为热机耦合的做用发生明显的变化，这主要是由于制动系统不稳定振动现象通常是由于系统模态耦合特性造成的，它通常取决于系统的结构特性，而受到热力学影响相对较小；但是系统振动主频处的能量在考虑热机耦合的情况下明显上升，从105 dB增大至113 dB，这也说明了热机耦合状态下制动系统自激振动强度增大.

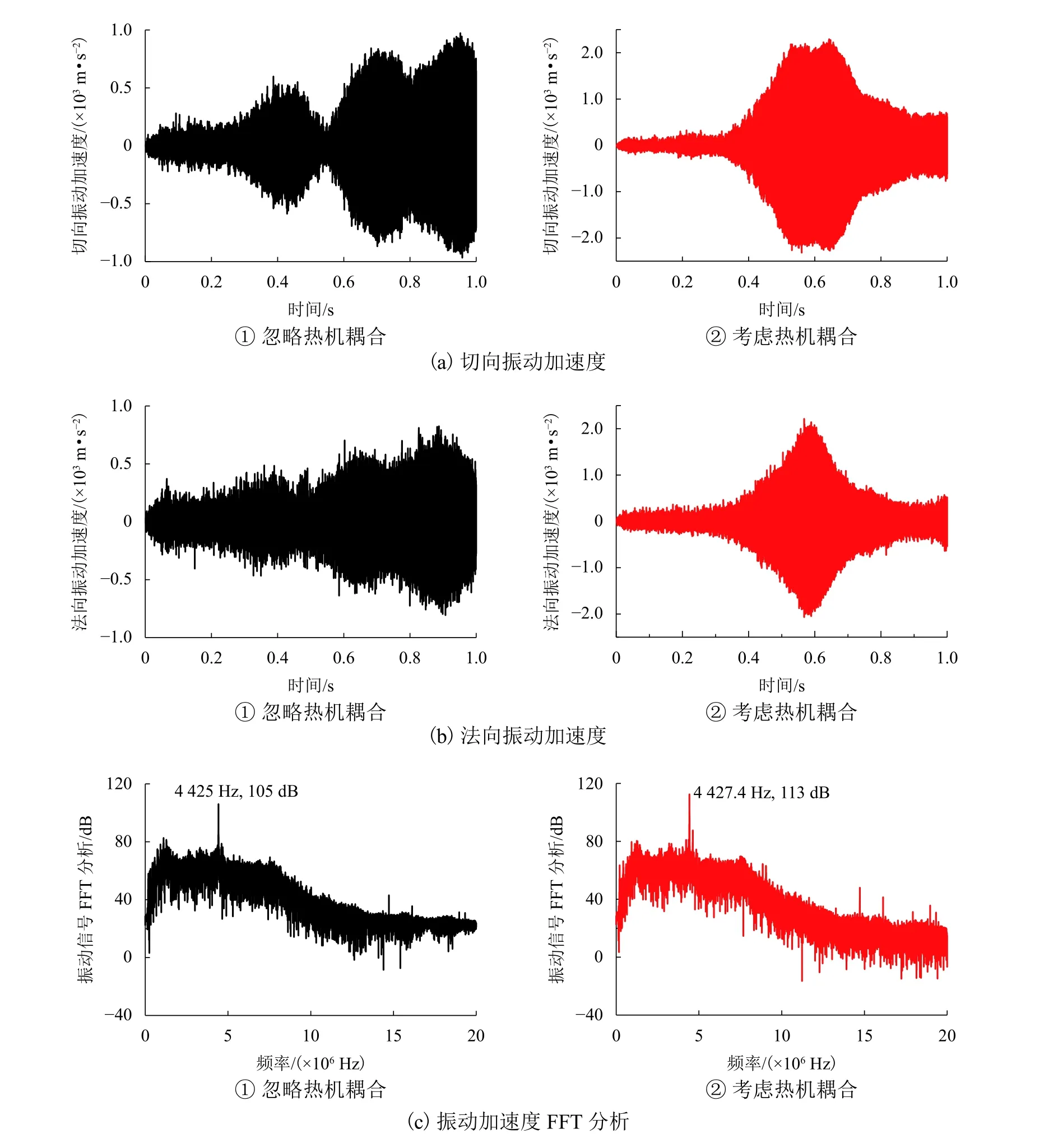
图9 列车制动系统振动信号分析Fig. 9 Vibration signals analysis of the high speed train disc brake system

2.4.2 系统接触应力分析

热机耦合特性对列车制动界面的接触法向力和摩擦力具有重要影响，图10为制动系统在忽略/考虑热机耦合作用下，界面法向力和摩擦力随制动时间变化曲线. 由图10可以看出：在忽略热机耦合作用下，制动界面法向力和切向力均出现了明显的持续振荡，且该振荡以较稳定的幅值一直持续到计算结束；相比之下，当考虑热机耦合作用时，在0～0.6 s时间内，界面法向力出现了持续的高幅度波动，相应的摩擦力也呈现出明显的波动现象；随着制动过程的进行，由于界面温度升高，制动部件发生了不同程度的翘曲变形，这导致界面法向力呈现出一定程度的上升，但是由于摩擦系数的降低和材料的软化，可见界面力信号的波动程度逐渐减弱[15]. 以上结果也说明了在热机耦合状态下，界面力有一定程度的增大，但是力信号的波动程度有所降低，这也与Ouyang等[13]在对汽车制动系统热机耦合行为的研究中得到的结论一致.

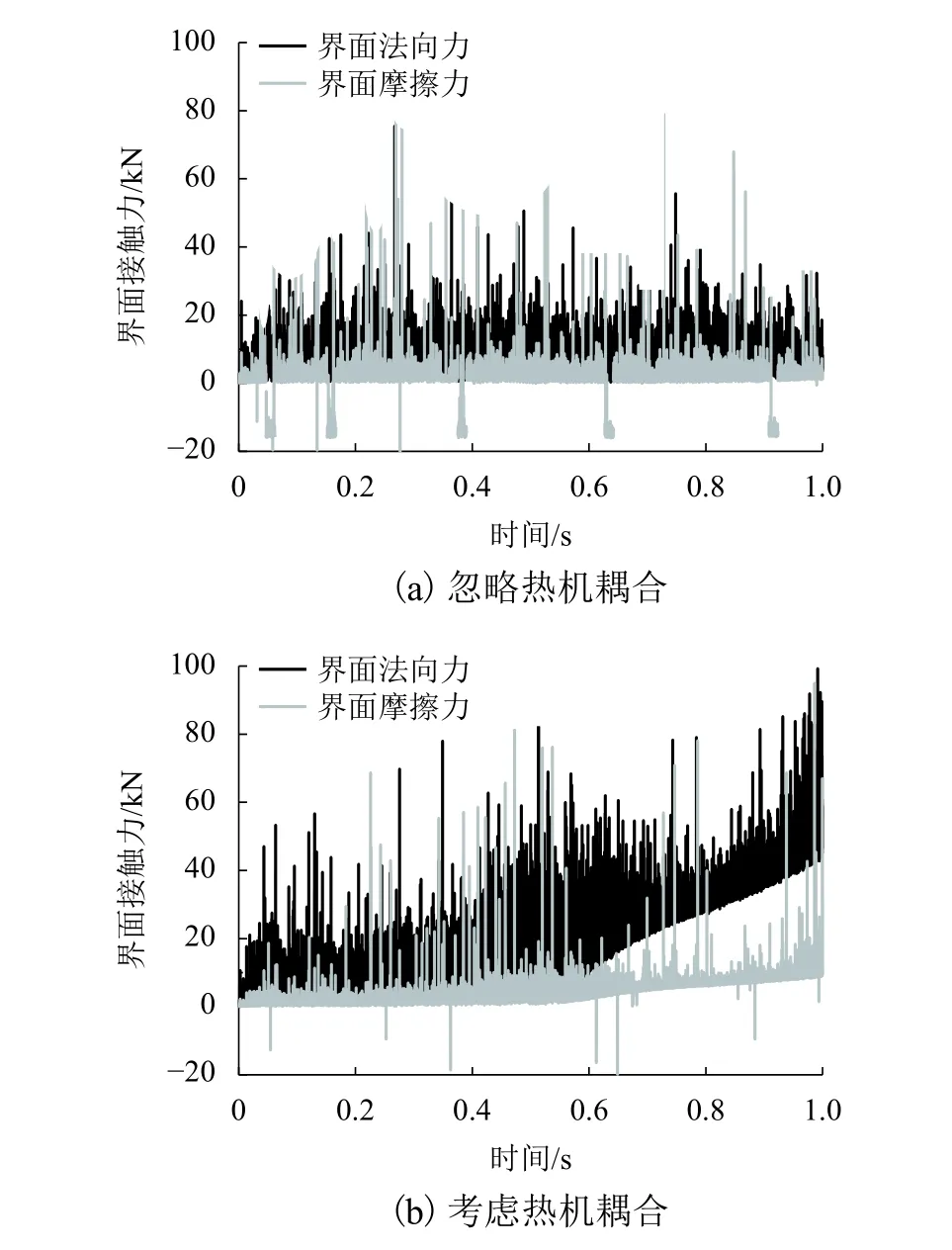
图10 界面法向力和摩擦力Fig. 10 Normal force and friction force of the brake system

3 结 论

1） 制动过程中，闸片表面温度处于动态变化的过程，高温区从闸片的进摩擦区逐渐向中部和出摩擦区流动，且闸片表面的局部区域会形成持久的高温区，导致热斑产生.

2） 由于制动盘和闸片发生一定程度弹性翘曲变形，因此闸片的周向温度分布和径向温度分布出现复杂的特性，且在闸片的内外径处和进/出摩擦区域的温度分布差异显著.

3） 热变形主要发生在闸片的两侧，闸片在进摩擦区的变形量明显大于出摩擦区处，而闸片中部区域没有出现明显的热变形现象.

4） 热机耦合作用下制动系统振动经历先增大后降低的过程，整体强度相比于忽略热机耦合的情况下更大，对应主频处的振动能量也有所上升. 此外，在热机耦合状态下，界面接触力波动程度先增大后降低且总体呈上升趋势.